2.3.3直线与平面垂直的性质(共21张PPT)
文档属性
| 名称 | 2.3.3直线与平面垂直的性质(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 16:01:34 | ||
图片预览





文档简介
(共21张PPT)
2.3.3 直线与平面垂直的性质
新课导入
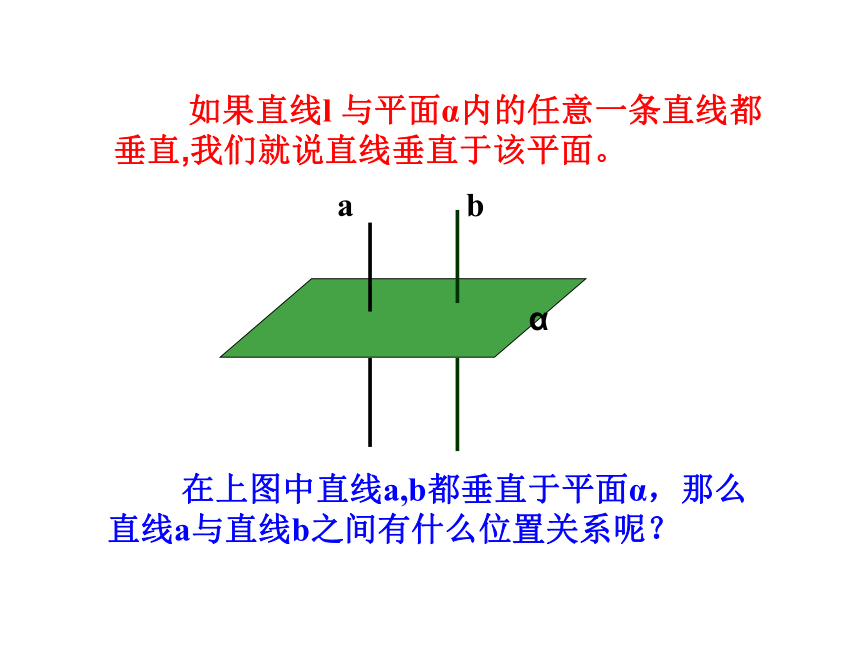
如果直线l 与平面α内的任意一条直线都垂直,我们就说直线垂直于该平面。
在上图中直线a,b都垂直于平面α,那么直线a与直线b之间有什么位置关系呢?
a
b
α
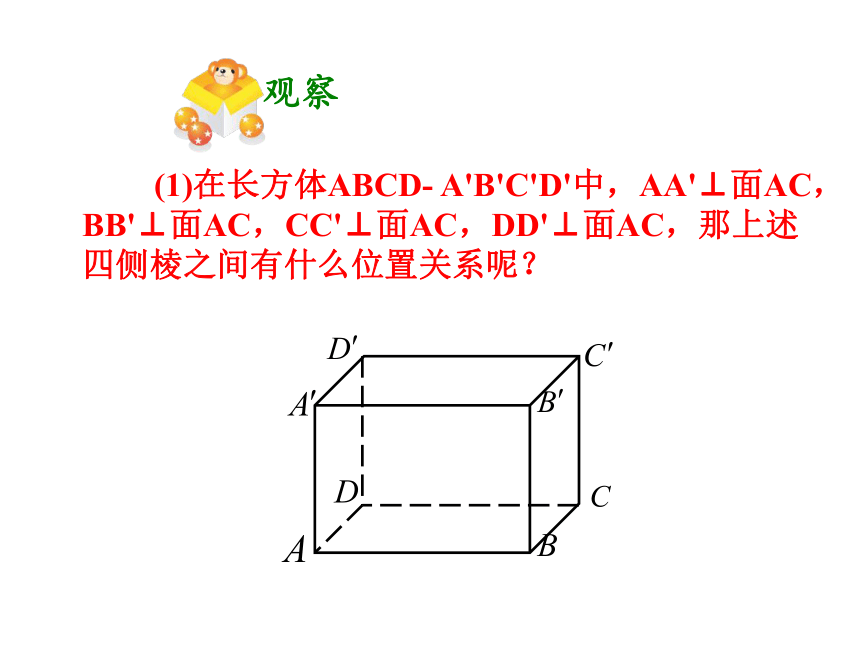
(1)在长方体ABCD- A'B'C'D'中,AA'⊥面AC,BB'⊥面AC,CC'⊥面AC,DD'⊥面AC,那上述四侧棱之间有什么位置关系呢?
观察
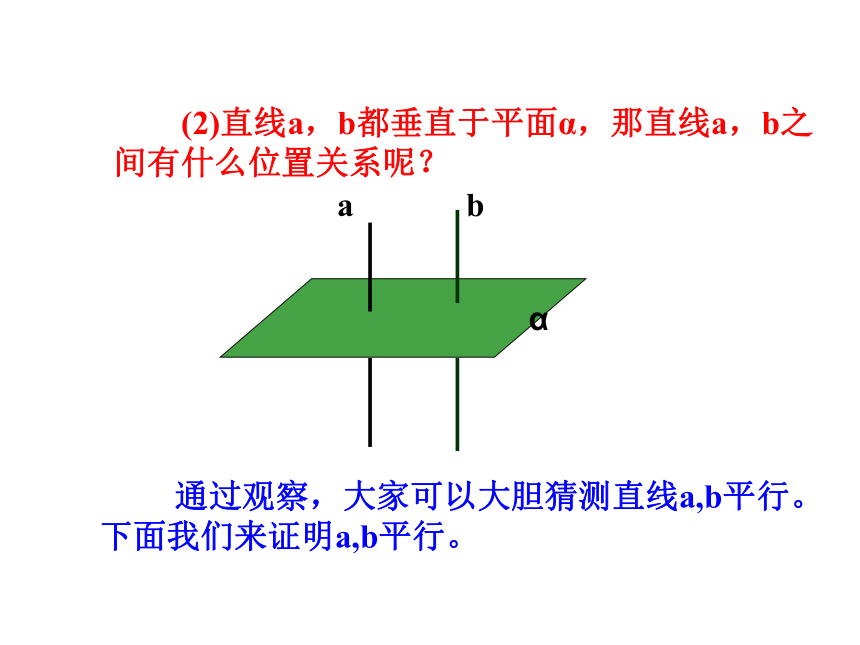
a
b
α
(2)直线a,b都垂直于平面α,那直线a,b之间有什么位置关系呢?
通过观察,大家可以大胆猜测直线a,b平行。下面我们来证明a,b平行。
O
b’
证明:(反证法)
假设a与b不平行
∵b⊥ ,设求b∩ =O,过点O做b'// ,
∵a⊥ ,∴b'⊥
则过一点O有两条直线b与b'⊥
这与过一点有且只有一条直线与已知平面垂直矛盾。
故假设不成立。
∴a//b
a
b
α
已知a⊥ ,b⊥ ,求证a//b。
直线和平面垂直的性质定理
符号表示:
垂直于同一平面的两直线互相平行。
线面垂直
线线平行
a
b
α
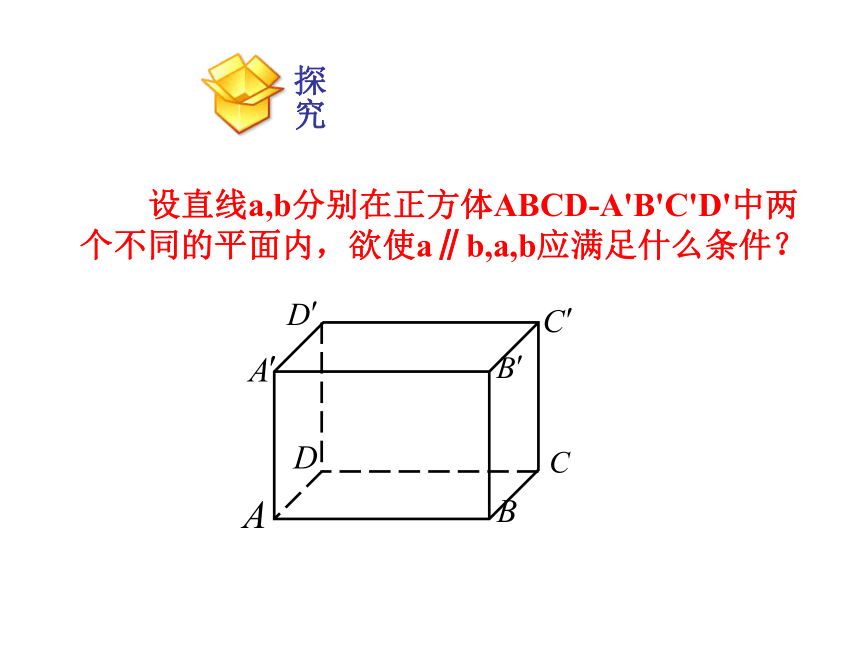
设直线a,b分别在正方体ABCD-A'B'C'D'中两个不同的平面内,欲使a∥b,a,b应满足什么条件?
探究
若a,b分别在正方体的两个相对面内,此时直线a,b必为这两个必为这两个面与第三个平面的交线。
a
b
若a,b分别在正方体的两个相邻面内,此时直线a,b必与这两个面的交线平行。
a
b
A
B
C
α
β
l
a
例六
如图,已知α∩β=l,CA⊥ 于点A,CB⊥β于点B,a ,a⊥AB,求证:a//l。
证明:
∵CA⊥面 ,∴CA ⊥a,
又∵a⊥ AB,∴ a⊥面ABC
∵CA⊥面 ∴CA ⊥ l,
同理CB⊥ l,
∴l⊥面ABC
∴a//l。
a
b
l
A
B
c
例七
已知l⊥α,l⊥β,求证α//β。
课堂小结
直线和平面垂直的性质定理:(用来判断两直线平行)
垂直于同一平面的两直线互相平行。
a
b
α
高考链接
1.(2019 广东,14分)如图,已知正方形
的棱长为2,点E是正方形
的中心,点F,G分别是棱 , 的中点。设点
分别是点E,G在平面 内的正投影。
(Ⅰ)求以E为顶点,以四边形FGAR在平面
内的正投影为底面边界的棱锥的体积;
(Ⅱ)证明 ⊥平面 ;
(Ⅲ)求异面直线 与EA所成角的正弦值。
。
。
随堂练习
2)在空间中,垂直于同一直线的两条直线互相平行( )
3)垂直于同一平面的两直线互相平行( )
1)在平面中,垂直于同一直线的两条直线互相平行( )
4)垂直于同一直线的两平面互相平行( )
×
√
√
√
1.判断
2.如图,已知
求证:
α
a
A
B
b
β
l
提示:做b的平行线交a于点A,交α于点B,由直线a和AB做平面β,易知AB⊥两面交线,又由AB⊥a,得出a//两面交线,进而a//α。
(2)若∠PDA=45°,求证:MN⊥面PCD
3.如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点求证:(1)MN⊥CD,
P
A
B
C
D
M
N
E
E
A
B
C
D
2.3.3 直线与平面垂直的性质
新课导入
如果直线l 与平面α内的任意一条直线都垂直,我们就说直线垂直于该平面。
在上图中直线a,b都垂直于平面α,那么直线a与直线b之间有什么位置关系呢?
a
b
α
(1)在长方体ABCD- A'B'C'D'中,AA'⊥面AC,BB'⊥面AC,CC'⊥面AC,DD'⊥面AC,那上述四侧棱之间有什么位置关系呢?
观察
a
b
α
(2)直线a,b都垂直于平面α,那直线a,b之间有什么位置关系呢?
通过观察,大家可以大胆猜测直线a,b平行。下面我们来证明a,b平行。
O
b’
证明:(反证法)
假设a与b不平行
∵b⊥ ,设求b∩ =O,过点O做b'// ,
∵a⊥ ,∴b'⊥
则过一点O有两条直线b与b'⊥
这与过一点有且只有一条直线与已知平面垂直矛盾。
故假设不成立。
∴a//b
a
b
α
已知a⊥ ,b⊥ ,求证a//b。
直线和平面垂直的性质定理
符号表示:
垂直于同一平面的两直线互相平行。
线面垂直
线线平行
a
b
α
设直线a,b分别在正方体ABCD-A'B'C'D'中两个不同的平面内,欲使a∥b,a,b应满足什么条件?
探究
若a,b分别在正方体的两个相对面内,此时直线a,b必为这两个必为这两个面与第三个平面的交线。
a
b
若a,b分别在正方体的两个相邻面内,此时直线a,b必与这两个面的交线平行。
a
b
A
B
C
α
β
l
a
例六
如图,已知α∩β=l,CA⊥ 于点A,CB⊥β于点B,a ,a⊥AB,求证:a//l。
证明:
∵CA⊥面 ,∴CA ⊥a,
又∵a⊥ AB,∴ a⊥面ABC
∵CA⊥面 ∴CA ⊥ l,
同理CB⊥ l,
∴l⊥面ABC
∴a//l。
a
b
l
A
B
c
例七
已知l⊥α,l⊥β,求证α//β。
课堂小结
直线和平面垂直的性质定理:(用来判断两直线平行)
垂直于同一平面的两直线互相平行。
a
b
α
高考链接
1.(2019 广东,14分)如图,已知正方形
的棱长为2,点E是正方形
的中心,点F,G分别是棱 , 的中点。设点
分别是点E,G在平面 内的正投影。
(Ⅰ)求以E为顶点,以四边形FGAR在平面
内的正投影为底面边界的棱锥的体积;
(Ⅱ)证明 ⊥平面 ;
(Ⅲ)求异面直线 与EA所成角的正弦值。
。
。
随堂练习
2)在空间中,垂直于同一直线的两条直线互相平行( )
3)垂直于同一平面的两直线互相平行( )
1)在平面中,垂直于同一直线的两条直线互相平行( )
4)垂直于同一直线的两平面互相平行( )
×
√
√
√
1.判断
2.如图,已知
求证:
α
a
A
B
b
β
l
提示:做b的平行线交a于点A,交α于点B,由直线a和AB做平面β,易知AB⊥两面交线,又由AB⊥a,得出a//两面交线,进而a//α。
(2)若∠PDA=45°,求证:MN⊥面PCD
3.如图,已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点求证:(1)MN⊥CD,
P
A
B
C
D
M
N
E
E
A
B
C
D
