2.3.4平面与平面垂直的性质(共24张PPT)
文档属性
| 名称 | 2.3.4平面与平面垂直的性质(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 818.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
2.3.4 平面与平面垂直的性质
新课导入
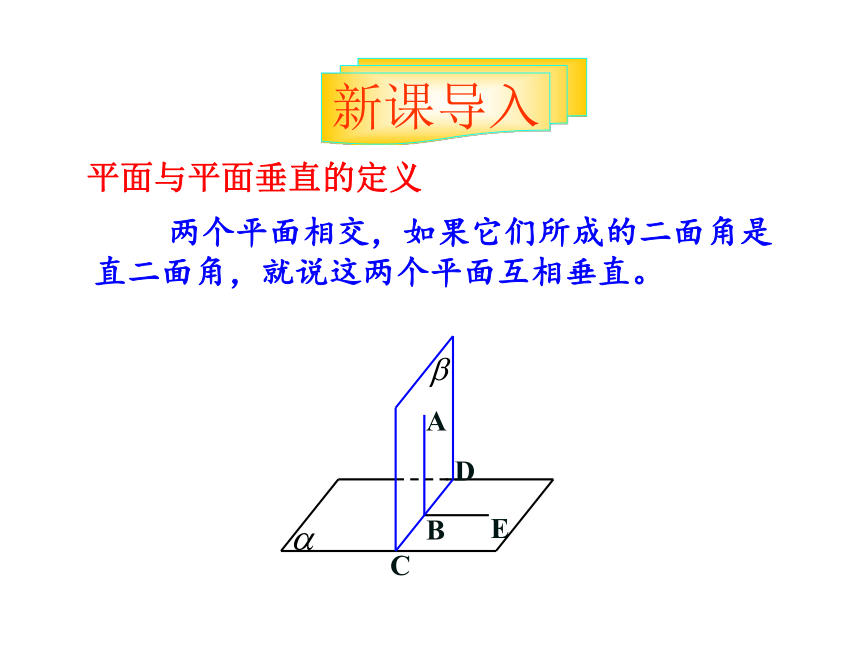
平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
E
D
C
A
B
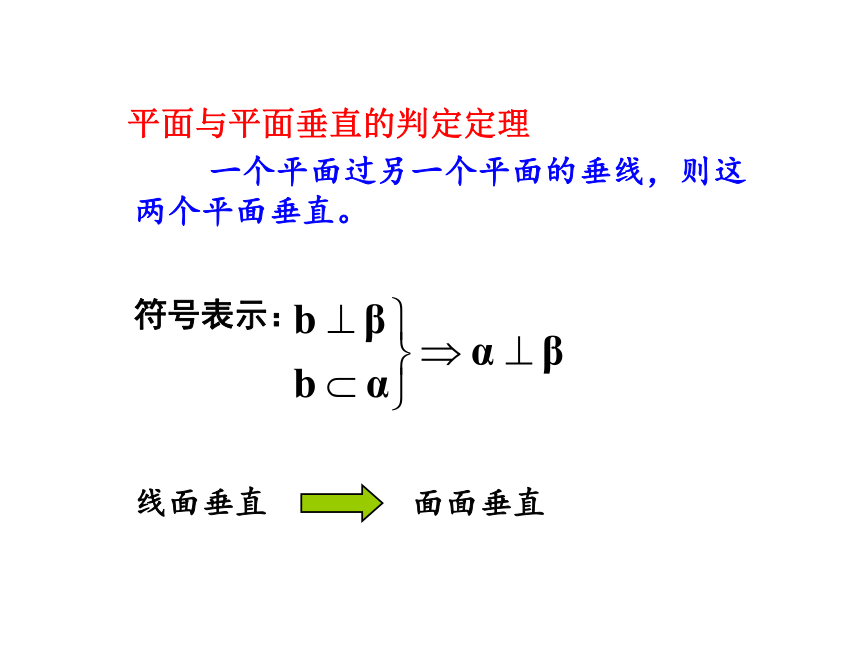
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
符号表示:
面面垂直
线面垂直
(1)如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
l
l
α
β
思考
α
β
α
β
l
(2)观察黑板所在的平面和地面,它们是互相垂直的,那么黑板所在的平面里的任意一条直线是否就一定和地面垂直?
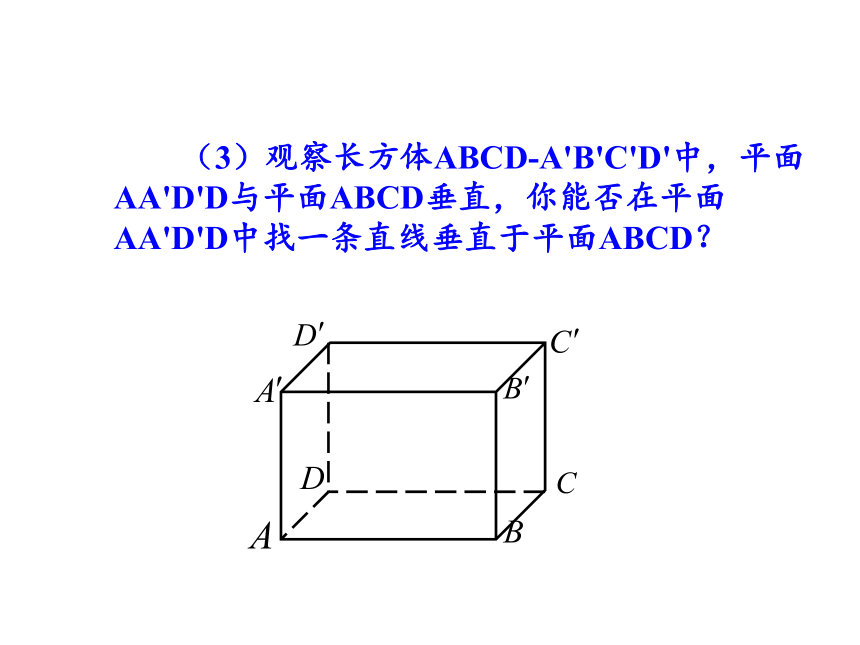
(3)观察长方体ABCD-A'B'C'D'中,平面AA'D'D与平面ABCD垂直,你能否在平面AA'D'D中找一条直线垂直于平面ABCD?
(4)如何从面β中找出一条直线,令其垂直于面α?在β内做直线BO⊥l,l垂直于平面α吗?
O
B
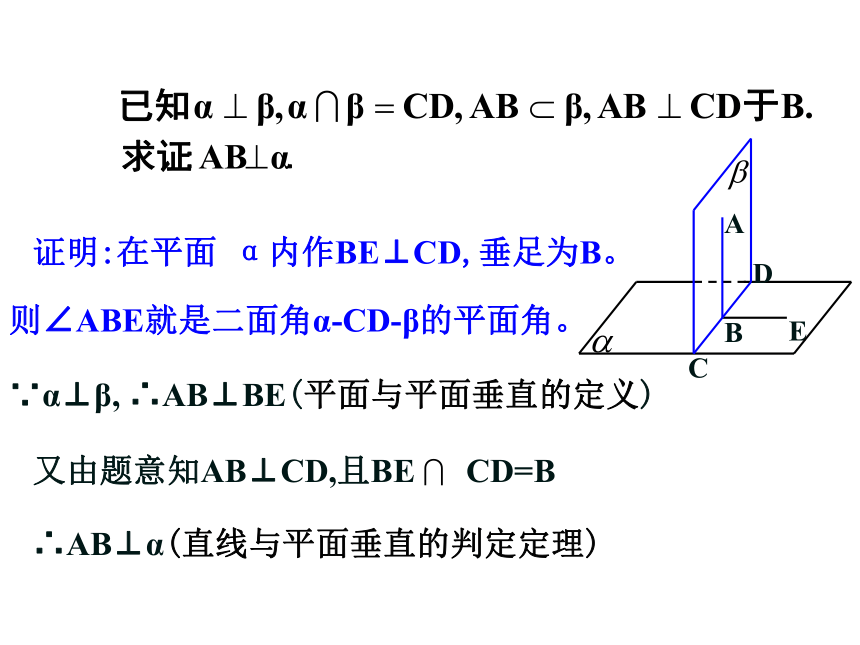
下面,我们来证明l⊥α
则∠ABE就是二面角α-CD-β的平面角。
∵α⊥β, ∴AB⊥BE(平面与平面垂直的定义)
又由题意知AB⊥CD,且BE CD=B
E
证明:在平面 α内作BE⊥CD,垂足为B。
∴AB⊥α(直线与平面垂直的判定定理)
D
C
A
B
平面和平面垂直的性质定理
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
A
O
B
符号表示:
面面垂直
线面垂直
α
β
P
C
A
平面?⊥平面β,点P在平面?内,过点P作平面β的垂线PC,直线PC与平面?具有什么位置关系?
思考
猜想:直线PC在平面?内
B
已知:?⊥β,?∩β=AB, P∈ ?,PC ⊥ β.求证:PC ?。
α
β
P
C
A
B
D
过P做PD⊥AB,垂足为D。
∵PD⊥AB,∴PD⊥面β。
∵过一点只能做一条直线与平面垂直。
∴PC与PD必重合,即PC在面α内。
解:在 内作垂直于 与β交线的直线b。
又∵a
∵
∴b ⊥β(平面与平面垂直的性质定理)
∵ ⊥β
∴a//b(直线与平面垂直的性质定理)
∴a// (直线与平面平行的判定定理)
即直线a与平面 平行。
例八
如图:已知平面α,β, ⊥β,直线a满足 a⊥β,a ,判断直线a与平面 的位置关系。
⊥β
AB是⊙O的直径,点C是圆上异于A,B的任意一点,PA⊥平面ABC,AF⊥PC于F.求证:AF⊥平面PBC。
A
C
B
O
P
F
.
证明: ∵AB是⊙O的直径
∴AC⊥CB
∴PA⊥BC
∴BC⊥平面PAC
∴平面PBC⊥平面PAC
∴AF⊥平面PBC
∵BC 平面PBC
∩
又∵AF⊥PC,AF 面PAC ,面PBC∩面PAC=PC
∩
∵PA⊥平面ABC,BC 平面ABC
∩
例九
课堂小结
证明线面垂直的两种方法:
线线垂直→线面垂直;面面垂直→线面垂直
面面垂直
线面垂直
平面和平面垂直的性质定理:
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
高考链接
1(2018 辽宁)如图,在棱长为1的正方体 中,AP=BP=b( 0(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,并求出这个值;
(Ⅲ)若与平面PQEF所成的角为45°,求与平面PQGH所成角的正弦值.
【解析】
随堂练习
1)若α⊥β,那么α内的所有直线都垂直于β( )
2)两平面互相垂直,分别在这两平面内的两直线互相垂直( )
3)两平面互相垂直,分别在两平面内且互相垂直的两直线一定分别与另一个平面垂直( )
4)两平面互相垂直,过一平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面( )
×
×
×
√
1判断
已知两个平面垂直,则:
5)一个平面内已知直线必垂直于另一个平面内的任意一条直线
6)一个平面内的已知直线必垂直于另一个平面的无数条直线
7)一个平面内的任一条直线必垂直于另一个平面
8)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面
有可能平行,相交但不垂直,异面。
可能平行,可能相交但不垂直,可能在平面内。
(×)
(√)
(×)
(√)
P
A
B
C
D
E
2.如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD。
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角。
2.3.4 平面与平面垂直的性质
新课导入
平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直。
E
D
C
A
B
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直。
符号表示:
面面垂直
线面垂直
(1)如果平面α与平面β互相垂直,直线l在平面α内,那么直线l与平面β的位置关系有哪几种可能?
l
l
α
β
思考
α
β
α
β
l
(2)观察黑板所在的平面和地面,它们是互相垂直的,那么黑板所在的平面里的任意一条直线是否就一定和地面垂直?
(3)观察长方体ABCD-A'B'C'D'中,平面AA'D'D与平面ABCD垂直,你能否在平面AA'D'D中找一条直线垂直于平面ABCD?
(4)如何从面β中找出一条直线,令其垂直于面α?在β内做直线BO⊥l,l垂直于平面α吗?
O
B
下面,我们来证明l⊥α
则∠ABE就是二面角α-CD-β的平面角。
∵α⊥β, ∴AB⊥BE(平面与平面垂直的定义)
又由题意知AB⊥CD,且BE CD=B
E
证明:在平面 α内作BE⊥CD,垂足为B。
∴AB⊥α(直线与平面垂直的判定定理)
D
C
A
B
平面和平面垂直的性质定理
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
A
O
B
符号表示:
面面垂直
线面垂直
α
β
P
C
A
平面?⊥平面β,点P在平面?内,过点P作平面β的垂线PC,直线PC与平面?具有什么位置关系?
思考
猜想:直线PC在平面?内
B
已知:?⊥β,?∩β=AB, P∈ ?,PC ⊥ β.求证:PC ?。
α
β
P
C
A
B
D
过P做PD⊥AB,垂足为D。
∵PD⊥AB,∴PD⊥面β。
∵过一点只能做一条直线与平面垂直。
∴PC与PD必重合,即PC在面α内。
解:在 内作垂直于 与β交线的直线b。
又∵a
∵
∴b ⊥β(平面与平面垂直的性质定理)
∵ ⊥β
∴a//b(直线与平面垂直的性质定理)
∴a// (直线与平面平行的判定定理)
即直线a与平面 平行。
例八
如图:已知平面α,β, ⊥β,直线a满足 a⊥β,a ,判断直线a与平面 的位置关系。
⊥β
AB是⊙O的直径,点C是圆上异于A,B的任意一点,PA⊥平面ABC,AF⊥PC于F.求证:AF⊥平面PBC。
A
C
B
O
P
F
.
证明: ∵AB是⊙O的直径
∴AC⊥CB
∴PA⊥BC
∴BC⊥平面PAC
∴平面PBC⊥平面PAC
∴AF⊥平面PBC
∵BC 平面PBC
∩
又∵AF⊥PC,AF 面PAC ,面PBC∩面PAC=PC
∩
∵PA⊥平面ABC,BC 平面ABC
∩
例九
课堂小结
证明线面垂直的两种方法:
线线垂直→线面垂直;面面垂直→线面垂直
面面垂直
线面垂直
平面和平面垂直的性质定理:
如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
高考链接
1(2018 辽宁)如图,在棱长为1的正方体 中,AP=BP=b( 0
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,并求出这个值;
(Ⅲ)若与平面PQEF所成的角为45°,求与平面PQGH所成角的正弦值.
【解析】
随堂练习
1)若α⊥β,那么α内的所有直线都垂直于β( )
2)两平面互相垂直,分别在这两平面内的两直线互相垂直( )
3)两平面互相垂直,分别在两平面内且互相垂直的两直线一定分别与另一个平面垂直( )
4)两平面互相垂直,过一平面内的任一点在该平面内作交线的垂线,则此直线必垂直与另一个平面( )
×
×
×
√
1判断
已知两个平面垂直,则:
5)一个平面内已知直线必垂直于另一个平面内的任意一条直线
6)一个平面内的已知直线必垂直于另一个平面的无数条直线
7)一个平面内的任一条直线必垂直于另一个平面
8)过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面
有可能平行,相交但不垂直,异面。
可能平行,可能相交但不垂直,可能在平面内。
(×)
(√)
(×)
(√)
P
A
B
C
D
E
2.如图,四棱锥P-ABCD的底面是矩形,AB=2, ,侧面PAB是等边三角形,且侧面PAB⊥底面ABCD。
(1)证明:侧面PAB⊥侧面PBC;
(2)求侧棱PC与底面ABCD所成的角。
