2019-2020学年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 13:21:56 | ||
图片预览

文档简介
2020年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷
一.选择题(共10小题)
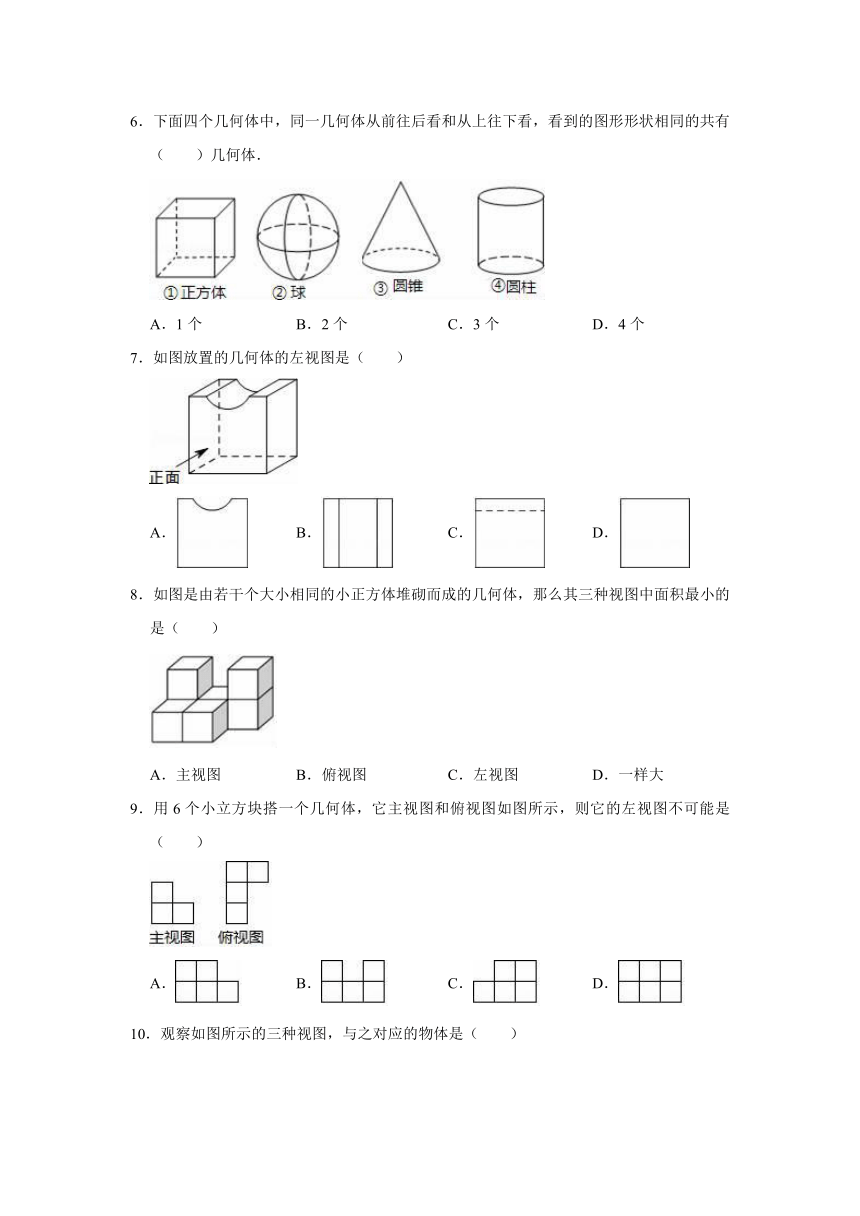
1.有一正棱锥的底面为正三角形.若此正棱锥其中两个面的周长分别为27、15,则此正棱锥所有边的长度和为多少?( )
A.36 B.42 C.45 D.48
2.如图,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH的交点P在BD上,图中面积相等的矩形有( )
A.1对 B.2对 C.3对 D.4对
3.下列四个图案中,符合如图所示的胶筒滚动后的图案是( )
A. B. C. D.
4.把正方体的六个面分别涂上白,黄,蓝,红,紫,绿六种不同的颜色,将上述大小相同,颜色分布一样的,四个正方体,拼成一个平面放置的长方体,如图所示,则正方体中与白色面相对的面的颜色是( )
A.黄色 B.蓝色 C.紫色 D.绿色
5.一个横截面为正方形的长方体,如果沿平行于横截面的方向截去长为2cm的一段后,成为一个正方体,这时侧面积减少了64cm2,则原长方体的表面积是( )
A.384cm2 B.448cm2 C.512cm2 D.640cm2
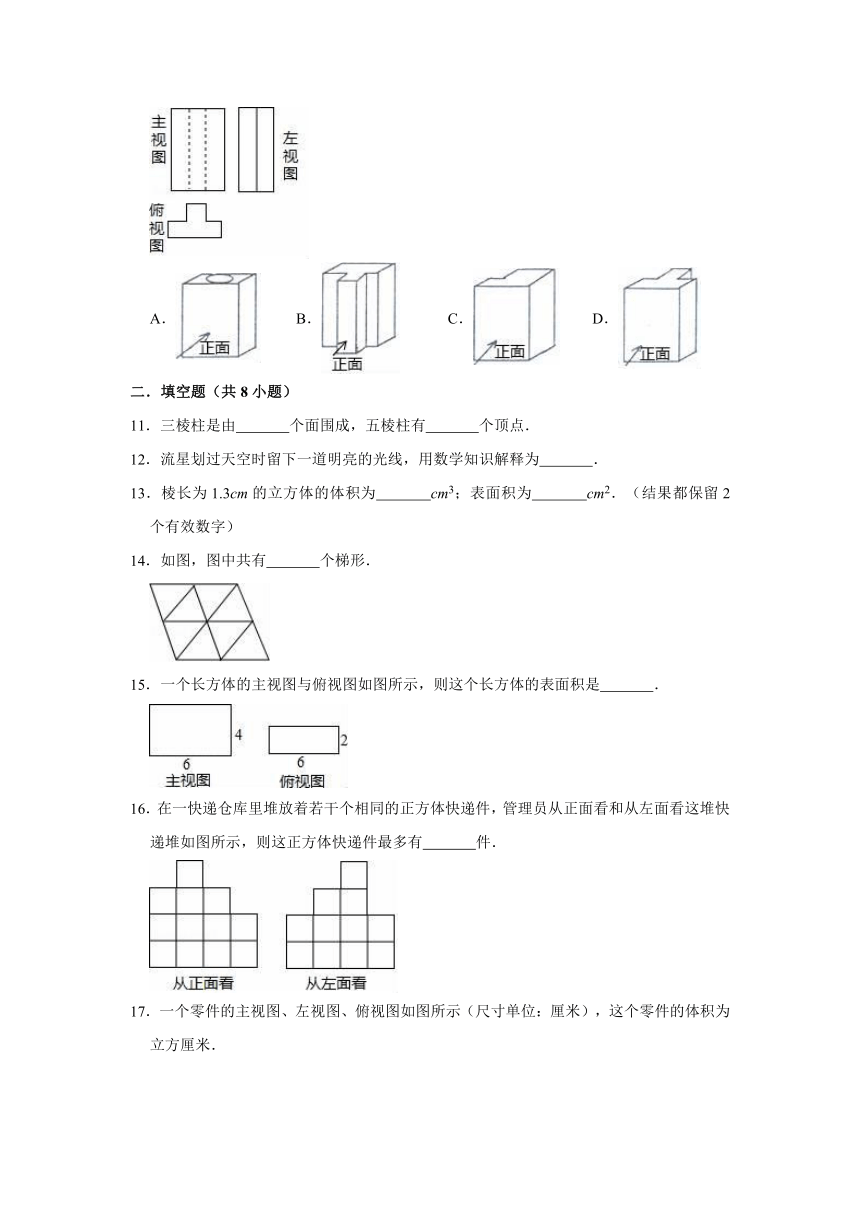
6.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
7.如图放置的几何体的左视图是( )
A. B. C. D.
8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
9.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
10.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
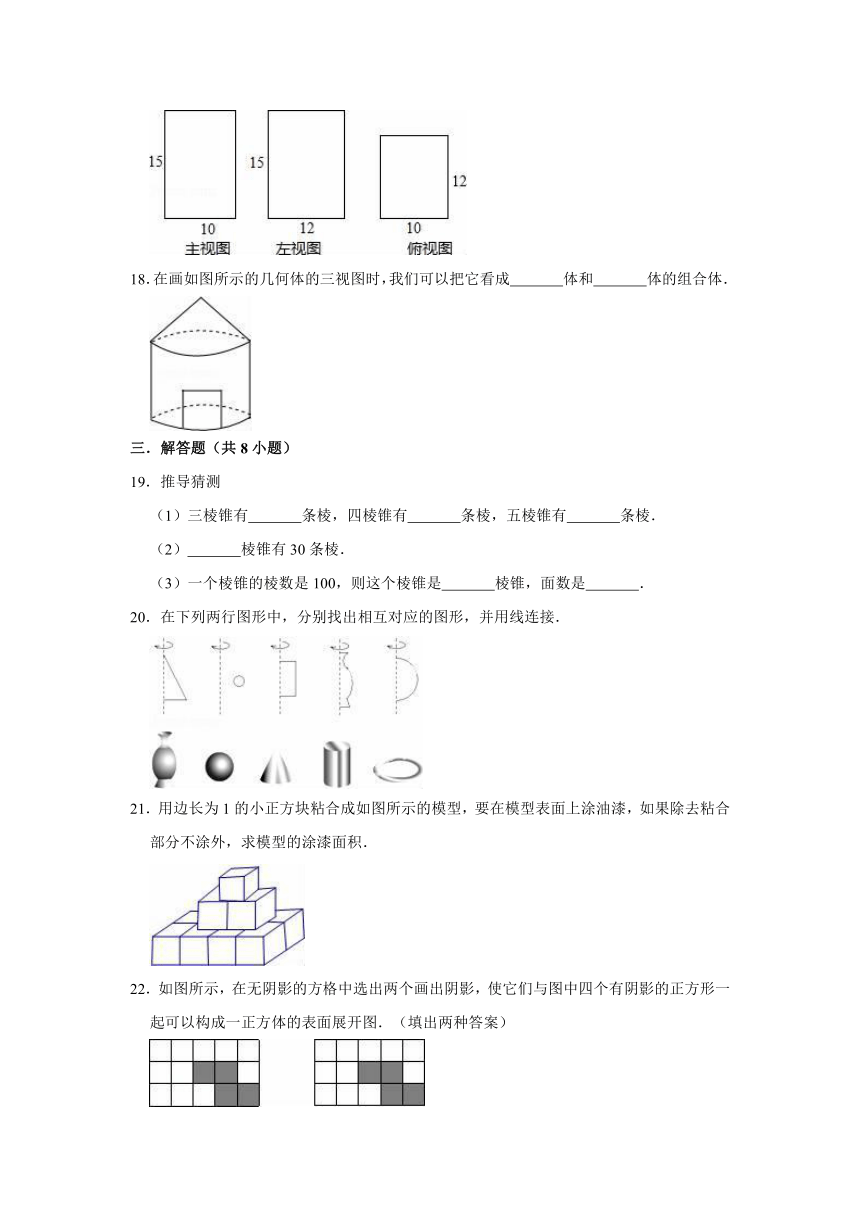
二.填空题(共8小题)
11.三棱柱是由 个面围成,五棱柱有 个顶点.
12.流星划过天空时留下一道明亮的光线,用数学知识解释为 .
13.棱长为1.3cm的立方体的体积为 cm3;表面积为 cm2.(结果都保留2个有效数字)
14.如图,图中共有 个梯形.
15.一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是 .
16.在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递堆如图所示,则这正方体快递件最多有 件.
17.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为 立方厘米.
18.在画如图所示的几何体的三视图时,我们可以把它看成 体和 体的组合体.
三.解答题(共8小题)
19.推导猜测
(1)三棱锥有 条棱,四棱锥有 条棱,五棱锥有 条棱.
(2) 棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是 棱锥,面数是 .
20.在下列两行图形中,分别找出相互对应的图形,并用线连接.
21.用边长为1的小正方块粘合成如图所示的模型,要在模型表面上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.
22.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
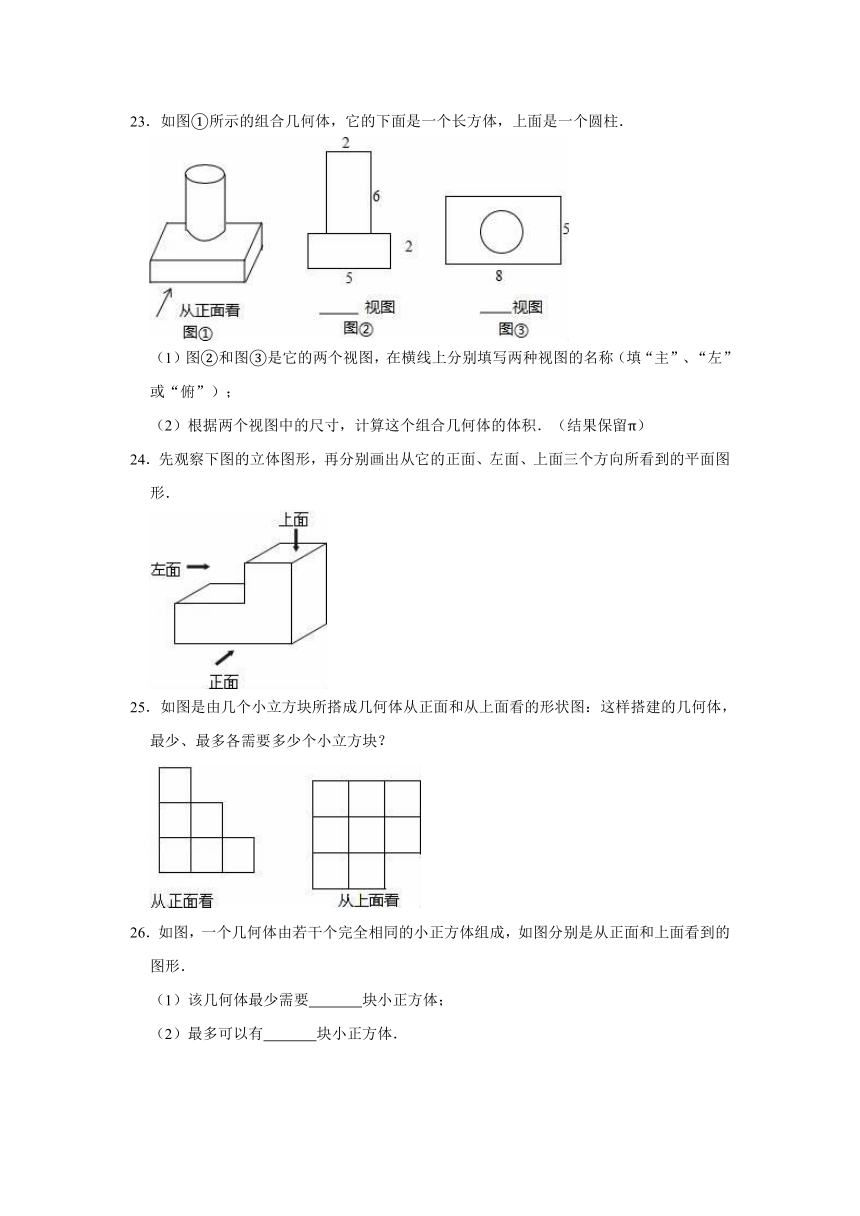
23.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
24.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
25.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
26.如图,一个几何体由若干个完全相同的小正方体组成,如图分别是从正面和上面看到的图形.
(1)该几何体最少需要 块小正方体;
(2)最多可以有 块小正方体.
2020年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.有一正棱锥的底面为正三角形.若此正棱锥其中两个面的周长分别为27、15,则此正棱锥所有边的长度和为多少?( )
A.36 B.42 C.45 D.48
【分析】根据题意画出图形,得出2y+x=27,3x=15,求出x和y,即可得出结果.
【解答】解:如图所示:根据题意得:
2y+x=27,3x=15,
其他都不符合三角形条件,解得:x=5,y=11,
∴正棱锥所有边的长度和=3x+3y=15+33=48;
故选:D.
【点评】本题考查了立体图形;根据题意画出图形,得出关系式是解决问题的关键.
2.如图,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH的交点P在BD上,图中面积相等的矩形有( )
A.1对 B.2对 C.3对 D.4对
【分析】根据矩形的性质,由全等三角形的判定得出△EPD≌△HDP,则S△EPD=S△HDP,通过对各图形的拼凑,得到的结论.
【解答】解:在矩形ABCD中,
∵EF∥AB,AB∥DC,
∴EF∥DC,则EP∥DH;故∠PED=∠DHP;
同理∠DPH=∠PDE;又PD=DP;所以△EPD≌△HDP;则S△EPD=S△HDP;
同理S△GBP=S△FPB;
则(1)S梯形BPHC=S△BDC﹣S△HDP=S△ABD﹣S△EDP=S梯形ABPE;
S?AGPE=S梯形ABPE﹣S△GBP=S梯形BPHC﹣S△FPB=S?FPHC;
(2)S?AGHD=S?AGPE+S?HDPE=S?PFCH+S?PHDE=S?EFCD;
(3)S?ABFE=S?AGPE+S?GBFP=S?PFCH+S?GBFP=S?GBCH.
故选:C.
【点评】考查了矩形的性质,本题是一道结论开放题,掌握矩形的性质,很容易得到答案.
3.下列四个图案中,符合如图所示的胶筒滚动后的图案是( )
A. B. C. D.
【分析】根据旋转的性质,找出图中三角形排列规律从左到右的方向滚涂到墙上图案即可选择答案.
【解答】解:根据旋转的性质和胶滚上的图案可知,横向状态转为正立状态,胶滚滚出的图案是.
故选:A.
【点评】本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
4.把正方体的六个面分别涂上白,黄,蓝,红,紫,绿六种不同的颜色,将上述大小相同,颜色分布一样的,四个正方体,拼成一个平面放置的长方体,如图所示,则正方体中与白色面相对的面的颜色是( )
A.黄色 B.蓝色 C.紫色 D.绿色
【分析】以“红色”为突破口,红色与紫色、黄色、白色、蓝色相邻,所以红色的对面是绿色;黄色与红色、白色、蓝色、绿色相邻,所以黄色的对面是紫色,则剩余的白色与蓝色相对.
【解答】解:最右边的正方体告诉我们:红色与蓝色、黄色相邻,中间两个正方体告诉我们:红色与紫色、白色相邻,所以红色的对面是绿色;又黄色与红色、白色、蓝色、绿色相邻,所以黄色的对面是紫色,则剩余的白色与蓝色相对.
故选:B.
【点评】此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
5.一个横截面为正方形的长方体,如果沿平行于横截面的方向截去长为2cm的一段后,成为一个正方体,这时侧面积减少了64cm2,则原长方体的表面积是( )
A.384cm2 B.448cm2 C.512cm2 D.640cm2
【分析】根据长截短2cm,就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知侧面积减少了64cm2,64÷4÷2=8cm,求出减少面的宽,也就是剩下的正方体的棱长,然后8+2=10cm求出原长方体的长,再计算原长方体的表面积即可.
【解答】解:64÷4÷2=8(cm)
8×8×6+64
=384+64
=448(cm2)
答:原来长方体的表面积是448cm2.
故选:B.
【点评】考查了几何体的表面积,根据截去后剩下是正方体,可知减少的部分是宽为2cm的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体的表面积计算方法即可求解.
6.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
【分析】根据三视图的定义、结合图形对各个几何体进行观察即可判断,得到答案.
【解答】解:正方体从前往后看和从上往下看,看到的图形形状都是正方形,①符合题意;
球从前往后看和从上往下看,看到的图形形状都是圆,②符合题意;
圆锥从前往后看和从上往下看,看到的图形形状分别是三角形和圆,③不合题意;
圆柱从前往后看和从上往下看,看到的图形形状分别是矩形和圆,④不合题意,
故选:B.
【点评】本题考查的是简单几何体的三视图,理解三视图的概念、正确观察图形是解题的关键.
7.如图放置的几何体的左视图是( )
A. B. C. D.
【分析】根据从左边看得到的图形是左视图,可得答案.
【解答】解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
【点评】本题考查了简单组合体的三视图,从左边看得到的图形是左视图,注意中间看不到的线用虚线表示.
8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故选:C.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固.解题关键是找到三种视图的正方形的个数.
9.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
【分析】由几何体的主视图和俯视图可知,该几何体的主视图的第一列3个正方形中每个正方形所在位置最多均可有2个小立方块;最少一个正方形所在位置有2个小立方块,其余2个所在位置各有1个小立方块;主视图的第二列1个小正方形所在位置只能有1个.再根据用6个小立方块搭一个几何体即可求解.
【解答】解:这样的几何体不止一种,而有多种摆法.
最少需要2+1+1+1=5(个)小立方块,最多需要2×3+1=7(个)小立方块.
因为用6个小立方块搭一个几何体,
所以它的左视图不可能是.
故选:D.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.
10.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
【分析】首先根据主视图中有两条虚线,发现该几何体的应该有两条从正面看不到的棱,然后结合俯视图及提供的三个几何体确定正确的序号.
【解答】解:结合主视图和俯视图发现几何体的背面应该有个凸起,
故淘汰选项ABC,选D.
故选:D.
【点评】本题考查了由三视图判断几何体的知识,解题的关键是结合三视图及三个几何体确定正确的答案,难度不大.
二.填空题(共8小题)
11.三棱柱是由 5 个面围成,五棱柱有 10 个顶点.
【分析】根据三棱柱、五棱柱的概念和特性即可解.
【解答】解:三棱柱有2个底面,3个侧面,共5个面围成;五棱柱有10个顶点.
故答案为:5;10.
【点评】本题考查的是认识立体图形.柱体中,面与面相交成棱,棱与棱相交成顶点.
12.流星划过天空时留下一道明亮的光线,用数学知识解释为 点动成线. .
【分析】根据点动成线进行回答.
【解答】解:流星划过天空时留下一道明亮的光线,用数学知识解释为点动成线.
故答案为:点动成线.
【点评】此题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体.
13.棱长为1.3cm的立方体的体积为 2.2 cm3;表面积为 1.7 cm2.(结果都保留2个有效数字)
【分析】根据立方体的体积V=a3,表面积S=6a2,列式计算即可求解..
【解答】解:1.33≈2.2(cm3),
1.32≈1.7(cm2).
故棱长为1.3cm的立方体的体积为2.2cm3;表面积为1.7cm2.
故答案为:2.2;1.7.
【点评】考查了几何体的体积和表面积,关键是熟悉立方体的体积V=a3,表面积S=6a2的知识点.
14.如图,图中共有 10 个梯形.
【分析】根据图形认真分析由图中可知一个梯形需一个平行四边形和一个三角形组成.
【解答】解:由图形的特点可知,一个平行四边形和一个三角形可组成一个梯形,且图形中的梯形的形状、大小相同,共有10个.
故答案为10.
【点评】有一组对边平行,另一组对边不平行的四边形是梯形.
15.一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是 88 .
【分析】根据给出的长方体的主视图和俯视图可得,长方体的长是6,宽是2,高是4,进而可根据长方体的表面积公式求出其表面积.
【解答】解:由主视图可得长方体的长为6,高为4,
由俯视图可得长方体的宽为2,
则这个长方体的表面积是
(6×2+6×4+4×2)×2
=(12+24+8)×2
=44×2
=88.
故这个长方体的表面积是88.
故答案为:88.
【点评】考查由三视图判断几何体,长方体的表面积的求法,根据长方体的主视图和俯视图得到几何体的长、宽和高是解决本题的关键.
16.在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递堆如图所示,则这正方体快递件最多有 39 件.
【分析】由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得第3层最多正方体的个数为:3×2=6;由主视图和左视图可得第4层最多正方体的个数为:1;相加可得所求.
【解答】解:由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,
最底层几何体最多正方体的个数为:4×4=16,
由主视图和左视图可得第二层最多正方体的个数为:4×4=16;
由主视图和左视图可得第3层最多正方体的个数为:3×2=6;
由主视图和左视图可得第4层最多正方体的个数为:1;
16+16+6+1=39(件).
故这正方体快递件最多有39件.
故答案为:39.
【点评】此题考查由视图判断几何体;得到最底层正方体的最多的个数是解决本题的突破点;用到的知识点为:最底层正方体的最多的个数=行数×列数.
17.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为 1800 立方厘米.
【分析】易得该几何体为长10,宽12,高15的长方体,长方体的体积=长×宽×高;
【解答】解:∵有2个视图为长方形,
∴该几何体为柱体,
∵第3个视图为长方形,
∴几何体为长方体,
∴长方体的体积为10×15×12=1800立方厘米.
故答案为:1800.
【点评】考查由视图判断几何体;用到的知识点为:有2个视图为长方形的几何体是柱体;得到该几何体长,宽,高是解决本题的突破点.
18.在画如图所示的几何体的三视图时,我们可以把它看成 圆锥 体和 圆柱 体的组合体.
【分析】由题意结合立体图形的特征可知,上部是圆锥,下部是圆柱,依此即可求解.
【解答】解:观察图形可知,在画如图所示的几何体的三视图时,我们可以把它看成圆锥体和圆柱体的组合体.
故答案为:圆锥;圆柱.
【点评】本题是基础题,考查几何体的三视图的识别能力,作图能力,三视图的投影规则是主视、俯视 长对正;主视、左视高平齐,左视、俯视宽相等.
三.解答题(共8小题)
19.推导猜测
(1)三棱锥有 6 条棱,四棱锥有 8 条棱,五棱锥有 10 条棱.
(2) 十五 棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是 五十 棱锥,面数是 51 .
【分析】(1)三棱锥侧面有3条棱,底面有3条棱,共有6条棱;四棱锥侧面有4条棱,底面有4条棱,共有8条棱;五棱锥侧面有5条棱,底面有5条棱,共有10条棱;
(2)共有30条棱,那么底面有15条棱,是十五棱锥;
(3)棱锥有100条棱,那么底面有50条棱,为五十棱锥,共有51个面.
【解答】解:(1)三棱锥有6条棱,四棱锥有8条棱,五棱锥有10条棱.
(2)十五棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是五十棱锥,面数是51.
故答案为:6,8,10;十五;五十,51.
【点评】考查了认识立体图形,关键是有规律的寻找多面体的棱及面的特点.
20.在下列两行图形中,分别找出相互对应的图形,并用线连接.
【分析】利用面动成体解答即可.
【解答】解:如图,
【点评】本题主要考查了点,线,面,体,解题的关键是培养学生的空间想象能力.
21.用边长为1的小正方块粘合成如图所示的模型,要在模型表面上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.
【分析】顶层5个面外露,5个面被涂漆;二层2个正方体外露,6个侧面和2﹣1=1个顶面,7个面被涂漆;三层8个正方体外露,12个侧面和8﹣2=6个顶面,18个面被涂漆.
【解答】解:图形中11个正方体共有面:11×6=66(个);
被涂漆面共有:5+7+18=30(个);
所以被涂漆的表面积为:30×1×1+8=38.
答:模型的涂漆面积为38.
【点评】本题考查了几何体表面积的计算,解题的关键是得出粘合部分的面积,是基础知识要熟练掌握.
22.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
【分析】根据折叠情况,即可画出图形.
【解答】解:如图所示:
【点评】本题考查了学生对几何体的展开图的理解,以及空间想象能力.
23.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体体积+上面圆柱的体积即可求解.
【解答】解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
24.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
【分析】根据图形发挥空间想象能力作出图形即可.
【解答】解:从它的正面、左面、上面三个方向所看到的平面图形(每个图(2分) )
【点评】用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.
25.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.
【解答】解:搭这样的几何体最少需要8+2+1=11个小正方体,
最多需要8+6+3=17个小正方体;
故最多需要17个小正方体,最少需要11个小正方体.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
26.如图,一个几何体由若干个完全相同的小正方体组成,如图分别是从正面和上面看到的图形.
(1)该几何体最少需要 5 块小正方体;
(2)最多可以有 6 块小正方体.
【分析】(1)由俯视图可得最底层的几何体的个数,由主视图第二层正方形的个数可得第二层最少需要几块正方体,相加即可得到该几何体最少需要几块小正方体;
(2)由俯视图和主视图可得第二层最多需要几块小正方体,再加上最底层的正方体的个数即可得到最多可以有几块小正方体.
【解答】解:俯视图中有4个正方形,那么组合几何体的最底层有4个正方体,
(1)由主视图第二层有1个正方形可得组合几何体的第二层最少有1个正方体,
所以该几何体最少需要4+1=5块小正方体;
(2)主图从上边数第一行的第二层最多可有2个正方体,
所以该几何体最多需要4+2=6块小正方体.
故答案为:5,6.
【点评】考查由三视图判断几何体;用到的知识点为:俯视图正方形的个数为组合几何体最底层的正方体的个数;左视图第二层正方形的个数为组合几何体第二层的正方体最少的个数.
一.选择题(共10小题)
1.有一正棱锥的底面为正三角形.若此正棱锥其中两个面的周长分别为27、15,则此正棱锥所有边的长度和为多少?( )
A.36 B.42 C.45 D.48
2.如图,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH的交点P在BD上,图中面积相等的矩形有( )
A.1对 B.2对 C.3对 D.4对
3.下列四个图案中,符合如图所示的胶筒滚动后的图案是( )
A. B. C. D.
4.把正方体的六个面分别涂上白,黄,蓝,红,紫,绿六种不同的颜色,将上述大小相同,颜色分布一样的,四个正方体,拼成一个平面放置的长方体,如图所示,则正方体中与白色面相对的面的颜色是( )
A.黄色 B.蓝色 C.紫色 D.绿色
5.一个横截面为正方形的长方体,如果沿平行于横截面的方向截去长为2cm的一段后,成为一个正方体,这时侧面积减少了64cm2,则原长方体的表面积是( )
A.384cm2 B.448cm2 C.512cm2 D.640cm2
6.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
7.如图放置的几何体的左视图是( )
A. B. C. D.
8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
9.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
10.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
二.填空题(共8小题)
11.三棱柱是由 个面围成,五棱柱有 个顶点.
12.流星划过天空时留下一道明亮的光线,用数学知识解释为 .
13.棱长为1.3cm的立方体的体积为 cm3;表面积为 cm2.(结果都保留2个有效数字)
14.如图,图中共有 个梯形.
15.一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是 .
16.在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递堆如图所示,则这正方体快递件最多有 件.
17.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为 立方厘米.
18.在画如图所示的几何体的三视图时,我们可以把它看成 体和 体的组合体.
三.解答题(共8小题)
19.推导猜测
(1)三棱锥有 条棱,四棱锥有 条棱,五棱锥有 条棱.
(2) 棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是 棱锥,面数是 .
20.在下列两行图形中,分别找出相互对应的图形,并用线连接.
21.用边长为1的小正方块粘合成如图所示的模型,要在模型表面上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.
22.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
23.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
24.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
25.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
26.如图,一个几何体由若干个完全相同的小正方体组成,如图分别是从正面和上面看到的图形.
(1)该几何体最少需要 块小正方体;
(2)最多可以有 块小正方体.
2020年苏科新版七年级上册数学《第5章 走进图形世界》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.有一正棱锥的底面为正三角形.若此正棱锥其中两个面的周长分别为27、15,则此正棱锥所有边的长度和为多少?( )
A.36 B.42 C.45 D.48
【分析】根据题意画出图形,得出2y+x=27,3x=15,求出x和y,即可得出结果.
【解答】解:如图所示:根据题意得:
2y+x=27,3x=15,
其他都不符合三角形条件,解得:x=5,y=11,
∴正棱锥所有边的长度和=3x+3y=15+33=48;
故选:D.
【点评】本题考查了立体图形;根据题意画出图形,得出关系式是解决问题的关键.
2.如图,在矩形ABCD中,EF∥AB,GH∥BC,EF、GH的交点P在BD上,图中面积相等的矩形有( )
A.1对 B.2对 C.3对 D.4对
【分析】根据矩形的性质,由全等三角形的判定得出△EPD≌△HDP,则S△EPD=S△HDP,通过对各图形的拼凑,得到的结论.
【解答】解:在矩形ABCD中,
∵EF∥AB,AB∥DC,
∴EF∥DC,则EP∥DH;故∠PED=∠DHP;
同理∠DPH=∠PDE;又PD=DP;所以△EPD≌△HDP;则S△EPD=S△HDP;
同理S△GBP=S△FPB;
则(1)S梯形BPHC=S△BDC﹣S△HDP=S△ABD﹣S△EDP=S梯形ABPE;
S?AGPE=S梯形ABPE﹣S△GBP=S梯形BPHC﹣S△FPB=S?FPHC;
(2)S?AGHD=S?AGPE+S?HDPE=S?PFCH+S?PHDE=S?EFCD;
(3)S?ABFE=S?AGPE+S?GBFP=S?PFCH+S?GBFP=S?GBCH.
故选:C.
【点评】考查了矩形的性质,本题是一道结论开放题,掌握矩形的性质,很容易得到答案.
3.下列四个图案中,符合如图所示的胶筒滚动后的图案是( )
A. B. C. D.
【分析】根据旋转的性质,找出图中三角形排列规律从左到右的方向滚涂到墙上图案即可选择答案.
【解答】解:根据旋转的性质和胶滚上的图案可知,横向状态转为正立状态,胶滚滚出的图案是.
故选:A.
【点评】本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
4.把正方体的六个面分别涂上白,黄,蓝,红,紫,绿六种不同的颜色,将上述大小相同,颜色分布一样的,四个正方体,拼成一个平面放置的长方体,如图所示,则正方体中与白色面相对的面的颜色是( )
A.黄色 B.蓝色 C.紫色 D.绿色
【分析】以“红色”为突破口,红色与紫色、黄色、白色、蓝色相邻,所以红色的对面是绿色;黄色与红色、白色、蓝色、绿色相邻,所以黄色的对面是紫色,则剩余的白色与蓝色相对.
【解答】解:最右边的正方体告诉我们:红色与蓝色、黄色相邻,中间两个正方体告诉我们:红色与紫色、白色相邻,所以红色的对面是绿色;又黄色与红色、白色、蓝色、绿色相邻,所以黄色的对面是紫色,则剩余的白色与蓝色相对.
故选:B.
【点评】此题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
5.一个横截面为正方形的长方体,如果沿平行于横截面的方向截去长为2cm的一段后,成为一个正方体,这时侧面积减少了64cm2,则原长方体的表面积是( )
A.384cm2 B.448cm2 C.512cm2 D.640cm2
【分析】根据长截短2cm,就剩下一个正方体可知,这个正方体比原长方体表面积减少的4个面是相同的,根据已知侧面积减少了64cm2,64÷4÷2=8cm,求出减少面的宽,也就是剩下的正方体的棱长,然后8+2=10cm求出原长方体的长,再计算原长方体的表面积即可.
【解答】解:64÷4÷2=8(cm)
8×8×6+64
=384+64
=448(cm2)
答:原来长方体的表面积是448cm2.
故选:B.
【点评】考查了几何体的表面积,根据截去后剩下是正方体,可知减少的部分是宽为2cm的4个面,从而可以分别求出长方体的长、宽、高,进而利用长方体的表面积计算方法即可求解.
6.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
【分析】根据三视图的定义、结合图形对各个几何体进行观察即可判断,得到答案.
【解答】解:正方体从前往后看和从上往下看,看到的图形形状都是正方形,①符合题意;
球从前往后看和从上往下看,看到的图形形状都是圆,②符合题意;
圆锥从前往后看和从上往下看,看到的图形形状分别是三角形和圆,③不合题意;
圆柱从前往后看和从上往下看,看到的图形形状分别是矩形和圆,④不合题意,
故选:B.
【点评】本题考查的是简单几何体的三视图,理解三视图的概念、正确观察图形是解题的关键.
7.如图放置的几何体的左视图是( )
A. B. C. D.
【分析】根据从左边看得到的图形是左视图,可得答案.
【解答】解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
【点评】本题考查了简单组合体的三视图,从左边看得到的图形是左视图,注意中间看不到的线用虚线表示.
8.如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中面积最小的是( )
A.主视图 B.俯视图 C.左视图 D.一样大
【分析】如图可知该几何体的正视图由5个小正方形组成,左视图是由3个小正方形组成,俯视图是由5个小正方形组成,易得解.
【解答】解:如图,该几何体正视图是由5个小正方形组成,
左视图是由3个小正方形组成,
俯视图是由5个小正方形组成,
故三种视图面积最小的是左视图.
故选:C.
【点评】本题考查的是三视图的知识以及学生对该知识点的巩固.解题关键是找到三种视图的正方形的个数.
9.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
【分析】由几何体的主视图和俯视图可知,该几何体的主视图的第一列3个正方形中每个正方形所在位置最多均可有2个小立方块;最少一个正方形所在位置有2个小立方块,其余2个所在位置各有1个小立方块;主视图的第二列1个小正方形所在位置只能有1个.再根据用6个小立方块搭一个几何体即可求解.
【解答】解:这样的几何体不止一种,而有多种摆法.
最少需要2+1+1+1=5(个)小立方块,最多需要2×3+1=7(个)小立方块.
因为用6个小立方块搭一个几何体,
所以它的左视图不可能是.
故选:D.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖”就更容易得到答案.
10.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
【分析】首先根据主视图中有两条虚线,发现该几何体的应该有两条从正面看不到的棱,然后结合俯视图及提供的三个几何体确定正确的序号.
【解答】解:结合主视图和俯视图发现几何体的背面应该有个凸起,
故淘汰选项ABC,选D.
故选:D.
【点评】本题考查了由三视图判断几何体的知识,解题的关键是结合三视图及三个几何体确定正确的答案,难度不大.
二.填空题(共8小题)
11.三棱柱是由 5 个面围成,五棱柱有 10 个顶点.
【分析】根据三棱柱、五棱柱的概念和特性即可解.
【解答】解:三棱柱有2个底面,3个侧面,共5个面围成;五棱柱有10个顶点.
故答案为:5;10.
【点评】本题考查的是认识立体图形.柱体中,面与面相交成棱,棱与棱相交成顶点.
12.流星划过天空时留下一道明亮的光线,用数学知识解释为 点动成线. .
【分析】根据点动成线进行回答.
【解答】解:流星划过天空时留下一道明亮的光线,用数学知识解释为点动成线.
故答案为:点动成线.
【点评】此题主要考查了点、线、面、体,关键是掌握点动成线,线动成面,面动成体.
13.棱长为1.3cm的立方体的体积为 2.2 cm3;表面积为 1.7 cm2.(结果都保留2个有效数字)
【分析】根据立方体的体积V=a3,表面积S=6a2,列式计算即可求解..
【解答】解:1.33≈2.2(cm3),
1.32≈1.7(cm2).
故棱长为1.3cm的立方体的体积为2.2cm3;表面积为1.7cm2.
故答案为:2.2;1.7.
【点评】考查了几何体的体积和表面积,关键是熟悉立方体的体积V=a3,表面积S=6a2的知识点.
14.如图,图中共有 10 个梯形.
【分析】根据图形认真分析由图中可知一个梯形需一个平行四边形和一个三角形组成.
【解答】解:由图形的特点可知,一个平行四边形和一个三角形可组成一个梯形,且图形中的梯形的形状、大小相同,共有10个.
故答案为10.
【点评】有一组对边平行,另一组对边不平行的四边形是梯形.
15.一个长方体的主视图与俯视图如图所示,则这个长方体的表面积是 88 .
【分析】根据给出的长方体的主视图和俯视图可得,长方体的长是6,宽是2,高是4,进而可根据长方体的表面积公式求出其表面积.
【解答】解:由主视图可得长方体的长为6,高为4,
由俯视图可得长方体的宽为2,
则这个长方体的表面积是
(6×2+6×4+4×2)×2
=(12+24+8)×2
=44×2
=88.
故这个长方体的表面积是88.
故答案为:88.
【点评】考查由三视图判断几何体,长方体的表面积的求法,根据长方体的主视图和俯视图得到几何体的长、宽和高是解决本题的关键.
16.在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递堆如图所示,则这正方体快递件最多有 39 件.
【分析】由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得第3层最多正方体的个数为:3×2=6;由主视图和左视图可得第4层最多正方体的个数为:1;相加可得所求.
【解答】解:由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,
最底层几何体最多正方体的个数为:4×4=16,
由主视图和左视图可得第二层最多正方体的个数为:4×4=16;
由主视图和左视图可得第3层最多正方体的个数为:3×2=6;
由主视图和左视图可得第4层最多正方体的个数为:1;
16+16+6+1=39(件).
故这正方体快递件最多有39件.
故答案为:39.
【点评】此题考查由视图判断几何体;得到最底层正方体的最多的个数是解决本题的突破点;用到的知识点为:最底层正方体的最多的个数=行数×列数.
17.一个零件的主视图、左视图、俯视图如图所示(尺寸单位:厘米),这个零件的体积为 1800 立方厘米.
【分析】易得该几何体为长10,宽12,高15的长方体,长方体的体积=长×宽×高;
【解答】解:∵有2个视图为长方形,
∴该几何体为柱体,
∵第3个视图为长方形,
∴几何体为长方体,
∴长方体的体积为10×15×12=1800立方厘米.
故答案为:1800.
【点评】考查由视图判断几何体;用到的知识点为:有2个视图为长方形的几何体是柱体;得到该几何体长,宽,高是解决本题的突破点.
18.在画如图所示的几何体的三视图时,我们可以把它看成 圆锥 体和 圆柱 体的组合体.
【分析】由题意结合立体图形的特征可知,上部是圆锥,下部是圆柱,依此即可求解.
【解答】解:观察图形可知,在画如图所示的几何体的三视图时,我们可以把它看成圆锥体和圆柱体的组合体.
故答案为:圆锥;圆柱.
【点评】本题是基础题,考查几何体的三视图的识别能力,作图能力,三视图的投影规则是主视、俯视 长对正;主视、左视高平齐,左视、俯视宽相等.
三.解答题(共8小题)
19.推导猜测
(1)三棱锥有 6 条棱,四棱锥有 8 条棱,五棱锥有 10 条棱.
(2) 十五 棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是 五十 棱锥,面数是 51 .
【分析】(1)三棱锥侧面有3条棱,底面有3条棱,共有6条棱;四棱锥侧面有4条棱,底面有4条棱,共有8条棱;五棱锥侧面有5条棱,底面有5条棱,共有10条棱;
(2)共有30条棱,那么底面有15条棱,是十五棱锥;
(3)棱锥有100条棱,那么底面有50条棱,为五十棱锥,共有51个面.
【解答】解:(1)三棱锥有6条棱,四棱锥有8条棱,五棱锥有10条棱.
(2)十五棱锥有30条棱.
(3)一个棱锥的棱数是100,则这个棱锥是五十棱锥,面数是51.
故答案为:6,8,10;十五;五十,51.
【点评】考查了认识立体图形,关键是有规律的寻找多面体的棱及面的特点.
20.在下列两行图形中,分别找出相互对应的图形,并用线连接.
【分析】利用面动成体解答即可.
【解答】解:如图,
【点评】本题主要考查了点,线,面,体,解题的关键是培养学生的空间想象能力.
21.用边长为1的小正方块粘合成如图所示的模型,要在模型表面上涂油漆,如果除去粘合部分不涂外,求模型的涂漆面积.
【分析】顶层5个面外露,5个面被涂漆;二层2个正方体外露,6个侧面和2﹣1=1个顶面,7个面被涂漆;三层8个正方体外露,12个侧面和8﹣2=6个顶面,18个面被涂漆.
【解答】解:图形中11个正方体共有面:11×6=66(个);
被涂漆面共有:5+7+18=30(个);
所以被涂漆的表面积为:30×1×1+8=38.
答:模型的涂漆面积为38.
【点评】本题考查了几何体表面积的计算,解题的关键是得出粘合部分的面积,是基础知识要熟练掌握.
22.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
【分析】根据折叠情况,即可画出图形.
【解答】解:如图所示:
【点评】本题考查了学生对几何体的展开图的理解,以及空间想象能力.
23.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
【分析】(1)找到从正面和上面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
(2)根据题目所给尺寸,计算出下面长方体体积+上面圆柱的体积即可求解.
【解答】解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
【点评】此题主要考查了简单几何体的三视图,以及几何体的表面积,关键是掌握三视图所看的位置.
24.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
【分析】根据图形发挥空间想象能力作出图形即可.
【解答】解:从它的正面、左面、上面三个方向所看到的平面图形(每个图(2分) )
【点评】用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.
25.如图是由几个小立方块所搭成几何体从正面和从上面看的形状图:这样搭建的几何体,最少、最多各需要多少个小立方块?
【分析】易得这个几何体共有3层,由俯视图可得第一层正方体的个数,由主视图可得第二层和第三层最少或最多的正方体的个数,相加即可.
【解答】解:搭这样的几何体最少需要8+2+1=11个小正方体,
最多需要8+6+3=17个小正方体;
故最多需要17个小正方体,最少需要11个小正方体.
【点评】考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.
26.如图,一个几何体由若干个完全相同的小正方体组成,如图分别是从正面和上面看到的图形.
(1)该几何体最少需要 5 块小正方体;
(2)最多可以有 6 块小正方体.
【分析】(1)由俯视图可得最底层的几何体的个数,由主视图第二层正方形的个数可得第二层最少需要几块正方体,相加即可得到该几何体最少需要几块小正方体;
(2)由俯视图和主视图可得第二层最多需要几块小正方体,再加上最底层的正方体的个数即可得到最多可以有几块小正方体.
【解答】解:俯视图中有4个正方形,那么组合几何体的最底层有4个正方体,
(1)由主视图第二层有1个正方形可得组合几何体的第二层最少有1个正方体,
所以该几何体最少需要4+1=5块小正方体;
(2)主图从上边数第一行的第二层最多可有2个正方体,
所以该几何体最多需要4+2=6块小正方体.
故答案为:5,6.
【点评】考查由三视图判断几何体;用到的知识点为:俯视图正方形的个数为组合几何体最底层的正方体的个数;左视图第二层正方形的个数为组合几何体第二层的正方体最少的个数.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
