2019-2020学年苏科新版七年级上册数学《第6章 平面图形的认识(一)》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年苏科新版七年级上册数学《第6章 平面图形的认识(一)》单元测试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 00:00:00 | ||
图片预览




文档简介
2020年苏科新版七年级上册数学《第6章 平面图形的认识(一)》单元测试卷
一.选择题(共10小题)
1.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
2.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件l的直线共有( )条.
A.2 B.3 C.4 D.5
3.如图,一条街道旁有A,B,C,D,E五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 A B C D E
大桶水数/桶 38 55 50 72 85
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( )
A.B楼 B.C楼 C.D楼 D.E楼
4.点A,B,C在同一条直线上,AB=3cm,BC=1cm,则AC的长度为( )
A.2cm B.4cm C.2cm或4cm D.不能确定
5.如图(一),为一条拉直的细线,A、B两点在上,且:=1:3,:=3:5.若先固定B点,将折向,使得重迭在上,如图(二),再从图(二)的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
A.1:1:1 B.1:1:2 C.1:2:2 D.1:2:5
6.下列说法中:①因为对顶角相等,所以相等的两个角是对顶角;②在平面内,不相交的两条直线叫做平行线;③过一点有且只有一条直线与已知直线垂直.正确的是( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
8.下列四个说法:(1)线段AB是点A与点B之间的距离;(2)射线AB与射线BA表示同一条射线;(3)经过一点有且只有一条直线与已知直线平行;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.下列语句正确的是( )
A.平角是直线
B.画5cm长的射线
C.平行线就是不相交的两条直线
D.在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
10.下列说法正确的是( )
A.不相交的两条射线一定平行
B.在同一平面内,过一点有且只有一条直线与这条直线平行
C.在同一平面内,过一点有且只有一条直线与这条直线垂直
D.直线外一点与直线上任一点的连线段叫做点到直线的距离
二.填空题(共8小题)
11.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的有 (只填写序号).
12.平面上的7条直线,最多能有 个交点.
13.如图,乐乐用剪刀沿直线将一片平整的树叶减掉一部分,发现剩下树叶的周长比原周长小,能正确解释这一现象的数学依据是 .
14.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长 .
15.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
16.已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=72°,则∠BOD= .
17.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数 .
18.如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据: .
三.解答题(共8小题)
19.已知,A、B、C三点,按下列要求作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA、AB上分别取C、D,画直线CD.
20.请你做裁判:过三点中的两点作直线,小明说有一条,小林说有三条,小红说不是一条就是三条,你认为他们三人谁的说法正确?为什么?
21.如图,在直线a上求一点O,使它到点M、N的距离最小.
22.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 ,数轴上表示﹣2和3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
23.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
24.如图,直线AB,CD相交于点O,∠AOC=60°,∠1:∠2=1:2.
(1)求∠2的度数;
(2)若∠2与∠MOE互余,求∠MOB的度数.
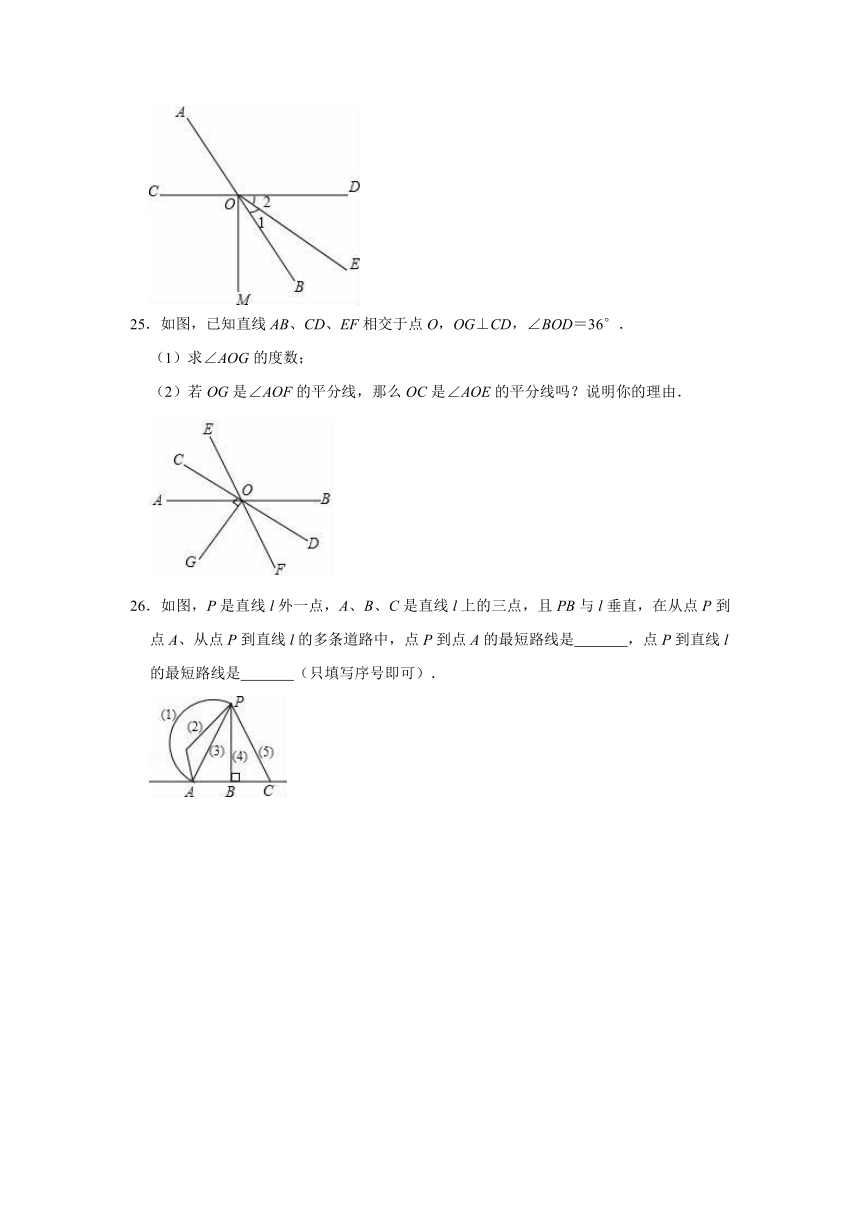
25.如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
26.如图,P是直线l外一点,A、B、C是直线l上的三点,且PB与l垂直,在从点P到点A、从点P到直线l的多条道路中,点P到点A的最短路线是 ,点P到直线l的最短路线是 (只填写序号即可).
2020年苏科新版七年级上册数学《第6章 平面图形的认识(一)》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
【分析】求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
【解答】解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
则m+n=1+36=37
故选:B.
【点评】此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
2.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件l的直线共有( )条.
A.2 B.3 C.4 D.5
【分析】根据题意,可以分别以A、B为圆心,以2cm,3cm为半径画圆,然后求两圆的公切线,公切线的条数就是直线l的条数.
【解答】解:如图所示:
∵AB=5,点A、B到直线l的距离分别等于2、3,
∴⊙A与⊙B外切,共有3条公切线,
∴满足条件l的直线共有3条.
故选:B.
【点评】本题考查的是两点确定一条直线,题中数据AB=5与点A、B到直线l的距离分别等于2、3起到了关键的限制作用,利用数形结合进行解答更形象直观.
3.如图,一条街道旁有A,B,C,D,E五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 A B C D E
大桶水数/桶 38 55 50 72 85
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( )
A.B楼 B.C楼 C.D楼 D.E楼
【分析】此题为数学知识的应用,由题意设立大桶水供应点,肯定要尽量缩短居民取水所走路程之间的里程,即需应用两点间线段最短定理来求解.
【解答】解:设AB=a,BC=b,CD=c,DE=d.每户居民每次取一桶水.
以点A为取水点,则五幢楼内的居民取水所走路程之和=55AB+50AC+72AD+85AE=262a+207b+157c+85d,
以点B为取水点,则五幢楼内的居民取水所走路程之和=38AB+50BC+72BD+85BE=38a+207b+157c+85d,
以点C为取水点,则五幢楼内的居民取水所走路程之和=38AC+55BC+72CD+85CE=38a+93b+157c+85d,
以点D为取水点,则五幢楼内的居民取水所走路程之和=38AD+55BD+50CD+85DE=38a+93b+143c+85d,
以点E为取水点,则五幢楼内的居民取水所走路程之和=38AE+55BE+50CE+72DE=38a+93b+143c+215d,
以点D为取水点,五幢楼内的居民取水所走路程之和最小.
故选:C.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
4.点A,B,C在同一条直线上,AB=3cm,BC=1cm,则AC的长度为( )
A.2cm B.4cm C.2cm或4cm D.不能确定
【分析】本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意画出的图形进行解答.
【解答】解:本题有两种情形:
(1)当点C在线段AB上时,如图,AC=AB﹣BC,
又∵AB=3cm,BC=1cm,
∴AC=3﹣1=2cm;
(2)当点C在线段AB的延长线上时,如图,AC=AB+BC,
又∵AB=3cm,BC=1cm,
∴AC=3+1=4cm.
故线段AC=2cm或4cm.
故选:C.
【点评】考查了两点间的距离,在未画图类问题中,正确画图很重要,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
5.如图(一),为一条拉直的细线,A、B两点在上,且:=1:3,:=3:5.若先固定B点,将折向,使得重迭在上,如图(二),再从图(二)的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
A.1:1:1 B.1:1:2 C.1:2:2 D.1:2:5
【分析】根据题意可以设出线段OP的长度,从而根据比值可以得到图一中各线段的长,根据题意可以求出折叠后,再剪开各线段的长度,从而可以求得三段细线由小到大的长度比,本题得以解决.
【解答】解:设OP的长度为8a,
∵OA:AP=1:3,OB:BP=3:5,
∴OA=2a,AP=6a,OB=3a,BP=5a,
又∵先固定B点,将OB折向BP,使得OB重迭在BP上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,
∴这三段从小到大的长度分别是:2a、2a、4a,
∴此三段细线由小到大的长度比为:2a:2a:4a=1:1:2,
故选:B.
【点评】本题考查比较线段的长短,解题的关键是理解题意,求出各线段的长度.
6.下列说法中:①因为对顶角相等,所以相等的两个角是对顶角;②在平面内,不相交的两条直线叫做平行线;③过一点有且只有一条直线与已知直线垂直.正确的是( )
A.0个 B.1个 C.2个 D.3个
【分析】①对顶角相等,反过来不成立;①不正确;②平行线的定义;②正确;③在同一平面内,命题才成立.
【解答】解:①不正确;相等的角不一定是对顶角;
②正确;这是平行线的定义;
③不正确;必须是在同一平面内;
故选:B.
【点评】本题考查了对顶角的性质、平行线的定义以及垂线的性质;正确理解定义、定理是解题的关键.
7.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
【分析】根据邻补角定义,两个角的和等于180°,并且有一条边是公共边的两个角互为邻补角,进行解答.
【解答】解:如图,邻补角有:∠AOC与∠AOD,∠AOD与∠BOD,∠BOD与∠BOC,∠BOE与∠AOE,∠BOC与∠AOC,∠COE与∠DOE.
所以共6对.
故选:B.
【点评】本题主要考查邻补角的定义,注意按一定顺序寻找方能做到不重不漏.
8.下列四个说法:(1)线段AB是点A与点B之间的距离;(2)射线AB与射线BA表示同一条射线;(3)经过一点有且只有一条直线与已知直线平行;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的概念,两点间的距离和点到直线的距离以及平行线的性质作答.
【解答】解:(1)线段AB的长度是点A与点B之间的距离,所以错误;
(2)射线AB与射线BA表示方向相反的两条射线,所以错误;
(3)经过直线外一点有且只有一条直线与已知直线平行,所以错误;
(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,正确.
故选:A.
【点评】对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
9.下列语句正确的是( )
A.平角是直线
B.画5cm长的射线
C.平行线就是不相交的两条直线
D.在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
【分析】根据角的定义即可判断A;根据射线的性质进行判断B;根据平行线的定义即可判断C;根据在同一平面内,两条不重合的直线的位置关系即可判断D.
【解答】解:A,根据角的定义,角是有公共端点的两条射线组成的图形,故本选项错误;
B、射线没有长度,故本选项错误;
C、平行线是指在同一平面内,不相交的直线,故本选项错误;
D、在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行,故本选项正确.
故选:D.
【点评】本题主要考查对平行线的定义,射线的定义,角的定义等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
10.下列说法正确的是( )
A.不相交的两条射线一定平行
B.在同一平面内,过一点有且只有一条直线与这条直线平行
C.在同一平面内,过一点有且只有一条直线与这条直线垂直
D.直线外一点与直线上任一点的连线段叫做点到直线的距离
【分析】根据射线在一直线上课判断A;根据平行公理的推论课判断B;根据点到直线的距离定义可判断D;根据垂线的性质可判断C.
【解答】解:A、当两射线在一直线上时就不平行,故本选项错误;
B、过直线外一点有且只有一条直线平行于已知直线,故本选项错误;
C、在同一平面内,过一点有且只有一条直线垂直于已知直线,故本选项正确;
D、过直线外一点作直线的垂线,这点和垂足之间的线段的长是点到直线的距离,故本选项错误;
故选:C.
【点评】本题考查了对平行公理及推论,垂线,点到直线的距离等知识点的应用,关键是能根据定理和性质进行判断.
二.填空题(共8小题)
11.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的有 ③ (只填写序号).
【分析】根据直线与点的位置关系即可求解.
【解答】解:①点A在直线BC上是错误的;
②直线AB经过点C是错误的;
③直线AB,BC,CA两两相交是正确的;
④点B是直线AB,BC,CA的公共点是错误的.
故答案为:③.
【点评】考查了直线、射线、线段,关键是熟练掌握直线、射线、线段的定义,是基础题型.
12.平面上的7条直线,最多能有 21 个交点.
【分析】通过画图和观察图形得到2条直线最多的交点个数为1,3条直线最多的交点个数为1+2=3,4条直线最多的交点个数为1+2+3=6,5条直线最多的交点个数为1+2+3+4=10,…,则n条直线最多的交点个数为1+2+3+4+…+n﹣1,然后把n=7代入计算.
【解答】解:2条直线最多的交点个数为1,
3条直线最多的交点个数为1+2=3,
4条直线最多的交点个数为1+2+3=6,
5条直线最多的交点个数为1+2+3+4=10,
…
所以7条直线最多的交点个数为1+2+3+4+5+6=21.
故答案为:21.
【点评】考查了直线的性质:两点确定一条直线,此题在相交线的基础上,着重培养学生的观察、实验能力.
13.如图,乐乐用剪刀沿直线将一片平整的树叶减掉一部分,发现剩下树叶的周长比原周长小,能正确解释这一现象的数学依据是 两点之间线段最短 .
【分析】根据线段的性质,可得答案.
【解答】解:∵两点之间线段最短,
∴剩下树叶的周长比原树叶的周长小.
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,利用线段的性质是解题关键.
14.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长 5cm .
【分析】依据C为AO的中点,D为OB的中点,即可得到CO=AO,OD=OB.再根据AB=10cm,即可得到CD的长.
【解答】解:∵C为AO的中点,D为OB的中点,
∴CO=AO,OD=OB
∴CD=CO+OD=?AO+?OB=(AO+OB)=?AB=?10=5cm.
故答案为:5cm.
【点评】本题考查了两点间的距离,平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度.
15.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 46 .
【分析】由题意可得10条直线相交于一点时交点最少,任意两直线相交都产生一个交点时交点最多,由此可得出m,n的值,从而得出答案.
【解答】解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
【点评】本题考查直线的交点问题,注意掌握直线相交于一点时交点最少,任意n条直线两两相交时交点最多为n(n﹣1)个.
16.已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=72°,则∠BOD= 36° .
【分析】由角平分线的定义求出∠AOC=36°,再由对顶角相等即可得出∠BOD的度数.
【解答】解:∵OA平分∠EOC,∠EOC=72°,
∴∠AOC=∠EOC=36°,
∴∠BOD=∠AOC=36°;
故答案为:36°.
【点评】本题考查了角平分线的定义、对顶角相等的性质;熟练掌握角平分线的定义,由对顶角相等得出∠BOD是解决问题的关键.
17.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数 40°或140° .
【分析】根据题意可知,射线OC、OD可能在直线AB的同侧,也可能在直线AB的异侧,分两种情况进行讨论即可.
【解答】解:由OC⊥OD,可得∠DOC=90°,
如图1,当∠AOC=50°时,∠BOD=180°﹣50°﹣90°=40°;
如图2,当∠AOC=50°时,∠AOD=90°﹣50°=40°,此时,∠BOD=180°﹣∠AOD=140°.
故答案为:40°或140°
【点评】本题主要考查了垂线的定义,解决问题的关键是根据题意画出图形,解题时注意分类讨论思想的运用.
18.如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据: 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
【点评】本题考查了垂线的性质在实际生活中的运用,关键是掌握垂线段的性质:垂线段最短.
三.解答题(共8小题)
19.已知,A、B、C三点,按下列要求作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA、AB上分别取C、D,画直线CD.
【分析】根据直线没有端点,射线有一个端点,线段有两个端点,可得答案.
【解答】解:如图所示:
【点评】本题考查了作图,注意直线不能有端点,线段要画出端点,连接两点得出线段.
20.请你做裁判:过三点中的两点作直线,小明说有一条,小林说有三条,小红说不是一条就是三条,你认为他们三人谁的说法正确?为什么?
【分析】过三点中的两点作直线有两种情况,即若三点在同一条直线上则可确定一条直线;若三点不在同一条直线上可确定三条直线.
【解答】解:如图所示:
当三点如图(一)所示时可确定一条直线;
当三点如图(二)所示时可确定三条直线.
故小红说的正确.
【点评】本题考查的是直线的性质,解答此题的关键是确定三点的位置关系,不要漏解.
21.如图,在直线a上求一点O,使它到点M、N的距离最小.
【分析】要使OM+ON的值最小,只需M、N、O三点共线即可.
【解答】解:∵两点之间线段最短,
∴所求的点与M、N两点同线时,它到点M、N的距离最小,
∴连接MN.MN与a的交点O即为所求.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
22.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 4 ,数轴上表示﹣2和3的两点之间的距离是 5 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 |x+1| ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
【分析】(1)(2)在数轴上A、B两点之间的距离为AB=|a﹣b|,依此即可求解;
(3)根据绝对值的性质去掉绝对值号,然后计算即可得解
【解答】解:(1)|1﹣(﹣3)|=4;|3﹣(﹣2)|=5;
故答案为:4;5;
(2)|x﹣(﹣1)|=|x+1|或|(﹣1)﹣x|=|x+1|,
故答案为:|x+1|;
(3)有最小值,
当x<﹣3时,|x﹣2|+|x+3|=2﹣x﹣x﹣3=﹣2x﹣1,
当﹣3≤x≤2时,|x﹣2|+|x+3|=2﹣x+x+3=5,
当x>2时,|x﹣2|+|x+3|=x﹣2+x+3=2x+1,
在数轴上|x﹣2|+|x+3|的几何意义是:表示有理数x的点到﹣3及到2的距离之和,所以当﹣3≤x≤2时,它的最小值为5.
【点评】本题考查了数轴,绝对值的性质,读懂题目信息,理解数轴上两点间的距离的表示是解题的关键.注意分类思想在解题中的运用.
23.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
【分析】根据直线两两相交,每三条不交于同一点,可把平面分成最多部分,根据两条直线最多分成的部分比一条直线分成部分增加2,三条直线最多分成部分比两条直线最多分成部分增加三,以此类推,可得答案.
【解答】解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
【点评】本题考查了相交线,由图形得出规律是解题关键,规律1条直线分成两部分,两条直线增加2,三条直线再增加三,四条直线再增加四….
24.如图,直线AB,CD相交于点O,∠AOC=60°,∠1:∠2=1:2.
(1)求∠2的度数;
(2)若∠2与∠MOE互余,求∠MOB的度数.
【分析】(1)根据对顶角相等得到∠DOB=60°,根据已知求出∠2的度数;
(2)根据余角的概念求出∠MOE的度数,计算即可.
【解答】解:(1)∵∠DOB=∠AOC=60°,
∴∠1+∠2=60°,又∠1:∠2=1:2.
∴∠1=20°,∠2=40°;
(2)∵∠2与∠MOE互余,∠2=40°,
∴∠MOE=50°,又∠1=20°,
∴∠MOB=30°.
【点评】本题考查的是对顶角、邻补角的概念和余角补角的概念,掌握对顶角相等、如果两个角的和等于90°(直角),就说这两个角互为余角是解题的关键.
25.如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
【分析】(1)根据对顶角的性质可得∠AOC=∠BOD=36°,利用垂直定义可得∠COG=90°,然后再计算出∠AOG的度数即可;
(2)根据角平分线定义以及垂直定义可得∠COA=∠DOF,再根据对顶角相等可得∠DOF=∠COE,进而得出∠AOC=∠COE,即可得到OC平分∠AOE.
【解答】解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°﹣∠AOC=90°﹣36o=54o;
(2)OC是∠AOE的平分线.
∵OG是∠AOF的角平分线,
∴∠AOG=∠GOF,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠COA=∠DOF,
又∵∠DOF=∠COE,
∴∠AOC=∠COE,
∴OC平分∠AOE.
【点评】此题主要考查了角平分线的定义以及垂线,关键是掌握角平分线把角分成相等的两部分,注意理清图中角之间的关系.
26.如图,P是直线l外一点,A、B、C是直线l上的三点,且PB与l垂直,在从点P到点A、从点P到直线l的多条道路中,点P到点A的最短路线是 (3) ,点P到直线l的最短路线是 (4) (只填写序号即可).
【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;从直线外一点到这条直线上各点所连的线段中,垂线段最短.填空.
【解答】解:①因为两点之间线段最短,所以在连接PA的所有路线中,点P到点A的最短路线是(3),(1分)
②线段BP是点P到直线L的垂线段,根据垂线段最短可知,(1)~(5)中,PB最短,所以点P到直线l的最短路线是(4).(2分)
故答案是:(3)、(4).
【点评】本题主要考查了垂线段最短的性质和点到直线的距离的概念.
一.选择题(共10小题)
1.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
2.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件l的直线共有( )条.
A.2 B.3 C.4 D.5
3.如图,一条街道旁有A,B,C,D,E五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 A B C D E
大桶水数/桶 38 55 50 72 85
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( )
A.B楼 B.C楼 C.D楼 D.E楼
4.点A,B,C在同一条直线上,AB=3cm,BC=1cm,则AC的长度为( )
A.2cm B.4cm C.2cm或4cm D.不能确定
5.如图(一),为一条拉直的细线,A、B两点在上,且:=1:3,:=3:5.若先固定B点,将折向,使得重迭在上,如图(二),再从图(二)的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
A.1:1:1 B.1:1:2 C.1:2:2 D.1:2:5
6.下列说法中:①因为对顶角相等,所以相等的两个角是对顶角;②在平面内,不相交的两条直线叫做平行线;③过一点有且只有一条直线与已知直线垂直.正确的是( )
A.0个 B.1个 C.2个 D.3个
7.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
8.下列四个说法:(1)线段AB是点A与点B之间的距离;(2)射线AB与射线BA表示同一条射线;(3)经过一点有且只有一条直线与已知直线平行;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.下列语句正确的是( )
A.平角是直线
B.画5cm长的射线
C.平行线就是不相交的两条直线
D.在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
10.下列说法正确的是( )
A.不相交的两条射线一定平行
B.在同一平面内,过一点有且只有一条直线与这条直线平行
C.在同一平面内,过一点有且只有一条直线与这条直线垂直
D.直线外一点与直线上任一点的连线段叫做点到直线的距离
二.填空题(共8小题)
11.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的有 (只填写序号).
12.平面上的7条直线,最多能有 个交点.
13.如图,乐乐用剪刀沿直线将一片平整的树叶减掉一部分,发现剩下树叶的周长比原周长小,能正确解释这一现象的数学依据是 .
14.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长 .
15.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 .
16.已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=72°,则∠BOD= .
17.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数 .
18.如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据: .
三.解答题(共8小题)
19.已知,A、B、C三点,按下列要求作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA、AB上分别取C、D,画直线CD.
20.请你做裁判:过三点中的两点作直线,小明说有一条,小林说有三条,小红说不是一条就是三条,你认为他们三人谁的说法正确?为什么?
21.如图,在直线a上求一点O,使它到点M、N的距离最小.
22.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 ,数轴上表示﹣2和3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
23.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
24.如图,直线AB,CD相交于点O,∠AOC=60°,∠1:∠2=1:2.
(1)求∠2的度数;
(2)若∠2与∠MOE互余,求∠MOB的度数.
25.如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
26.如图,P是直线l外一点,A、B、C是直线l上的三点,且PB与l垂直,在从点P到点A、从点P到直线l的多条道路中,点P到点A的最短路线是 ,点P到直线l的最短路线是 (只填写序号即可).
2020年苏科新版七年级上册数学《第6章 平面图形的认识(一)》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
【分析】求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
【解答】解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
则m+n=1+36=37
故选:B.
【点评】此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
2.已知A、B为平面上的2个定点,且AB=5.若点A、B到直线l的距离分别等于2、3,则满足条件l的直线共有( )条.
A.2 B.3 C.4 D.5
【分析】根据题意,可以分别以A、B为圆心,以2cm,3cm为半径画圆,然后求两圆的公切线,公切线的条数就是直线l的条数.
【解答】解:如图所示:
∵AB=5,点A、B到直线l的距离分别等于2、3,
∴⊙A与⊙B外切,共有3条公切线,
∴满足条件l的直线共有3条.
故选:B.
【点评】本题考查的是两点确定一条直线,题中数据AB=5与点A、B到直线l的距离分别等于2、3起到了关键的限制作用,利用数形结合进行解答更形象直观.
3.如图,一条街道旁有A,B,C,D,E五幢居民楼.某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 A B C D E
大桶水数/桶 38 55 50 72 85
他们计划在这五幢楼中租赁一间门市房,设立大桶水供应点.若仅考虑这五幢楼内的居民取水所走路程之和最小,可以选择的地点应在( )
A.B楼 B.C楼 C.D楼 D.E楼
【分析】此题为数学知识的应用,由题意设立大桶水供应点,肯定要尽量缩短居民取水所走路程之间的里程,即需应用两点间线段最短定理来求解.
【解答】解:设AB=a,BC=b,CD=c,DE=d.每户居民每次取一桶水.
以点A为取水点,则五幢楼内的居民取水所走路程之和=55AB+50AC+72AD+85AE=262a+207b+157c+85d,
以点B为取水点,则五幢楼内的居民取水所走路程之和=38AB+50BC+72BD+85BE=38a+207b+157c+85d,
以点C为取水点,则五幢楼内的居民取水所走路程之和=38AC+55BC+72CD+85CE=38a+93b+157c+85d,
以点D为取水点,则五幢楼内的居民取水所走路程之和=38AD+55BD+50CD+85DE=38a+93b+143c+85d,
以点E为取水点,则五幢楼内的居民取水所走路程之和=38AE+55BE+50CE+72DE=38a+93b+143c+215d,
以点D为取水点,五幢楼内的居民取水所走路程之和最小.
故选:C.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
4.点A,B,C在同一条直线上,AB=3cm,BC=1cm,则AC的长度为( )
A.2cm B.4cm C.2cm或4cm D.不能确定
【分析】本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意画出的图形进行解答.
【解答】解:本题有两种情形:
(1)当点C在线段AB上时,如图,AC=AB﹣BC,
又∵AB=3cm,BC=1cm,
∴AC=3﹣1=2cm;
(2)当点C在线段AB的延长线上时,如图,AC=AB+BC,
又∵AB=3cm,BC=1cm,
∴AC=3+1=4cm.
故线段AC=2cm或4cm.
故选:C.
【点评】考查了两点间的距离,在未画图类问题中,正确画图很重要,本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
5.如图(一),为一条拉直的细线,A、B两点在上,且:=1:3,:=3:5.若先固定B点,将折向,使得重迭在上,如图(二),再从图(二)的A点及与A点重迭处一起剪开,使得细线分成三段,则此三段细线由小到大的长度比为何?( )
A.1:1:1 B.1:1:2 C.1:2:2 D.1:2:5
【分析】根据题意可以设出线段OP的长度,从而根据比值可以得到图一中各线段的长,根据题意可以求出折叠后,再剪开各线段的长度,从而可以求得三段细线由小到大的长度比,本题得以解决.
【解答】解:设OP的长度为8a,
∵OA:AP=1:3,OB:BP=3:5,
∴OA=2a,AP=6a,OB=3a,BP=5a,
又∵先固定B点,将OB折向BP,使得OB重迭在BP上,如图(二),再从图(二) 的A点及与A点重迭处一起剪开,使得细线分成三段,
∴这三段从小到大的长度分别是:2a、2a、4a,
∴此三段细线由小到大的长度比为:2a:2a:4a=1:1:2,
故选:B.
【点评】本题考查比较线段的长短,解题的关键是理解题意,求出各线段的长度.
6.下列说法中:①因为对顶角相等,所以相等的两个角是对顶角;②在平面内,不相交的两条直线叫做平行线;③过一点有且只有一条直线与已知直线垂直.正确的是( )
A.0个 B.1个 C.2个 D.3个
【分析】①对顶角相等,反过来不成立;①不正确;②平行线的定义;②正确;③在同一平面内,命题才成立.
【解答】解:①不正确;相等的角不一定是对顶角;
②正确;这是平行线的定义;
③不正确;必须是在同一平面内;
故选:B.
【点评】本题考查了对顶角的性质、平行线的定义以及垂线的性质;正确理解定义、定理是解题的关键.
7.如图,直线AB、CD相交于点O,作射线OE,则图中邻补角有( )
A.4对 B.6对 C.7对 D.8对
【分析】根据邻补角定义,两个角的和等于180°,并且有一条边是公共边的两个角互为邻补角,进行解答.
【解答】解:如图,邻补角有:∠AOC与∠AOD,∠AOD与∠BOD,∠BOD与∠BOC,∠BOE与∠AOE,∠BOC与∠AOC,∠COE与∠DOE.
所以共6对.
故选:B.
【点评】本题主要考查邻补角的定义,注意按一定顺序寻找方能做到不重不漏.
8.下列四个说法:(1)线段AB是点A与点B之间的距离;(2)射线AB与射线BA表示同一条射线;(3)经过一点有且只有一条直线与已知直线平行;(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】根据射线的概念,两点间的距离和点到直线的距离以及平行线的性质作答.
【解答】解:(1)线段AB的长度是点A与点B之间的距离,所以错误;
(2)射线AB与射线BA表示方向相反的两条射线,所以错误;
(3)经过直线外一点有且只有一条直线与已知直线平行,所以错误;
(4)直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,正确.
故选:A.
【点评】对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义,要善于区分不同概念之间的联系和区别.
9.下列语句正确的是( )
A.平角是直线
B.画5cm长的射线
C.平行线就是不相交的两条直线
D.在同一平面内,两条不重合的直线的位置关系只有两种:相交或平行
【分析】根据角的定义即可判断A;根据射线的性质进行判断B;根据平行线的定义即可判断C;根据在同一平面内,两条不重合的直线的位置关系即可判断D.
【解答】解:A,根据角的定义,角是有公共端点的两条射线组成的图形,故本选项错误;
B、射线没有长度,故本选项错误;
C、平行线是指在同一平面内,不相交的直线,故本选项错误;
D、在同一平面内,两条不重合的直线的位置关系只有两种:相交和平行,故本选项正确.
故选:D.
【点评】本题主要考查对平行线的定义,射线的定义,角的定义等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
10.下列说法正确的是( )
A.不相交的两条射线一定平行
B.在同一平面内,过一点有且只有一条直线与这条直线平行
C.在同一平面内,过一点有且只有一条直线与这条直线垂直
D.直线外一点与直线上任一点的连线段叫做点到直线的距离
【分析】根据射线在一直线上课判断A;根据平行公理的推论课判断B;根据点到直线的距离定义可判断D;根据垂线的性质可判断C.
【解答】解:A、当两射线在一直线上时就不平行,故本选项错误;
B、过直线外一点有且只有一条直线平行于已知直线,故本选项错误;
C、在同一平面内,过一点有且只有一条直线垂直于已知直线,故本选项正确;
D、过直线外一点作直线的垂线,这点和垂足之间的线段的长是点到直线的距离,故本选项错误;
故选:C.
【点评】本题考查了对平行公理及推论,垂线,点到直线的距离等知识点的应用,关键是能根据定理和性质进行判断.
二.填空题(共8小题)
11.直线AB,BC,CA的位置关系如图所示,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB,BC,CA两两相交;④点B是直线AB,BC,CA的公共点,正确的有 ③ (只填写序号).
【分析】根据直线与点的位置关系即可求解.
【解答】解:①点A在直线BC上是错误的;
②直线AB经过点C是错误的;
③直线AB,BC,CA两两相交是正确的;
④点B是直线AB,BC,CA的公共点是错误的.
故答案为:③.
【点评】考查了直线、射线、线段,关键是熟练掌握直线、射线、线段的定义,是基础题型.
12.平面上的7条直线,最多能有 21 个交点.
【分析】通过画图和观察图形得到2条直线最多的交点个数为1,3条直线最多的交点个数为1+2=3,4条直线最多的交点个数为1+2+3=6,5条直线最多的交点个数为1+2+3+4=10,…,则n条直线最多的交点个数为1+2+3+4+…+n﹣1,然后把n=7代入计算.
【解答】解:2条直线最多的交点个数为1,
3条直线最多的交点个数为1+2=3,
4条直线最多的交点个数为1+2+3=6,
5条直线最多的交点个数为1+2+3+4=10,
…
所以7条直线最多的交点个数为1+2+3+4+5+6=21.
故答案为:21.
【点评】考查了直线的性质:两点确定一条直线,此题在相交线的基础上,着重培养学生的观察、实验能力.
13.如图,乐乐用剪刀沿直线将一片平整的树叶减掉一部分,发现剩下树叶的周长比原周长小,能正确解释这一现象的数学依据是 两点之间线段最短 .
【分析】根据线段的性质,可得答案.
【解答】解:∵两点之间线段最短,
∴剩下树叶的周长比原树叶的周长小.
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,利用线段的性质是解题关键.
14.如图,AB=10cm,O为线段AB上的任意一点,C为AO的中点,D为OB的中点,则线段CD长 5cm .
【分析】依据C为AO的中点,D为OB的中点,即可得到CO=AO,OD=OB.再根据AB=10cm,即可得到CD的长.
【解答】解:∵C为AO的中点,D为OB的中点,
∴CO=AO,OD=OB
∴CD=CO+OD=?AO+?OB=(AO+OB)=?AB=?10=5cm.
故答案为:5cm.
【点评】本题考查了两点间的距离,平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度.
15.平面内有10条直线两两相交,交点个数最多有m个,最少有n个,则m+n的值为 46 .
【分析】由题意可得10条直线相交于一点时交点最少,任意两直线相交都产生一个交点时交点最多,由此可得出m,n的值,从而得出答案.
【解答】解:根据题意可得:10条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:10×(10﹣1)÷2=45,
即m=45;
则m+n=45+1=46.
故答案为:46.
【点评】本题考查直线的交点问题,注意掌握直线相交于一点时交点最少,任意n条直线两两相交时交点最多为n(n﹣1)个.
16.已知:如图,直线AB、CD相交于点O,OA平分∠EOC,若∠EOC=72°,则∠BOD= 36° .
【分析】由角平分线的定义求出∠AOC=36°,再由对顶角相等即可得出∠BOD的度数.
【解答】解:∵OA平分∠EOC,∠EOC=72°,
∴∠AOC=∠EOC=36°,
∴∠BOD=∠AOC=36°;
故答案为:36°.
【点评】本题考查了角平分线的定义、对顶角相等的性质;熟练掌握角平分线的定义,由对顶角相等得出∠BOD是解决问题的关键.
17.过直线AB上一点O作射线OC、OD,使OC⊥OD,当∠AOC=50°时,则∠BOD的度数 40°或140° .
【分析】根据题意可知,射线OC、OD可能在直线AB的同侧,也可能在直线AB的异侧,分两种情况进行讨论即可.
【解答】解:由OC⊥OD,可得∠DOC=90°,
如图1,当∠AOC=50°时,∠BOD=180°﹣50°﹣90°=40°;
如图2,当∠AOC=50°时,∠AOD=90°﹣50°=40°,此时,∠BOD=180°﹣∠AOD=140°.
故答案为:40°或140°
【点评】本题主要考查了垂线的定义,解决问题的关键是根据题意画出图形,解题时注意分类讨论思想的运用.
18.如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据: 垂线段最短 .
【分析】过直线外一点作直线的垂线,这一点与垂足之间的线段就是垂线段,且垂线段最短.据此作答.
【解答】解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
【点评】本题考查了垂线的性质在实际生活中的运用,关键是掌握垂线段的性质:垂线段最短.
三.解答题(共8小题)
19.已知,A、B、C三点,按下列要求作图:
(1)连接AB;
(2)画射线OA,BO;
(3)在线段OA、AB上分别取C、D,画直线CD.
【分析】根据直线没有端点,射线有一个端点,线段有两个端点,可得答案.
【解答】解:如图所示:
【点评】本题考查了作图,注意直线不能有端点,线段要画出端点,连接两点得出线段.
20.请你做裁判:过三点中的两点作直线,小明说有一条,小林说有三条,小红说不是一条就是三条,你认为他们三人谁的说法正确?为什么?
【分析】过三点中的两点作直线有两种情况,即若三点在同一条直线上则可确定一条直线;若三点不在同一条直线上可确定三条直线.
【解答】解:如图所示:
当三点如图(一)所示时可确定一条直线;
当三点如图(二)所示时可确定三条直线.
故小红说的正确.
【点评】本题考查的是直线的性质,解答此题的关键是确定三点的位置关系,不要漏解.
21.如图,在直线a上求一点O,使它到点M、N的距离最小.
【分析】要使OM+ON的值最小,只需M、N、O三点共线即可.
【解答】解:∵两点之间线段最短,
∴所求的点与M、N两点同线时,它到点M、N的距离最小,
∴连接MN.MN与a的交点O即为所求.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
22.阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 4 ,数轴上表示﹣2和3的两点之间的距离是 5 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 |x+1| ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
【分析】(1)(2)在数轴上A、B两点之间的距离为AB=|a﹣b|,依此即可求解;
(3)根据绝对值的性质去掉绝对值号,然后计算即可得解
【解答】解:(1)|1﹣(﹣3)|=4;|3﹣(﹣2)|=5;
故答案为:4;5;
(2)|x﹣(﹣1)|=|x+1|或|(﹣1)﹣x|=|x+1|,
故答案为:|x+1|;
(3)有最小值,
当x<﹣3时,|x﹣2|+|x+3|=2﹣x﹣x﹣3=﹣2x﹣1,
当﹣3≤x≤2时,|x﹣2|+|x+3|=2﹣x+x+3=5,
当x>2时,|x﹣2|+|x+3|=x﹣2+x+3=2x+1,
在数轴上|x﹣2|+|x+3|的几何意义是:表示有理数x的点到﹣3及到2的距离之和,所以当﹣3≤x≤2时,它的最小值为5.
【点评】本题考查了数轴,绝对值的性质,读懂题目信息,理解数轴上两点间的距离的表示是解题的关键.注意分类思想在解题中的运用.
23.同一平面内1条直线把平面分成两个部分(或区域);2条直线最多可将平面分成几个部分?3条直线最多可将平面分成几个部分?4条直线最多可将平面分成几个部分?请分别画出图来.由此可知n条直线最多可将平面分成几个部分?
【分析】根据直线两两相交,每三条不交于同一点,可把平面分成最多部分,根据两条直线最多分成的部分比一条直线分成部分增加2,三条直线最多分成部分比两条直线最多分成部分增加三,以此类推,可得答案.
【解答】解:2条直线最多可将平面分成4个部分,如图:;
三条直线最多分成可将平面分成7个部分,如图:;
四条直线最多分成可将平面分成11个部分,如图:;
n条直线最多分成可将平面分成2+2+3+4+…+n=个部分.
【点评】本题考查了相交线,由图形得出规律是解题关键,规律1条直线分成两部分,两条直线增加2,三条直线再增加三,四条直线再增加四….
24.如图,直线AB,CD相交于点O,∠AOC=60°,∠1:∠2=1:2.
(1)求∠2的度数;
(2)若∠2与∠MOE互余,求∠MOB的度数.
【分析】(1)根据对顶角相等得到∠DOB=60°,根据已知求出∠2的度数;
(2)根据余角的概念求出∠MOE的度数,计算即可.
【解答】解:(1)∵∠DOB=∠AOC=60°,
∴∠1+∠2=60°,又∠1:∠2=1:2.
∴∠1=20°,∠2=40°;
(2)∵∠2与∠MOE互余,∠2=40°,
∴∠MOE=50°,又∠1=20°,
∴∠MOB=30°.
【点评】本题考查的是对顶角、邻补角的概念和余角补角的概念,掌握对顶角相等、如果两个角的和等于90°(直角),就说这两个角互为余角是解题的关键.
25.如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
【分析】(1)根据对顶角的性质可得∠AOC=∠BOD=36°,利用垂直定义可得∠COG=90°,然后再计算出∠AOG的度数即可;
(2)根据角平分线定义以及垂直定义可得∠COA=∠DOF,再根据对顶角相等可得∠DOF=∠COE,进而得出∠AOC=∠COE,即可得到OC平分∠AOE.
【解答】解:(1)∵AB、CD相交于点O,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=90°,
即∠AOC+∠AOG=90°,
∴∠AOG=90°﹣∠AOC=90°﹣36o=54o;
(2)OC是∠AOE的平分线.
∵OG是∠AOF的角平分线,
∴∠AOG=∠GOF,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠COA=∠DOF,
又∵∠DOF=∠COE,
∴∠AOC=∠COE,
∴OC平分∠AOE.
【点评】此题主要考查了角平分线的定义以及垂线,关键是掌握角平分线把角分成相等的两部分,注意理清图中角之间的关系.
26.如图,P是直线l外一点,A、B、C是直线l上的三点,且PB与l垂直,在从点P到点A、从点P到直线l的多条道路中,点P到点A的最短路线是 (3) ,点P到直线l的最短路线是 (4) (只填写序号即可).
【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;从直线外一点到这条直线上各点所连的线段中,垂线段最短.填空.
【解答】解:①因为两点之间线段最短,所以在连接PA的所有路线中,点P到点A的最短路线是(3),(1分)
②线段BP是点P到直线L的垂线段,根据垂线段最短可知,(1)~(5)中,PB最短,所以点P到直线l的最短路线是(4).(2分)
故答案是:(3)、(4).
【点评】本题主要考查了垂线段最短的性质和点到直线的距离的概念.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
