人教版七年级下册数学5.2.2平行线的判定课件(34张PPT)
文档属性
| 名称 | 人教版七年级下册数学5.2.2平行线的判定课件(34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 16:32:45 | ||
图片预览








文档简介
(共34张PPT)
课前两分钟候课要求:
准备好数学课本,练习本,直尺,铅笔,导纲和红黑双笔
平行线的判定
学习目标
1.掌握平行线的三种判定方法(重点)
2.灵活运用平行线的三种判定方法进行推理运算,并能用数字符号写出简单的推理过程(难点)
自学指导
请认真阅读书上第12页到第14页的内容,完成以下问题:
1.平行线的三种判定方法是什么?
2.回答14页的探究。
要求:自己独立思考 时间:5分钟
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
斜交
垂直
两条直线
位置关系
相交
平行
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线。
平行公理的推论
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
如果两条直线同平行于一条直线,那么两条直线平行。
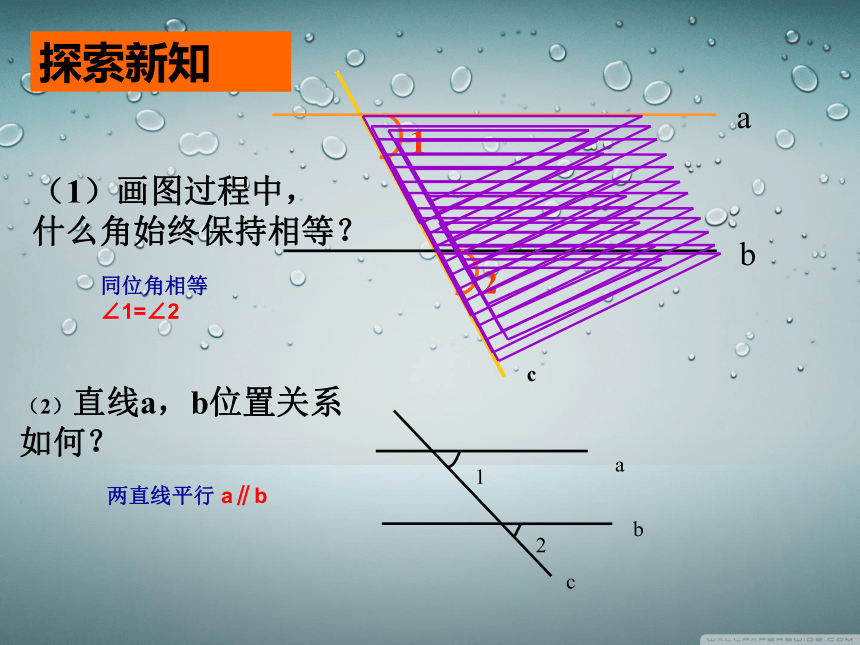
探索新知
b
2
1
a
c
1
2
a
b
c
(1)画图过程中,
什么角始终保持相等?
(2)直线a,b位置关系如何?
同位角相等∠1=∠2
两直线平行 a∥b
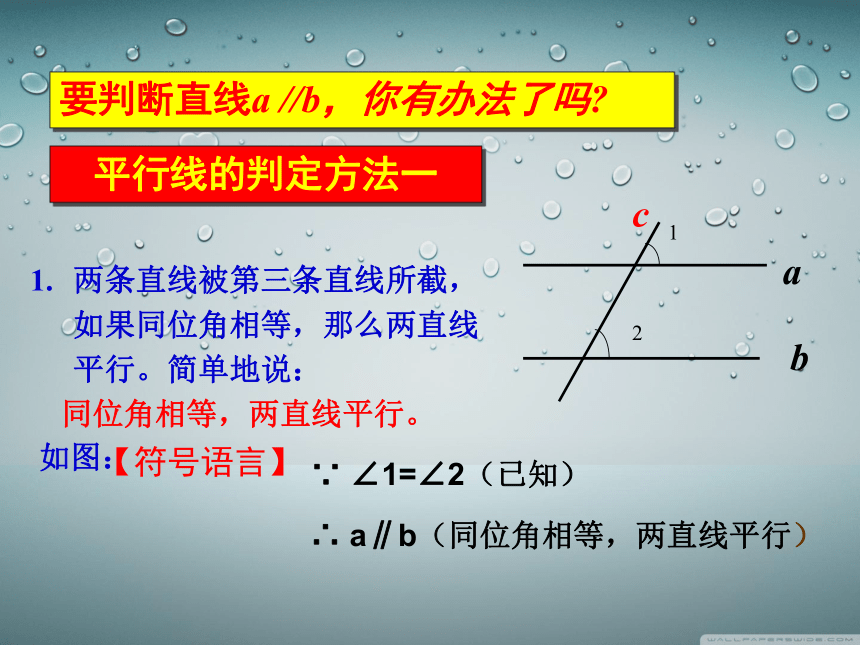
要判断直线a //b,你有办法了吗?
c
a
b
1
2
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
平行线的判定方法一
【符号语言】
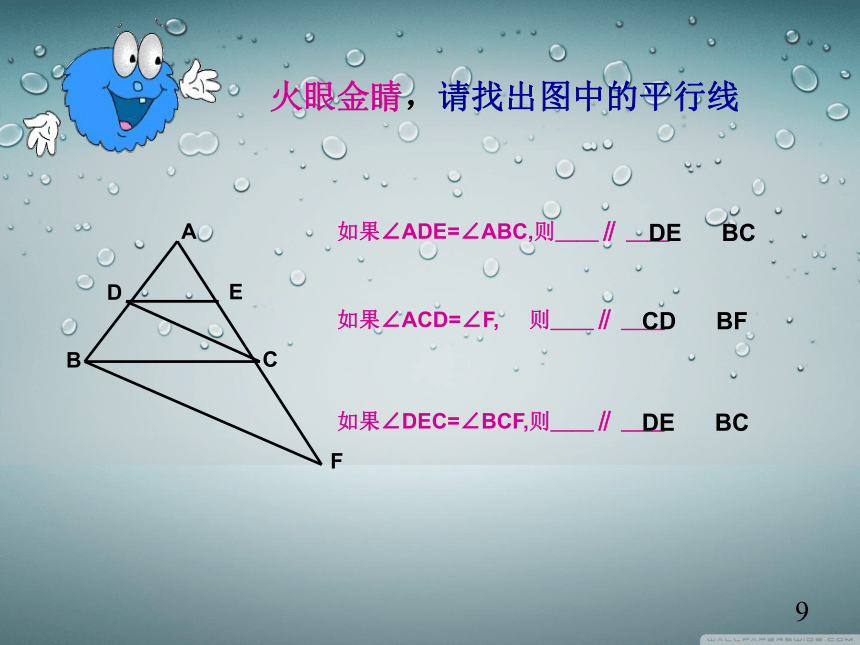
火眼金睛,请找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
DE BC
CD BF
DE BC
null
A
C
E
F
2
3
B
1
D
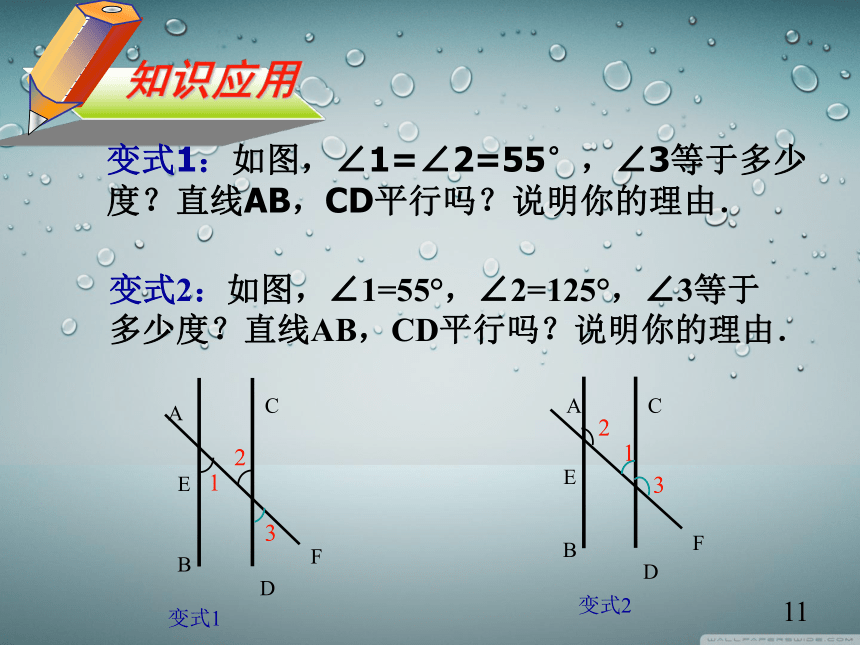
1.如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
知识应用
null
变式2:如图,∠1=55°,∠2=125°,∠3等于
多少度?直线AB,CD平行吗?说明你的理由.
知识应用
变式1:如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
E
F
2
C
A
3
B
1
D
变式1
C
A
E
F
2
3
B
1
D
变式2
null
简单说成: 内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号语言:如图
∵ ∠3=∠4(已知)
∴ a∥b
(内错角相等,两直线平行)
3
4
a
b
c
平行线的判定方法二
交流与发现:
如图,∠1与∠2互补,直线a与直线b平行吗?为什么?
由此,又得到怎样的方法去判定两条直线平行呢?
(第2题)
1
2
b
3
a
c
∴ AB∥CD (同旁内角互补,两直线平行)
同旁内角互补,两直线平行。
∵ ∠1+∠2=180 °
符号语言:
1
2
A
B
C
D
a
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
平行线的判定方法三
1.同位角相等,两直线平行。
3.同旁内角互补,两直线平行。
2.内错角相等,两直线平行。
平行线的判定方法
概括:
null
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补
两直线平行 ∵ . (已知)
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
null
1.已知:如图,a⊥c,b⊥c。求证:a∥b。
1
2
a
b
c
结论:在同一平面内,垂直于同一条直线的
两条直线互相平行。
拓展应用
2.如图,AD平分∠BAC, ∠1=∠3,
能推出AB∥CD吗?说明理由。
3.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,
那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
(第3题)
2
1
3
B
C
D
A
(第2题)
加油啊!推理就像走楼梯,要一步一步的逐层递进!
2
1
3
B
C
D
A
(第2题)
2.解:
∵AD平分∠BAC(已知)
∴∠1=∠2 (角平分线的定义)
又 ∵∠1= ∠3(已知)
∴ ∠2= ∠3 (等量代换)
∴ AB∥CD(内错角相等,两直线平行。)
A
E
B
C
D
N
M
(第3题)
∴ AB∥MN(内错角相等,两直线平行。)
3.解:
∵ ∠MCA= ∠ A(已知)
又 ∵∠ DEC= ∠ B(已知)
∴ AB∥DE(同位角相等,两直线平行。)
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行。)
注意哦!推理时可别忘了写上重要的理由哦!
1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )
A
B
C
D
E
1
2
3
AD BE
同位角相等,两直线平行.
BD CE
内错角相等,两直线平行.
AD BE
同旁内角互补,两直线平行.
∠D
内错角相等,两直线平行.
∠C
同旁内角互补,两直线平行.
自我测试
1.填空(认真思考)
null
2.已知∠3=45 °,∠1与∠2互余,试说明 ?
解:∵∠1=∠2(对顶角相等)
∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
null
3. 如图:已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
了解感知
完成导纲上了解感知部分
时间:5分钟
要求:自己独立思考
了解感知答案
1.AB ,CD内错角相等两直线平行
2.BCD,同旁内角互补两直线平行
3.3,2 内错角相等,两直线平行
4.∠ABC,同位角相等,两直线平行
A
B
D
C
完成深入学习练习
独立完成
时间:5分钟
Table of Contents
深入学习
A
B
D
C
展板
1,2组9号上班展示第三题
同组2号评板
Table of Contents
深入学习
深入学习答案
1D
2.C
3.解:∵∠1=50°
∴∠ECF=180°-∠1=130°
又∵CD平分∠ECF
∴∠ECD=∠DCF=
∵∠2=∠DCF=65°
∴CD∥FG(同位角相等,两直线平行)
时间:4分钟
完成迁移运用练习
独立完成
A
B
C
迁移运用
迁移应用答案
解:平行
理由:∵a⊥b,c⊥a
∴∠1=∠2=90°
∴b∥c(同位角相等,两直线平行)
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
课堂总结:平行线的判定
评激情小组
训
堂
练
CONTENTS
当
完成当堂训练
独立完成
时间:10分钟
谢谢!
课前两分钟候课要求:
准备好数学课本,练习本,直尺,铅笔,导纲和红黑双笔
平行线的判定
学习目标
1.掌握平行线的三种判定方法(重点)
2.灵活运用平行线的三种判定方法进行推理运算,并能用数字符号写出简单的推理过程(难点)
自学指导
请认真阅读书上第12页到第14页的内容,完成以下问题:
1.平行线的三种判定方法是什么?
2.回答14页的探究。
要求:自己独立思考 时间:5分钟
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢?
斜交
垂直
两条直线
位置关系
相交
平行
判定两条直线平行的方法有两种:
定义:在同一平面内,不相交的两条直线叫平行线。
平行公理的推论
同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?
如果两条直线同平行于一条直线,那么两条直线平行。
探索新知
b
2
1
a
c
1
2
a
b
c
(1)画图过程中,
什么角始终保持相等?
(2)直线a,b位置关系如何?
同位角相等∠1=∠2
两直线平行 a∥b
要判断直线a //b,你有办法了吗?
c
a
b
1
2
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
如图:
平行线的判定方法一
【符号语言】
火眼金睛,请找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
DE BC
CD BF
DE BC
null
A
C
E
F
2
3
B
1
D
1.如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
知识应用
null
变式2:如图,∠1=55°,∠2=125°,∠3等于
多少度?直线AB,CD平行吗?说明你的理由.
知识应用
变式1:如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由.
E
F
2
C
A
3
B
1
D
变式1
C
A
E
F
2
3
B
1
D
变式2
null
简单说成: 内错角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号语言:如图
∵ ∠3=∠4(已知)
∴ a∥b
(内错角相等,两直线平行)
3
4
a
b
c
平行线的判定方法二
交流与发现:
如图,∠1与∠2互补,直线a与直线b平行吗?为什么?
由此,又得到怎样的方法去判定两条直线平行呢?
(第2题)
1
2
b
3
a
c
∴ AB∥CD (同旁内角互补,两直线平行)
同旁内角互补,两直线平行。
∵ ∠1+∠2=180 °
符号语言:
1
2
A
B
C
D
a
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
平行线的判定方法三
1.同位角相等,两直线平行。
3.同旁内角互补,两直线平行。
2.内错角相等,两直线平行。
平行线的判定方法
概括:
null
判定两条直线平行的方法
文字叙述 符号语言 图形
相等
两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补
两直线平行 ∵ . (已知)
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
3
4
null
1.已知:如图,a⊥c,b⊥c。求证:a∥b。
1
2
a
b
c
结论:在同一平面内,垂直于同一条直线的
两条直线互相平行。
拓展应用
2.如图,AD平分∠BAC, ∠1=∠3,
能推出AB∥CD吗?说明理由。
3.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,
那么DE∥MN吗?为什么?
A
E
B
C
D
N
M
(第3题)
2
1
3
B
C
D
A
(第2题)
加油啊!推理就像走楼梯,要一步一步的逐层递进!
2
1
3
B
C
D
A
(第2题)
2.解:
∵AD平分∠BAC(已知)
∴∠1=∠2 (角平分线的定义)
又 ∵∠1= ∠3(已知)
∴ ∠2= ∠3 (等量代换)
∴ AB∥CD(内错角相等,两直线平行。)
A
E
B
C
D
N
M
(第3题)
∴ AB∥MN(内错角相等,两直线平行。)
3.解:
∵ ∠MCA= ∠ A(已知)
又 ∵∠ DEC= ∠ B(已知)
∴ AB∥DE(同位角相等,两直线平行。)
∴ DE∥MN(如果两条直线都和第三条直线平行,那么这两条直线也互相平行。)
注意哦!推理时可别忘了写上重要的理由哦!
1.如果∠A=∠3,那么 ∥ ,
( )
2.如果∠2=∠E,那么 ∥ ,
( )
3.如果∠A+∠ABE=1800,那么 ∥ ,
( )
4.如果∠2= ,那么DA∥EB
( )
5.如果∠DBC+ =1800,那么DB∥EC
( )
A
B
C
D
E
1
2
3
AD BE
同位角相等,两直线平行.
BD CE
内错角相等,两直线平行.
AD BE
同旁内角互补,两直线平行.
∠D
内错角相等,两直线平行.
∠C
同旁内角互补,两直线平行.
自我测试
1.填空(认真思考)
null
2.已知∠3=45 °,∠1与∠2互余,试说明 ?
解:∵∠1=∠2(对顶角相等)
∠1+∠2=90°(已知)
∴∠1=∠2=45°
∵ ∠3=45°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
AB//CD
null
3. 如图:已知 ∠1=75o , ∠2 =105o
问:AB与CD平行吗?为什么?
A
C
1
4
2
3
B
D
5
了解感知
完成导纲上了解感知部分
时间:5分钟
要求:自己独立思考
了解感知答案
1.AB ,CD内错角相等两直线平行
2.BCD,同旁内角互补两直线平行
3.3,2 内错角相等,两直线平行
4.∠ABC,同位角相等,两直线平行
A
B
D
C
完成深入学习练习
独立完成
时间:5分钟
Table of Contents
深入学习
A
B
D
C
展板
1,2组9号上班展示第三题
同组2号评板
Table of Contents
深入学习
深入学习答案
1D
2.C
3.解:∵∠1=50°
∴∠ECF=180°-∠1=130°
又∵CD平分∠ECF
∴∠ECD=∠DCF=
∵∠2=∠DCF=65°
∴CD∥FG(同位角相等,两直线平行)
时间:4分钟
完成迁移运用练习
独立完成
A
B
C
迁移运用
迁移应用答案
解:平行
理由:∵a⊥b,c⊥a
∴∠1=∠2=90°
∴b∥c(同位角相等,两直线平行)
判定方法1 同位角相等,两直线平行.
判定方法2 内错角相等,两直线平行.
判定方法3 同旁内角互补,两直线平行.
课堂总结:平行线的判定
评激情小组
训
堂
练
CONTENTS
当
完成当堂训练
独立完成
时间:10分钟
谢谢!
