人教版八年级数学下册19.2.2一次函数(3)课件(25张PPT)
文档属性
| 名称 | 人教版八年级数学下册19.2.2一次函数(3)课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 23:29:26 | ||
图片预览





文档简介
(共25张PPT)
19.2.2 一次函数(3)
学习目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次
函数模型解决现实生活中的问题,体会一次函数
的应用价值.
学习重点:
用待定系数法求一次函数解析式初步了解分段函数
学习难点:
能通过函数解决简单的实际问题.
一导学
1、正比例函数的解析式为:
当x=0时,y= 当x=1时,y=
所以,它的图象必经过点( )( )
y= kx,(k≠0)
2、一次函数的解析式为:
y=kx+b(k≠0)
0
b
0 , b
当x=0时,y= 当y=0时,x=
或当x=1时,y= 所以,它的图象必经过点( )和点( )或( )
0,0
1,k
1,k+b
K+b
k
回顾旧知
3、正比例函数的图象是什么? 如何画出正比例函数的图象?
(直线)
(描两点并画出直线)
4、一次函数的图象是什么? 如何画出一次函数的图象?
(直线)
(描两点并画出直线)
(0,0)(1,k)
(0 ,b)(1 ,k+b)
或 以确定特殊自变量0、1来定两点
以坐标轴上坐标特点来确定两点
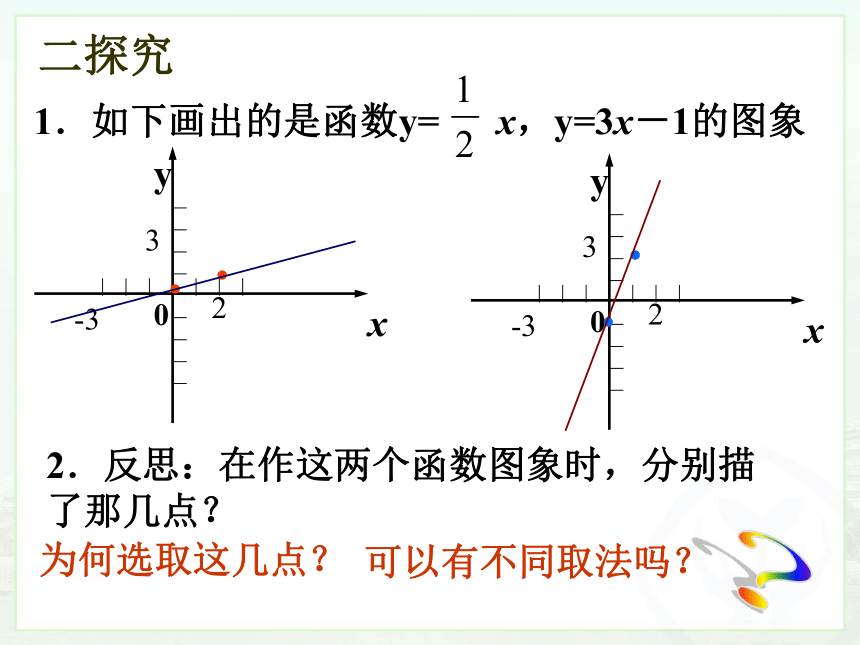
2.反思:在作这两个函数图象时,分别描 了那几点?
为何选取这几点?
可以有不同取法吗?
.
.
.
.
二探究
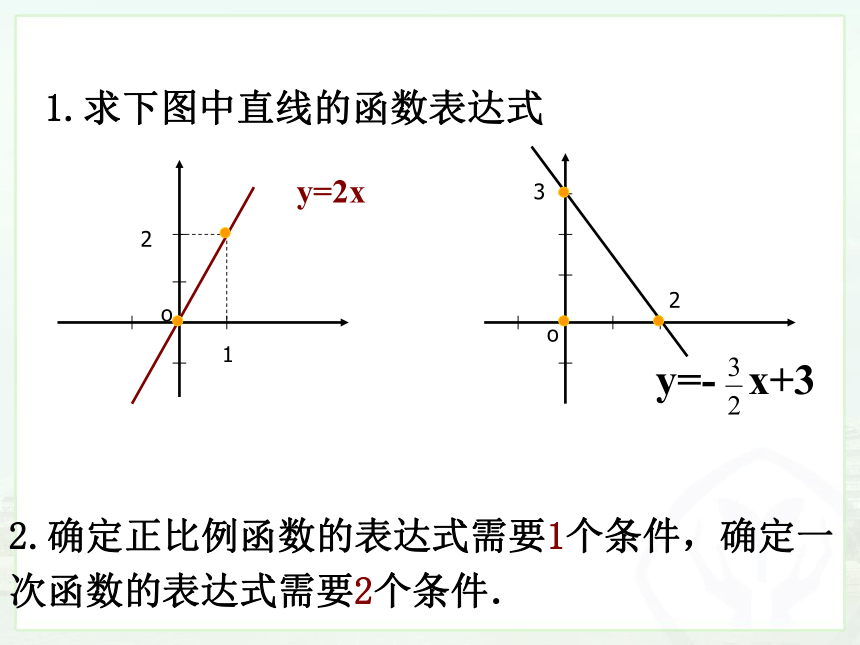
1.求下图中直线的函数表达式
2.确定正比例函数的表达式需要1个条件,确定一次函数的表达式需要2个条件.
y=2x
y=- x+3
1
2
3
2
o
o
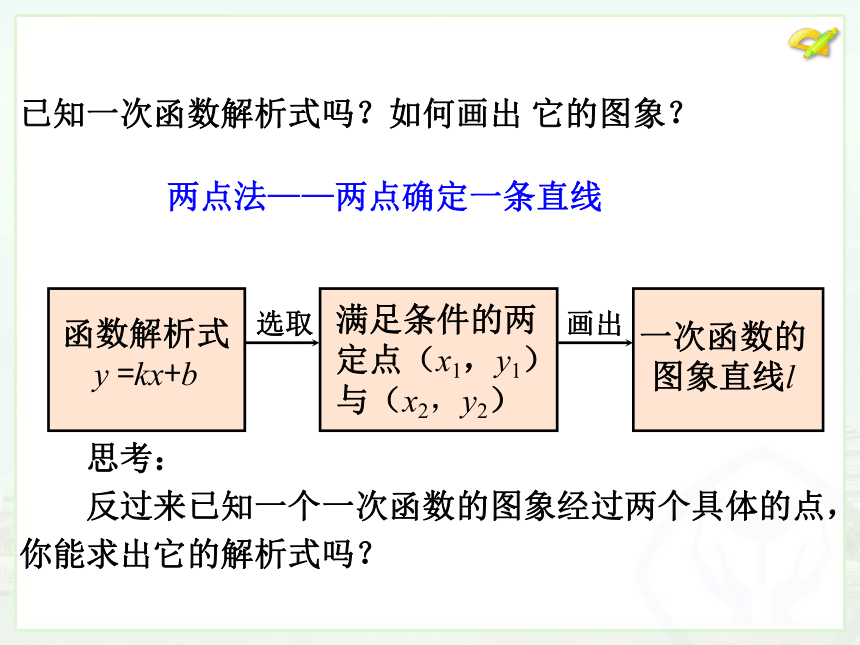
已知一次函数解析式吗?如何画出 它的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
例1 已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点(3,5)与(-4,-9).
∴这个一次函数的解析式为y=2x-1
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
例题讲解
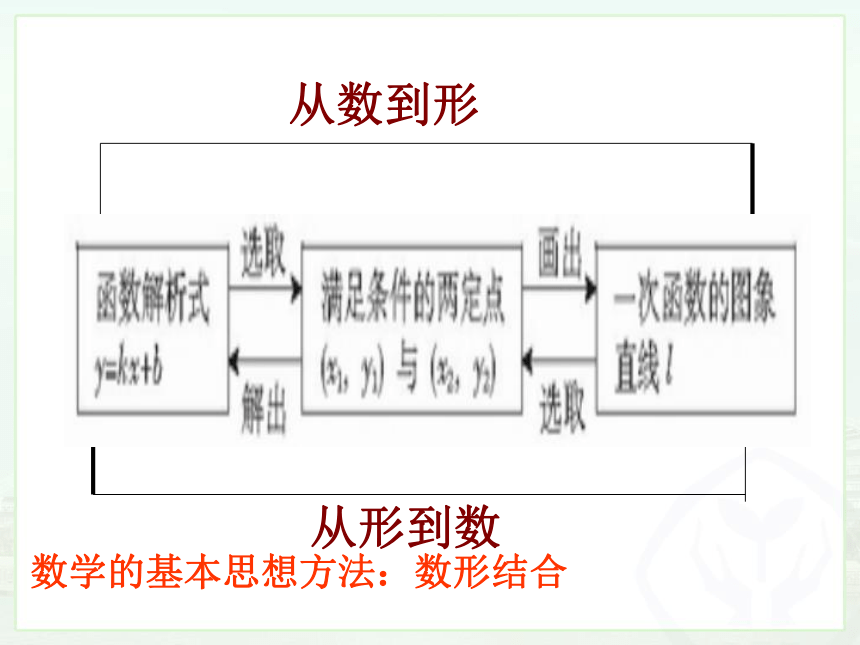
从数到形
从形到数
数学的基本思想方法:数形结合
求函数解析式的一般步骤是怎样的呢?
可归纳为:“一设、二列、三解、四还原”
一设:设出函数解析式的一般形式y=kx+b;
二列 :将已知点的坐标代入函数解析式,列出关于k、b的二元一次方程组;
三解:解这个方程组,求出k、b的值;
四还原:把求得的k、b的值代入y=kx+b,写出函
数解析式.
例2 “黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表.
2.5
5
7.5
10
12.5
15
17.5
20
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x千克,付款金额为y元.
当x>2时,
y=4(x-2)+10=4x+2.
当0≤x≤2时,
y=5x;
函数图象如图所示:
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每个家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设某个家庭用水量为x立方米时,应交水费y元. ①分别求出0≤x≤20和x>20时,y与x的函数解析式.
②小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
月份 四月份 五月份 六月份
交费金额 30元 34元 42.6元
我们称此类函数为分段函数.
开始时引入图象所表示的是分段函数吗?你能写出它的解析式吗?说说你的做法.
s=6t;
0≤t≤2时,
2<t≤4时,
s=12;
4<t≤6时,
s=-6t+12.
1.已知一次函数y=kx+b的图象如图所示,求函数表达式.
[分析] 从图象上可以看出,它与x轴交于点(-1,0),与y轴交于点(0,-3),代入关系式中,求出k为即可.
解方程组得:
∴这个一次函数的表达式为y=-3x-3.
解:由图象可知,图象经过点(-1,0)和(0,-3)两点,代入到y=kx+b中,得
三检测
2.判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
[分析] 由于两点确定一条直线,故选取其中两点,求经过
这两点的函数表达式,再把第三个点的坐标代入表达式中,
若成立,说明在此直线上;若不成立,说明不在此直线上.
3.在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧,当不挂物体时,弹簧长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
4.已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
5.某地区电话的月租费为25元,可打50次电话(每次3分钟),超过50次后,每次0.2元,
(1)写出每月电话费y(元)与通话次数x(x 50)的函数关系式;
(2)求出月通话150次的电话费;
(3)如果某月通话费53.6元,求该月的通话次数。
6.已知y-100与x成正比例,且当x=10时,y=600.
(1)求y关于x的函数解析式.
(2)当-300<y≤400时, 自变量x的取值范围。
解:
把x=10时,y=600代入y-100=kx,得
(1)设这个正比例函数解析式为 y-100=kx
解得
k=50
∴y-100=50x
600-100=10k
即y=50x+100
(2)当-300<y≤400时, -300<50x+100 ≤400
∴自变量x的取值范围为-8<x≤6
7.小芳以200米/分速度起跑后,先匀加速跑5分,每分提高速度20米/分,又匀速跑10分。试写出这段时间里她的跑步速度y(单位:米/分)随跑步时间x(单位:分)变化的函数关系式,并画出函数图象。
(1)跑步速度y与跑步时间x的函数关系式为:
(2)画函数y=20x+200(0≤x ≤ 5)图象
列表:
描点:
连线:
画函数y=300(5<x≤15)图象
200
300
(1)当0≤x≤5时,y=20x+200
当5<x≤15时,y=300
解:
(1)本节课,我们研究了什么,得到了哪些成果?
(2)用待定系数法求一次函数解析式的解题步骤是
什么?
(3)我们是如何建立一次函数模型解决实际问题的?
(4)书写分段函数的解析式时要注意什么?
1.课堂小结
四 拓展
1.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
0.9元/度
0.5元/度
O
2.知识延伸
2.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药
(1)服药后____时,血液中含药量最高,达到每毫升_______毫克。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时,y与x之间的函数关系式是_____。
(4)当x≥2时,y与x之间的函数关系式是_________。
(5)如果每毫升血液中含药量3毫克
或3毫克以上时,治疗疾病最有效,
那么这个有效时间是___ 小时。.
2
6
3
y=3x
y=-x+8
4
作业:教科书第99~100页习题19.2第7,11,
14,15题.
课后作业
19.2.2 一次函数(3)
学习目标:
1.学会用待定系数法求一次函数解析式;
2.了解分段函数的表示及其图象;能初步应用一次
函数模型解决现实生活中的问题,体会一次函数
的应用价值.
学习重点:
用待定系数法求一次函数解析式初步了解分段函数
学习难点:
能通过函数解决简单的实际问题.
一导学
1、正比例函数的解析式为:
当x=0时,y= 当x=1时,y=
所以,它的图象必经过点( )( )
y= kx,(k≠0)
2、一次函数的解析式为:
y=kx+b(k≠0)
0
b
0 , b
当x=0时,y= 当y=0时,x=
或当x=1时,y= 所以,它的图象必经过点( )和点( )或( )
0,0
1,k
1,k+b
K+b
k
回顾旧知
3、正比例函数的图象是什么? 如何画出正比例函数的图象?
(直线)
(描两点并画出直线)
4、一次函数的图象是什么? 如何画出一次函数的图象?
(直线)
(描两点并画出直线)
(0,0)(1,k)
(0 ,b)(1 ,k+b)
或 以确定特殊自变量0、1来定两点
以坐标轴上坐标特点来确定两点
2.反思:在作这两个函数图象时,分别描 了那几点?
为何选取这几点?
可以有不同取法吗?
.
.
.
.
二探究
1.求下图中直线的函数表达式
2.确定正比例函数的表达式需要1个条件,确定一次函数的表达式需要2个条件.
y=2x
y=- x+3
1
2
3
2
o
o
已知一次函数解析式吗?如何画出 它的图象?
思考:
反过来已知一个一次函数的图象经过两个具体的点,
你能求出它的解析式吗?
两点法——两点确定一条直线
例1 已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
∵y=kx+b的图象过点(3,5)与(-4,-9).
∴这个一次函数的解析式为y=2x-1
像这样先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
例题讲解
从数到形
从形到数
数学的基本思想方法:数形结合
求函数解析式的一般步骤是怎样的呢?
可归纳为:“一设、二列、三解、四还原”
一设:设出函数解析式的一般形式y=kx+b;
二列 :将已知点的坐标代入函数解析式,列出关于k、b的二元一次方程组;
三解:解这个方程组,求出k、b的值;
四还原:把求得的k、b的值代入y=kx+b,写出函
数解析式.
例2 “黄金1号”玉米种子的价格为5元/kg. 如果一次购买2kg以上的种子,超过2kg部分的种子价格打8折.
(1)填写下表.
2.5
5
7.5
10
12.5
15
17.5
20
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
解:设购买量为x千克,付款金额为y元.
当x>2时,
y=4(x-2)+10=4x+2.
当0≤x≤2时,
y=5x;
函数图象如图所示:
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每个家庭的水费,月用水量不超过20立方米时,按2元/立方米计费;月用水量超过20立方米时,其中的20立方米仍按2元/立方米收费,超过部分按2.6元/立方米计费.设某个家庭用水量为x立方米时,应交水费y元. ①分别求出0≤x≤20和x>20时,y与x的函数解析式.
②小明家第二季度交纳水费的情况如下:
小明家这个季度共用水多少立方米?
月份 四月份 五月份 六月份
交费金额 30元 34元 42.6元
我们称此类函数为分段函数.
开始时引入图象所表示的是分段函数吗?你能写出它的解析式吗?说说你的做法.
s=6t;
0≤t≤2时,
2<t≤4时,
s=12;
4<t≤6时,
s=-6t+12.
1.已知一次函数y=kx+b的图象如图所示,求函数表达式.
[分析] 从图象上可以看出,它与x轴交于点(-1,0),与y轴交于点(0,-3),代入关系式中,求出k为即可.
解方程组得:
∴这个一次函数的表达式为y=-3x-3.
解:由图象可知,图象经过点(-1,0)和(0,-3)两点,代入到y=kx+b中,得
三检测
2.判断三点A(3,1),B(0,-2),C(4,2)是否在同一条直线上.
∴过A,B两点的直线的表达式为y=x-2.
∵当x=4时,y=4-2=2.
∴点C(4,2)在直线y=x-2上.
∴三点A(3,1), B(0,-2),C(4,2)在同一条直线上.
[分析] 由于两点确定一条直线,故选取其中两点,求经过
这两点的函数表达式,再把第三个点的坐标代入表达式中,
若成立,说明在此直线上;若不成立,说明不在此直线上.
3.在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧,当不挂物体时,弹簧长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
4.已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。
5.某地区电话的月租费为25元,可打50次电话(每次3分钟),超过50次后,每次0.2元,
(1)写出每月电话费y(元)与通话次数x(x 50)的函数关系式;
(2)求出月通话150次的电话费;
(3)如果某月通话费53.6元,求该月的通话次数。
6.已知y-100与x成正比例,且当x=10时,y=600.
(1)求y关于x的函数解析式.
(2)当-300<y≤400时, 自变量x的取值范围。
解:
把x=10时,y=600代入y-100=kx,得
(1)设这个正比例函数解析式为 y-100=kx
解得
k=50
∴y-100=50x
600-100=10k
即y=50x+100
(2)当-300<y≤400时, -300<50x+100 ≤400
∴自变量x的取值范围为-8<x≤6
7.小芳以200米/分速度起跑后,先匀加速跑5分,每分提高速度20米/分,又匀速跑10分。试写出这段时间里她的跑步速度y(单位:米/分)随跑步时间x(单位:分)变化的函数关系式,并画出函数图象。
(1)跑步速度y与跑步时间x的函数关系式为:
(2)画函数y=20x+200(0≤x ≤ 5)图象
列表:
描点:
连线:
画函数y=300(5<x≤15)图象
200
300
(1)当0≤x≤5时,y=20x+200
当5<x≤15时,y=300
解:
(1)本节课,我们研究了什么,得到了哪些成果?
(2)用待定系数法求一次函数解析式的解题步骤是
什么?
(3)我们是如何建立一次函数模型解决实际问题的?
(4)书写分段函数的解析式时要注意什么?
1.课堂小结
四 拓展
1.为缓解用电紧张,某电力公司特制定了新的用电收费标准,每月用电量x(度)与应付电费y(元)的关系如图所示.
(1)根据图象,请分别求出当0≤x≤50和x>50时,y与x的函数解析式.
(2)请回答:
当每月用电量不超过50度时,收费标准是 ;
当每月用电量超过50度时,收费标准是 .
0.9元/度
0.5元/度
O
2.知识延伸
2.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药
(1)服药后____时,血液中含药量最高,达到每毫升_______毫克。
(2)服药5时,血液中含药量为每毫升____毫克。
(3)当x≤2时,y与x之间的函数关系式是_____。
(4)当x≥2时,y与x之间的函数关系式是_________。
(5)如果每毫升血液中含药量3毫克
或3毫克以上时,治疗疾病最有效,
那么这个有效时间是___ 小时。.
2
6
3
y=3x
y=-x+8
4
作业:教科书第99~100页习题19.2第7,11,
14,15题.
课后作业
