2019-2020学年沪教版上海市徐汇区西南模范中学八年级第一学期(上)期中数学试卷 解析版
文档属性
| 名称 | 2019-2020学年沪教版上海市徐汇区西南模范中学八年级第一学期(上)期中数学试卷 解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-19 16:29:54 | ||
图片预览



文档简介
2019-2020学年上海市徐汇区西南模范中学八年级(上)
期中数学试卷
一、选择题(本大题共6题)
1.在下列方程中,一元二次方程的个数是
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
2.方程的根为
A. B. C., D.,
3.已知函数中随的增大而增大,那么它和函数在同一直角坐标系内的大致图象可能是
A. B.
C. D.
4.到一个三角形三个顶点的距离都相等的点是这个三角形
A.三条中线的交点 B.三条高的交点
C.三边中垂线的交点 D.三条角平分线的交点
5.下列说法错误的是
A.到点距离等于的点的轨迹是以点为圆心,半径长为的圆
B.等腰的底边固定,顶点的轨迹是线段的垂直平分线
C.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
D.到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线
6.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
二、填空题(本大题共12题,每题2分,满分24分)
7.函数的定义域是 .
8.方程的解为 .
9.方程的根是 .
10.在实数范围内因式分解: .
11.已知正比例函数的图象经过第一、三象限,则的取值范围是 .
12.已知点,和,都在反比例函数的图象上,若,则、的大小关系是 .
13.命题“平行于同一直线的两直线平行”的逆命题是: .
14.某企业生产某种产品,今年产量为200件,计划通过技术革新,三年(包括今年)的产量达到1400件,若明后两年的产量平均增长率相同为,可以得到方程: .
15.在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于,,作直线,交于点,连接.如果,,那么 .
16.如图,已知在中,是边上的高,平分,交于点,,,则的面积等于 .
17.如图,中,平分,的中垂线交于点,交于点,连接,.若为等腰三角形,则的度数为 .
18.如图,在中,,的平分线与的外角平分线交于点,则的度数为 .(用含的式子表示)
三、简答题(本大题共4题)
19.解方程:
20.用配方法解方程:
21.解方程:
22.已知:、点及线段(如图).求作:点,使得点到和的距离相等,且.(要求尺规作图,保留作图痕迹,不必写作法和证明)
四、解答题(本大题共4题)
23.已知关于的一元二次方程有两个不相等的实数根,求的取值范围.
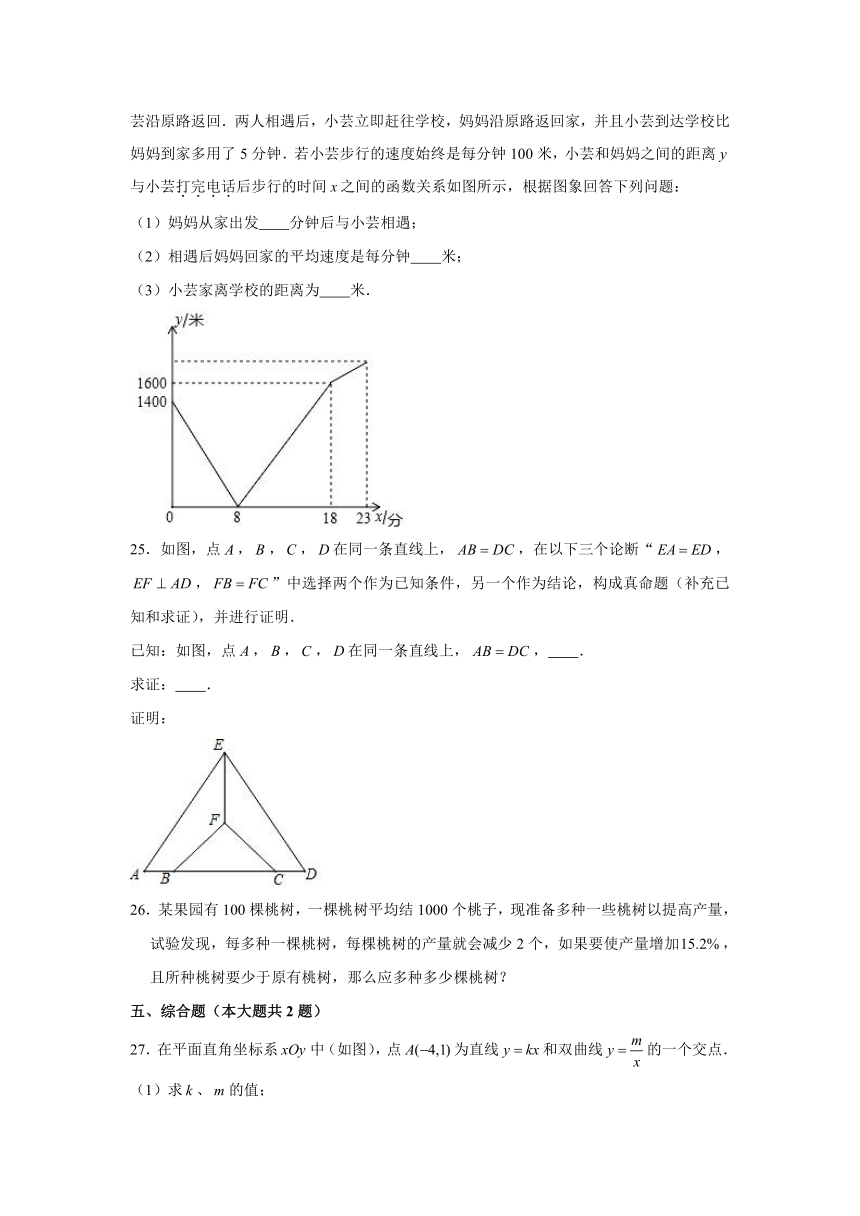
24.小芸家与学校之间是一条笔直的公路,小芸从家步行前往学校的途中发现忘记带阅读分享要用的盘,便停下给妈妈打电话,妈妈接到电话后,带上盘马上赶往学校,同时小芸沿原路返回.两人相遇后,小芸立即赶往学校,妈妈沿原路返回家,并且小芸到达学校比妈妈到家多用了5分钟.若小芸步行的速度始终是每分钟100米,小芸和妈妈之间的距离与小芸打完电话后步行的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)妈妈从家出发 分钟后与小芸相遇;
(2)相遇后妈妈回家的平均速度是每分钟 米;
(3)小芸家离学校的距离为 米.
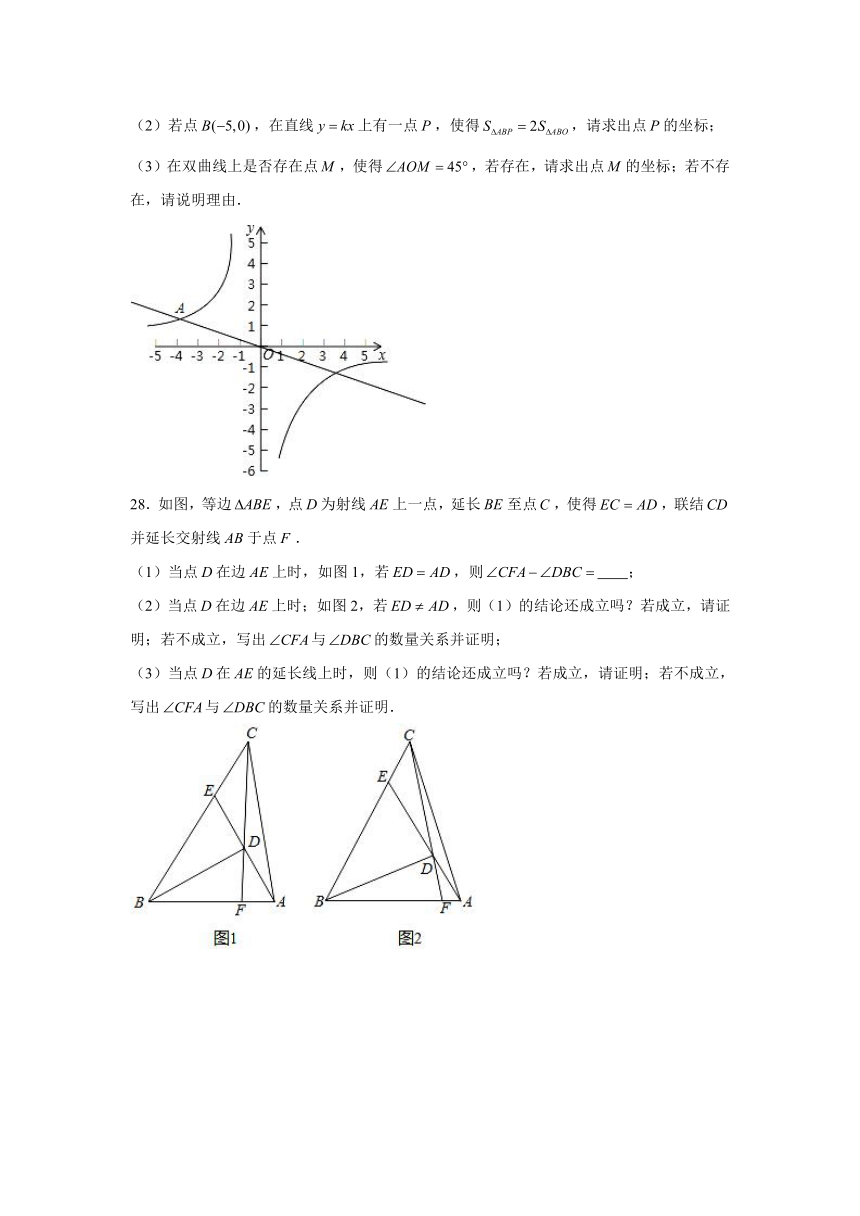
25.如图,点,,,在同一条直线上,,在以下三个论断“,,”中选择两个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点,,,在同一条直线上,, .
求证: .
证明:
26.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加,且所种桃树要少于原有桃树,那么应多种多少棵桃树?
五、综合题(本大题共2题)
27.在平面直角坐标系中(如图),点为直线和双曲线的一个交点.
(1)求、的值;
(2)若点,在直线上有一点,使得,请求出点的坐标;
(3)在双曲线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
28.如图,等边,点为射线上一点,延长至点,使得,联结并延长交射线于点.
(1)当点在边上时,如图1,若,则 ;
(2)当点在边上时;如图2,若,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明;
(3)当点在的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明.
2019-2020学年上海市徐汇区西南模范中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.在下列方程中,一元二次方程的个数是
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
【分析】本题根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【解答】解:①,是一元二次方程,故本小题正确;
②,时是一元二次方程,故本小题错误;
③,整理后不是一元二次方程,故本小题错误;
④,是分式方程,不是一元二次方程,故本小题错误.
故选:.
2.方程的根为
A. B. C., D.,
【分析】两边直接开平方法求解可得.
【解答】解:,
或,
解得:或,
故选:.
3.已知函数中随的增大而增大,那么它和函数在同一直角坐标系内的大致图象可能是
A. B.
C. D.
【分析】先根据正比例函数的性质判断出的符号,再根据反比例函数的性质利用排除法求解即可.
【解答】解:函数中随的增大而增大,
,
函数的图象经过一、三象限,故可排除、;
,
,
函数的图象在二、四象限,故错误,正确.
故选:.
4.到一个三角形三个顶点的距离都相等的点是这个三角形
A.三条中线的交点 B.三条高的交点
C.三边中垂线的交点 D.三条角平分线的交点
【分析】根据线段的操作票个方向的性质即可判断.
【解答】解:三角形的三边的中垂线到三个顶点距离相等,
故选:.
5.下列说法错误的是
A.到点距离等于的点的轨迹是以点为圆心,半径长为的圆
B.等腰的底边固定,顶点的轨迹是线段的垂直平分线
C.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
D.到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线
【分析】利用圆的定义,线段垂直平分线的性质,等腰三角形的性质,角平分线的性质依次判断即可求解.
【解答】解:、到点距离等于的点的轨迹是以点为圆心,半径为的圆,故选项不符合题意;
、等腰的底边固定,顶点的轨迹是线段的垂直平分线(线段中点除外),故选项符合题意;
、在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线,故选项不符合题意;
、到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线,故选项不符合题意;
故选:.
6.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
【分析】根据三角形内角和定理可求,根据垂直平分线性质,,,则,,从而可得,即可得到,即可得解.
【解答】解:,
,
的垂直平分线交边于点,的垂直平分线交边于点,
,,
,,
,
,
.
故选:.
二、填空题(本大题共12题,每题2分,满分24分)
7.函数的定义域是 .
【分析】当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零,依此即可求解.
【解答】解:依题意有,
解得.
故答案为:.
8.方程的解为 .
【分析】根据配方法可以解答本题.
【解答】解:,
,
所以,,
故答案为.
9.方程的根是 或 .
【分析】利用因式分解法求解可得.
【解答】解:,
,
则,
或,
解得或,
故答案为:或.
10.在实数范围内因式分解: .
【分析】利用求根公式求得关于的一元二次方程的两根,然后利用公式法进行因式分解.
【解答】解:解关于的一元二次方程得到:,.
所以.
故答案是:.
11.已知正比例函数的图象经过第一、三象限,则的取值范围是 .
【分析】先根据正比例函数的图象经过第一、三象限列出关于的不等式,求出的取值范围即可.
【解答】解:正比例函数的图象经过第一、三象限,
,
.
故答案为:.
12.已知点,和,都在反比例函数的图象上,若,则、的大小关系是 .
【分析】反比例函数的图象位于一、三象限,在每个象限内,随的增大而减小,又,可得到点,和,在第三象限图象上的两点,可得
【解答】解:,
在每个象限内,随的增大而减小,
又,
可得,
故答案为:
13.命题“平行于同一直线的两直线平行”的逆命题是: “如果两直线平行于同一直线,那么这两条直线平行” .
【分析】把一个命题的条件和结论互换就得到它的逆命题.
【解答】解:命题“平行于同一直线的两直线平行”的逆命题是:“如果两直线平行于同一直线,那么这两条直线平行”,
故答案为:“如果两直线平行于同一直线,那么这两条直线平行”.
14.某企业生产某种产品,今年产量为200件,计划通过技术革新,三年(包括今年)的产量达到1400件,若明后两年的产量平均增长率相同为,可以得到方程: .
【分析】设明后两年的产量平均增长率为,根据三年(包括今年)的产量达到1400件,即可得出关于的一元二次方程,此题得解.
【解答】解:设明后两年的产量平均增长率为,
依题意,得:.
故答案为:.
15.在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于,,作直线,交于点,连接.如果,,那么 3 .
【分析】直接利用基本作图方法得出垂直平分,进而得出答案.
【解答】解:由作图步骤可得:垂直平分,则,
,,
.
故答案为:3.
16.如图,已知在中,是边上的高,平分,交于点,,,则的面积等于 5 .
【分析】过作于点,由角平分线的性质可求得,则可求得的面积.
【解答】解:
过作于点,
是边上的高,平分,
,
,
故答案为:5.
17.如图,中,平分,的中垂线交于点,交于点,连接,.若为等腰三角形,则的度数为 或或 .
【分析】根据角平分线的定义求出的度数,根据线段垂直平分线的性质得到,根据等腰三角形的性质得到答案.
【解答】解:平分,
,
是的中垂线,
,
,
,
为等腰三角形,
当,
,
,
,
当,
,
,
,
当,
,
,
综上所述,的度数为或或,
故答案为:或或.
18.如图,在中,,的平分线与的外角平分线交于点,则的度数为 .(用含的式子表示)
【分析】首先证明也是的外角的平分线,根据平角的定义和角平分线的定义求得,的度数,最后根据三角形的内角和定理即可求得.
【解答】解:在的平分线上,
点到的距离等于到的距离,
在的外角的平分线上,
点到的距离等于到的距离,
点到的距离等于到的距离,
是的外角的平分线,
,
,
故答案为.
三、简答题(本大题共4题,每题5分,满分20分)
19.解方程:
【分析】先把方程化为一般式,再计算判别式的值,然后利用求根公式求解.
【解答】解:,
,
,,
△,
,
所以,.
20.用配方法解方程:
【分析】方程二次项系数化为1,常数项移到右边,利用完全平方公式配方后,开方即可求出解.
【解答】解:方程整理得:,
配方得:,即,
或,
,.
21.解方程:
【分析】先将方程化为一般形式,确定,,的值,然后代入求根公式进行计算即可.
【解答】解:,
整理得:,
,,,△,
.
即,.
22.已知:、点及线段(如图).求作:点,使得点到和的距离相等,且.(要求尺规作图,保留作图痕迹,不必写作法和证明)
【分析】根据角平分线上的点到角的两边的距离相等可得点在的平分线上,然后再以点为圆心,以的长度为半径画弧,与的平分线相交于一点,交点就是所求的点.
【解答】解:
所以两个位置的点就是所要求作的点.
每作对一个点得2分,共4分;结论2分.
四、解答题(本大题共4题,每题6分,满分24分)
23.已知关于的一元二次方程有两个不相等的实数根,求的取值范围.
【分析】由方程有两个不相等的实数根,根据根的判别式可得到关于的不等式,可求得的取值范围.
【解答】解:方程有两个不相等的实数根,
△且且即且且,
解得且.
故的取值范围是且.
24.小芸家与学校之间是一条笔直的公路,小芸从家步行前往学校的途中发现忘记带阅读分享要用的盘,便停下给妈妈打电话,妈妈接到电话后,带上盘马上赶往学校,同时小芸沿原路返回.两人相遇后,小芸立即赶往学校,妈妈沿原路返回家,并且小芸到达学校比妈妈到家多用了5分钟.若小芸步行的速度始终是每分钟100米,小芸和妈妈之间的距离与小芸打完电话后步行的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)妈妈从家出发 8 分钟后与小芸相遇;
(2)相遇后妈妈回家的平均速度是每分钟 米;
(3)小芸家离学校的距离为 米.
【分析】(1)根据函数图象中的数据可知妈妈从家出发几分钟后与小芸相遇;
(2)根据函数图象中的数据可以求得相遇后妈妈回家的平均速度;
(3)根据函数图象中的数据可以求得小芸家离学校的距离.
【解答】解:(1)由图象可得,
妈妈从家出发8分钟后与小芸相遇,
故答案为:8;
(2)相遇后妈妈回家的平均速度是每分钟:(米,
故答案为:60;
(3)小芸家离学校的距离为:(米,
故答案为:2100.
25.如图,点,,,在同一条直线上,,在以下三个论断“,,”中选择两个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点,,,在同一条直线上,, , .
求证: .
证明:
【分析】根据题意写出已知、求证,根据线段垂直平分线的判定定理证明.
【解答】已知:如图,点,,,在同一条直线上,,,,
求证:,
证明:,
点在线段的垂直平分线上,
点在线段的垂直平分线上,
,
点在线段的垂直平分线上,
,
故答案为:,;.
26.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加,且所种桃树要少于原有桃树,那么应多种多少棵桃树?
【分析】每多种一棵桃树,每棵桃树的产量就会减少2个,所以多种棵树每棵桃树的产量就会减少个(即是平均产个),桃树的总共有棵,所以总产量是个.要使产量增加,达到个.
【解答】解:设应多种棵桃树,则由题意可得:
整理,得:,
即,
解得:,
因为所种桃树要少于原有桃树,
所以不符合题意,应舍去,取,
答:应多种20棵桃树.
五、综合题(本大题共2题,每题10分,满分20分)
27.在平面直角坐标系中(如图),点为直线和双曲线的一个交点.
(1)求、的值;
(2)若点,在直线上有一点,使得,请求出点的坐标;
(3)在双曲线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法即可解决问题.
(2)如图1中,设直线与反比例函数的另一个交点为.由对称性可知:,推出当点与重合时,,此时.当点在的延长线上时,时,,再利用中点坐标公式求解即可.
(3)如图2中,将绕点顺时针旋转得到,则,取的中点,作直线在第二象限交反比例函数于.此时,求出直线的解析式,再构建方程组确定点的坐标.
【解答】解:(1)点在直线和双曲线的图象上,
,.
(2)如图1中,设直线与反比例函数的另一个交点为.
由对称性可知:,
当点与重合时,,此时.
当点在的延长线上时,时,,此时,
综上所述,满足条件的点的坐标为或.
(3)如图2中,将绕点顺时针旋转得到,则,
取的中点,作直线在第二象限交反比例函数于.此时,
,,
直线的解析式为,
由,解得或,
点在第二象限,
,.
28.如图,等边,点为射线上一点,延长至点,使得,联结并延长交射线于点.
(1)当点在边上时,如图1,若,则 ;
(2)当点在边上时;如图2,若,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明;
(3)当点在的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明.
【分析】(1)由等边三角形的性质可得,,,可求,即可求解;
(2)如图2,过点作交的延长线于,可证是等边三角形,可得,通过证明,可得,由外角性质可求解;
(3)如图3,过点作交的延长线于,可证是等边三角形,可得,通过证明,可得,由外角性质可求解;
【解答】解:(1)是等边三角形,,
,,,
,,
,
,
,
故答案为:;
(2)如图2,过点作交的延长线于,
,
,,
是等边三角形,
,
,
,
,
,
,,,
,
,
;
(3)如图3,过点作交的延长线于,
,
,,,
是等边三角形,
,
,
,
,
,
,,,
,
,,
,
,
.
期中数学试卷
一、选择题(本大题共6题)
1.在下列方程中,一元二次方程的个数是
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
2.方程的根为
A. B. C., D.,
3.已知函数中随的增大而增大,那么它和函数在同一直角坐标系内的大致图象可能是
A. B.
C. D.
4.到一个三角形三个顶点的距离都相等的点是这个三角形
A.三条中线的交点 B.三条高的交点
C.三边中垂线的交点 D.三条角平分线的交点
5.下列说法错误的是
A.到点距离等于的点的轨迹是以点为圆心,半径长为的圆
B.等腰的底边固定,顶点的轨迹是线段的垂直平分线
C.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
D.到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线
6.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
二、填空题(本大题共12题,每题2分,满分24分)
7.函数的定义域是 .
8.方程的解为 .
9.方程的根是 .
10.在实数范围内因式分解: .
11.已知正比例函数的图象经过第一、三象限,则的取值范围是 .
12.已知点,和,都在反比例函数的图象上,若,则、的大小关系是 .
13.命题“平行于同一直线的两直线平行”的逆命题是: .
14.某企业生产某种产品,今年产量为200件,计划通过技术革新,三年(包括今年)的产量达到1400件,若明后两年的产量平均增长率相同为,可以得到方程: .
15.在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于,,作直线,交于点,连接.如果,,那么 .
16.如图,已知在中,是边上的高,平分,交于点,,,则的面积等于 .
17.如图,中,平分,的中垂线交于点,交于点,连接,.若为等腰三角形,则的度数为 .
18.如图,在中,,的平分线与的外角平分线交于点,则的度数为 .(用含的式子表示)
三、简答题(本大题共4题)
19.解方程:
20.用配方法解方程:
21.解方程:
22.已知:、点及线段(如图).求作:点,使得点到和的距离相等,且.(要求尺规作图,保留作图痕迹,不必写作法和证明)
四、解答题(本大题共4题)
23.已知关于的一元二次方程有两个不相等的实数根,求的取值范围.
24.小芸家与学校之间是一条笔直的公路,小芸从家步行前往学校的途中发现忘记带阅读分享要用的盘,便停下给妈妈打电话,妈妈接到电话后,带上盘马上赶往学校,同时小芸沿原路返回.两人相遇后,小芸立即赶往学校,妈妈沿原路返回家,并且小芸到达学校比妈妈到家多用了5分钟.若小芸步行的速度始终是每分钟100米,小芸和妈妈之间的距离与小芸打完电话后步行的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)妈妈从家出发 分钟后与小芸相遇;
(2)相遇后妈妈回家的平均速度是每分钟 米;
(3)小芸家离学校的距离为 米.
25.如图,点,,,在同一条直线上,,在以下三个论断“,,”中选择两个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点,,,在同一条直线上,, .
求证: .
证明:
26.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加,且所种桃树要少于原有桃树,那么应多种多少棵桃树?
五、综合题(本大题共2题)
27.在平面直角坐标系中(如图),点为直线和双曲线的一个交点.
(1)求、的值;
(2)若点,在直线上有一点,使得,请求出点的坐标;
(3)在双曲线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
28.如图,等边,点为射线上一点,延长至点,使得,联结并延长交射线于点.
(1)当点在边上时,如图1,若,则 ;
(2)当点在边上时;如图2,若,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明;
(3)当点在的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明.
2019-2020学年上海市徐汇区西南模范中学八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共6题,每题2分,满分12分)
1.在下列方程中,一元二次方程的个数是
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
【分析】本题根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.
【解答】解:①,是一元二次方程,故本小题正确;
②,时是一元二次方程,故本小题错误;
③,整理后不是一元二次方程,故本小题错误;
④,是分式方程,不是一元二次方程,故本小题错误.
故选:.
2.方程的根为
A. B. C., D.,
【分析】两边直接开平方法求解可得.
【解答】解:,
或,
解得:或,
故选:.
3.已知函数中随的增大而增大,那么它和函数在同一直角坐标系内的大致图象可能是
A. B.
C. D.
【分析】先根据正比例函数的性质判断出的符号,再根据反比例函数的性质利用排除法求解即可.
【解答】解:函数中随的增大而增大,
,
函数的图象经过一、三象限,故可排除、;
,
,
函数的图象在二、四象限,故错误,正确.
故选:.
4.到一个三角形三个顶点的距离都相等的点是这个三角形
A.三条中线的交点 B.三条高的交点
C.三边中垂线的交点 D.三条角平分线的交点
【分析】根据线段的操作票个方向的性质即可判断.
【解答】解:三角形的三边的中垂线到三个顶点距离相等,
故选:.
5.下列说法错误的是
A.到点距离等于的点的轨迹是以点为圆心,半径长为的圆
B.等腰的底边固定,顶点的轨迹是线段的垂直平分线
C.在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线
D.到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线
【分析】利用圆的定义,线段垂直平分线的性质,等腰三角形的性质,角平分线的性质依次判断即可求解.
【解答】解:、到点距离等于的点的轨迹是以点为圆心,半径为的圆,故选项不符合题意;
、等腰的底边固定,顶点的轨迹是线段的垂直平分线(线段中点除外),故选项符合题意;
、在一个角的内部(包括顶点)到角的两边距离相等的点的轨迹是这个角的平分线,故选项不符合题意;
、到直线的距离等于的点的轨迹是两条平行于且与的距离等于的直线,故选项不符合题意;
故选:.
6.如图,中,的垂直平分线交边于点,的垂直平分线交边于点,若,则的度数为
A. B. C. D.
【分析】根据三角形内角和定理可求,根据垂直平分线性质,,,则,,从而可得,即可得到,即可得解.
【解答】解:,
,
的垂直平分线交边于点,的垂直平分线交边于点,
,,
,,
,
,
.
故选:.
二、填空题(本大题共12题,每题2分,满分24分)
7.函数的定义域是 .
【分析】当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零,依此即可求解.
【解答】解:依题意有,
解得.
故答案为:.
8.方程的解为 .
【分析】根据配方法可以解答本题.
【解答】解:,
,
所以,,
故答案为.
9.方程的根是 或 .
【分析】利用因式分解法求解可得.
【解答】解:,
,
则,
或,
解得或,
故答案为:或.
10.在实数范围内因式分解: .
【分析】利用求根公式求得关于的一元二次方程的两根,然后利用公式法进行因式分解.
【解答】解:解关于的一元二次方程得到:,.
所以.
故答案是:.
11.已知正比例函数的图象经过第一、三象限,则的取值范围是 .
【分析】先根据正比例函数的图象经过第一、三象限列出关于的不等式,求出的取值范围即可.
【解答】解:正比例函数的图象经过第一、三象限,
,
.
故答案为:.
12.已知点,和,都在反比例函数的图象上,若,则、的大小关系是 .
【分析】反比例函数的图象位于一、三象限,在每个象限内,随的增大而减小,又,可得到点,和,在第三象限图象上的两点,可得
【解答】解:,
在每个象限内,随的增大而减小,
又,
可得,
故答案为:
13.命题“平行于同一直线的两直线平行”的逆命题是: “如果两直线平行于同一直线,那么这两条直线平行” .
【分析】把一个命题的条件和结论互换就得到它的逆命题.
【解答】解:命题“平行于同一直线的两直线平行”的逆命题是:“如果两直线平行于同一直线,那么这两条直线平行”,
故答案为:“如果两直线平行于同一直线,那么这两条直线平行”.
14.某企业生产某种产品,今年产量为200件,计划通过技术革新,三年(包括今年)的产量达到1400件,若明后两年的产量平均增长率相同为,可以得到方程: .
【分析】设明后两年的产量平均增长率为,根据三年(包括今年)的产量达到1400件,即可得出关于的一元二次方程,此题得解.
【解答】解:设明后两年的产量平均增长率为,
依题意,得:.
故答案为:.
15.在中,分别以点和点为圆心,大于的长为半径画弧,两弧相交于,,作直线,交于点,连接.如果,,那么 3 .
【分析】直接利用基本作图方法得出垂直平分,进而得出答案.
【解答】解:由作图步骤可得:垂直平分,则,
,,
.
故答案为:3.
16.如图,已知在中,是边上的高,平分,交于点,,,则的面积等于 5 .
【分析】过作于点,由角平分线的性质可求得,则可求得的面积.
【解答】解:
过作于点,
是边上的高,平分,
,
,
故答案为:5.
17.如图,中,平分,的中垂线交于点,交于点,连接,.若为等腰三角形,则的度数为 或或 .
【分析】根据角平分线的定义求出的度数,根据线段垂直平分线的性质得到,根据等腰三角形的性质得到答案.
【解答】解:平分,
,
是的中垂线,
,
,
,
为等腰三角形,
当,
,
,
,
当,
,
,
,
当,
,
,
综上所述,的度数为或或,
故答案为:或或.
18.如图,在中,,的平分线与的外角平分线交于点,则的度数为 .(用含的式子表示)
【分析】首先证明也是的外角的平分线,根据平角的定义和角平分线的定义求得,的度数,最后根据三角形的内角和定理即可求得.
【解答】解:在的平分线上,
点到的距离等于到的距离,
在的外角的平分线上,
点到的距离等于到的距离,
点到的距离等于到的距离,
是的外角的平分线,
,
,
故答案为.
三、简答题(本大题共4题,每题5分,满分20分)
19.解方程:
【分析】先把方程化为一般式,再计算判别式的值,然后利用求根公式求解.
【解答】解:,
,
,,
△,
,
所以,.
20.用配方法解方程:
【分析】方程二次项系数化为1,常数项移到右边,利用完全平方公式配方后,开方即可求出解.
【解答】解:方程整理得:,
配方得:,即,
或,
,.
21.解方程:
【分析】先将方程化为一般形式,确定,,的值,然后代入求根公式进行计算即可.
【解答】解:,
整理得:,
,,,△,
.
即,.
22.已知:、点及线段(如图).求作:点,使得点到和的距离相等,且.(要求尺规作图,保留作图痕迹,不必写作法和证明)
【分析】根据角平分线上的点到角的两边的距离相等可得点在的平分线上,然后再以点为圆心,以的长度为半径画弧,与的平分线相交于一点,交点就是所求的点.
【解答】解:
所以两个位置的点就是所要求作的点.
每作对一个点得2分,共4分;结论2分.
四、解答题(本大题共4题,每题6分,满分24分)
23.已知关于的一元二次方程有两个不相等的实数根,求的取值范围.
【分析】由方程有两个不相等的实数根,根据根的判别式可得到关于的不等式,可求得的取值范围.
【解答】解:方程有两个不相等的实数根,
△且且即且且,
解得且.
故的取值范围是且.
24.小芸家与学校之间是一条笔直的公路,小芸从家步行前往学校的途中发现忘记带阅读分享要用的盘,便停下给妈妈打电话,妈妈接到电话后,带上盘马上赶往学校,同时小芸沿原路返回.两人相遇后,小芸立即赶往学校,妈妈沿原路返回家,并且小芸到达学校比妈妈到家多用了5分钟.若小芸步行的速度始终是每分钟100米,小芸和妈妈之间的距离与小芸打完电话后步行的时间之间的函数关系如图所示,根据图象回答下列问题:
(1)妈妈从家出发 8 分钟后与小芸相遇;
(2)相遇后妈妈回家的平均速度是每分钟 米;
(3)小芸家离学校的距离为 米.
【分析】(1)根据函数图象中的数据可知妈妈从家出发几分钟后与小芸相遇;
(2)根据函数图象中的数据可以求得相遇后妈妈回家的平均速度;
(3)根据函数图象中的数据可以求得小芸家离学校的距离.
【解答】解:(1)由图象可得,
妈妈从家出发8分钟后与小芸相遇,
故答案为:8;
(2)相遇后妈妈回家的平均速度是每分钟:(米,
故答案为:60;
(3)小芸家离学校的距离为:(米,
故答案为:2100.
25.如图,点,,,在同一条直线上,,在以下三个论断“,,”中选择两个作为已知条件,另一个作为结论,构成真命题(补充已知和求证),并进行证明.
已知:如图,点,,,在同一条直线上,, , .
求证: .
证明:
【分析】根据题意写出已知、求证,根据线段垂直平分线的判定定理证明.
【解答】已知:如图,点,,,在同一条直线上,,,,
求证:,
证明:,
点在线段的垂直平分线上,
点在线段的垂直平分线上,
,
点在线段的垂直平分线上,
,
故答案为:,;.
26.某果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵桃树的产量就会减少2个,如果要使产量增加,且所种桃树要少于原有桃树,那么应多种多少棵桃树?
【分析】每多种一棵桃树,每棵桃树的产量就会减少2个,所以多种棵树每棵桃树的产量就会减少个(即是平均产个),桃树的总共有棵,所以总产量是个.要使产量增加,达到个.
【解答】解:设应多种棵桃树,则由题意可得:
整理,得:,
即,
解得:,
因为所种桃树要少于原有桃树,
所以不符合题意,应舍去,取,
答:应多种20棵桃树.
五、综合题(本大题共2题,每题10分,满分20分)
27.在平面直角坐标系中(如图),点为直线和双曲线的一个交点.
(1)求、的值;
(2)若点,在直线上有一点,使得,请求出点的坐标;
(3)在双曲线上是否存在点,使得,若存在,请求出点的坐标;若不存在,请说明理由.
【分析】(1)利用待定系数法即可解决问题.
(2)如图1中,设直线与反比例函数的另一个交点为.由对称性可知:,推出当点与重合时,,此时.当点在的延长线上时,时,,再利用中点坐标公式求解即可.
(3)如图2中,将绕点顺时针旋转得到,则,取的中点,作直线在第二象限交反比例函数于.此时,求出直线的解析式,再构建方程组确定点的坐标.
【解答】解:(1)点在直线和双曲线的图象上,
,.
(2)如图1中,设直线与反比例函数的另一个交点为.
由对称性可知:,
当点与重合时,,此时.
当点在的延长线上时,时,,此时,
综上所述,满足条件的点的坐标为或.
(3)如图2中,将绕点顺时针旋转得到,则,
取的中点,作直线在第二象限交反比例函数于.此时,
,,
直线的解析式为,
由,解得或,
点在第二象限,
,.
28.如图,等边,点为射线上一点,延长至点,使得,联结并延长交射线于点.
(1)当点在边上时,如图1,若,则 ;
(2)当点在边上时;如图2,若,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明;
(3)当点在的延长线上时,则(1)的结论还成立吗?若成立,请证明;若不成立,写出与的数量关系并证明.
【分析】(1)由等边三角形的性质可得,,,可求,即可求解;
(2)如图2,过点作交的延长线于,可证是等边三角形,可得,通过证明,可得,由外角性质可求解;
(3)如图3,过点作交的延长线于,可证是等边三角形,可得,通过证明,可得,由外角性质可求解;
【解答】解:(1)是等边三角形,,
,,,
,,
,
,
,
故答案为:;
(2)如图2,过点作交的延长线于,
,
,,
是等边三角形,
,
,
,
,
,
,,,
,
,
;
(3)如图3,过点作交的延长线于,
,
,,,
是等边三角形,
,
,
,
,
,
,,,
,
,,
,
,
.
同课章节目录
