人教版八年级数学下册18.1.1平行四边形的性质课件(共18张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.1平行四边形的性质课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 751.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
*
护理实习报告总结范文参考
实习报告怎么写如何才能写得好实习报告为您提供优秀的实习报告范文、实习报告模板、实习报告格式等,一定能帮你写出一篇优秀的实习报告。网站内容时时更新,欢迎您收藏本网站,。
十个月的时间好快,真的好快,一晃就过去了,我们告别了我们的护士实习生活,也永远告别了我们的学生时代,在这一年时间了,我们收获了好多,收获了知识,技术,友情,经验……
那一天我们穿上洁白的护士服进入医院的时候,心情是多么的激动,那一刻告诉我们——保护生命、减轻痛苦、增进健康是我们护士的职责,作为一名实习护士,我们应该在医院认真努力学习,使自己获得扎实的专业理论知识和娴熟的护理操作技能,这样才能为我们以后成为一名合格的护士垫下基础!
实习伊始,我们几个小护士总是跟在带教老师的屁股后面,不放过老师的每一个操作细节,有的还做了小笔记,遇到不懂的我们都及时地向老师询问,老师总能给我们细细解答,虽然有的老师态度不是很好,但是我们都能理解的,护士工作确实非常的繁杂,老师要做好自己本分的工作还要负起带教的责任。就这样刚开始我们做了几个礼拜的见习护
士,渐渐的我们开始尝试操作,而老师只放手不放眼,让我们安心地去操
§19.1.1
平行四边形的性质
*
下面的图片中,有你熟悉的哪些图形?
活动 1
*
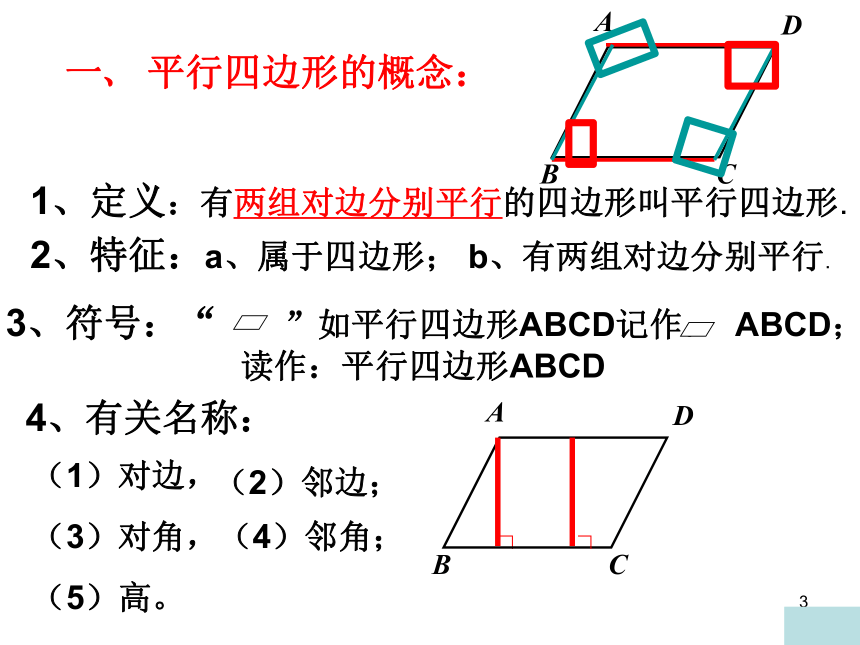
一、 平行四边形的概念:
1、定义:有两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
∟
∟
*
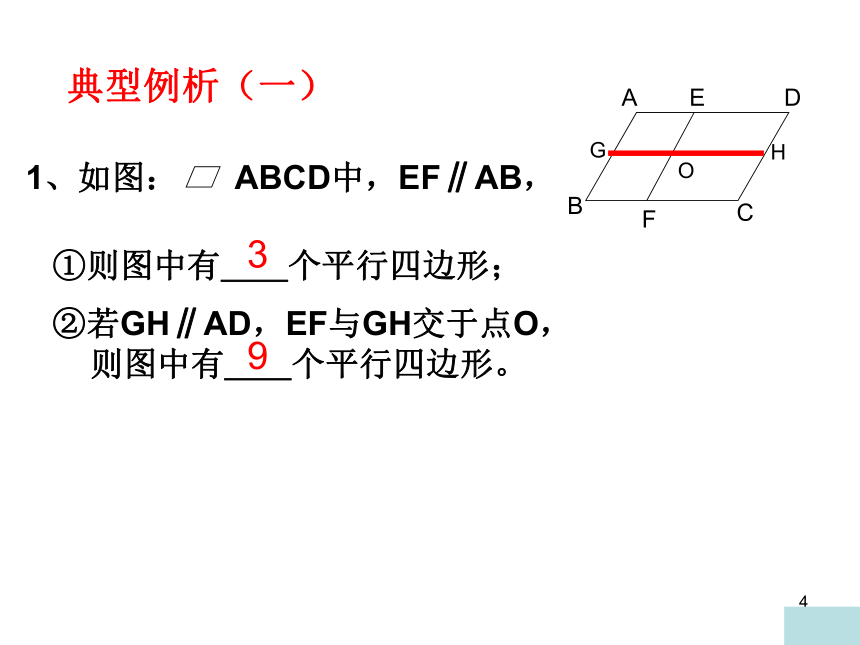
典型例析(一)
①则图中有__个平行四边形;
3
9
*
二、平行四边形性质探究
1、画一个 ABCD
2、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA
3、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D
*
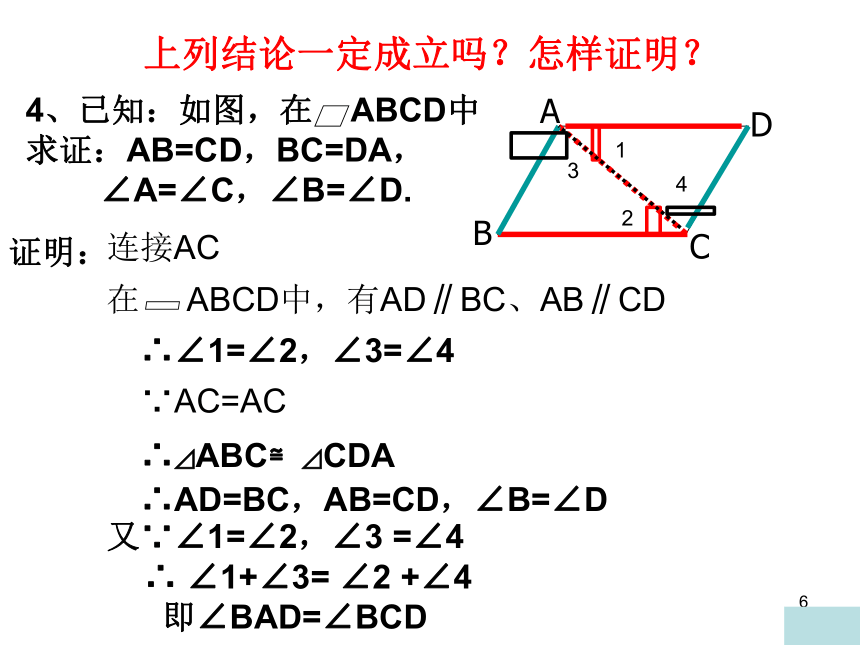
上列结论一定成立吗?怎样证明?
4、已知:如图,在 ABCD中
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
证明:
连接AC
∴∠1=∠2,∠3=∠4
∵AC=AC
∴⊿ABC≌⊿CDA
∴AD=BC,AB=CD,∠B=∠D
又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD
*
平行四边形性质
1、边:
2、角:
对角相等,邻角互补
3、周长:
两邻边之和×2
对边平行且相等
4、面积:
边长×边长上的高
*
典型例析(二)
例:如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
A:基础知识:
B:变式训练:
1、若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
2、若∠A:∠B= 5:4,则∠C=______ 、∠D=______
50°
130°
50°
100°
80°
100°
80°
*
C:拓展延伸:
例:如图,在
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
2、连接AC,若∠D=80°, ∠DAC=40°则, ∠B=___
∠BAC=____,
B
80°
60°
120°
60°
*
典型例析(三)
例:如图在
A基础知识:
1、若AB=1㎝,BC=2 ㎝
B变式训练:
1、若AB:BC=3:4,周长为14㎝,则CD=——,DA=——
2、若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____
C拓展延伸:
若AB=x-4,BC=x+3,CD=6㎝,则AD=______
6cm
5cm
3cm
4cm
8cm
28cm
13cm
*
典型例析(四)综合发散
AB=5,BC=9,BE平分∠ABC,
4
1、如图,
则DE= _________
1
2
3
*
A
B
C
D
12
5
4
3
*
:有两组对边分别相等的平行四边形。
面积
周长
角
边
(3)性质的应用
本节课主要学习了哪些知识?
(2)平行四边形的性质
(1)平行四边形定义
*
作业设计(必做题)
(1) ABCD中∠A:∠B=1:2 则∠C = 度 ,
∠D = 度
(2) ABCD中,外角∠CBE=70°,则∠D= 度
60
120
110
2(a+b)
*
(1)如图 ABCD中AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____
作业设计(选做题)
(2)如图
AB=AC=10,则
周长为_____
B
A
C
D
F
E
4
4
1
20
*
(1)、如图
B
E
D
C
A
S1
S
S2
*
PD∥ AB,PE ∥AC,PF ∥BC, 则
(2)等边
ABC的边长为10,P为 ABC内一点,
PD+PE+PF的值为______
D
F
P
C
E
B
A
*
E
(3)、如图, ∠ABC=3∠C,点F在
CB延长线上,FE⊥CD,AD=CE=1,则
BF=______
ABCD中
C
B
F
D
A
*
护理实习报告总结范文参考
实习报告怎么写如何才能写得好实习报告为您提供优秀的实习报告范文、实习报告模板、实习报告格式等,一定能帮你写出一篇优秀的实习报告。网站内容时时更新,欢迎您收藏本网站,。
十个月的时间好快,真的好快,一晃就过去了,我们告别了我们的护士实习生活,也永远告别了我们的学生时代,在这一年时间了,我们收获了好多,收获了知识,技术,友情,经验……
那一天我们穿上洁白的护士服进入医院的时候,心情是多么的激动,那一刻告诉我们——保护生命、减轻痛苦、增进健康是我们护士的职责,作为一名实习护士,我们应该在医院认真努力学习,使自己获得扎实的专业理论知识和娴熟的护理操作技能,这样才能为我们以后成为一名合格的护士垫下基础!
实习伊始,我们几个小护士总是跟在带教老师的屁股后面,不放过老师的每一个操作细节,有的还做了小笔记,遇到不懂的我们都及时地向老师询问,老师总能给我们细细解答,虽然有的老师态度不是很好,但是我们都能理解的,护士工作确实非常的繁杂,老师要做好自己本分的工作还要负起带教的责任。就这样刚开始我们做了几个礼拜的见习护
士,渐渐的我们开始尝试操作,而老师只放手不放眼,让我们安心地去操
§19.1.1
平行四边形的性质
*
下面的图片中,有你熟悉的哪些图形?
活动 1
*
一、 平行四边形的概念:
1、定义:有两组对边分别平行的四边形叫平行四边形.
2、特征:a、属于四边形; b、有两组对边分别平行.
4、有关名称:
(3)对角,(4)邻角;
(5)高。
∟
∟
*
典型例析(一)
①则图中有__个平行四边形;
3
9
*
二、平行四边形性质探究
1、画一个 ABCD
2、度量对边AB与CD的长,BC与DA的长,可得什么结论?
AB=CD BC=DA
3、度量对角∠A与∠C, ∠B与∠D的大小,可得什么结论?
∠A=∠C ∠B=∠D
*
上列结论一定成立吗?怎样证明?
4、已知:如图,在 ABCD中
求证:AB=CD,BC=DA,
∠A=∠C,∠B=∠D.
证明:
连接AC
∴∠1=∠2,∠3=∠4
∵AC=AC
∴⊿ABC≌⊿CDA
∴AD=BC,AB=CD,∠B=∠D
又∵∠1=∠2,∠3 =∠4
∴ ∠1+∠3= ∠2 +∠4
即∠BAD=∠BCD
*
平行四边形性质
1、边:
2、角:
对角相等,邻角互补
3、周长:
两邻边之和×2
对边平行且相等
4、面积:
边长×边长上的高
*
典型例析(二)
例:如图,在
若∠A=130°,则∠B=______ 、∠C=______ 、∠D=______
A:基础知识:
B:变式训练:
1、若∠A+ ∠C= 200°,则∠A=______ 、∠B=______
2、若∠A:∠B= 5:4,则∠C=______ 、∠D=______
50°
130°
50°
100°
80°
100°
80°
*
C:拓展延伸:
例:如图,在
1、∠A:∠B: ∠C :∠D的度数可能是( )
A、1:2:3:4 B、3:2:3:2 C、2:3:3:2 D、2:2:3:3
2、连接AC,若∠D=80°, ∠DAC=40°则, ∠B=___
∠BAC=____,
B
80°
60°
120°
60°
*
典型例析(三)
例:如图在
A基础知识:
1、若AB=1㎝,BC=2 ㎝
B变式训练:
1、若AB:BC=3:4,周长为14㎝,则CD=——,DA=——
2、若AB:BC=3:4,AB=6 ㎝,则BC=____,周长=_____
C拓展延伸:
若AB=x-4,BC=x+3,CD=6㎝,则AD=______
6cm
5cm
3cm
4cm
8cm
28cm
13cm
*
典型例析(四)综合发散
AB=5,BC=9,BE平分∠ABC,
4
1、如图,
则DE= _________
1
2
3
*
A
B
C
D
12
5
4
3
*
:有两组对边分别相等的平行四边形。
面积
周长
角
边
(3)性质的应用
本节课主要学习了哪些知识?
(2)平行四边形的性质
(1)平行四边形定义
*
作业设计(必做题)
(1) ABCD中∠A:∠B=1:2 则∠C = 度 ,
∠D = 度
(2) ABCD中,外角∠CBE=70°,则∠D= 度
60
120
110
2(a+b)
*
(1)如图 ABCD中AB=5,BC=9,BE,CF分别平分∠ABC, ∠BCD,则DE=_____,AF=_____,EF=_____
作业设计(选做题)
(2)如图
AB=AC=10,则
周长为_____
B
A
C
D
F
E
4
4
1
20
*
(1)、如图
B
E
D
C
A
S1
S
S2
*
PD∥ AB,PE ∥AC,PF ∥BC, 则
(2)等边
ABC的边长为10,P为 ABC内一点,
PD+PE+PF的值为______
D
F
P
C
E
B
A
*
E
(3)、如图, ∠ABC=3∠C,点F在
CB延长线上,FE⊥CD,AD=CE=1,则
BF=______
ABCD中
C
B
F
D
A
