(新教材)2019-2020学年新素养同步人教A版高中数学必修第二册学案:9.2.1 总体取值规律的估计9.2.2 总体百分位数的估计Word版含答案
文档属性
| 名称 | (新教材)2019-2020学年新素养同步人教A版高中数学必修第二册学案:9.2.1 总体取值规律的估计9.2.2 总体百分位数的估计Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览




文档简介
9.2 用样本估计总体
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
考点
学习目标
核心素养
频率分布表、频率分布直方图
会画一组数据的频率分布表、频率分布直方图
直观想象、数据分析
用样本估计总体
会用频率分布表、频率分布直方图、条形图、扇形图、折线图等对总体进行估计
直观想象、数据分析
总体百分位数的估计
掌握求n个数据的第p百分位数的方法
数学抽象、数学运算
问题导学
预习教材P192-P202的内容,思考以下问题:
1.绘制频率分布表和频率分布直方图有哪些步骤?
2.频率分布直方图有哪些特征?
3.如何求n个数据的第p百分位数?
1.频率分布表、频率分布直方图的制作步骤及意义
2.百分位数
(1)定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)计算步骤:计算一组n个数据的第p百分位数的步骤:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
判断(正确的打“√”,错误的打“×”)
(1)直方图的高表示取某数的频率.( )
(2)直方图的高表示该组上的个体在样本中出现的频率.( )
(3)直方图的高表示取某组上的个体在样本中出现的频数与组距的比值.( )
(4)直方图的高表示取该组上的个体在样本中出现的频率与组距的比值.( )
解析:要注意频率分布直方图的特点.在直方图中,纵轴(矩形的高)表示频率与组距的比值,其相应组距上的频率等于该组距上的矩形的面积.
答案:(1)× (2)× (3)× (4)√
一个容量为80的样本中数据的最大值是140,最小值是51,组距是10,则应将样本数据分为( )
A.10组
B.9组
C.8组
D.7组
解析:选B.极差为140-51=89,而组距为10,故应将样本数据分为9组.
将容量为100的样本数据按由小到大排列分成8个小组,如表所示,但第3组被墨汁污染,则第三组的频率为( )
组号
1
2
3
4
5
6
7
8
频数
10
13
14
15
13
12
9
A.0.14
B.0.12
C.0.03
D.0.10
解析:选A.第三组的频数为100-(10+13+14+15+13+12+9)=14.故第三组的频率为=0.14.
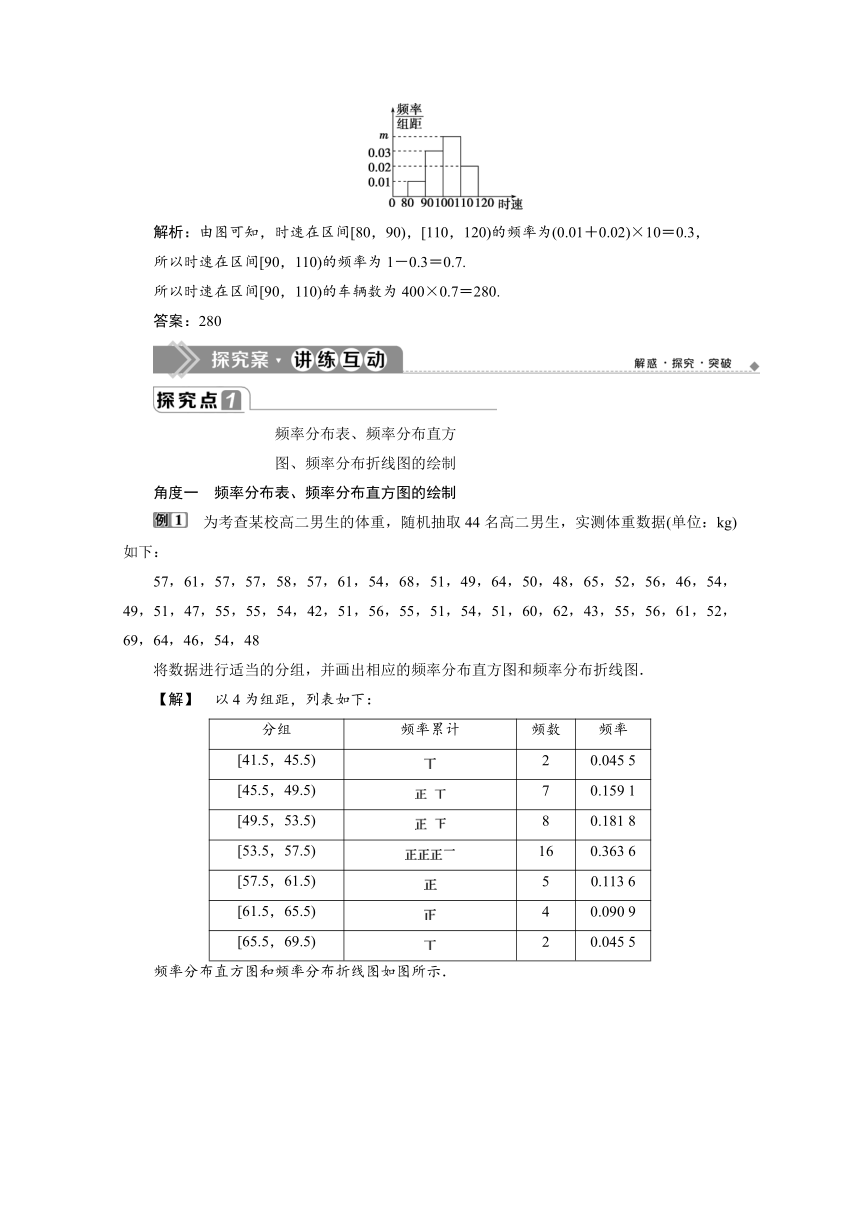
(2019·四川省绵阳市教学质量测试)某高速公路移动雷达测速检测车在某时段对某段路过往的400辆汽车的车速进行检测,根据检测的结果绘制出如图所示的频率分布直方图,根据直方图的数据估计400辆汽车中时速在区间[90,110)的约有____________辆.
解析:由图可知,时速在区间[80,90),[110,120)的频率为(0.01+0.02)×10=0.3,
所以时速在区间[90,110)的频率为1-0.3=0.7.
所以时速在区间[90,110)的车辆数为400×0.7=280.
答案:280
频率分布表、频率分布直方
图、频率分布折线图的绘制
角度一 频率分布表、频率分布直方图的绘制
为考查某校高二男生的体重,随机抽取44名高二男生,实测体重数据(单位:kg)如下:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48
将数据进行适当的分组,并画出相应的频率分布直方图和频率分布折线图.
【解】 以4为组距,列表如下:
分组
频率累计
频数
频率
[41.5,45.5)
2
0.045
5
[45.5,49.5)
7
0.159
1
[49.5,53.5)
8
0.181
8
[53.5,57.5)
16
0.363
6
[57.5,61.5)
5
0.113
6
[61.5,65.5)
4
0.090
9
[65.5,69.5)
2
0.045
5
频率分布直方图和频率分布折线图如图所示.
(1)在列频率分布表时,极差、组距、组数有如下关系:
①若为整数,则=组数;
②若不为整数,则的整数部分+1=组数.
(2)组距和组数的确定没有固定的标准,将数据分组时,组数力求合适,纵使数据的分布规律能较清楚地呈现出来,组数太多或太少,都会影响我们了解数据的分布情况,若样本容量不超过100,按照数据的多少常分为5~12组,一般样本量越大,所分组数越多.
角度二 频率分布直方图的应用
为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率是多少?
(3)样本中不达标的学生人数是多少?
(4)第三组的频数是多少?
【解】 (1)频率分布直方图以面积的形式反映数据落在各小组内的频率大小,因此第二小组的频率为=0.08.
又因为第二小组的频率=,
所以样本容量===150.
(2)由直方图可估计该校高一年级学生的达标率为×100%=88%.
(3)由(1)(2)知达标率为88%,样本量为150,不达标的学生频率为1-0.88=0.12.
所以样本中不达标的学生人数为150×0.12=18(人).
(4)第三小组的频率为=0.34.
又因为样本量为150,
所以第三组的频数为150×0.34=51.
频率分布直方图的应用中的计算问题
(1)小长方形的面积=组距×=频率;
(2)各小长方形的面积之和等于1;
(3)=频率,此关系式的变形为=样本量,样本量×频率=频数.
某厂对一批产品进行抽样检测,如图是抽检产品净重(单位:克)的频率分布直方图,样本数据分组为[76,78),[78,80),…,[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是( )
A.12
B.18
C.25
D.90
解析:选D.净重大于或等于78克且小于84克的频率为(0.100+0.150+0.125)×2=0.75,所以在该范围内的产品个数为120×0.75=90.
条形统计图
为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如图所示.
请根据统计图提供的信息回答以下问题:
(1)求抽取的学生数;
(2)若该校有3
000名学生,估计喜欢收听易中天《品三国》的学生人数;
(3)估计该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的百分比.
【解】 (1)从统计图上可以看出,
喜欢收听于丹析《庄子》的男生有20人,女生有10人;
喜欢收听《故宫博物院》的男生有30人,女生有15人;
喜欢收听于丹析《论语》的男生有30人,女生有38人;
喜欢收听易中天《品三国》的男生有64人,女生有42人;
喜欢收听刘心武评《红楼梦》的男生有6人,女生有45人.
所以抽取的学生数为20+10+30+15+30+38+64+42+6+45=300(人).
(2)喜欢收听易中天《品三国》的男生有64人,女生有42人,共有106人,占所抽取总人数的比例为,
由于该校有3
000名学生,因此可以估计喜欢收听易中天《品三国》的学生有×3
000=1
060(人).
(3)该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的比例为×100%=15%.
(1)绘制条形统计图时,第一步确定坐标系中横轴和纵轴上坐标的意义,第二步确定横轴上各部分的间距及位置,第三步根据统计结果绘制条形图.
实际问题中,我们需根据需要进行分组,横轴上的分组越细,对数据的刻画(描述)就越精确.
(2)在条形统计图中,各个矩形图的宽度没有严格要求,但高度必须以数据为准,它直观反映了各部分在总体中所占比重的大小.
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层随机抽样调查,测得身高情况的统计图如图所示.
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185
cm之间的学生占总人数的百分比是多少.
解:(1)样本中男生人数为40,由分层随机抽样比例为10%估计全校男生人数为400.
(2)由统计图知,样本身高在170~185
cm之间的学生有14+13+4+3+1=35(人),样本容量为70,所以在样本中学生身高在170~185
cm之间所占比例为=50%,故可估计该校学生身高在170~185
cm之间的学生占总人数的50%.
折线统计图
小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每隔几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么出院?
【解】 (1)根据横轴表示的意义,可知护士每隔6小时给小明测量一次体温.
(2)从折线统计图中的最高点和最低点对应的纵轴意义,可知最高体温是39.5摄氏度,最低体温是36.8摄氏度.
(3)从图中可知小明的体温已经下降,并趋于稳定,因此病情在好转.
(4)9月8日18时小明的体温是37摄氏度.其后的体温未超过37.2摄氏度,自9月8日18时起计算,连续36小时后对应的时间为9月10日凌晨6时.因此小明最快可以在9月10凌晨6时出院.
(1)绘制折线统计图时,第一步,确定直角坐标系中横、纵坐标表示的意义;第二步,确定一个单位长度表示一定的数量,根据数量的多少描出各点;第三步,用直线段顺次连接即可.
(2)在折线统计图中,从折线的上升、下降可分析统计数量的增减变化情况,从陡峭程度上,可分析数据间相对增长、下降的幅度.
据报道,去年某咨询公司对1
500个家庭进行了关于奶粉市场的调查,下图是关于每月购买奶粉袋数的有关数据,则每月购买1袋奶粉的比率同每月购买2袋奶粉的比率合计为( )
A.79.9%
B.70.9%
C.38.8%
D.32.1%
解析:选B.根据折线图,每月购买1袋奶粉和每月购买2袋奶粉的比率分别为38.8%和32.1%,故所求为38.8%+32.1%=70.9%.
扇形统计图
下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图:
(1)从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
【解】 (1)不能.因为两所学校收到艺术作品的总数不知道.
(2)设A学校收到艺术作品的总数为x件,B学校收到艺术作品的总数为y件,则解得即A学校收到艺术作品的总数为500件,B学校收到艺术作品的总数为600件.
(1)绘制扇形统计图时,第一步计算各部分所占百分比以及对应圆心角的度数;第二步在圆中按照上述圆心角画出各个扇形并恰当标注.
(2)扇形统计图表示总体的各部分之间的百分比关系,但不同总量下的扇形统计图,其不同的百分比不可以作为比较的依据.
如图是2019年各级学校每10万人口中平均在校生的人数扇形统计图,则下列结论正确的是( )
A.2019年有6%的高中生升入高等学校
B.2019年全国高等学校在校生6
000人
C.2019年各级学校10万人口平均在校生数在高等学校学生中占6%
D.2019年高等学校的学生比高中阶段的学生多
解析:选C.由扇形统计图可以看出,2019年各级学校每10万人口中平均在校生的人数所占的百分比分别为幼儿园占8%,高等学校占6%,高中阶段占12%,初中阶段占26%,小学占48%,A项中应是高等学校在校学生.B项中6
000人应是平均数,D项显然错误.
百分位数的计算
现有甲、乙两组数据如下表所示.
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
甲组
1
2
2
2
2
3
3
3
5
5
6
6
8
8
9
10
10
12
13
13
乙组
0
0
0
0
1
1
2
3
4
5
6
6
7
7
10
14
14
14
14
15
试求甲、乙两组数的25%分位数与75%分位数.
【解】 因为数据个数为20,而且20×25%=5,20×75%=15.
因此,甲组数的25%分位数为==2.5;
甲组数的75%分位数为==9.5.
乙组数的25%分位数为==1,乙组的75%分位数为==12.
求百分位数时,一定要将数据按照从小到大的顺序排列.
求1,2,3,4,5,6,7,8,9,10的25%分位数,75%分位数,90%分位数.
解:因为数据个数为10,而且10×25%=2.5,10×75%=7.5,10×90%=9.
所以该组数据的25%分位数为x3=3,75%分位数为x8=8,90%分位数为==9.5.
1.下列四个图中,用来表示不同品种的奶牛的平均产奶量最为合适的是( )
解析:选D.用统计图表示不同品种的奶牛的平均产奶量,即从图中可以比较各种数量的多少,因此“最为合适”的统计图是条形统计图.注意B选项中的图不能称为统计图.
2.观察新生儿的体重,其频率分布直方图如图所示,则新生儿体重在[2
700,3
000)g的频率为( )
A.0.1
B.0.2
C.0.3
D.0.4
解析:选C.由题图可得,新生儿体重在[2
700,3
000)g的频率为0.001×300=0.3,故选C.
3.观察下图所示的统计图,下列结论正确的是( )
A.甲校女生比乙校女生多
B.乙校男生比甲校男生少
C.乙校女生比甲校男生少
D.甲、乙两校女生人数无法比较
解析:选D.图中数据只是百分比,甲、乙两个学校的学生总数不知道,因此男生与女生的具体人数也无法得知.
4.(2019·广西钦州市期末考试)为了了解某城市居民用水量情况,我们抽取了100位居民某年的月均用水量(单位:吨)并对数据进行处理,得到该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏).
组号
分组
频数
频率
1
[0,0.5)
4
0.04
2
[0.5,1)
0.08
3
[1,1.5)
15
4
[1.5,2)
22
5
[2,2.5)
x
6
[2.5,3)
14
0.14
7
[3,3.5)
6
y
8
[3.5,4)
4
0.04
9
[4,4.5]
0.02
合计
100
(1)确定表中的x与y的值;
(2)在上述频率分布直方图中,求从左往右数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图.
解:(1)因为总数是100,区间[0.5,1)内的频率为0.08,区间[4,4.5)内的频率为0.02,
所以区间[0.5,1)内的频数为8,区间[4,4.5)内的频数为2.
则x=100-(4+8+15+22+14+6+4+2)=25,y=
=0.06.
(2)因为左数第4个矩形对应的频率为0.22,且表中的数据组距为0.5,
所以它的高度为0.22÷0.5=0.44.
(3)由频率分布直方图,画出折线图如图所示:
[A 基础达标]
1.某地农村2004年到2019年间人均居住面积的统计图如图所示,则增长最多的5年为( )
A.2004年~2009年
B.2009年~2014年
C.2014~2019年
D.无法从图中看出
解析:选C.2004年~2009年的增长量为3.1,2009年~2014年的增长量为3.2,2014年~2019年的增长量为3.8.
2.下面是两户居民家庭全年各项支出的统计图.
根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大
B.乙户比甲户大
C.甲、乙两户一样大
D.无法确定哪一户大
解析:选B.条形统计图反映具体数值,则由图甲可知,甲户教育支出占全年总支出的百分比为1
200÷(1
200+2
000+1
200+1
600)=20%;从扇形统计图乙可知,乙户教育支出占全年总支出的百分比为25%.所以乙户比甲户大.
3.为了解某地区高一学生身体发育情况,抽查了该地区100名年龄为17.5~18岁的男生体重(kg),得到频率分布直方图(如图所示).
可得这100名学生中体重在[56.5,64.5)的学生人数是( )
A.20
B.30
C.40
D.50
解析:选C.由频率分布直方图易得到体重在[56.5,64.5)的学生的频率为(0.03+0.05+0.05+0.07)×2=0.4,那么学生的人数为100×0.4=40,故选C.
4.某工厂对一批元件进行抽样检测,经检测,抽出的元件的长度(单位:mm)全部介于93至105之间.将抽出的元件的长度以2为组距分成6组:[93,95),[95,97),[97,99),[99,101),[101,103),[103,105],得到如图所示的频率分布直方图.若长度在[97,103)内的元件为合格品,根据频率分布直方图,估计这批元件的合格率是( )
A.80%
B.90%
C.20%
D.85.5%
解析:选A.由频率分布直方图可知元件长度在[97,103)内的频率为1-(0.027
5+0.027
5+0.045
0)×2=0.8,故这批元件的合格率为80%.
5.为了解电视对生活的影响,一个社会调查机构就平均每天看电视的时间调查了某地10
000位居民,并根据所得数据画出样本的频率分布直方图(如图),为了分析该地居民平均每天看电视的时间与年龄、学历、职业等方面的关系,要从这10
000位居民中再用分层抽样抽出100位居民做进一步调查,则[2.5,3)(小时)时间段内应抽出的人数是( )
A.25
B.30
C.50
D.75
解析:选A.抽出的100位居民中平均每天看电视的时间在[2.5,3)(小时)时间内的频率为0.5×0.5=0.25,所以这10
000位居民中平均每天看电视的时间在[2.5,3)(小时)时间内的人数是10
000×0.25=2
500.依题意知抽样比是=,则在[2.5,3)(小时)时间段内应抽出的人数是2
500×=25.
6.巴西世界杯足球赛门票面向全球发行时,某售票窗口在3月1日至8日的售票情况如图所示,由图可知,售票最多的日期是__________;售票最少的日期是__________;前4天共售票为__________张.
解析:由题图可知,售票最多的日期是3月2日;最少的日期是3月3日与3月7日;前4天共售票8+14+7+12=41(张).
答案:3月2日 3月3日与3月7日 41
7.某校为了了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用如图所示的条形图表示.根据条形图可得这50名学生这一天平均每人的睡眠时间为______h.
解析:法一:要确定这50名学生的平均睡眠时间,就必须计算其总睡眠时间.总睡眠时间为5.5×0.1×50+6×0.3×50+6.5×0.4×50+7×0.1×50+7.5×0.1×50=27.5+90+130+35+37.5=320.
故平均睡眠时间为320÷50=6.4(h).
法二:根据图形得平均每人的睡眠时间为
t=5.5×0.1+6×0.3+6.5×0.4+7×0.1+7.5×0.1=6.4(h).
答案:6.4
8.某地为了了解该地区10
000户家庭的用电情况,采用分层随机抽样的方法抽取了500户家庭的月平均用电量,并根据这500户家庭的月平均用电量画出频率分布直方图如图所示,则该地区10
000户家庭中月平均用电度数在[70,80)的家庭有______户.
解析:根据频率分布直方图得该地区10
000户家庭中月平均用电度数在[70,80)的家庭有10
000×0.012×10=1
200
(户).
答案:1
200
9.为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示:
分组(单位:岁)
频数
频率
[20,25)
5
0.05
[25,30)
①
0.20
[30,35)
35
②
[35,40)
30
0.30
[40,45]
10
0.10
合计
100
1.00
(1)频率分布表中的①②位置应填什么数据?
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数.
解:(1)设年龄在[25,30)岁的频数为x,年龄在[30,35)岁的频率为y.
法一:根据题意可得=0.20,=y,
解得x=20,y=0.35,故①处应填20,②处应填0.35.
法二:由题意得5+x+35+30+10=100,
0.05+0.20+y+0.30+0.10=1,
解得x=20,y=0.35,故①处填20,②处填0.35.
(2)由频率分布表知年龄在[25,30)岁的频率是0.20,组距是5.
所以==0.04.
补全频率分布直方图如图所示.
根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数为500×0.35=175.
10.为了了解学生参加体育活动的情况,某校对学生进行了随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项可供选择:
A.1.5小时以上
B.1~1.5小时
C.0.5~1小时
D.0.5小时以下
下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图中提供的信息解答以下问题:
(1)本次一共调查了多少名学生;
(2)在图(1)中将选项B对应的部分补充完整;
(3)若该校有3
000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
解:(1)由图(1)知,选A的人数为60,而图(2)显示,选A的人数占总人数的30%,故本次调查的总人数为60÷30%=200.
(2)由图(2)知,选B的人数占总人数的50%,因此其人数为200×50%=100,图(1)补充如图所示:
(3)根据图(2)知:平均每天参加体育活动的时间在0.5小时以下的人数占统计人数的5%,以此估计得3
000×5%=150(人).
[B 能力提升]
11.在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其他7个小长方形的面积和的,且样本容量为200,则第8组的频数为______.
解析:设最后一个小长方形的面积为x,则其他7个小长方形的面积为4x,从而x+4x=1,所以x=0.2.故第8组的频数为200×0.2=40.
答案:40
12.90,92,92,93,93,94,95,96,99,100的75%分位数为______,80%分位数为______.
解析:10×75%=7.5,10×80%=8,
所以75%分位数为x8=96,
80%分位数为==97.5.
答案:96 97.5
13.(2019·山西省大同市铁路一中期末考试)为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
解析:根据图可知第四与第五组的频率和为(0.012
5+0.037
5)×5=0.25,
因为从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,
所以前三个小组的频数为36,从而男生有=48(人).
因为全校男、女生比例为3∶2,所以全校抽取学生数为48×=80.
答案:80
14.某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.
(1)求直方图中x的值;
(2)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层随机抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
解:(1)x=[1-(0.002+0.009
5+0.011+0.012
5+0.005+0.002
5)×20]÷20=0.007
5.
(2)由频率分布直方图知,月平均用电量为[220,240),[240,260),[260,280),[280,300]的共有[(0.012
5+0.007
5+0.005+0.002
5)×20]×100=55(户),其中在[220,240)中的有0.012
5×20×100=25(户),因此,在所抽取的11户居民中,月平均用电量在[220,240)的用户中应抽取×11=5(户).
[C 拓展探究]
15.某高校在2019年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下:
组号
分组
频数
频率
第1组
[160,165)
5
0.05
第2组
[165,170)
①
0.35
第3组
[170,175)
30
②
第4组
[175,180)
20
0.20
第5组
[180,185]
10
0.10
合计
100
1.00
(1)请先求出频率分布表中①②处应填写的数据,并完成如图所示的频率分布直方图;
(2)为了选拔出最优秀的学生,高校决定在笔试成绩高的第3,4,5组中用分层随机抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各应抽取多少名学生进入第二轮面试.
解:(1)由题意可知,第2组的频数为0.35×100=35,第3组的频率为=0.30,故①处填35,②处填0.30.
频率分布直方图如图所示.
(2)因为第3,4,5组共有60名学生,所以利用分层随机抽样在60名学生中抽取6名学生,抽样比为=,故第3组应抽取30×=3(名)学生,第4组应抽取20×=2(名)学生,第5组应抽取10×=1(名)学生,所以第3,4,5组应抽取的学生人数分别为3,2,1.
PAGE
9.2.1 总体取值规律的估计
9.2.2 总体百分位数的估计
考点
学习目标
核心素养
频率分布表、频率分布直方图
会画一组数据的频率分布表、频率分布直方图
直观想象、数据分析
用样本估计总体
会用频率分布表、频率分布直方图、条形图、扇形图、折线图等对总体进行估计
直观想象、数据分析
总体百分位数的估计
掌握求n个数据的第p百分位数的方法
数学抽象、数学运算
问题导学
预习教材P192-P202的内容,思考以下问题:
1.绘制频率分布表和频率分布直方图有哪些步骤?
2.频率分布直方图有哪些特征?
3.如何求n个数据的第p百分位数?
1.频率分布表、频率分布直方图的制作步骤及意义
2.百分位数
(1)定义:一般地,一组数据的第p百分位数是这样一个值,它使得这组数据中至少有p%的数据小于或等于这个值,且至少有(100-p)%的数据大于或等于这个值.
(2)计算步骤:计算一组n个数据的第p百分位数的步骤:
第1步,按从小到大排列原始数据.
第2步,计算i=n×p%.
第3步,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数.
判断(正确的打“√”,错误的打“×”)
(1)直方图的高表示取某数的频率.( )
(2)直方图的高表示该组上的个体在样本中出现的频率.( )
(3)直方图的高表示取某组上的个体在样本中出现的频数与组距的比值.( )
(4)直方图的高表示取该组上的个体在样本中出现的频率与组距的比值.( )
解析:要注意频率分布直方图的特点.在直方图中,纵轴(矩形的高)表示频率与组距的比值,其相应组距上的频率等于该组距上的矩形的面积.
答案:(1)× (2)× (3)× (4)√
一个容量为80的样本中数据的最大值是140,最小值是51,组距是10,则应将样本数据分为( )
A.10组
B.9组
C.8组
D.7组
解析:选B.极差为140-51=89,而组距为10,故应将样本数据分为9组.
将容量为100的样本数据按由小到大排列分成8个小组,如表所示,但第3组被墨汁污染,则第三组的频率为( )
组号
1
2
3
4
5
6
7
8
频数
10
13
14
15
13
12
9
A.0.14
B.0.12
C.0.03
D.0.10
解析:选A.第三组的频数为100-(10+13+14+15+13+12+9)=14.故第三组的频率为=0.14.
(2019·四川省绵阳市教学质量测试)某高速公路移动雷达测速检测车在某时段对某段路过往的400辆汽车的车速进行检测,根据检测的结果绘制出如图所示的频率分布直方图,根据直方图的数据估计400辆汽车中时速在区间[90,110)的约有____________辆.
解析:由图可知,时速在区间[80,90),[110,120)的频率为(0.01+0.02)×10=0.3,
所以时速在区间[90,110)的频率为1-0.3=0.7.
所以时速在区间[90,110)的车辆数为400×0.7=280.
答案:280
频率分布表、频率分布直方
图、频率分布折线图的绘制
角度一 频率分布表、频率分布直方图的绘制
为考查某校高二男生的体重,随机抽取44名高二男生,实测体重数据(单位:kg)如下:
57,61,57,57,58,57,61,54,68,51,49,64,50,48,65,52,56,46,54,49,51,47,55,55,54,42,51,56,55,51,54,51,60,62,43,55,56,61,52,69,64,46,54,48
将数据进行适当的分组,并画出相应的频率分布直方图和频率分布折线图.
【解】 以4为组距,列表如下:
分组
频率累计
频数
频率
[41.5,45.5)
2
0.045
5
[45.5,49.5)
7
0.159
1
[49.5,53.5)
8
0.181
8
[53.5,57.5)
16
0.363
6
[57.5,61.5)
5
0.113
6
[61.5,65.5)
4
0.090
9
[65.5,69.5)
2
0.045
5
频率分布直方图和频率分布折线图如图所示.
(1)在列频率分布表时,极差、组距、组数有如下关系:
①若为整数,则=组数;
②若不为整数,则的整数部分+1=组数.
(2)组距和组数的确定没有固定的标准,将数据分组时,组数力求合适,纵使数据的分布规律能较清楚地呈现出来,组数太多或太少,都会影响我们了解数据的分布情况,若样本容量不超过100,按照数据的多少常分为5~12组,一般样本量越大,所分组数越多.
角度二 频率分布直方图的应用
为了了解高一年级学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组的频数为12.
(1)第二小组的频率是多少?样本量是多少?
(2)若次数在110以上(含110次)为达标,则该校全体高一年级学生的达标率是多少?
(3)样本中不达标的学生人数是多少?
(4)第三组的频数是多少?
【解】 (1)频率分布直方图以面积的形式反映数据落在各小组内的频率大小,因此第二小组的频率为=0.08.
又因为第二小组的频率=,
所以样本容量===150.
(2)由直方图可估计该校高一年级学生的达标率为×100%=88%.
(3)由(1)(2)知达标率为88%,样本量为150,不达标的学生频率为1-0.88=0.12.
所以样本中不达标的学生人数为150×0.12=18(人).
(4)第三小组的频率为=0.34.
又因为样本量为150,
所以第三组的频数为150×0.34=51.
频率分布直方图的应用中的计算问题
(1)小长方形的面积=组距×=频率;
(2)各小长方形的面积之和等于1;
(3)=频率,此关系式的变形为=样本量,样本量×频率=频数.
某厂对一批产品进行抽样检测,如图是抽检产品净重(单位:克)的频率分布直方图,样本数据分组为[76,78),[78,80),…,[84,86].若这批产品有120个,估计其中净重大于或等于78克且小于84克的产品的个数是( )
A.12
B.18
C.25
D.90
解析:选D.净重大于或等于78克且小于84克的频率为(0.100+0.150+0.125)×2=0.75,所以在该范围内的产品个数为120×0.75=90.
条形统计图
为了丰富校园文化生活,某校计划在午间校园广播台播放“百家讲坛”的部分内容.为了了解学生的喜好,抽取若干名学生进行问卷调查(每人只选一项内容),整理调查结果,绘制统计图如图所示.
请根据统计图提供的信息回答以下问题:
(1)求抽取的学生数;
(2)若该校有3
000名学生,估计喜欢收听易中天《品三国》的学生人数;
(3)估计该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的百分比.
【解】 (1)从统计图上可以看出,
喜欢收听于丹析《庄子》的男生有20人,女生有10人;
喜欢收听《故宫博物院》的男生有30人,女生有15人;
喜欢收听于丹析《论语》的男生有30人,女生有38人;
喜欢收听易中天《品三国》的男生有64人,女生有42人;
喜欢收听刘心武评《红楼梦》的男生有6人,女生有45人.
所以抽取的学生数为20+10+30+15+30+38+64+42+6+45=300(人).
(2)喜欢收听易中天《品三国》的男生有64人,女生有42人,共有106人,占所抽取总人数的比例为,
由于该校有3
000名学生,因此可以估计喜欢收听易中天《品三国》的学生有×3
000=1
060(人).
(3)该校喜欢收听刘心武评《红楼梦》的女学生人数约占全校学生人数的比例为×100%=15%.
(1)绘制条形统计图时,第一步确定坐标系中横轴和纵轴上坐标的意义,第二步确定横轴上各部分的间距及位置,第三步根据统计结果绘制条形图.
实际问题中,我们需根据需要进行分组,横轴上的分组越细,对数据的刻画(描述)就越精确.
(2)在条形统计图中,各个矩形图的宽度没有严格要求,但高度必须以数据为准,它直观反映了各部分在总体中所占比重的大小.
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层随机抽样调查,测得身高情况的统计图如图所示.
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185
cm之间的学生占总人数的百分比是多少.
解:(1)样本中男生人数为40,由分层随机抽样比例为10%估计全校男生人数为400.
(2)由统计图知,样本身高在170~185
cm之间的学生有14+13+4+3+1=35(人),样本容量为70,所以在样本中学生身高在170~185
cm之间所占比例为=50%,故可估计该校学生身高在170~185
cm之间的学生占总人数的50%.
折线统计图
小明同学因发热而住院,下图是根据护士为他测量的体温所绘制的体温折线图.
根据图中的信息,回答以下问题:
(1)护士每隔几小时给小明测量一次体温?
(2)近三天来,小明的最高体温、最低体温分别是多少?
(3)从体温看,小明的病情是在恶化还是在好转?
(4)如果连续36小时体温不超过37.2摄氏度的话,可认为基本康复,那么小明最快什么出院?
【解】 (1)根据横轴表示的意义,可知护士每隔6小时给小明测量一次体温.
(2)从折线统计图中的最高点和最低点对应的纵轴意义,可知最高体温是39.5摄氏度,最低体温是36.8摄氏度.
(3)从图中可知小明的体温已经下降,并趋于稳定,因此病情在好转.
(4)9月8日18时小明的体温是37摄氏度.其后的体温未超过37.2摄氏度,自9月8日18时起计算,连续36小时后对应的时间为9月10日凌晨6时.因此小明最快可以在9月10凌晨6时出院.
(1)绘制折线统计图时,第一步,确定直角坐标系中横、纵坐标表示的意义;第二步,确定一个单位长度表示一定的数量,根据数量的多少描出各点;第三步,用直线段顺次连接即可.
(2)在折线统计图中,从折线的上升、下降可分析统计数量的增减变化情况,从陡峭程度上,可分析数据间相对增长、下降的幅度.
据报道,去年某咨询公司对1
500个家庭进行了关于奶粉市场的调查,下图是关于每月购买奶粉袋数的有关数据,则每月购买1袋奶粉的比率同每月购买2袋奶粉的比率合计为( )
A.79.9%
B.70.9%
C.38.8%
D.32.1%
解析:选B.根据折线图,每月购买1袋奶粉和每月购买2袋奶粉的比率分别为38.8%和32.1%,故所求为38.8%+32.1%=70.9%.
扇形统计图
下图是A,B两所学校艺术节期间收到的各类艺术作品的情况的统计图:
(1)从图中能否看出哪所学校收到的水粉画作品数量多?为什么?
(2)已知A学校收到的剪纸作品比B学校的多20件,收到的书法作品比B学校的少100件,请问这两所学校收到艺术作品的总数分别是多少件?
【解】 (1)不能.因为两所学校收到艺术作品的总数不知道.
(2)设A学校收到艺术作品的总数为x件,B学校收到艺术作品的总数为y件,则解得即A学校收到艺术作品的总数为500件,B学校收到艺术作品的总数为600件.
(1)绘制扇形统计图时,第一步计算各部分所占百分比以及对应圆心角的度数;第二步在圆中按照上述圆心角画出各个扇形并恰当标注.
(2)扇形统计图表示总体的各部分之间的百分比关系,但不同总量下的扇形统计图,其不同的百分比不可以作为比较的依据.
如图是2019年各级学校每10万人口中平均在校生的人数扇形统计图,则下列结论正确的是( )
A.2019年有6%的高中生升入高等学校
B.2019年全国高等学校在校生6
000人
C.2019年各级学校10万人口平均在校生数在高等学校学生中占6%
D.2019年高等学校的学生比高中阶段的学生多
解析:选C.由扇形统计图可以看出,2019年各级学校每10万人口中平均在校生的人数所占的百分比分别为幼儿园占8%,高等学校占6%,高中阶段占12%,初中阶段占26%,小学占48%,A项中应是高等学校在校学生.B项中6
000人应是平均数,D项显然错误.
百分位数的计算
现有甲、乙两组数据如下表所示.
序号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
甲组
1
2
2
2
2
3
3
3
5
5
6
6
8
8
9
10
10
12
13
13
乙组
0
0
0
0
1
1
2
3
4
5
6
6
7
7
10
14
14
14
14
15
试求甲、乙两组数的25%分位数与75%分位数.
【解】 因为数据个数为20,而且20×25%=5,20×75%=15.
因此,甲组数的25%分位数为==2.5;
甲组数的75%分位数为==9.5.
乙组数的25%分位数为==1,乙组的75%分位数为==12.
求百分位数时,一定要将数据按照从小到大的顺序排列.
求1,2,3,4,5,6,7,8,9,10的25%分位数,75%分位数,90%分位数.
解:因为数据个数为10,而且10×25%=2.5,10×75%=7.5,10×90%=9.
所以该组数据的25%分位数为x3=3,75%分位数为x8=8,90%分位数为==9.5.
1.下列四个图中,用来表示不同品种的奶牛的平均产奶量最为合适的是( )
解析:选D.用统计图表示不同品种的奶牛的平均产奶量,即从图中可以比较各种数量的多少,因此“最为合适”的统计图是条形统计图.注意B选项中的图不能称为统计图.
2.观察新生儿的体重,其频率分布直方图如图所示,则新生儿体重在[2
700,3
000)g的频率为( )
A.0.1
B.0.2
C.0.3
D.0.4
解析:选C.由题图可得,新生儿体重在[2
700,3
000)g的频率为0.001×300=0.3,故选C.
3.观察下图所示的统计图,下列结论正确的是( )
A.甲校女生比乙校女生多
B.乙校男生比甲校男生少
C.乙校女生比甲校男生少
D.甲、乙两校女生人数无法比较
解析:选D.图中数据只是百分比,甲、乙两个学校的学生总数不知道,因此男生与女生的具体人数也无法得知.
4.(2019·广西钦州市期末考试)为了了解某城市居民用水量情况,我们抽取了100位居民某年的月均用水量(单位:吨)并对数据进行处理,得到该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏).
组号
分组
频数
频率
1
[0,0.5)
4
0.04
2
[0.5,1)
0.08
3
[1,1.5)
15
4
[1.5,2)
22
5
[2,2.5)
x
6
[2.5,3)
14
0.14
7
[3,3.5)
6
y
8
[3.5,4)
4
0.04
9
[4,4.5]
0.02
合计
100
(1)确定表中的x与y的值;
(2)在上述频率分布直方图中,求从左往右数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图.
解:(1)因为总数是100,区间[0.5,1)内的频率为0.08,区间[4,4.5)内的频率为0.02,
所以区间[0.5,1)内的频数为8,区间[4,4.5)内的频数为2.
则x=100-(4+8+15+22+14+6+4+2)=25,y=
=0.06.
(2)因为左数第4个矩形对应的频率为0.22,且表中的数据组距为0.5,
所以它的高度为0.22÷0.5=0.44.
(3)由频率分布直方图,画出折线图如图所示:
[A 基础达标]
1.某地农村2004年到2019年间人均居住面积的统计图如图所示,则增长最多的5年为( )
A.2004年~2009年
B.2009年~2014年
C.2014~2019年
D.无法从图中看出
解析:选C.2004年~2009年的增长量为3.1,2009年~2014年的增长量为3.2,2014年~2019年的增长量为3.8.
2.下面是两户居民家庭全年各项支出的统计图.
根据统计图,下列对两户教育支出占全年总支出的百分比作出的判断中,正确的是( )
A.甲户比乙户大
B.乙户比甲户大
C.甲、乙两户一样大
D.无法确定哪一户大
解析:选B.条形统计图反映具体数值,则由图甲可知,甲户教育支出占全年总支出的百分比为1
200÷(1
200+2
000+1
200+1
600)=20%;从扇形统计图乙可知,乙户教育支出占全年总支出的百分比为25%.所以乙户比甲户大.
3.为了解某地区高一学生身体发育情况,抽查了该地区100名年龄为17.5~18岁的男生体重(kg),得到频率分布直方图(如图所示).
可得这100名学生中体重在[56.5,64.5)的学生人数是( )
A.20
B.30
C.40
D.50
解析:选C.由频率分布直方图易得到体重在[56.5,64.5)的学生的频率为(0.03+0.05+0.05+0.07)×2=0.4,那么学生的人数为100×0.4=40,故选C.
4.某工厂对一批元件进行抽样检测,经检测,抽出的元件的长度(单位:mm)全部介于93至105之间.将抽出的元件的长度以2为组距分成6组:[93,95),[95,97),[97,99),[99,101),[101,103),[103,105],得到如图所示的频率分布直方图.若长度在[97,103)内的元件为合格品,根据频率分布直方图,估计这批元件的合格率是( )
A.80%
B.90%
C.20%
D.85.5%
解析:选A.由频率分布直方图可知元件长度在[97,103)内的频率为1-(0.027
5+0.027
5+0.045
0)×2=0.8,故这批元件的合格率为80%.
5.为了解电视对生活的影响,一个社会调查机构就平均每天看电视的时间调查了某地10
000位居民,并根据所得数据画出样本的频率分布直方图(如图),为了分析该地居民平均每天看电视的时间与年龄、学历、职业等方面的关系,要从这10
000位居民中再用分层抽样抽出100位居民做进一步调查,则[2.5,3)(小时)时间段内应抽出的人数是( )
A.25
B.30
C.50
D.75
解析:选A.抽出的100位居民中平均每天看电视的时间在[2.5,3)(小时)时间内的频率为0.5×0.5=0.25,所以这10
000位居民中平均每天看电视的时间在[2.5,3)(小时)时间内的人数是10
000×0.25=2
500.依题意知抽样比是=,则在[2.5,3)(小时)时间段内应抽出的人数是2
500×=25.
6.巴西世界杯足球赛门票面向全球发行时,某售票窗口在3月1日至8日的售票情况如图所示,由图可知,售票最多的日期是__________;售票最少的日期是__________;前4天共售票为__________张.
解析:由题图可知,售票最多的日期是3月2日;最少的日期是3月3日与3月7日;前4天共售票8+14+7+12=41(张).
答案:3月2日 3月3日与3月7日 41
7.某校为了了解学生的睡眠情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用如图所示的条形图表示.根据条形图可得这50名学生这一天平均每人的睡眠时间为______h.
解析:法一:要确定这50名学生的平均睡眠时间,就必须计算其总睡眠时间.总睡眠时间为5.5×0.1×50+6×0.3×50+6.5×0.4×50+7×0.1×50+7.5×0.1×50=27.5+90+130+35+37.5=320.
故平均睡眠时间为320÷50=6.4(h).
法二:根据图形得平均每人的睡眠时间为
t=5.5×0.1+6×0.3+6.5×0.4+7×0.1+7.5×0.1=6.4(h).
答案:6.4
8.某地为了了解该地区10
000户家庭的用电情况,采用分层随机抽样的方法抽取了500户家庭的月平均用电量,并根据这500户家庭的月平均用电量画出频率分布直方图如图所示,则该地区10
000户家庭中月平均用电度数在[70,80)的家庭有______户.
解析:根据频率分布直方图得该地区10
000户家庭中月平均用电度数在[70,80)的家庭有10
000×0.012×10=1
200
(户).
答案:1
200
9.为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示:
分组(单位:岁)
频数
频率
[20,25)
5
0.05
[25,30)
①
0.20
[30,35)
35
②
[35,40)
30
0.30
[40,45]
10
0.10
合计
100
1.00
(1)频率分布表中的①②位置应填什么数据?
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数.
解:(1)设年龄在[25,30)岁的频数为x,年龄在[30,35)岁的频率为y.
法一:根据题意可得=0.20,=y,
解得x=20,y=0.35,故①处应填20,②处应填0.35.
法二:由题意得5+x+35+30+10=100,
0.05+0.20+y+0.30+0.10=1,
解得x=20,y=0.35,故①处填20,②处填0.35.
(2)由频率分布表知年龄在[25,30)岁的频率是0.20,组距是5.
所以==0.04.
补全频率分布直方图如图所示.
根据频率分布直方图估计这500名志愿者中年龄在[30,35)岁的人数为500×0.35=175.
10.为了了解学生参加体育活动的情况,某校对学生进行了随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项可供选择:
A.1.5小时以上
B.1~1.5小时
C.0.5~1小时
D.0.5小时以下
下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图中提供的信息解答以下问题:
(1)本次一共调查了多少名学生;
(2)在图(1)中将选项B对应的部分补充完整;
(3)若该校有3
000名学生,你估计全校有多少名学生平均每天参加体育活动的时间在0.5小时以下?
解:(1)由图(1)知,选A的人数为60,而图(2)显示,选A的人数占总人数的30%,故本次调查的总人数为60÷30%=200.
(2)由图(2)知,选B的人数占总人数的50%,因此其人数为200×50%=100,图(1)补充如图所示:
(3)根据图(2)知:平均每天参加体育活动的时间在0.5小时以下的人数占统计人数的5%,以此估计得3
000×5%=150(人).
[B 能力提升]
11.在样本的频率分布直方图中,共有8个小长方形,若最后一个小长方形的面积等于其他7个小长方形的面积和的,且样本容量为200,则第8组的频数为______.
解析:设最后一个小长方形的面积为x,则其他7个小长方形的面积为4x,从而x+4x=1,所以x=0.2.故第8组的频数为200×0.2=40.
答案:40
12.90,92,92,93,93,94,95,96,99,100的75%分位数为______,80%分位数为______.
解析:10×75%=7.5,10×80%=8,
所以75%分位数为x8=96,
80%分位数为==97.5.
答案:96 97.5
13.(2019·山西省大同市铁路一中期末考试)为了解某校高三学生的身体状况,用分层随机抽样的方法抽取部分男生和女生的体重,将男生体重数据整理后,画出了频率分布直方图,已知图中从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,若全校男、女生比例为3∶2,则全校抽取学生数为________.
解析:根据图可知第四与第五组的频率和为(0.012
5+0.037
5)×5=0.25,
因为从左到右前三个小组频率之比为1∶2∶3,第二小组频数为12,
所以前三个小组的频数为36,从而男生有=48(人).
因为全校男、女生比例为3∶2,所以全校抽取学生数为48×=80.
答案:80
14.某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.
(1)求直方图中x的值;
(2)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层随机抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
解:(1)x=[1-(0.002+0.009
5+0.011+0.012
5+0.005+0.002
5)×20]÷20=0.007
5.
(2)由频率分布直方图知,月平均用电量为[220,240),[240,260),[260,280),[280,300]的共有[(0.012
5+0.007
5+0.005+0.002
5)×20]×100=55(户),其中在[220,240)中的有0.012
5×20×100=25(户),因此,在所抽取的11户居民中,月平均用电量在[220,240)的用户中应抽取×11=5(户).
[C 拓展探究]
15.某高校在2019年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下:
组号
分组
频数
频率
第1组
[160,165)
5
0.05
第2组
[165,170)
①
0.35
第3组
[170,175)
30
②
第4组
[175,180)
20
0.20
第5组
[180,185]
10
0.10
合计
100
1.00
(1)请先求出频率分布表中①②处应填写的数据,并完成如图所示的频率分布直方图;
(2)为了选拔出最优秀的学生,高校决定在笔试成绩高的第3,4,5组中用分层随机抽样的方法抽取6名学生进入第二轮面试,求第3,4,5组每组各应抽取多少名学生进入第二轮面试.
解:(1)由题意可知,第2组的频数为0.35×100=35,第3组的频率为=0.30,故①处填35,②处填0.30.
频率分布直方图如图所示.
(2)因为第3,4,5组共有60名学生,所以利用分层随机抽样在60名学生中抽取6名学生,抽样比为=,故第3组应抽取30×=3(名)学生,第4组应抽取20×=2(名)学生,第5组应抽取10×=1(名)学生,所以第3,4,5组应抽取的学生人数分别为3,2,1.
PAGE
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
