京改版九年级数学上册19.4.3《二次函数的应用(3)》教案
文档属性
| 名称 | 京改版九年级数学上册19.4.3《二次函数的应用(3)》教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 113.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 18:41:47 | ||
图片预览


文档简介
北京版九年级数学上册
第19章 二次函数和反比例函数
19.4《二次函数的应用(3)》教案
教学目标
一、知识与技能
1. 通过自主学习和合作探究,使学生经历探索商品销售中最大利润等问题的过程,列出函数关系式,感受二次函数的应用价值.
2. 通过巩固与运用,让学生能够分析和表示商品销售中变量之间的函数关系,并运用二次函数的性质求出实际问题的极值,增强解决问题的能力.
二、知识与能力
采用自主、合作、探究的学习方法,引导学生学会探究利用二次函数解决与利润有关的实际问题,进一步体会应用用二次函数顶点公式解决实际问题,通过对生活中实际问题的探究,体会数学建模思想.
三、情感态度与价值观
通过学习、理解和运用,让学生从实际问题中学会利用二次函数解决与利润有关的实际问题,体会运用二次函数顶点公式求极值的便利性,增强数学建模思想,促进综合素质的提高.
教学重点
能够分析和表示商品销售中变量之间的函数关系,运用二次函数的性质求出实际问题的极值,.
教学难点
分析和表示实际问题中变量之间的二次函数关系,正确地列出二次函数关系式.
教学过程
一、知识回顾
1、求下列二次函数的最大值或最小值:
⑴ y=-x2+2x-3; ⑵ y=x2+4x
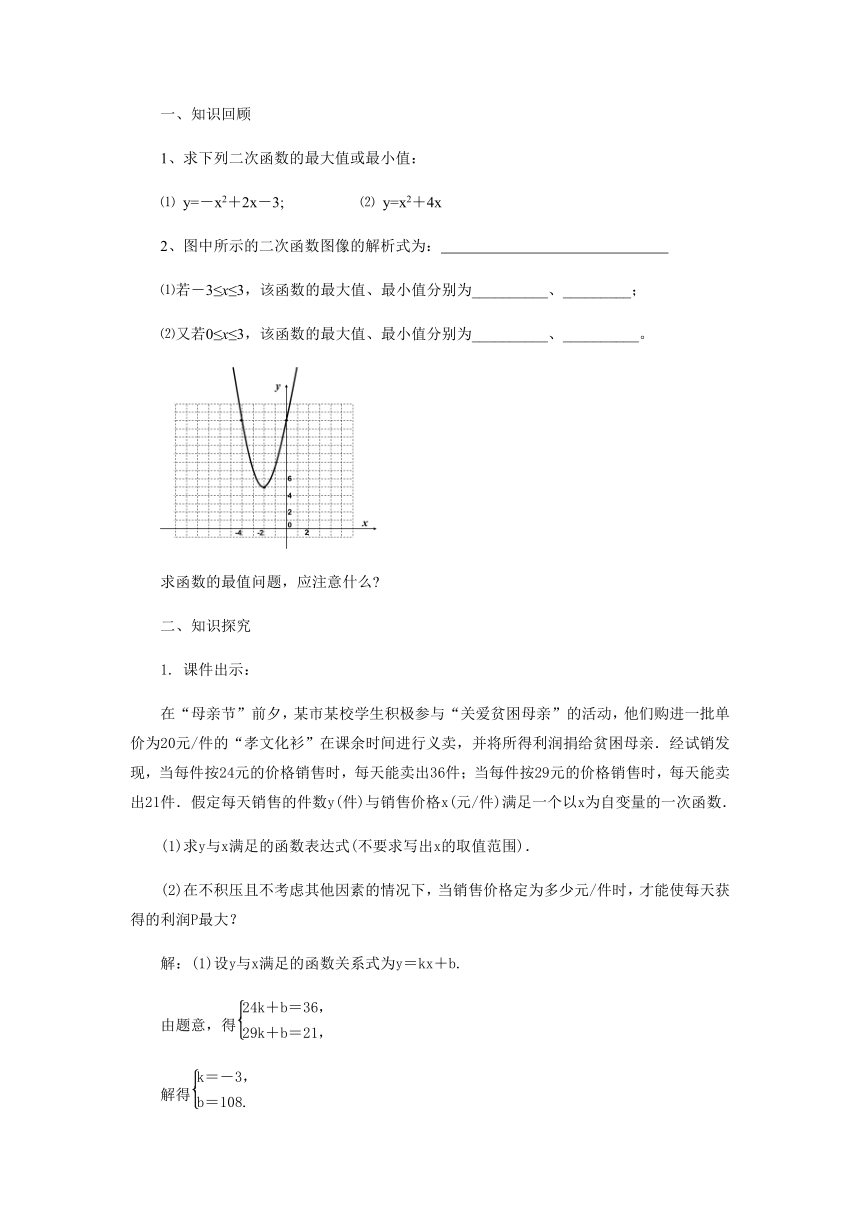
2、图中所示的二次函数图像的解析式为:
⑴若-3≤x≤3,该函数的最大值、最小值分别为__________、_________;
⑵又若0≤x≤3,该函数的最大值、最小值分别为__________、__________。
求函数的最值问题,应注意什么?
二、知识探究
1. 课件出示:
在“母亲节”前夕,某市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元/件的“孝文化衫”在课余时间进行义卖,并将所得利润捐给贫困母亲.经试销发现,当每件按24元的价格销售时,每天能卖出36件;当每件按29元的价格销售时,每天能卖出21件.假定每天销售的件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数表达式(不要求写出x的取值范围).
(2)在不积压且不考虑其他因素的情况下,当销售价格定为多少元/件时,才能使每天获得的利润P最大?
解:(1)设y与x满足的函数关系式为y=kx+b.
由题意,得
解得
∴y与x的函数关系式为y=-3x+108.
(2)由题意,得每天获得的利润
P=(-3x+108)·(x-20)=-3(x-28)2+192.
∵a=-3<0,∴当x=28时,利润最大,
∴当销售价定为28元/件时,每天获得的利润最大.
2.课件出示:
某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.关于销售单价、日销售量、日销售利润的几组对应值如下表:
销售单价x(元) 85 95 105 115
日销售量y(个) 175 125 75 m
日销售利润w(元) 875 1875 1875 875
[注:日销售利润=日销售量×(销售单价-成本)]
(1)求y关于x的函数表达式(不要求写出x的取值范围)及m的值.
(2)根据以上信息,填空:
该产品的成本是 元/个,当销售单价x= 元/个时,日销售利润w最大,最大值是 元.
(3)公司计划开展科技创新,以降低该产品的成本.预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.要想实现销售单价为90元/个时,日销售利润不低于3 750元的销售目标,该产品的成本应不超过多少元/个?
解:(1)设y关于x的函数表达式为y=kx+b.
由题意可知,解得
∴y关于x的函数表达式为y=-5x+600.
当x=115时,m=-5×115+600=25.
(2)设该产品的成本是a元/个.
当x=85时,875=175×(85-a),解得a=80.
由题意知,w=(-5x+600)(x-80)=-5(x-100)2+2 000,
∴当x=100时,w有最大值,最大值为2 000.
(3)设科技创新后该产品的成本是b元/个.
当x=90时,(-5×90+600)(90-b)≥3 750,
解得b≤65.
答:该产品的成本应不超过65元/个.
四、例题精析
例1 还记得本章一开始的“种多少棵橙子树”的问题吗?我们得到表示增种橙子树的数量x(棵)与橙子总产量y(个)的二次函数表达式y=(600-5x)(100+x)=-5x2+100x+60 000.
我们还曾经利用列表的方法得到一个猜测,现在验证一下你的猜测是否正确?你是怎么做的?与同伴进行交流.
因为表达式是二次函数,所以求橙子的总产量y的最大值即是求函数的最大值.
所以y=-5x2+100x+60 000
=-5(x2-20x+100-100)+60 000
=-5(x-10)2+60 500
当x=10时,y最大=60 500.
(1)利用函数图象描述橙子的总产量与增种橙子树的棵数之间的关系.
(2)增种多少棵橙子树,可以使橙子的总产量在60 400个以上?
①当x<10时,橙子的总产量随增种橙子树的增加而增加;当x>10时,橙子的总产量随增种橙子树的增加而减小.
②由图可知,增种6棵、7棵、8棵、9棵、10棵、11棵、12棵、13棵或14棵,都可以使橙子总产量在60 400个以上.
例2 已知一个矩形的周长是24 cm.
(1)写出这个矩形的面积S与一边长a的函数表达式;
(2)画出这个函数的图象;
(3)当a长多少时,S最大?
解:(1)S=a(12-a)
=-a2+12a
=-(a2-12a+36-36)
=-(a-6)2+36.
(2)图象如下:
(3)当a=6时,S最大=36.
五、当堂训练
1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
2. 某商场以每件42元的价钱购进一种服装,根据试销得知这种服装每天的销售量t(件)与每件的销售价x(元/件)可看成是一次函数关系:t=-3x+204。
(1).写出商场卖这种服装每天销售利y(元)与每件的销售价x(元)间的函数关系式;
(2).通过对所得函数关系式进行配方,指出 商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适?最大利润为多少?
3. 某个商店的老板,他最近进了价格为30元的书包。起初以40元每个售出,平均每个月能售出200个。后来,根据市场调查发现:这种书包的售价每上涨1元,每个月就少卖出10个。现在请你帮帮他.
(1).如何定价才使他的利润最大?
(2).如何定价才使他的利润达到2160元?
七、课堂小结
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
1. 求出函数解析式和自变量的取值范围
2. 配方变形,或利用公式求它的最大值或最小值。
3. 检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内 。
八、布置作业
完成课本练习题.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
