六年级数学下册课件 - - 6.2.1 图形的认识与测量——立体图形 -人教新课标(共21张PPT)
文档属性
| 名称 | 六年级数学下册课件 - - 6.2.1 图形的认识与测量——立体图形 -人教新课标(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 11:17:09 | ||
图片预览





文档简介
(共21张PPT)
立体图形体积的复习
物体所占空间的大小,叫做物体的体积。
容器所能容纳物体的体积,叫做容积。
【学习目标】
1.我能理解并掌握立体图形体积计算公式及推导进程。
2.我能正确运用公式进行有关计算。
3.我能应用所学知识解决生活中的实际问题。
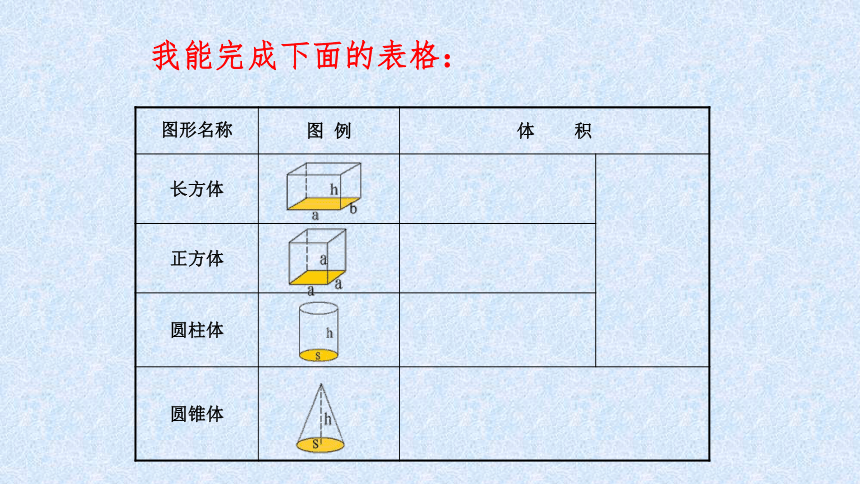
图形名称 图 例 体 积
长方体
正方体
圆柱体
圆锥体
我能完成下面的表格:
1.这些立体图形体积公式是怎样推导出来的?
2.这些公式之间有没有什么内在联系?
3.在解决有关立体图形体积的问题时,需要特别注意的地方是什么?
小组群学:
图形名称 图 例 体 积
长方体
正方体
圆柱体
圆锥体
V正=a3
V柱=Sh
V=Sh
V长=abh
我能完成下面的表格:
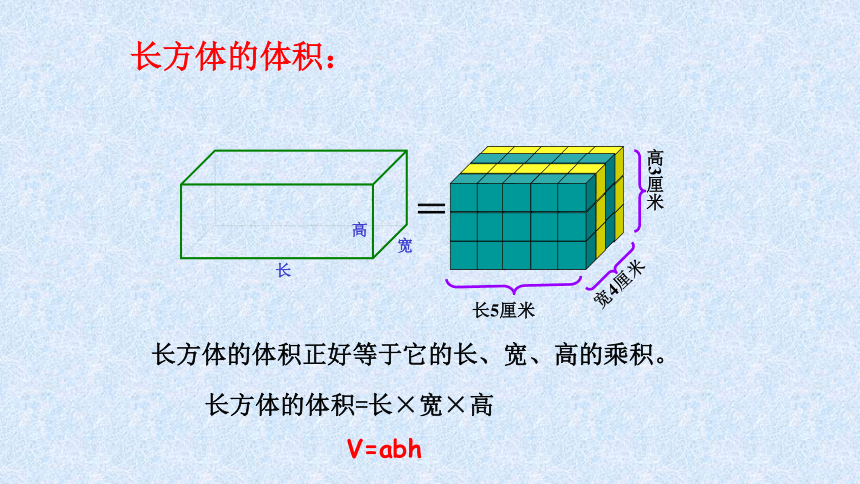
长5厘米
宽4厘米
高3厘米
长方体的体积正好等于它的长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
长方体的体积:
长
宽
高
=
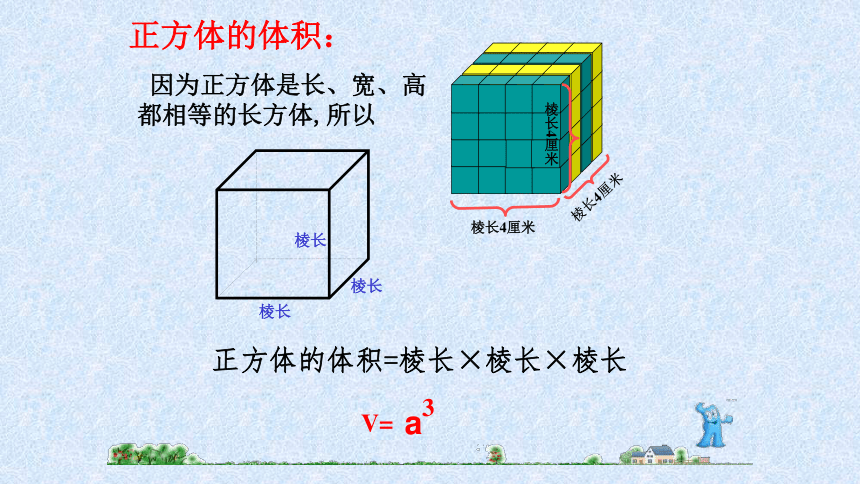
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
3
a
正方体的体积:
棱长
棱长
棱长
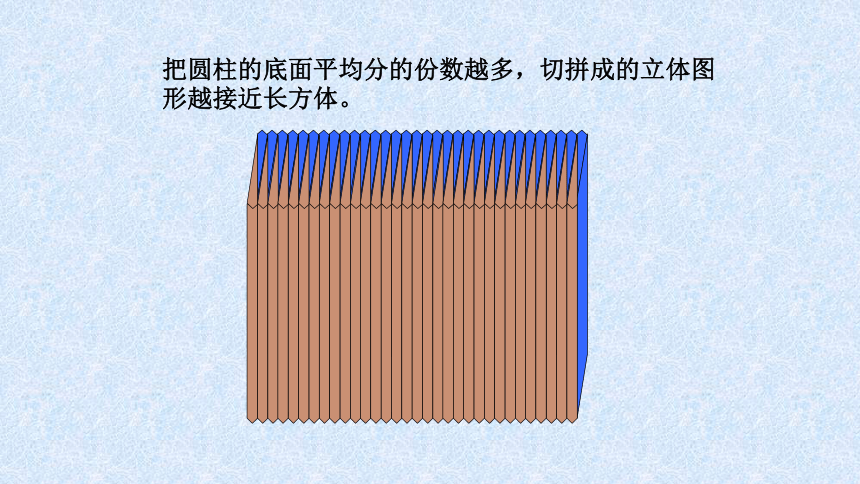
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
长方体体积=底面积×高
圆柱体积
=
=底面积×高
长方体的底面积等于圆柱的 底面积 ,
高等于圆柱的 高 。
V=Sh
圆柱的体积:
V=Sh
我能求出下面各图形的体积。(单位:cm)
(一)我能填:
4立方分米=( )立方厘米
0.3升=( )毫升=( )立方厘米
2. 20个1立方厘米的小正方体拼成一个长方体,这个长方体的体积是( )立方厘米。
3.一个正方体的棱长总和是24厘米,它的体积是( )立方厘米。
4.一个长方体的底面积是4平方分米,高是0.2米,它的体积是
( )立方分米。
5.一个圆柱底面半径是1厘米,高3厘米,它的体积是( )立方厘米,与它等底等高的圆锥体积是( )立方厘米。
6.一个圆锥的体积是30cm ,底面积是9cm ,高是( )。
4000
300
300
0.8
9.42
3.14
10cm
20
8
(二)我能解决下面的问题。
1. 一个长方体,长是12厘米,宽是6厘米,高是10厘米。
(1)长方体的体积是多少?
(2)切成最大的正方体, 正方体的体积是多少?
(3)将正方体切成最大的圆柱,圆柱的体积是多少?
(4)将圆柱削成最大的圆锥,圆锥的体积是多少?
2. 把一块棱长是8dm的正方形钢坯,锻造成一个长10 dm,宽4dm的长方体,这个长方体铁块的高是多少?
答:这个长方体铁块的高是12.8dm。
3. 把一个直角边分别为2厘米和3厘米的三角形,以一条直角边为轴旋转一周,想象一下,旋转起来的图形是什么形状?你能求出它的体积吗?
4. 一块长方形铁皮,长5分米,宽
3分米,像右图那样从4个角剪掉边
长是0.5分米的正方形,然后做成盒
子。这个盒子的容积有多少升?
5. 一个圆柱形容器的底面直径是10厘米,把一个马铃薯从在圆柱形的水中取出,水面下降了3厘米,一个马铃薯的体积是多少立方厘米?
五、解决生活中的实际问题。
这里有一瓶容积为1.5L的矿泉水,喝掉了一部分矿泉水,不借助其
它容器,你能想办法求出喝掉的
矿泉水的体积吗?
这节课你最大的收获或最深的感受是什么?还有什么疑问?
立体图形体积的复习
物体所占空间的大小,叫做物体的体积。
容器所能容纳物体的体积,叫做容积。
【学习目标】
1.我能理解并掌握立体图形体积计算公式及推导进程。
2.我能正确运用公式进行有关计算。
3.我能应用所学知识解决生活中的实际问题。
图形名称 图 例 体 积
长方体
正方体
圆柱体
圆锥体
我能完成下面的表格:
1.这些立体图形体积公式是怎样推导出来的?
2.这些公式之间有没有什么内在联系?
3.在解决有关立体图形体积的问题时,需要特别注意的地方是什么?
小组群学:
图形名称 图 例 体 积
长方体
正方体
圆柱体
圆锥体
V正=a3
V柱=Sh
V=Sh
V长=abh
我能完成下面的表格:
长5厘米
宽4厘米
高3厘米
长方体的体积正好等于它的长、宽、高的乘积。
长方体的体积=长×宽×高
V=abh
长方体的体积:
长
宽
高
=
棱长4厘米
棱长4厘米
棱长4厘米
因为正方体是长、宽、高都相等的长方体,所以
正方体的体积=棱长×棱长×棱长
V=
3
a
正方体的体积:
棱长
棱长
棱长
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
长方体体积=底面积×高
圆柱体积
=
=底面积×高
长方体的底面积等于圆柱的 底面积 ,
高等于圆柱的 高 。
V=Sh
圆柱的体积:
V=Sh
我能求出下面各图形的体积。(单位:cm)
(一)我能填:
4立方分米=( )立方厘米
0.3升=( )毫升=( )立方厘米
2. 20个1立方厘米的小正方体拼成一个长方体,这个长方体的体积是( )立方厘米。
3.一个正方体的棱长总和是24厘米,它的体积是( )立方厘米。
4.一个长方体的底面积是4平方分米,高是0.2米,它的体积是
( )立方分米。
5.一个圆柱底面半径是1厘米,高3厘米,它的体积是( )立方厘米,与它等底等高的圆锥体积是( )立方厘米。
6.一个圆锥的体积是30cm ,底面积是9cm ,高是( )。
4000
300
300
0.8
9.42
3.14
10cm
20
8
(二)我能解决下面的问题。
1. 一个长方体,长是12厘米,宽是6厘米,高是10厘米。
(1)长方体的体积是多少?
(2)切成最大的正方体, 正方体的体积是多少?
(3)将正方体切成最大的圆柱,圆柱的体积是多少?
(4)将圆柱削成最大的圆锥,圆锥的体积是多少?
2. 把一块棱长是8dm的正方形钢坯,锻造成一个长10 dm,宽4dm的长方体,这个长方体铁块的高是多少?
答:这个长方体铁块的高是12.8dm。
3. 把一个直角边分别为2厘米和3厘米的三角形,以一条直角边为轴旋转一周,想象一下,旋转起来的图形是什么形状?你能求出它的体积吗?
4. 一块长方形铁皮,长5分米,宽
3分米,像右图那样从4个角剪掉边
长是0.5分米的正方形,然后做成盒
子。这个盒子的容积有多少升?
5. 一个圆柱形容器的底面直径是10厘米,把一个马铃薯从在圆柱形的水中取出,水面下降了3厘米,一个马铃薯的体积是多少立方厘米?
五、解决生活中的实际问题。
这里有一瓶容积为1.5L的矿泉水,喝掉了一部分矿泉水,不借助其
它容器,你能想办法求出喝掉的
矿泉水的体积吗?
这节课你最大的收获或最深的感受是什么?还有什么疑问?
