人教八下数学17.1勾股定理教学设计
图片预览


文档简介
??教案准备
1.??教案目标
1.1 知识与技能:
通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论.
1.2 过程与方法:
1.在充分观察、归纳、猜想、探索直角三角形两条直角边的平方和等于斜边的平方的过程中,发展合情推理能力,体会数形结合的思想.
2.在探索上述结论的过程中,发展归纳、概括和有条理地表达活动的过程和结论.
1.3情感态度与价值观:
1.树立积极参与、合作交流的意识.
2.在探索勾股定理的过程中,体验获得结论的快乐,锻炼克服困难的勇气.
2.??教案重点/难点
2.1 教案重点:
探索直角三角形两条直角边的平方和等于斜边的平方的结论,从而发现勾股定理.
2.2 教案难点:
以直角三角形的边为边的正方形面积的计算.
3.??教案用具
4.??标签
??教案过程
1?谈话引入
我们知道,研究三角形从它的元素入手,也就是三角形的三条边和三个角。对于等腰三角形和等边三角形的边,除满足三边关系定理外,它们还分别存在着两边相等和三边相等的特殊关系。那么对于直角三角形的边,除满足三边关系定理外,它们之间也存在着特殊的关系,这就是我们这一节要研究的问题:勾股定理.
推进新课
(板书课题:勾股定理)
2?新知探究
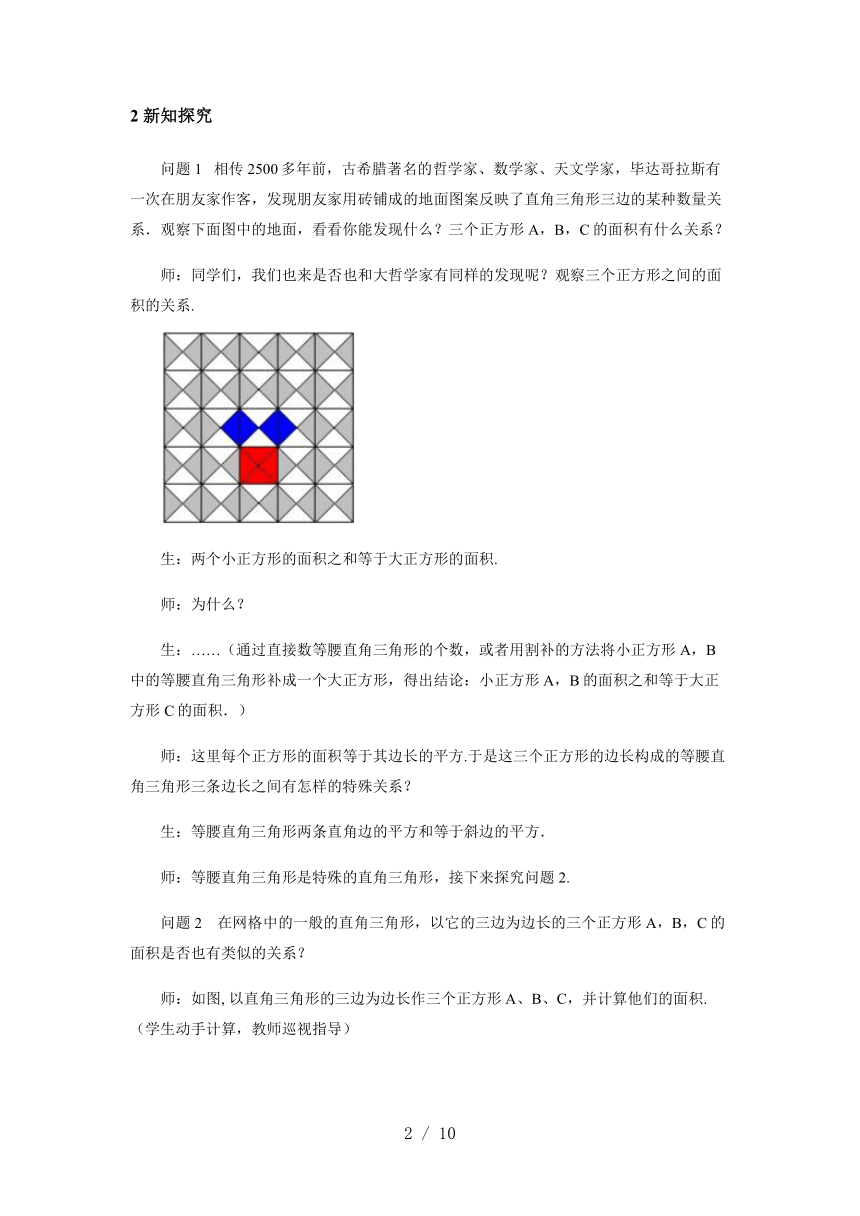
问题1???相传2500多年前,古希腊著名的哲学家、数学家、天文学家,毕达哥拉斯有一次在朋友家作客,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.观察下面图中的地面,看看你能发现什么?三个正方形A,B,C的面积有什么关系?
师:同学们,我们也来是否也和大哲学家有同样的发现呢?观察三个正方形之间的面积的关系.
生:两个小正方形的面积之和等于大正方形的面积.
师:为什么?
生:……(通过直接数等腰直角三角形的个数,或者用割补的方法将小正方形A,B中的等腰直角三角形补成一个大正方形,得出结论:小正方形A,B的面积之和等于大正方形C的面积.)
师:这里每个正方形的面积等于其边长的平方.于是这三个正方形的边长构成的等腰直角三角形三条边长之间有怎样的特殊关系?
生:等腰直角三角形两条直角边的平方和等于斜边的平方.
师:等腰直角三角形是特殊的直角三角形,接下来探究问题2.
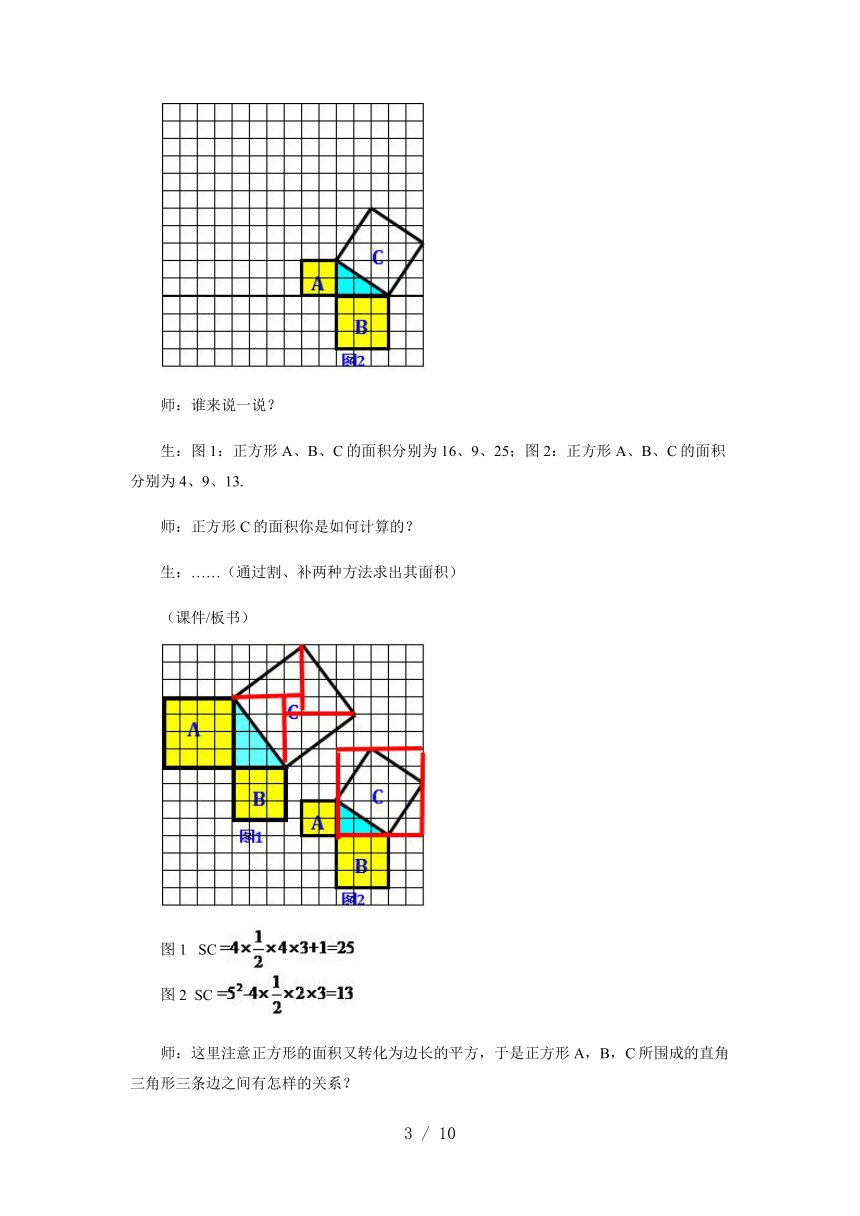
问题2 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C的面积是否也有类似的关系?
师:如图,?以直角三角形的三边为边长作三个正方形A、B、C,并计算他们的面积.(学生动手计算,教师巡视指导)
师:谁来说一说?
生:图1:正方形A、B、C的面积分别为16、9、25;图2:正方形A、B、C的面积分别为4、9、13.
师:正方形C的面积你是如何计算的?
生:……(通过割、补两种方法求出其面积)
(课件/板书)
图1???SC
图2??SC
师:这里注意正方形的面积又转化为边长的平方,于是正方形A,B,C所围成的直角三角形三条边之间有怎样的关系?
生:直角三角形两条直角边的平方和等于斜边的平方.
师:接下来我们来看问题3.
问题3??以上直角三角形的边长都是具体的数值,一般情况下,如果直角三角形的两直角边分别为a,b,斜边长为c,我们的猜想仍然成立吗?
师:这个结论仍然成立,中国人称它为“勾股定理”,外国人称它为“毕达哥拉斯定理”.
师:我国是最早发现勾股定理的国家之一,据《周髀算经》记载:公元前1100年人们已经知道“勾广三,股修四,径隅五”.?把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.?将此定理命名为勾股定理.
师:他有非常多证明方法,这里我们依然可以利用刚才的割补法.
(课件/板书)
“割”的方法:,于是.
“补”的方法:,于是.
(课件/板书)
勾股定理
直角三角形两直角边的平方和等于斜边的平方.?
师:请大家把这个结论一起来读两遍.(生读)
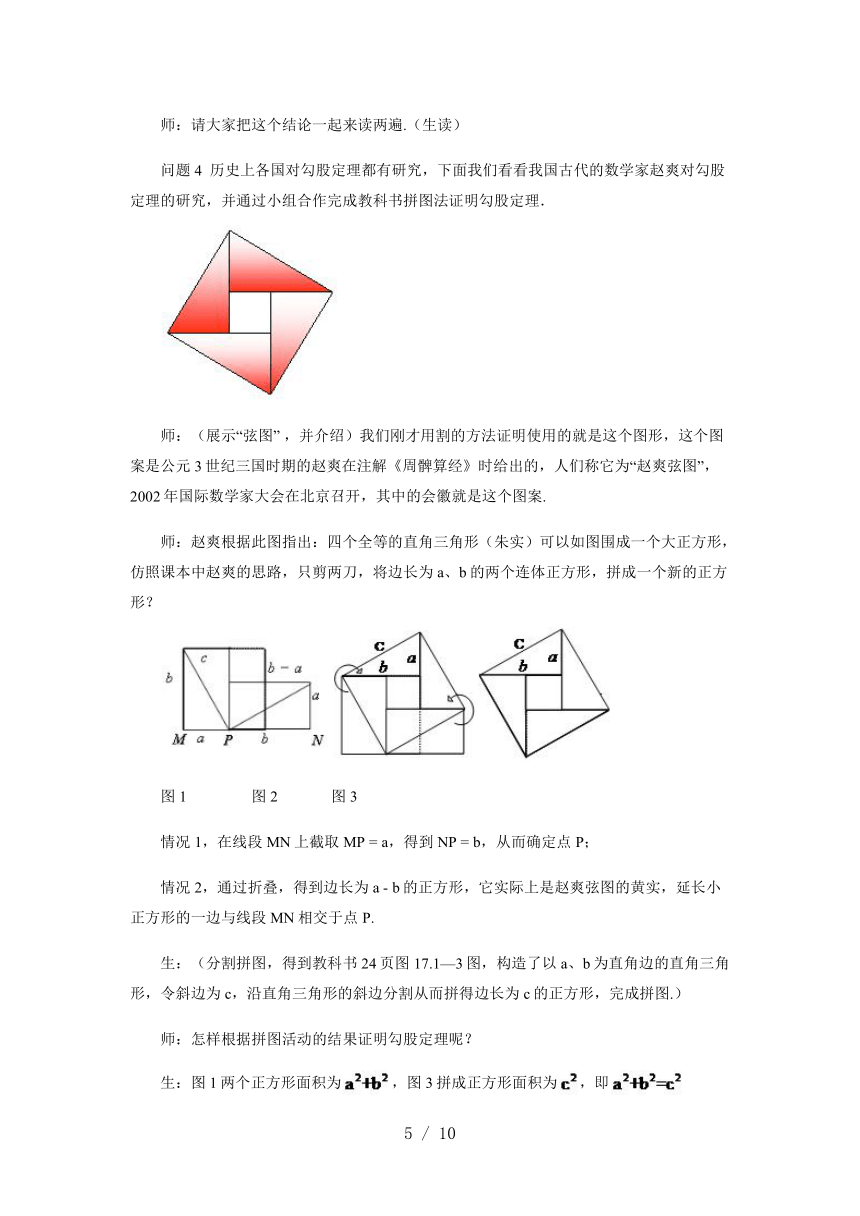
问题4??历史上各国对勾股定理都有研究,下面我们看看我国古代的数学家赵爽对勾股定理的研究,并通过小组合作完成教科书拼图法证明勾股定理.
师:(展示“弦图”?,并介绍)我们刚才用割的方法证明使用的就是这个图形,这个图案是公元3世纪三国时期的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,2002年国际数学家大会在北京召开,其中的会徽就是这个图案.
师:赵爽根据此图指出:四个全等的直角三角形(朱实)可以如图围成一个大正方形,仿照课本中赵爽的思路,只剪两刀,将边长为a、b的两个连体正方形,拼成一个新的正方形?
图1?????????????????图2??????????????图3
情况1,在线段MN上截取MP?=?a,得到NP?=?b,从而确定点P;
情况2,通过折叠,得到边长为a?-?b的正方形,它实际上是赵爽弦图的黄实,延长小正方形的一边与线段MN相交于点P.?
生:(分割拼图,得到教科书24页图17.1—3图,构造了以a、b为直角边的直角三角形,令斜边为c,沿直角三角形的斜边分割从而拼得边长为c的正方形,完成拼图.)
师:怎样根据拼图活动的结果证明勾股定理呢?
生:图1两个正方形面积为,图3拼成正方形面积为,即
师:勾股定理的证明方法据说有400多种,有兴趣的同学可以搜集研究一下.
(课件/板书)
勾股定理
????如果直角三角形的两直角边分别为a、b,斜边为c,那么.
问题5???画一个直角三角形,,它的两直角边分别是AC=3cm,BC=4cm,量一量它的斜边是多少厘M?算一算,你量的结果对吗?
师:画一个直角三角形,,它的两直角边分别是AC=3cm,BC=4cm,量一量它的斜边是多少厘M?算一算,你量的结果对吗?(学生动手操作、计算,教师个别指导)
生:结果一样.
(课件/板书)
在Rt△ACB中,∠C=90°,
AC=3cm,?BC=4cm.
由勾股定理得:
AB2=AC2+BC2,
=32+42=25
∴AB=5cm
师:我们可以利用勾股定理解决直角三角形中已知两边求第三边的问题.这是勾股定理最重要的应用.
3?典例剖析
例1??如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是多少?
解:∵BD平分∠ABC,
∴点D到AB的距离等于点D到BC距离,
过D作DM⊥BC,则DM=DA,
例2???如图,是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两孔中心A和B的距离.
解:在Rt△ACB中,∠C=90°,
AC=120-60=60(mm)
BC=140-60=80(mm).
由勾股定理得:AB2=AC2+BC2,
∴AB=100(mm)
答:两孔中心A和B的距离为100?mm.
4?巩固提升
1.一个直角三角形的两直角边长分别为3和4,下列说法正确的是(C)
A.斜边长为25B.三角形的周长为25
C.斜边长为5??D.三角形的面积为20
2.一架25?dm的梯子,斜靠在一竖直的墙上,这时梯足距墙底7?dm,如果梯子的顶端沿墙下滑4?dm,那么梯足将滑(D)
A.9?dm??B.15?dm
C.5?dm??D.8?dm
3.在Rt△ABC中,斜边AB=2,则BC2+CA2=___4___.
4.在△ABC中,∠C=90°,a=9,b=12,则c=___15___.
5.若直角三角形两直角边之比为3∶4,斜边长为20,则两条直角边分别为__12__,__16___,它的面积为__96__.
6.如图,一根旗杆在离地面9?m处折断,旗杆顶部落在离旗杆底部12?m处.旗杆在折断之前有多高?
解:依题意得AC⊥BC,
在Rt△ABC中,由勾股定理得
AC2+BC2=AB2,
∴AB2=92+122=225.?
∴AB=15,AB+AC=9+15=24,
∴旗杆在折断之前高24?m.
??课堂小结
(一)学生总结
这节课学习了什么?你有什么收获?(小组说--组内总结--组间交流)
1.勾股定理证明:
⑴割补法
⑵拼接法
2.勾股定理:直角三角形两直角边的平方和等于斜边的平方.
3.?勾股定理的应用:已知两边求第三边
(二)教师总结
今天,我们通过自己的努力,学会了这么多知识,老师真为你们骄傲!同时我们还发现很多数学知识都是相互联系、相互贯通的。我们在学习时要做到举一反三,运用旧知识来学到更多的新知识。
??板书
/
1.??教案目标
1.1 知识与技能:
通过观察、计算、猜想直角三角形两条直角边的平方和等于斜边的平方的结论.
1.2 过程与方法:
1.在充分观察、归纳、猜想、探索直角三角形两条直角边的平方和等于斜边的平方的过程中,发展合情推理能力,体会数形结合的思想.
2.在探索上述结论的过程中,发展归纳、概括和有条理地表达活动的过程和结论.
1.3情感态度与价值观:
1.树立积极参与、合作交流的意识.
2.在探索勾股定理的过程中,体验获得结论的快乐,锻炼克服困难的勇气.
2.??教案重点/难点
2.1 教案重点:
探索直角三角形两条直角边的平方和等于斜边的平方的结论,从而发现勾股定理.
2.2 教案难点:
以直角三角形的边为边的正方形面积的计算.
3.??教案用具
4.??标签
??教案过程
1?谈话引入
我们知道,研究三角形从它的元素入手,也就是三角形的三条边和三个角。对于等腰三角形和等边三角形的边,除满足三边关系定理外,它们还分别存在着两边相等和三边相等的特殊关系。那么对于直角三角形的边,除满足三边关系定理外,它们之间也存在着特殊的关系,这就是我们这一节要研究的问题:勾股定理.
推进新课
(板书课题:勾股定理)
2?新知探究
问题1???相传2500多年前,古希腊著名的哲学家、数学家、天文学家,毕达哥拉斯有一次在朋友家作客,发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.观察下面图中的地面,看看你能发现什么?三个正方形A,B,C的面积有什么关系?
师:同学们,我们也来是否也和大哲学家有同样的发现呢?观察三个正方形之间的面积的关系.
生:两个小正方形的面积之和等于大正方形的面积.
师:为什么?
生:……(通过直接数等腰直角三角形的个数,或者用割补的方法将小正方形A,B中的等腰直角三角形补成一个大正方形,得出结论:小正方形A,B的面积之和等于大正方形C的面积.)
师:这里每个正方形的面积等于其边长的平方.于是这三个正方形的边长构成的等腰直角三角形三条边长之间有怎样的特殊关系?
生:等腰直角三角形两条直角边的平方和等于斜边的平方.
师:等腰直角三角形是特殊的直角三角形,接下来探究问题2.
问题2 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A,B,C的面积是否也有类似的关系?
师:如图,?以直角三角形的三边为边长作三个正方形A、B、C,并计算他们的面积.(学生动手计算,教师巡视指导)
师:谁来说一说?
生:图1:正方形A、B、C的面积分别为16、9、25;图2:正方形A、B、C的面积分别为4、9、13.
师:正方形C的面积你是如何计算的?
生:……(通过割、补两种方法求出其面积)
(课件/板书)
图1???SC
图2??SC
师:这里注意正方形的面积又转化为边长的平方,于是正方形A,B,C所围成的直角三角形三条边之间有怎样的关系?
生:直角三角形两条直角边的平方和等于斜边的平方.
师:接下来我们来看问题3.
问题3??以上直角三角形的边长都是具体的数值,一般情况下,如果直角三角形的两直角边分别为a,b,斜边长为c,我们的猜想仍然成立吗?
师:这个结论仍然成立,中国人称它为“勾股定理”,外国人称它为“毕达哥拉斯定理”.
师:我国是最早发现勾股定理的国家之一,据《周髀算经》记载:公元前1100年人们已经知道“勾广三,股修四,径隅五”.?把直角三角形中较短的直角边称为勾,较长的称为股,斜边称为弦.?将此定理命名为勾股定理.
师:他有非常多证明方法,这里我们依然可以利用刚才的割补法.
(课件/板书)
“割”的方法:,于是.
“补”的方法:,于是.
(课件/板书)
勾股定理
直角三角形两直角边的平方和等于斜边的平方.?
师:请大家把这个结论一起来读两遍.(生读)
问题4??历史上各国对勾股定理都有研究,下面我们看看我国古代的数学家赵爽对勾股定理的研究,并通过小组合作完成教科书拼图法证明勾股定理.
师:(展示“弦图”?,并介绍)我们刚才用割的方法证明使用的就是这个图形,这个图案是公元3世纪三国时期的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,2002年国际数学家大会在北京召开,其中的会徽就是这个图案.
师:赵爽根据此图指出:四个全等的直角三角形(朱实)可以如图围成一个大正方形,仿照课本中赵爽的思路,只剪两刀,将边长为a、b的两个连体正方形,拼成一个新的正方形?
图1?????????????????图2??????????????图3
情况1,在线段MN上截取MP?=?a,得到NP?=?b,从而确定点P;
情况2,通过折叠,得到边长为a?-?b的正方形,它实际上是赵爽弦图的黄实,延长小正方形的一边与线段MN相交于点P.?
生:(分割拼图,得到教科书24页图17.1—3图,构造了以a、b为直角边的直角三角形,令斜边为c,沿直角三角形的斜边分割从而拼得边长为c的正方形,完成拼图.)
师:怎样根据拼图活动的结果证明勾股定理呢?
生:图1两个正方形面积为,图3拼成正方形面积为,即
师:勾股定理的证明方法据说有400多种,有兴趣的同学可以搜集研究一下.
(课件/板书)
勾股定理
????如果直角三角形的两直角边分别为a、b,斜边为c,那么.
问题5???画一个直角三角形,,它的两直角边分别是AC=3cm,BC=4cm,量一量它的斜边是多少厘M?算一算,你量的结果对吗?
师:画一个直角三角形,,它的两直角边分别是AC=3cm,BC=4cm,量一量它的斜边是多少厘M?算一算,你量的结果对吗?(学生动手操作、计算,教师个别指导)
生:结果一样.
(课件/板书)
在Rt△ACB中,∠C=90°,
AC=3cm,?BC=4cm.
由勾股定理得:
AB2=AC2+BC2,
=32+42=25
∴AB=5cm
师:我们可以利用勾股定理解决直角三角形中已知两边求第三边的问题.这是勾股定理最重要的应用.
3?典例剖析
例1??如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是多少?
解:∵BD平分∠ABC,
∴点D到AB的距离等于点D到BC距离,
过D作DM⊥BC,则DM=DA,
例2???如图,是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两孔中心A和B的距离.
解:在Rt△ACB中,∠C=90°,
AC=120-60=60(mm)
BC=140-60=80(mm).
由勾股定理得:AB2=AC2+BC2,
∴AB=100(mm)
答:两孔中心A和B的距离为100?mm.
4?巩固提升
1.一个直角三角形的两直角边长分别为3和4,下列说法正确的是(C)
A.斜边长为25B.三角形的周长为25
C.斜边长为5??D.三角形的面积为20
2.一架25?dm的梯子,斜靠在一竖直的墙上,这时梯足距墙底7?dm,如果梯子的顶端沿墙下滑4?dm,那么梯足将滑(D)
A.9?dm??B.15?dm
C.5?dm??D.8?dm
3.在Rt△ABC中,斜边AB=2,则BC2+CA2=___4___.
4.在△ABC中,∠C=90°,a=9,b=12,则c=___15___.
5.若直角三角形两直角边之比为3∶4,斜边长为20,则两条直角边分别为__12__,__16___,它的面积为__96__.
6.如图,一根旗杆在离地面9?m处折断,旗杆顶部落在离旗杆底部12?m处.旗杆在折断之前有多高?
解:依题意得AC⊥BC,
在Rt△ABC中,由勾股定理得
AC2+BC2=AB2,
∴AB2=92+122=225.?
∴AB=15,AB+AC=9+15=24,
∴旗杆在折断之前高24?m.
??课堂小结
(一)学生总结
这节课学习了什么?你有什么收获?(小组说--组内总结--组间交流)
1.勾股定理证明:
⑴割补法
⑵拼接法
2.勾股定理:直角三角形两直角边的平方和等于斜边的平方.
3.?勾股定理的应用:已知两边求第三边
(二)教师总结
今天,我们通过自己的努力,学会了这么多知识,老师真为你们骄傲!同时我们还发现很多数学知识都是相互联系、相互贯通的。我们在学习时要做到举一反三,运用旧知识来学到更多的新知识。
??板书
/
