人教版数学必修1 2.1 指数函数单元复习:22张PPT
文档属性
| 名称 | 人教版数学必修1 2.1 指数函数单元复习:22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 23:04:41 | ||
图片预览








文档简介
课件22张PPT。指数函数单元复习现有一张1mm的厚纸板,不断地将其对折,每次折叠后的厚度如何表示?将其折叠50次后,对其厚度描述准确的是 第一次对折后:1×2=2,250≈5.63×1013(mm)=5.63*1010(m)第二次对折后:2×2=22,第三次对折后:22×2=23,……第n次对折后: 2n-1×2=2n (1)一张课桌的高度
(2)一座平房的高度
(3)栖霞一中教学楼的高度
(4)超过地球和月球的之间的距离(地球和月球之
间的平均距离 约3.84×108m) 负数没有偶次方根式子____叫做根式,___叫做根指数,
___叫被开方数。1、基本概念:没有意义——1、基本概念:(3)幂的运算性质(4)指数函数:一般地,函数____________________叫做指数函数,
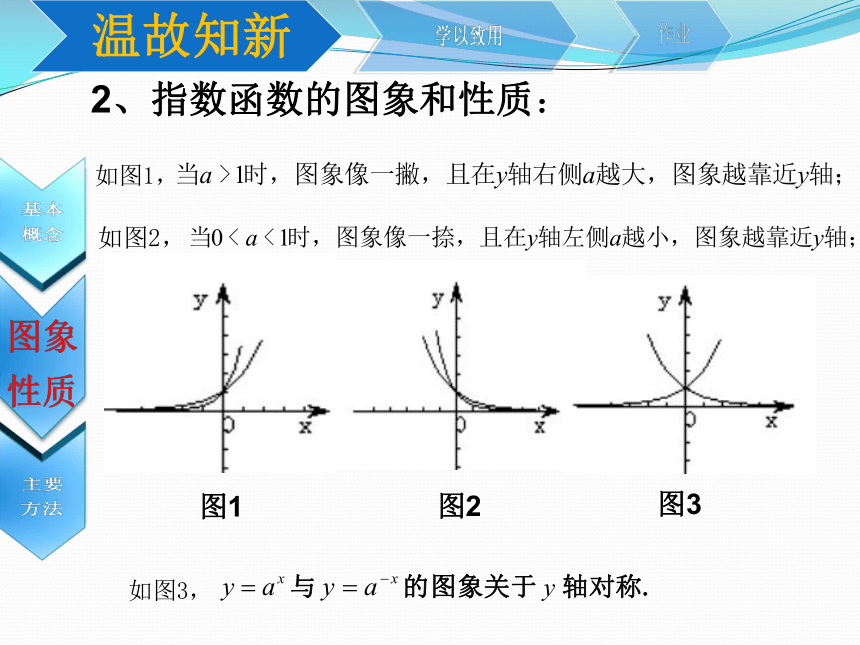
其中x是自变量.1、基本概念:2、指数函数的图象和性质:2、指数函数的图象和性质:3、主要方法: (1)指数方程,指数不等式:常要转化为同底数的形式,再利用指数函数的单调性求解; (2)确定与指数有关的函数的单调性时,常要注意针对底数进行讨论;(3)要注意运用数形结合思想解决问题.(一)指数与指数幂的运算部分[解题思路]根式的形式通常写成分数指数幂后进行运算.解:解:解:∴选C.牛刀小试:A(一)指数与指数幂的运算部分(二)指数函数与性质部分例2.函数y=(a2-3a+3)ax是指数函数,则有( )
A.a=1或a=2 B.a=1 C.a =2 D.a >0且a ≠11)定义:C练习:指数函数y=f(x)的图象经过点(2,4),那么f(2)·f(4)=___642)定义域与值域:A3)图像的考察(二)指数函数与性质部分B3)图像的考察(二)指数函数与性质部分4)单调性的应用类型一:比较大小(二)指数函数与性质部分4)单调性的应用类型二:解不等式(二)指数函数与性质部分5)过定点问题(二)指数函数与性质部分D6)底数与图像形状的关系:(二)指数函数与性质部分(三)本节小结1)指数幂运算要化成分数指数幂的形式,利用运算法则
运算,多重根式要从內至外依次展开;2)有关指数函数的问题要结合图像作出思考,即要熟练
应用数形结合的数学思想;3)确定与指数有关的函数的单调性时,常要注意针对底数
进行讨论.作业(必做题目):作业(必做题目):作业(必做题目):作业(选做题目):
(2)一座平房的高度
(3)栖霞一中教学楼的高度
(4)超过地球和月球的之间的距离(地球和月球之
间的平均距离 约3.84×108m) 负数没有偶次方根式子____叫做根式,___叫做根指数,
___叫被开方数。1、基本概念:没有意义——1、基本概念:(3)幂的运算性质(4)指数函数:一般地,函数____________________叫做指数函数,
其中x是自变量.1、基本概念:2、指数函数的图象和性质:2、指数函数的图象和性质:3、主要方法: (1)指数方程,指数不等式:常要转化为同底数的形式,再利用指数函数的单调性求解; (2)确定与指数有关的函数的单调性时,常要注意针对底数进行讨论;(3)要注意运用数形结合思想解决问题.(一)指数与指数幂的运算部分[解题思路]根式的形式通常写成分数指数幂后进行运算.解:解:解:∴选C.牛刀小试:A(一)指数与指数幂的运算部分(二)指数函数与性质部分例2.函数y=(a2-3a+3)ax是指数函数,则有( )
A.a=1或a=2 B.a=1 C.a =2 D.a >0且a ≠11)定义:C练习:指数函数y=f(x)的图象经过点(2,4),那么f(2)·f(4)=___642)定义域与值域:A3)图像的考察(二)指数函数与性质部分B3)图像的考察(二)指数函数与性质部分4)单调性的应用类型一:比较大小(二)指数函数与性质部分4)单调性的应用类型二:解不等式(二)指数函数与性质部分5)过定点问题(二)指数函数与性质部分D6)底数与图像形状的关系:(二)指数函数与性质部分(三)本节小结1)指数幂运算要化成分数指数幂的形式,利用运算法则
运算,多重根式要从內至外依次展开;2)有关指数函数的问题要结合图像作出思考,即要熟练
应用数形结合的数学思想;3)确定与指数有关的函数的单调性时,常要注意针对底数
进行讨论.作业(必做题目):作业(必做题目):作业(必做题目):作业(选做题目):
