人教版数学必修1 3.2.2 函数模型的应用实例(第一课时):22张PPT
文档属性
| 名称 | 人教版数学必修1 3.2.2 函数模型的应用实例(第一课时):22张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 381.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 10:07:25 | ||
图片预览



文档简介
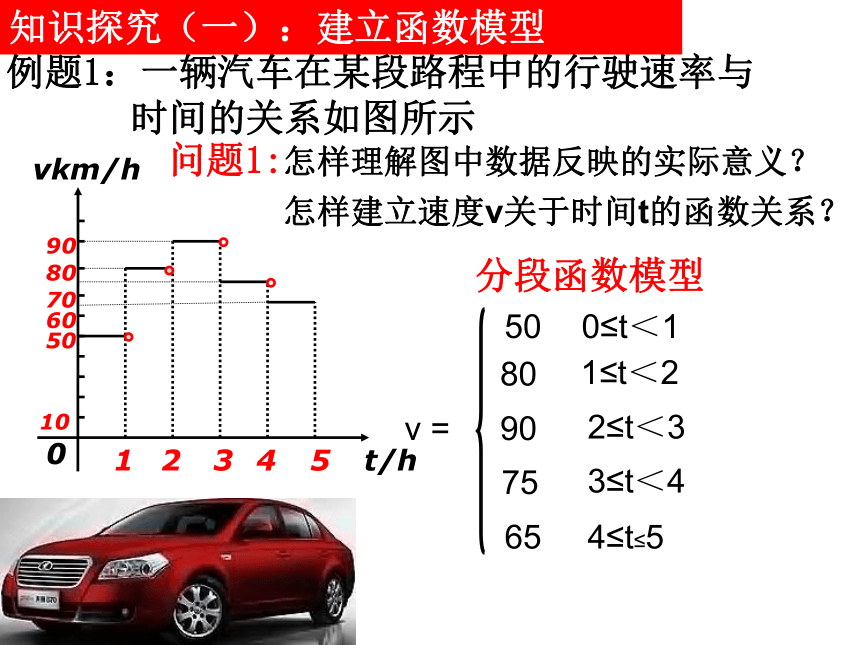
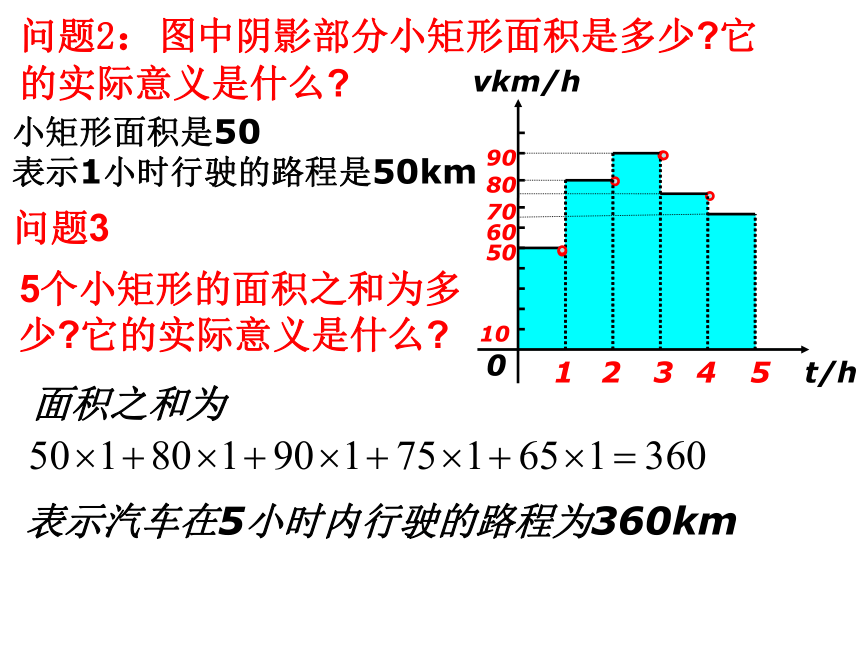
课件22张PPT。第一课时函数模型的应用实例一、复习巩固一次函数二次函数指数函数对数函数幂函数正比例函数反比例函数 一次函数、二次函数、指数函数、对数函数以及幂函数等函数模型,它们都与现实世界有着紧密的联系,广泛的应用。我们如何利用这些函数模型来解决实际问题? 问题1:怎样理解图中数据反映的实际意义? 例题1:一辆汽车在某段路程中的行驶速率与 时间的关系如图所示 知识探究(一):建立函数模型分段函数模型怎样建立速度v关于时间t的函数关系?问题2:图中阴影部分小矩形面积是多少?它的实际意义是什么?面积之和为表示汽车在5小时内行驶的路程为360km5个小矩形的面积之和为多少?它的实际意义是什么?小矩形面积是50
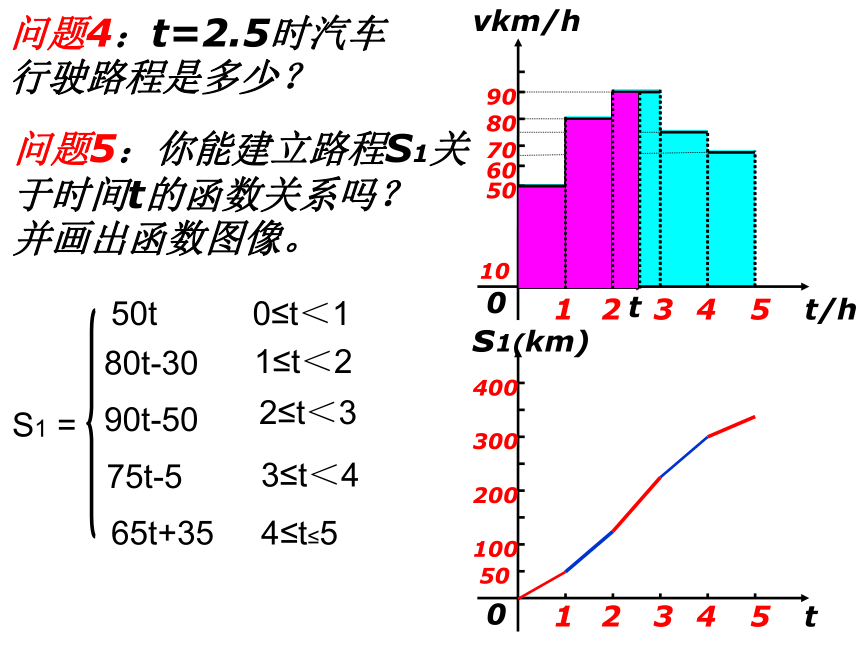
表示1小时行驶的路程是50km问题3问题4:t=2.5时汽车行驶路程是多少?问题5:你能建立路程S1关于时间t的函数关系吗?
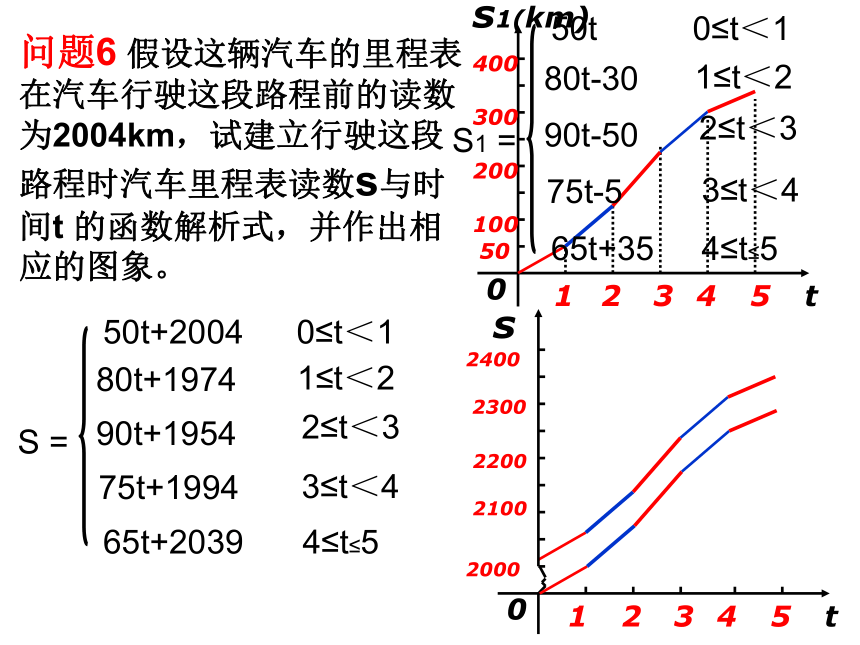
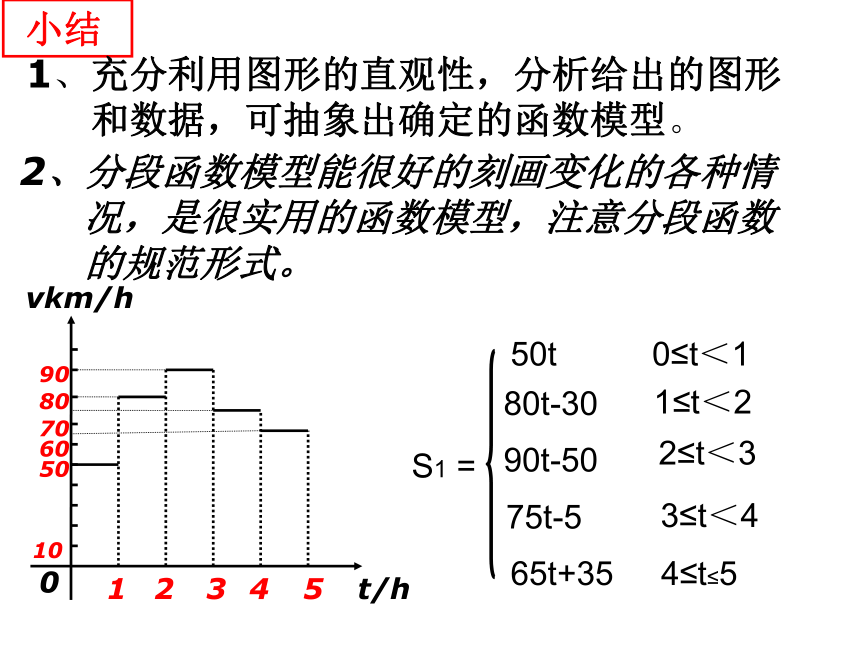
并画出函数图像。t问题6 假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,并作出相应的图象。 小结1、充分利用图形的直观性,分析给出的图形
和数据,可抽象出确定的函数模型。2、分段函数模型能很好的刻画变化的各种情
况,是很实用的函数模型,注意分段函数
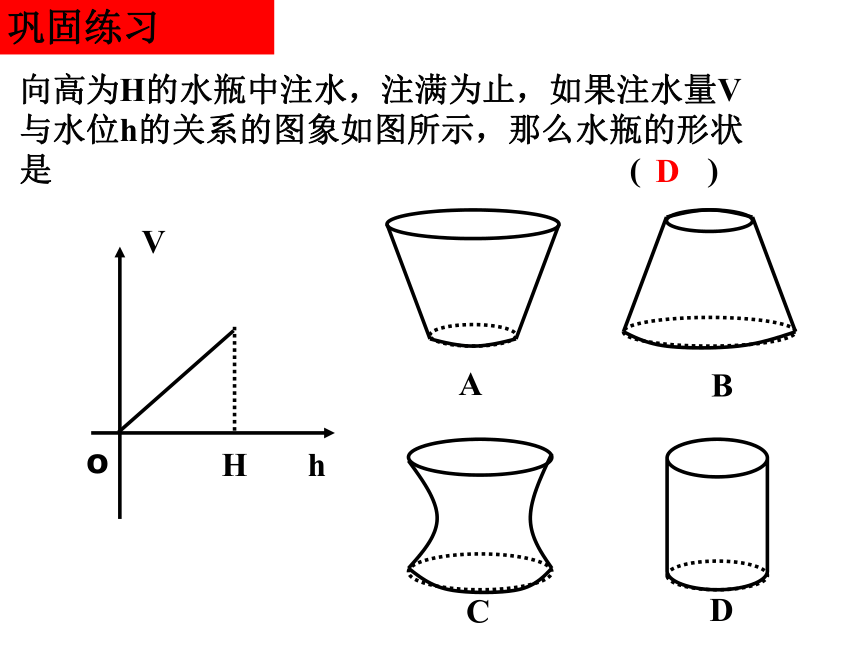
的规范形式。向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCD巩固练习DABCA巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCB巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCC巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
例2 人口问题是当年世界各国普遍关注的问题。认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:
知识探究(二):函数模型的应用马尔萨斯人口增长模型:下表是1950~1959年我国的人口数据资料:其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率。问题1如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型。解:设1951~1959年期间我国人口的增长率
分别是r1,r2,...,r9.y0=55196,问题2:怎样检验该模型与我国实际人口数据是否
相符? 由图可以看出,所得模型与1951~1959的实际人口数据基本吻合。问题3:据此人口增长模型,大约在哪一年
我国的人口达到13亿? 解:将 y=130000代入t≈38.76实际上2005年1月6日
我国人口达到13亿。按表中的增长趋势,大约在1950年后的39年(1989年)
我国人口达到13亿。知识拓展:
据此人口增长模型,1650年世界人口为5亿,当时人口的年增长率为0.3%,经计算大约1881年(231年后)世界人口达到10亿。
1970年世界人口为36亿,当时人口的年增长率为
2.1%,经计算大约2003年(33年后)世界人口达到72亿。
实际上1850年以前世界人口就超过了10亿,而2003年世界人口还没达到72亿。特别提醒:此模型不太适宜估计时间跨度非常大的人口增长情况。因此用已知的函数模型刻画实际问题的时候,由于实际问题的条件与得出已知模型的条件有所不同,通过模型得出的结果往往会与实际问题存在一定的误差。往往需要对模型进行修正。2、解函数应用题的一般步骤:(1)审题.读懂题目认真审题(2)建模.建立数学模型(3)求解.选择合适的数学方法,设计合理的运算途
径,求出问题的答案。(4)作答.将计算结果转移到实际问题中作答。实际问题数学模型数学模型的解1、已知函数类型时,可利用待定系数法求函数
解析式。知识总结某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价P与上市时间t的关系用下图的一条折线表示,写出市场售价与时间的函数关系式P=f(t)巩固提升:函数模型的应用巩固提升:函数模型的应用课堂小结1、解函数应用题的一般步骤:注意:
(1)分段函数的规范形式。
(2)写出函数解析式后,要标清定义域使实际
问题有意义。
(3)运用数形结合,转化与化归等思想方法解
决问题。2、解有关函数的应用题,要充分挖掘题目的隐含
条件,充分利用函数图形的直观性,考虑选择
哪一种函数作为模型,然后建立其解析式.已知
函数类型时,一般利用待定系数法求解析式。
表示1小时行驶的路程是50km问题3问题4:t=2.5时汽车行驶路程是多少?问题5:你能建立路程S1关于时间t的函数关系吗?
并画出函数图像。t问题6 假设这辆汽车的里程表在汽车行驶这段路程前的读数为2004km,试建立行驶这段路程时汽车里程表读数s与时间t 的函数解析式,并作出相应的图象。 小结1、充分利用图形的直观性,分析给出的图形
和数据,可抽象出确定的函数模型。2、分段函数模型能很好的刻画变化的各种情
况,是很实用的函数模型,注意分段函数
的规范形式。向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCD巩固练习DABCA巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCB巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
ABCC巩固练习D向高为H的水瓶中注水,注满为止,如果注水量V
与水位h的关系的图象如图所示,那么水瓶的形状
是 ( )
例2 人口问题是当年世界各国普遍关注的问题。认识人口数量的变化规律,可以为有效控制人口增长提供依据。早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型:
知识探究(二):函数模型的应用马尔萨斯人口增长模型:下表是1950~1959年我国的人口数据资料:其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率。问题1如果以各年人口增长率的平均值作为我国这一时期的人口增长率(精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型。解:设1951~1959年期间我国人口的增长率
分别是r1,r2,...,r9.y0=55196,问题2:怎样检验该模型与我国实际人口数据是否
相符? 由图可以看出,所得模型与1951~1959的实际人口数据基本吻合。问题3:据此人口增长模型,大约在哪一年
我国的人口达到13亿? 解:将 y=130000代入t≈38.76实际上2005年1月6日
我国人口达到13亿。按表中的增长趋势,大约在1950年后的39年(1989年)
我国人口达到13亿。知识拓展:
据此人口增长模型,1650年世界人口为5亿,当时人口的年增长率为0.3%,经计算大约1881年(231年后)世界人口达到10亿。
1970年世界人口为36亿,当时人口的年增长率为
2.1%,经计算大约2003年(33年后)世界人口达到72亿。
实际上1850年以前世界人口就超过了10亿,而2003年世界人口还没达到72亿。特别提醒:此模型不太适宜估计时间跨度非常大的人口增长情况。因此用已知的函数模型刻画实际问题的时候,由于实际问题的条件与得出已知模型的条件有所不同,通过模型得出的结果往往会与实际问题存在一定的误差。往往需要对模型进行修正。2、解函数应用题的一般步骤:(1)审题.读懂题目认真审题(2)建模.建立数学模型(3)求解.选择合适的数学方法,设计合理的运算途
径,求出问题的答案。(4)作答.将计算结果转移到实际问题中作答。实际问题数学模型数学模型的解1、已知函数类型时,可利用待定系数法求函数
解析式。知识总结某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价P与上市时间t的关系用下图的一条折线表示,写出市场售价与时间的函数关系式P=f(t)巩固提升:函数模型的应用巩固提升:函数模型的应用课堂小结1、解函数应用题的一般步骤:注意:
(1)分段函数的规范形式。
(2)写出函数解析式后,要标清定义域使实际
问题有意义。
(3)运用数形结合,转化与化归等思想方法解
决问题。2、解有关函数的应用题,要充分挖掘题目的隐含
条件,充分利用函数图形的直观性,考虑选择
哪一种函数作为模型,然后建立其解析式.已知
函数类型时,一般利用待定系数法求解析式。
