人教版数学必修1 2.2.2 对数函数及其性质:20张PPT
文档属性
| 名称 | 人教版数学必修1 2.2.2 对数函数及其性质:20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 889.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 00:00:00 | ||
图片预览





文档简介
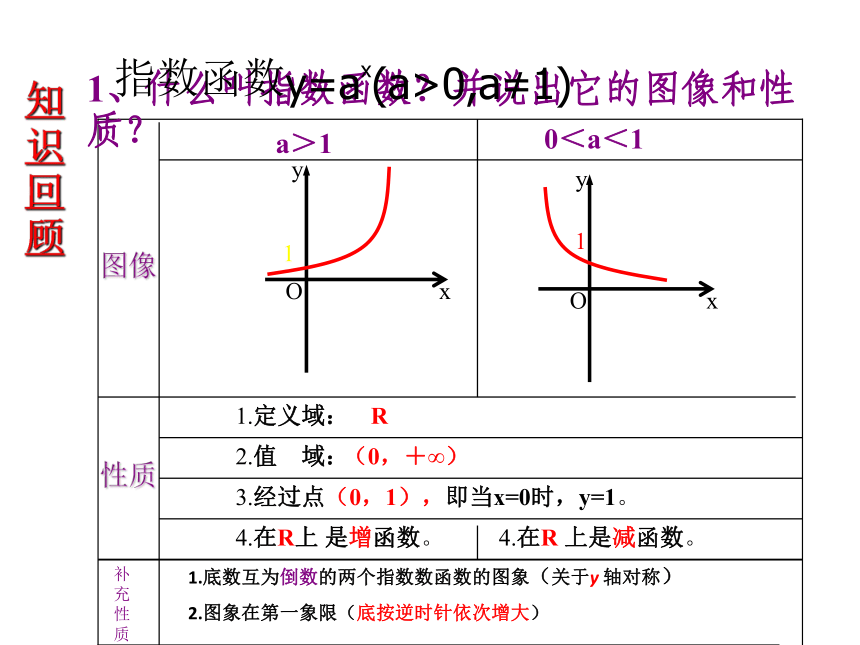
课件20张PPT。知识回顾1、什么叫指数函数?并说出它的图像和性质?1.定义域:R3.经过点(0,1),即当x=0时,y=1。4.在R上 是增函数。 4.在R 上是减函数。
11(0,+∞)2.值 域:1.底数互为倒数的两个指数数函数的图象(关于y 轴对称)
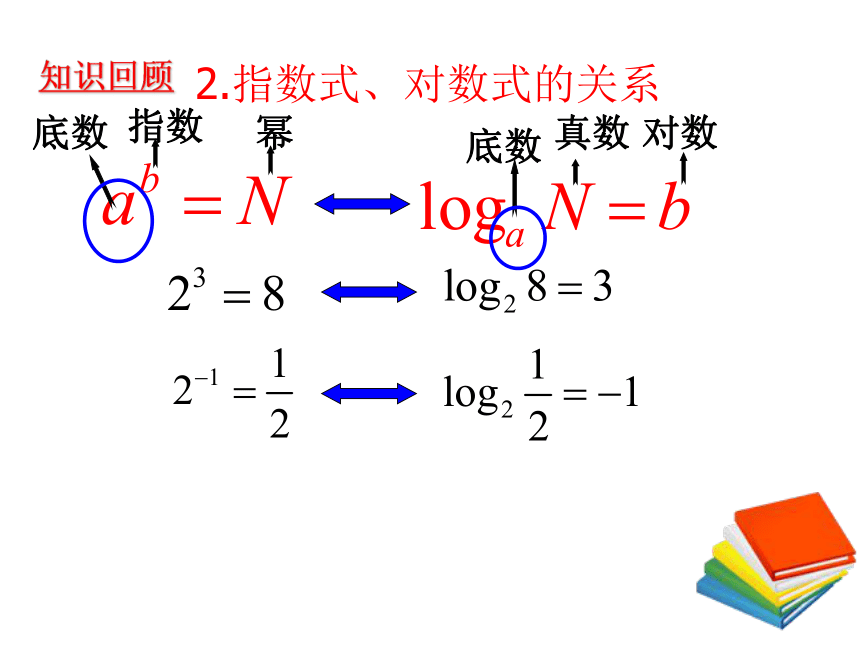
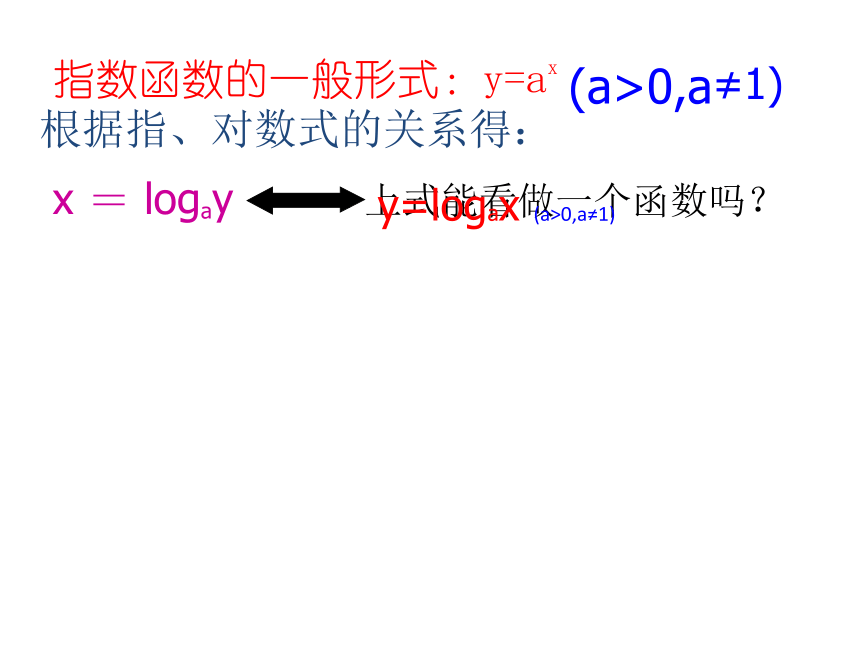
2.图象在第一象限(底按逆时针依次增大)指数函数y=ax(a>0,a≠1)补充性质底数指数幂底数真数对数2.指数式、对数式的关系知识回顾指数函数的一般形式:y=ax (a>0,a≠1)根据指、对数式的关系得:x = logay上式能看做一个函数吗?y=logax (a>0,a≠1)根据对数函数和指数函数y=ax 的关系,
思考对数函数的定义域是什么?1.定义域和值域对调
2.图像关于直线y=x对称指数函数与对数函数之间的关系(x,y)(y,x)定义域是(0,+∞) 值域是R 思考;对数函数的图像?怎么画?(1,0)(1,0)00据对称性由指数函数的图象可得对数函数的图象(0,1)(0,1)图像特征:1图像整体位于y轴右侧
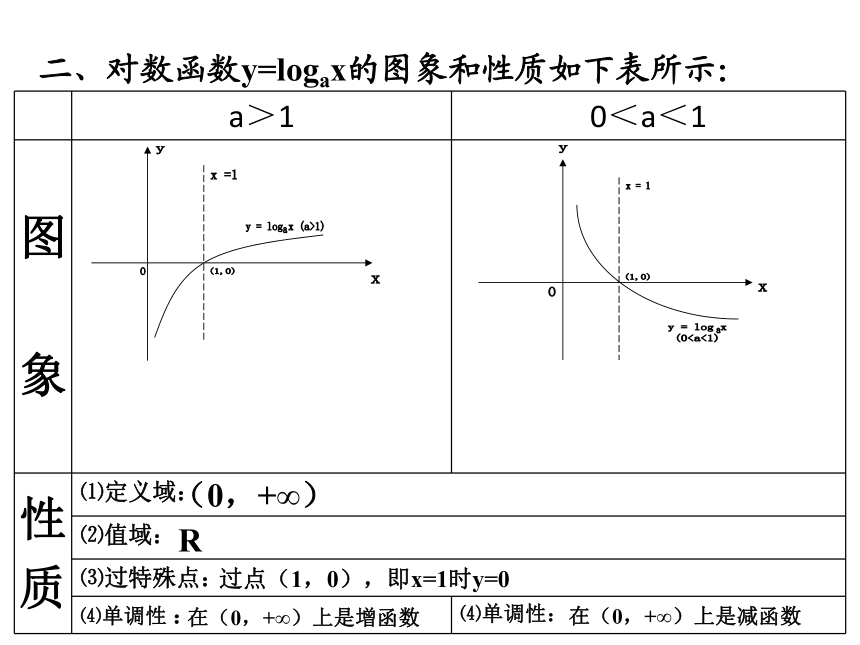
2、无限接近y轴但不相交 3、恒过点(1,0) 二、对数函数y=logax的图象和性质如下表所示:?
(0,+∞)R过点(1,0),即x=1时y=0在(0,+∞)上是增函数在(0,+∞)上是减函数在同一坐标系下画出 在第一象限按逆时针方向底数减小。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy题型一:求函数的定义域:
①y=logax2 ②y=loga(4-x) ③y=loga(9-x2)分析:此题主要利用对数函数y=logax的定义域为(0,+∞)求解。①因为x2 >0,即x≠0,
所以函数y=logax2 的定义域是{x│x≠0} ②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4} ③因为9-x2>0,即-3 所以函数y=loga(9-x2)的定义域是{x│-3解;要使函数有意义需满足所以小 结求函数定义域的方法:1. 分数的分母不能为零;3. 偶次方根的被开方数大于等于零;4. 对数的真数必须大于零;5. 指数、对数的底数必须大于零且不等于1.2. 零的指数不能为零和负数;例2、比较下列各数的大小. (1) log23.4 , log28.5 ;(2) log0.31.8 , log0.32.7; (3) loga5.1, loga5.9 (a>0,a≠1)
(4)log 67 , log 7 6 ;
(5)log 32, log 2 0.8 .类型2:利用性质比较大小应用例2:比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7log23.4log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∵3.4<8.5∴ log23.4< log28.5 ∴ log23.4< log28.5 ∴ y=log2x在(0,+∞)
上是增函数; 注意:若底数不确定,那就要对底数进行分类讨论
即0 1
(3) loga5.1与 loga5.9(a>o,且a≠1)解: 若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
若0 ∵5.1<5.9
∴ loga5.1 > loga5.9小 结比较大小的方法(1) 利用函数单调性(同底不同真)(3) 利用中间值(不同真不同底)(2) 利用图象(在第一象限按逆时针方向底数减小)比较(同真不同底)y10RR(0,+∞)(0,+∞)(0,1)(1,0)四.归纳小结思考题若函数求a的取值范围.
11(0,+∞)2.值 域:1.底数互为倒数的两个指数数函数的图象(关于y 轴对称)
2.图象在第一象限(底按逆时针依次增大)指数函数y=ax(a>0,a≠1)补充性质底数指数幂底数真数对数2.指数式、对数式的关系知识回顾指数函数的一般形式:y=ax (a>0,a≠1)根据指、对数式的关系得:x = logay上式能看做一个函数吗?y=logax (a>0,a≠1)根据对数函数和指数函数y=ax 的关系,
思考对数函数的定义域是什么?1.定义域和值域对调
2.图像关于直线y=x对称指数函数与对数函数之间的关系(x,y)(y,x)定义域是(0,+∞) 值域是R 思考;对数函数的图像?怎么画?(1,0)(1,0)00据对称性由指数函数的图象可得对数函数的图象(0,1)(0,1)图像特征:1图像整体位于y轴右侧
2、无限接近y轴但不相交 3、恒过点(1,0) 二、对数函数y=logax的图象和性质如下表所示:?
(0,+∞)R过点(1,0),即x=1时y=0在(0,+∞)上是增函数在(0,+∞)上是减函数在同一坐标系下画出 在第一象限按逆时针方向底数减小。 补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形10xy题型一:求函数的定义域:
①y=logax2 ②y=loga(4-x) ③y=loga(9-x2)分析:此题主要利用对数函数y=logax的定义域为(0,+∞)求解。①因为x2 >0,即x≠0,
所以函数y=logax2 的定义域是{x│x≠0} ②因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x│x<4} ③因为9-x2>0,即-3
(4)log 67 , log 7 6 ;
(5)log 32, log 2 0.8 .类型2:利用性质比较大小应用例2:比较下列各组中,两个值的大小:
(1) log23.4与 log28.5 (2) log 0.3 1.8与 log 0.3 2.7log23.4log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∵3.4<8.5∴ log23.4< log28.5 ∴ log23.4< log28.5 ∴ y=log2x在(0,+∞)
上是增函数; 注意:若底数不确定,那就要对底数进行分类讨论
即0
(3) loga5.1与 loga5.9(a>o,且a≠1)解: 若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
若0
∴ loga5.1 > loga5.9小 结比较大小的方法(1) 利用函数单调性(同底不同真)(3) 利用中间值(不同真不同底)(2) 利用图象(在第一象限按逆时针方向底数减小)比较(同真不同底)y10RR(0,+∞)(0,+∞)(0,1)(1,0)四.归纳小结思考题若函数求a的取值范围.
