京改版九年级数学上册 18.7《应用举例》 同步练习 (含答案)
文档属性
| 名称 | 京改版九年级数学上册 18.7《应用举例》 同步练习 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 09:39:46 | ||
图片预览



文档简介
北京课改版九年级数学上册
18.7《应用举例》
同步练习
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,铁道口栏杆的短臂长为1.2 m,长臂长为8 m,当短臂端点下降0.6 m时,(杆的粗细忽略不计)长臂端点升高( )
A.3 m B.4 m
C.5m D.6 m
2. 如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2 m,测得AB=1.6 m,BC=12.4 m,则建筑物CD的高是( )
A.9.3 m B.10.5 m
C.12.4 m D.14 m
3. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前,其中有首歌谣:今有竿不知其长,量得影长一丈五尺,立一标杆,长一尺五寸,影长五寸,问竿长几何?意即:如图,有一根竹竿不知道有多长,量出它在太阳下的影子长为一丈五尺,同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),则竹竿的长为( )
A.五丈 B.四丈五尺
C.一丈 D.五尺
4.学校门口的栏杆如图,将栏杆从水平位置BD绕点O旋转到AC的位置.已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4 m,AB=1.6 m,CO=1 m,则栏杆C端应下降的垂直距离CD为( )
A.0.2 m B.0.3 m
C.0.4 m D.0.5 m
5.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B.减小1.5米
C.增大3.5米 D.减小3.5米
6. 如图,小明在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离EB=20米,镜子与小明的距离ED=2米时,小明刚好从镜子中看到铁塔顶端A.已知小明的眼睛距地面的高度CD=1.6米,(根据光的反射原理,∠1=∠2)则铁塔AB的高度是( ).
A.16米 B.18米
C.12米 D.15米
7.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2 m,它的影子BC=1.6 m,木竿PQ的影子有一部分落在了墙上,PM=1.2 m,MN=0.8 m,则木竿PQ的长度为( )
A.2.3 m B.2.5 m
C.2.4 m D.2.1 m
8. 如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m.若两次日照的光线互相垂直,则树的高度为( )
A.3 m B. 5 m
C.4 m D.2 m
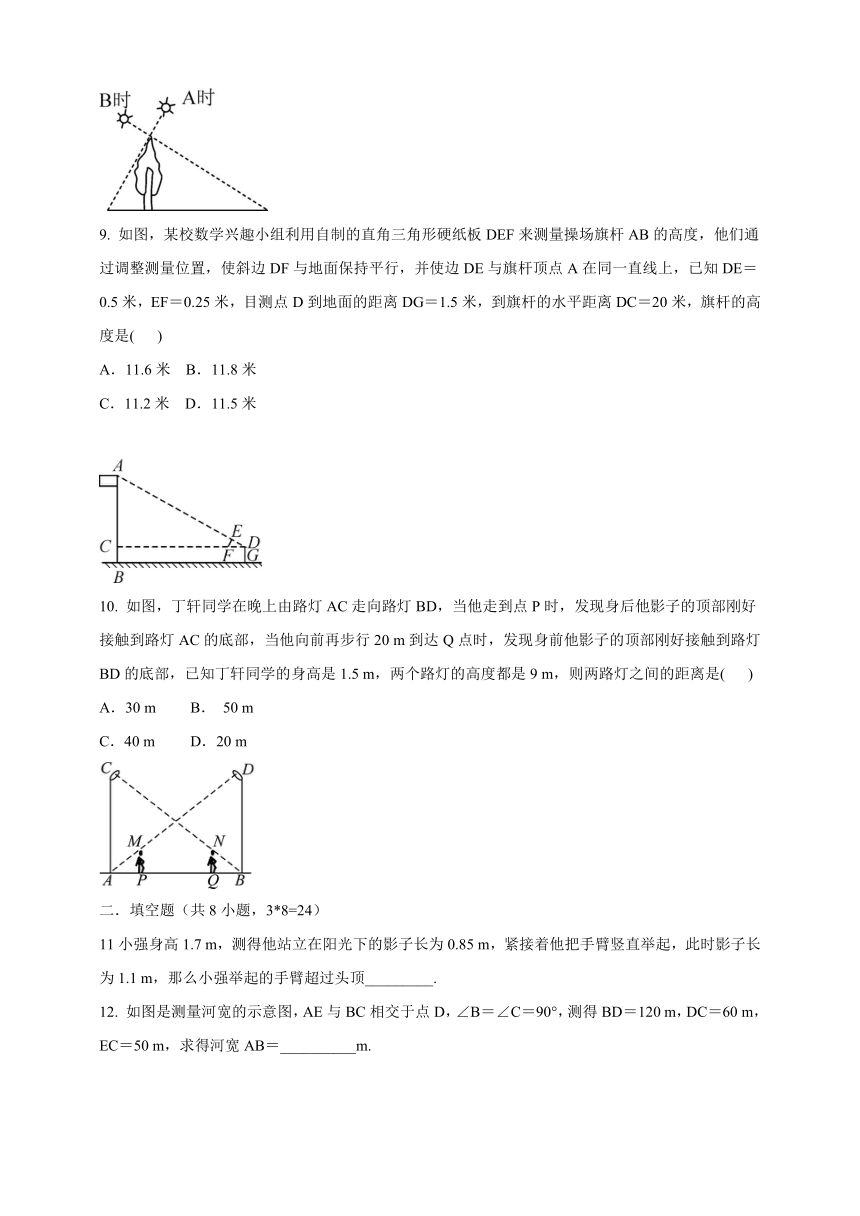
9. 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,旗杆的高度是( )
A.11.6米 B.11.8米
C.11.2米 D.11.5米
10. 如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是( )
A.30 m B. 50 m
C.40 m D.20 m
二.填空题(共8小题,3*8=24)
11小强身高1.7 m,测得他站立在阳光下的影子长为0.85 m,紧接着他把手臂竖直举起,此时影子长为1.1 m,那么小强举起的手臂超过头顶_________.
12. 如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120 m,DC=60 m,EC=50 m,求得河宽AB=__________m.
13. 九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为_______步.
14. 如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条边DF=50 cm,EF=30 cm,测得边DF离地面的高度AC=1.5 m,CD=20 m,则树高AB为__________.
15. 某同学想利用相似三角形的有关知识来求一座铁塔的高度.某一时刻,他先测量出铁塔落在地面上的影长为14 m,然后在同一时刻立一根高2 m的标杆,测得标杆影长为0.5 m,那么铁塔的高度为_______m.
16. 路边有一根电线杆AB和一块正方形广告牌,有一天,小明突然发现在太阳光照射下,电线杆顶端A的影子刚好落在正方形广告牌的上边中点G处,而正方形广告牌的影子刚好落在地面上的E点处(如图),已知BC=5 m,正方形广告牌的边长为2 m,DE=4 m,则此时电线杆的高度是_____m.
17.如图,身高为1.7 m的小明AB站在河的一岸,利用树的倒影去测量河对岸一棵树CD的高度,CD在水中的倒影为C′D,A,E,C′在一条线上,已知河BD的宽度为12 m,BE=3 m,则树CD的高为__________.
18.阳光通过窗口照射到室内,在地面上留下2.7 m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7 m,窗口高AB=1.8 m,则窗口底边离地面的高BC=_______m.
三.解答题(共7小题,46分)
19.(6分)某一时刻,身髙1.6 m的小明在阳光下的影长是0.4 m,同一时刻同一地点测得某旗杆的影长是5 m,则该旗杆的高度是多少?
20.(6分)如图,某班上体育课,当甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,求甲、乙两名同学相距多少米.
21.(6分)高明为了测量一大楼的高度,如图,在地面上放一平面镜,镜子与楼的距离AE=27 m,当他与镜子的距离是2.1 m时,刚好能从镜子中看到楼顶B,已知他的眼睛到地面的高度CD为1.6 m,结果他很快计算出大楼的高度AB,你知道是为什么吗?试加以说明.
22.(6分) 如图,矩形ABCD为台球桌面.AD=260 cm,AB=130 cm.球目前在点E的位置,AE=60 cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹,球刚好弹到点D的位置.
(1)求证:△BEF∽△CDF.
(2)求CF的长.
23.(6分) 如图,一油桶高AE为1 m,桶内有油,一根木棒AB的长为1.2 m,从桶盖的小口(A)处斜插入桶内,一端插到桶底,另一端与小口(A)齐平,抽出木棒,量得棒上未浸油部分AC的长为0.48 m.求桶内油面的高度DE.
24.(8分) 如图,某测量工作人员眼睛A与标杆顶端F、电视塔顶端E在同一直线上,已知此人眼睛距地面1.6米,标杆高为3.2米,且BC=1米,CD=5米,求电视塔的高ED.
25.(8分) 周末,小凯和同学带着皮尺,去测量杨大爷家露台遮阳篷的宽度.如图,由于无法直接测量,小凯便在楼前地面上选择了一条直线EF,通过在直线EF上选点观测,发现当他位于N点时,他的视线从M点通过露台D点正好落在遮阳篷A点处;当他位于N′点时,视线从M′点通过D点正好落在遮阳篷B点处,这样观测到的两个点A,B间的距离即为遮阳篷的宽.已知AB∥CD∥EF,点C在AG上,AG,DE,MN,M′N′均垂直于EF,MN=M′N′,露台的宽CD=GE.实际测得,GE=5米,EN=15.5米,NN′=6.2米.请根据以上信息,求出遮阳篷的宽AB是多少米?
参考答案:
1-5 BBBCD 6-10 AACDA
11.0.5 m
12. 100
13.
14.16.5 m
15. 56
16. 5
17. 5.1m
18. 4
19. 解:设该旗杆的高度为x m.
根据题意,得1.6∶0.4=x∶5,解得x=20.
即该旗杆的高度是20 m.
20. 解:设甲、乙两名同学相距x米.
∵△ADE∽△ACB,∴=,
即=,解得x=1.
答:甲、乙两名同学相距1米.
21. 解:∵反射角等于入射角,
∴∠BEA=∠DEC.
又∵AB⊥AC,DC⊥AC,
∴∠BAE=∠DCE=90°,
∴△ABE∽△CDE,∴=,
即=,解得AB=.
答:楼高AB为 m.
22. 证明:(1)∵∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF.
(2)由(1)知,△BEF∽△CDF.
∴=,即=,
解得CF=169.
即CF的长是169 cm.
23. 解:∵CD∥BE,∴△ACD∽△ABE,
∴=,即=,
∴=,解得DE=0.6.
答:桶内油面的高度DE为0.6 m.
24. 解:如图,作AG⊥ED交CF于点H,交DE于点G,
则△AFH∽△AEG,=,
FH=3.2-1.6=1.6,AH=BC=1,AG=6,
从而=,得EG=9.6,
ED=9.6+1.6=11.2(米),
即电视塔的高ED为11.2米
25. 解:延长MM′交DE于H,则HM=EN=15.5米,
CD=GE=5米,MM′=NN′=6.2米,
∵CD∥HM,∴∠ADC=∠DMH,
∴Rt△ACD∽Rt△DHM,
∴==,
∵AB∥MM′,∴△ABD∽△MM′D,
∴=,∴=,即=,解得AB=2米,
答:遮阳篷的宽AB是2米
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
