新教材人教B版数学必修第三册课件:7.2.1 三角函数的定义(51张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.2.1 三角函数的定义(51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览



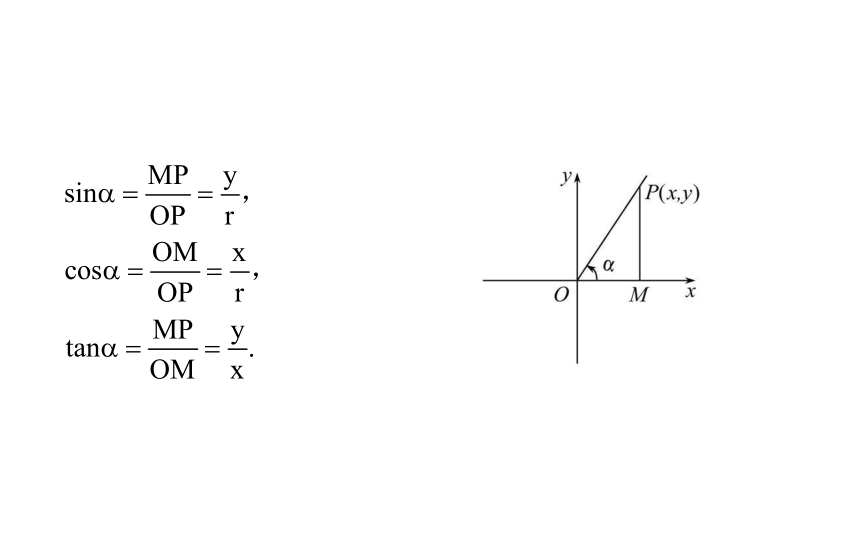







文档简介
课件51张PPT。7.2 任意角的三角函数
7.2.1 三角函数的定义1.三角函数的定义(坐标法)
在锐角的终边上任取一个不同于坐标原点的点P(x,y),
则r=|OP|= ,根据锐角三角函数定义写出锐角三
角函数的正弦、余弦、正切.【思考】
对于确定的角α,请问三角函数的结果会随点P在α终边上的位置的改变而改变吗?
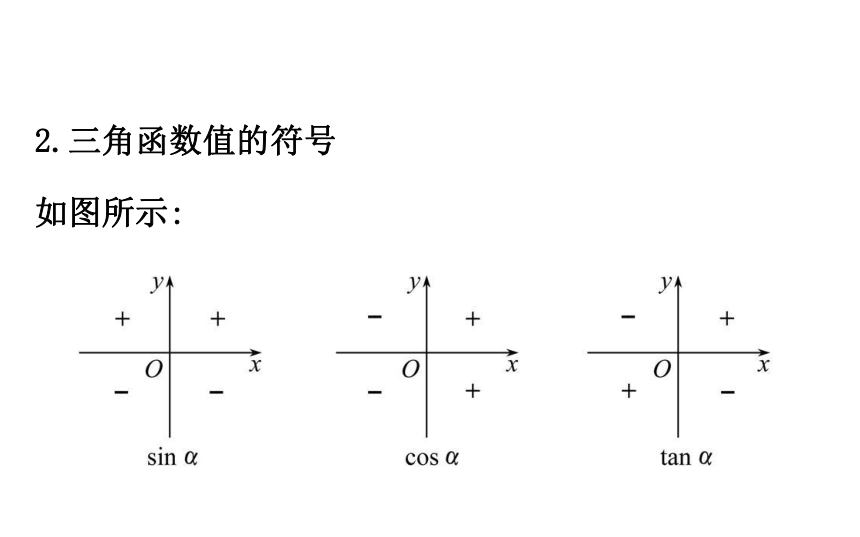
提示:根据相似三角形的知识,三角函数值不会随P点在终边上的位置的改变而改变.2.三角函数值的符号
如图所示:正弦:一二象限正,三四象限负;
余弦:一四象限正,二三象限负;
正切:一三象限正,二四象限负.【思考】
记忆正弦、余弦、正切在各象限的符号有什么诀窍吗?
提示:对正弦、余弦、正切函数值的符号可用下列口诀记忆:“一全正,二正弦,三正切,四余弦”,该口诀表示:第一象限全是正值,第二象限正弦是正值,第三象限正切是正值,第四象限余弦是正值.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)若sin α=sin β,则α=β. ( )
(2)设角α终边上的点P(x,y),r=|OP|≠0,则sin α= ,
且y越大,sin α的值越大. ( )
(3)终边落在y轴上的角的正切函数值为0. ( )提示:(1)×.由三角函数的定义知sin 0°=sin 360°
=0,此时0°≠360°.
(2)×.由任意角的正弦函数的定义知,sin α= .但
y变化时,sin α是定值.
(3)×.终边落在y轴上的角的正切函数值不存在.2.已知sin α>0,cos α<0,则角α是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角【解析】选B.由sin α>0,则α在一、二象限,由
cos α<0,则α在第二、三象限,故角α是第二象限角.3.已知角α的终边经过点(3,-4),则sin α+cos α的值为________.?【解析】易知r= =5,所以sin α=- ,
cos α= ,故sin α+cos α=- .
答案:- 类型一 三角函数的定义及应用
【典例】1.若角θ的终边过点P(a,8),且cos θ=- ,则a的值是 ( )
A.6 B.-6 C.10 D.-102.已知角α的终边落在直线 x+y=0上,求sin α, cos α,tan α的值.【思维·引】1.根据三角函数的定义,先求出r,再根
据公式cos θ= 求a的值.
2.在α的终边上任选一点P(a,b),求出P到原点的距离
为r=|OP|= (r>0),则sin α= ,cos α=
,tan α= .【解析】1.选B.由任意角的三角函数的定义可知
解得a=±6.显然a=6时不成立,所以a=-6.2.直线 x+y=0,即y=- x,经过第二、四象限,在第
二象限取直线上的点(-1, ),则r= =2,
所以sin α= ,cos α=- ,tan α=- ;在第四
象限取直线上的点(1,- ),则r=
所以sin α=- 【类题·通】
已知一个角的一个三角函数值求参数的值
先求出r= ,再根据三角函数的定义求出参数的值,注意根据三角函数值确定参数的正负.【习练·破】
已知角α的终边过点P(12,a),且tan α= ,求
sin α+cos α的值.【解析】根据三角函数的定义,tan α=
所以a=5,所以P(12,5).这时r=13,
所以sin α= ,cos α= ,所以sin α+cos α=
.【加练·固】
已知θ终边上一点P(x,3)(x≠0),且cos θ= x,求sin θ,tan θ.【解析】由题意知r=|OP|=
由三角函数定义得cos θ=
又因为cos θ=
因为x≠0,所以x=±1.当x=1时,P(1,3),此时sin θ=
当x=-1时,P(-1,3),此时sin θ= 类型二 三角函数值符号的应用
【典例】1.若sin αtan α<0,且 <0,则角α
是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角2.判断下列各式的符号:
(1)sin 145°cos(-210°);
(2)sin 3·cos 4·tan 5.【思维·引】1.先根据sin αtan α<0,确定角α的
范围,再根据 <0,确定角α的范围,两个范围取交
集最终确定角α的范围.
2.先判断已知角分别是第几象限角,再确定各三角函
数值的符号,最后判断乘积的符号.【解析】1.选C.由sin αtan α<0可知sin α,
tan α异号,从而α为第二、三象限角.
由 <0可知cos α,tan α异号,从而α为第三、四象限角.综上可知,α为第三象限角.2.(1)因为145°是第二象限角,所以sin 145°>0,
因为-210°=-360°+150°,所以-210°是第二象限角,
所以cos (-210°)<0,所以sin 145°cos (-210°)<0.
(2)因为 <3<π,π<4< <5<2π,
所以sin 3>0,cos 4<0,tan 5<0,
所以sin 3·cos 4·tan 5>0.【内化·悟】
怎样确定sin 3,cos 4等代数式的符号?
提示:当一个角没有带单位符号时,表示这个角是弧度制的角,我们需要先将弧度制化为角度制,不是特殊角时,利用π rad=180°或1 rad≈57.3°进行化简再确定三角函数值的符号.【类题·通】
判断三角函数值在各象限符号的攻略
(1)基础:准确确定三角函数值中各角所在象限;
(2)关键:准确记忆三角函数在各象限的符号;
(3)注意:用弧度制给出的角常常不写单位,不要误认为角度导致象限判断错误.
提醒:巧用口诀记忆三角函数值在各象限符号.【习练·破】
(1)在平面直角坐标系xOy中,角α以Ox为始边,终边经过点P(-1,m)(m≠0),则下列各式的值一定为负的是 ( )
A.sin α+cos α B.sin α-cos α
C.sin αcos α D. (2)判断下列各式的符号:
①tan 120°·sin 269°;②cos 4·tan 【解析】(1)选D.由已知得r=|OP|=
则sin α= ,cos α=- <0,tan α=-m.
所以 =cos α<0.故一定为负值的是D.(2)①因为120°是第二象限角,所以tan 120°<0.
因为269°是第三象限角,所以sin 269°<0.
所以tan 120°·sin 269°>0. ②因为π<4< ,所以4弧度是第三象限角,
所以cos 4<0.因为 所以- 是第一象
限角.所以tan >0.所以cos 4·tan <0.【加练·固】
1.已知点P(tan α,cos α)在第四象限,则角α终边在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.判断tan 191°-cos 191°的符号.【解析】1.选C.因为点P在第四象限,所以有
由此可判断角α终边在第三象限.
2.因为191°是第三象限角,所以tan 191°>0,
cos 191°<0.
所以tan 191°-cos 191°>0.类型三 三角函数定义的综合应用
角度1 三角函数的绝对值问题
【典例】设α是第三象限角,且 则
所在象限是 世纪金榜导学号( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【思维·引】先根据α在第三象限,用不等式表示α
的取值范围,再求 的取值范围,然后根据三角函数
值在各个象限的符号判断.【解析】选B.因为α是第三象限角,
所以2kπ+π<α<2kπ+ ,k∈Z.
所以kπ+
所以 在第二、四象限.又因为
所以cos <0.所以 在第二象限.【素养·探】
带绝对值的问题,关键是去绝对值,去绝对值时,要注意绝对值内代数式的正负,主要考查逻辑推理的核心素养.
当α为第二象限角时 的值是 ( )
A.1 B.0 C.2 D.-2【解析】选C.因为α为第二象限角,所以sin α>0,
cos α<0.
所以 角度2 分类讨论在三角函数中的应用
【典例】已知角α的终边上有一点P(24k,7k),k≠0,求sin α,cos α,tan α的值. 世纪金榜导学号【思维·引】已知角终边上的一点,求三角函数值,直接利用三角函数的定义;在利用定义时,求出的r带有参数,所以需要对参数先进行讨论.【解析】当k>0时,令x=24k,y=7k,
则有r=
所以sin α=
当k<0时,令x=24k,y=7k,则有r=-25k,
所以sin α= 【类题·通】
由三角函数的定义sin α= ,cos α= ,
tan α= ,(r>0),可知角的三角函数值的符号是由角终边上任一点P(x,y)的坐标确定的,当点P(x,y)的坐标中含有参数时,则需要先根据具体情况分类讨论,再进行计算求值.【习练·破】
函数y= 的值域是________.?【解析】由sin x≠0,cos x≠0知,x的终边不能落在
坐标轴上,当x为第一象限角时,sin x>0,cos x>0,
sin xcos x>0,y=0;当x为第二象限角时,sin x>0,
cos x<0,sin xcos x<0,y=2;当x为第三象限角时,
sin x<0,cos x<0,sin xcos x>0,y=-4;当x为第四
象限角时,sin x<0,cos x>0,sin xcos x<0,y=2.故函数y= 的值域为{-4,0,2}.
答案:{-4,0,2}
7.2.1 三角函数的定义1.三角函数的定义(坐标法)
在锐角的终边上任取一个不同于坐标原点的点P(x,y),
则r=|OP|= ,根据锐角三角函数定义写出锐角三
角函数的正弦、余弦、正切.【思考】
对于确定的角α,请问三角函数的结果会随点P在α终边上的位置的改变而改变吗?
提示:根据相似三角形的知识,三角函数值不会随P点在终边上的位置的改变而改变.2.三角函数值的符号
如图所示:正弦:一二象限正,三四象限负;
余弦:一四象限正,二三象限负;
正切:一三象限正,二四象限负.【思考】
记忆正弦、余弦、正切在各象限的符号有什么诀窍吗?
提示:对正弦、余弦、正切函数值的符号可用下列口诀记忆:“一全正,二正弦,三正切,四余弦”,该口诀表示:第一象限全是正值,第二象限正弦是正值,第三象限正切是正值,第四象限余弦是正值.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)若sin α=sin β,则α=β. ( )
(2)设角α终边上的点P(x,y),r=|OP|≠0,则sin α= ,
且y越大,sin α的值越大. ( )
(3)终边落在y轴上的角的正切函数值为0. ( )提示:(1)×.由三角函数的定义知sin 0°=sin 360°
=0,此时0°≠360°.
(2)×.由任意角的正弦函数的定义知,sin α= .但
y变化时,sin α是定值.
(3)×.终边落在y轴上的角的正切函数值不存在.2.已知sin α>0,cos α<0,则角α是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角【解析】选B.由sin α>0,则α在一、二象限,由
cos α<0,则α在第二、三象限,故角α是第二象限角.3.已知角α的终边经过点(3,-4),则sin α+cos α的值为________.?【解析】易知r= =5,所以sin α=- ,
cos α= ,故sin α+cos α=- .
答案:- 类型一 三角函数的定义及应用
【典例】1.若角θ的终边过点P(a,8),且cos θ=- ,则a的值是 ( )
A.6 B.-6 C.10 D.-102.已知角α的终边落在直线 x+y=0上,求sin α, cos α,tan α的值.【思维·引】1.根据三角函数的定义,先求出r,再根
据公式cos θ= 求a的值.
2.在α的终边上任选一点P(a,b),求出P到原点的距离
为r=|OP|= (r>0),则sin α= ,cos α=
,tan α= .【解析】1.选B.由任意角的三角函数的定义可知
解得a=±6.显然a=6时不成立,所以a=-6.2.直线 x+y=0,即y=- x,经过第二、四象限,在第
二象限取直线上的点(-1, ),则r= =2,
所以sin α= ,cos α=- ,tan α=- ;在第四
象限取直线上的点(1,- ),则r=
所以sin α=- 【类题·通】
已知一个角的一个三角函数值求参数的值
先求出r= ,再根据三角函数的定义求出参数的值,注意根据三角函数值确定参数的正负.【习练·破】
已知角α的终边过点P(12,a),且tan α= ,求
sin α+cos α的值.【解析】根据三角函数的定义,tan α=
所以a=5,所以P(12,5).这时r=13,
所以sin α= ,cos α= ,所以sin α+cos α=
.【加练·固】
已知θ终边上一点P(x,3)(x≠0),且cos θ= x,求sin θ,tan θ.【解析】由题意知r=|OP|=
由三角函数定义得cos θ=
又因为cos θ=
因为x≠0,所以x=±1.当x=1时,P(1,3),此时sin θ=
当x=-1时,P(-1,3),此时sin θ= 类型二 三角函数值符号的应用
【典例】1.若sin αtan α<0,且 <0,则角α
是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角2.判断下列各式的符号:
(1)sin 145°cos(-210°);
(2)sin 3·cos 4·tan 5.【思维·引】1.先根据sin αtan α<0,确定角α的
范围,再根据 <0,确定角α的范围,两个范围取交
集最终确定角α的范围.
2.先判断已知角分别是第几象限角,再确定各三角函
数值的符号,最后判断乘积的符号.【解析】1.选C.由sin αtan α<0可知sin α,
tan α异号,从而α为第二、三象限角.
由 <0可知cos α,tan α异号,从而α为第三、四象限角.综上可知,α为第三象限角.2.(1)因为145°是第二象限角,所以sin 145°>0,
因为-210°=-360°+150°,所以-210°是第二象限角,
所以cos (-210°)<0,所以sin 145°cos (-210°)<0.
(2)因为 <3<π,π<4< <5<2π,
所以sin 3>0,cos 4<0,tan 5<0,
所以sin 3·cos 4·tan 5>0.【内化·悟】
怎样确定sin 3,cos 4等代数式的符号?
提示:当一个角没有带单位符号时,表示这个角是弧度制的角,我们需要先将弧度制化为角度制,不是特殊角时,利用π rad=180°或1 rad≈57.3°进行化简再确定三角函数值的符号.【类题·通】
判断三角函数值在各象限符号的攻略
(1)基础:准确确定三角函数值中各角所在象限;
(2)关键:准确记忆三角函数在各象限的符号;
(3)注意:用弧度制给出的角常常不写单位,不要误认为角度导致象限判断错误.
提醒:巧用口诀记忆三角函数值在各象限符号.【习练·破】
(1)在平面直角坐标系xOy中,角α以Ox为始边,终边经过点P(-1,m)(m≠0),则下列各式的值一定为负的是 ( )
A.sin α+cos α B.sin α-cos α
C.sin αcos α D. (2)判断下列各式的符号:
①tan 120°·sin 269°;②cos 4·tan 【解析】(1)选D.由已知得r=|OP|=
则sin α= ,cos α=- <0,tan α=-m.
所以 =cos α<0.故一定为负值的是D.(2)①因为120°是第二象限角,所以tan 120°<0.
因为269°是第三象限角,所以sin 269°<0.
所以tan 120°·sin 269°>0. ②因为π<4< ,所以4弧度是第三象限角,
所以cos 4<0.因为 所以- 是第一象
限角.所以tan >0.所以cos 4·tan <0.【加练·固】
1.已知点P(tan α,cos α)在第四象限,则角α终边在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.判断tan 191°-cos 191°的符号.【解析】1.选C.因为点P在第四象限,所以有
由此可判断角α终边在第三象限.
2.因为191°是第三象限角,所以tan 191°>0,
cos 191°<0.
所以tan 191°-cos 191°>0.类型三 三角函数定义的综合应用
角度1 三角函数的绝对值问题
【典例】设α是第三象限角,且 则
所在象限是 世纪金榜导学号( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限【思维·引】先根据α在第三象限,用不等式表示α
的取值范围,再求 的取值范围,然后根据三角函数
值在各个象限的符号判断.【解析】选B.因为α是第三象限角,
所以2kπ+π<α<2kπ+ ,k∈Z.
所以kπ+
所以 在第二、四象限.又因为
所以cos <0.所以 在第二象限.【素养·探】
带绝对值的问题,关键是去绝对值,去绝对值时,要注意绝对值内代数式的正负,主要考查逻辑推理的核心素养.
当α为第二象限角时 的值是 ( )
A.1 B.0 C.2 D.-2【解析】选C.因为α为第二象限角,所以sin α>0,
cos α<0.
所以 角度2 分类讨论在三角函数中的应用
【典例】已知角α的终边上有一点P(24k,7k),k≠0,求sin α,cos α,tan α的值. 世纪金榜导学号【思维·引】已知角终边上的一点,求三角函数值,直接利用三角函数的定义;在利用定义时,求出的r带有参数,所以需要对参数先进行讨论.【解析】当k>0时,令x=24k,y=7k,
则有r=
所以sin α=
当k<0时,令x=24k,y=7k,则有r=-25k,
所以sin α= 【类题·通】
由三角函数的定义sin α= ,cos α= ,
tan α= ,(r>0),可知角的三角函数值的符号是由角终边上任一点P(x,y)的坐标确定的,当点P(x,y)的坐标中含有参数时,则需要先根据具体情况分类讨论,再进行计算求值.【习练·破】
函数y= 的值域是________.?【解析】由sin x≠0,cos x≠0知,x的终边不能落在
坐标轴上,当x为第一象限角时,sin x>0,cos x>0,
sin xcos x>0,y=0;当x为第二象限角时,sin x>0,
cos x<0,sin xcos x<0,y=2;当x为第三象限角时,
sin x<0,cos x<0,sin xcos x>0,y=-4;当x为第四
象限角时,sin x<0,cos x>0,sin xcos x<0,y=2.故函数y= 的值域为{-4,0,2}.
答案:{-4,0,2}
