新教材人教B版数学必修第三册课件:7.2.2 单位圆与三角函数线(43张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.2.2 单位圆与三角函数线(43张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 10:32:37 | ||
图片预览











文档简介
课件43张PPT。7.2.2
单位圆与三角函数线1.单位圆与三角函数
(1)单位圆:在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合.
(2)三角函数与单位圆:角α的终边与单位圆相交于点P(x,y),如图:则sin α=y,cos α=x,tan α= ,
则角α的终边与单位圆的交点为P(cos α,sin α).?【思考】
单位圆的圆心和半径分别是什么?
提示:单位圆的圆心在原点,半径为单位长度即半径等于1.2.三角函数线
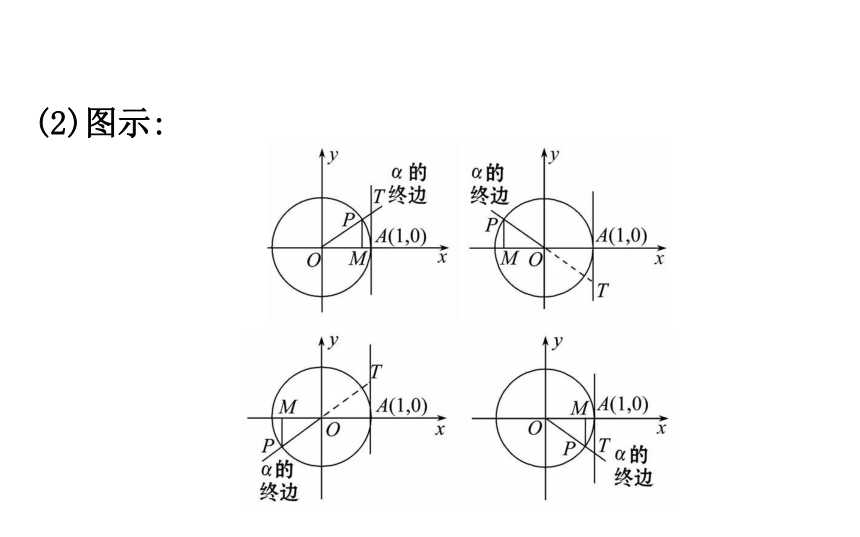
(1)作图:①角α的终边与单位圆交于P,过P作PM垂直于x轴,垂足为M.
②过A(1,0)作x轴的垂线,交角α的终边或其反向延长线于点T.(2)图示:(3)结论:向量 分别称为角α的正弦线、余弦线、正切线,统称为三角函数线.【思考】
(1)三角函数线的长度与三角函数的值有何关系?
提示:三角函数线的长度等于三角函数值的绝对值. (2)三角函数线的方向能表示三角函数的正负吗?请说明理由.
提示:能,当三角函数线与x轴(或y轴)正向同向时,所表示三角函数值为正的,与x轴(或y轴)正向反向时,所表示三角函数值为负的.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)角α的正弦线的长度等于sin α. ( )
(2)对任意角都能作出正弦线、余弦线和正切线. ( )
(3)余弦线和正切线的始点都是原点. ( )提示: (1)×.角α的正弦线的长度等于|sin α|.
(2)×.90°角不能作正切线.
(3)×.正切线的始点是(1,0).2.如图,在单位圆中角α的正弦线、正切线完全正确的是 ( )【解析】选C.α为第三象限角,故正弦线为 ,正切
线为 ,C正确.3.角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异,那么α的值为 ( )【解析】选D.根据三角函数值的符号可知,当角α在
二、四象限时,角α的正弦、余弦符号相反.又角α的
正、余弦线的长度相等,0<α<2π,所以α= .4.角 的终边与单位圆的交点的坐标是________.?【解析】由于角 的终边与单位圆的交点横坐标是
纵坐标是
所以角 的终边与单位圆的交点的坐标是
答案: 类型一 三角函数线的作法及应用
【典例】1.角 有相同的 ( )
A.正弦线 B.余弦线
C.正切线 D.不能确定
2.求作 的正弦线、余弦线和正切线.【思维·引】1.在同一个平面直角坐标系中分别作出
角 的三角函数线,比较可得.
2.作出平面直角坐标系,作出角 的终边,分别作出
它的正弦线、余弦线、正切线即可.【解析】1.选C.角 的终边互为反向延长线,所以正切线相同.2.角 的终边(如图)与单位圆的交点为P.作PM垂直
于x轴,垂足为M,过A(1,0)作单位圆的切线AT,与 的
终边的反向延长线交于点T,则 的正弦线为 ,余
弦线为 ,正切线为 .【内化·悟】
作角的正弦线、余弦线时注意哪些问题?
提示:作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.【类题·通】
三角函数线的作法步骤
(1)作直角坐标系和角的终边.
(2)作单位圆,圆与角的终边的交点为P,与x轴正半轴的交点为A.(3)过点P作x轴的垂线,垂足为M.
(4)过点A作x轴的垂线,与角的终边或其反向延长线交于点T.
(5)即向量 分别为角的正弦线,余弦线和正切线. 【习练·破】
1.已知角α的正弦线的长度为单位长度,那么角α的终边 ( )
A.在x轴上 B.在y轴上
C.在直线y=x上 D.在直线y=-x上【解析】选B.根据正弦线的定义知,|sin α|=1,所以sin α=±1,所以角α的终边在y轴上.2.作出- 的正弦线、余弦线和正切线.【解析】如图所示,所以角- 的正弦线为 ,余弦
线为 ,正切线为 .类型二 三角函数线的综合应用
角度1 利用三角函数线比较大小
【典例】比较下列各组数的大小.【思维·引】在单位圆中正确画出各角的需要比较大小的三角函数线.【解析】(1)如图,在单位圆中作出 的余弦
线
因为 的
余弦均为负数,
所以 (2)如图,分别作出 的正弦线和正切线,
由图知,角 的正弦线和正切线分别为 因为
且 的正弦和正切均为正数,所以tan
>sin .【素养·探】
利用三角函数线比较大小,常常涉及直观想象的核心素养.
利用三角函数线比较大小的步骤:
①角的位置要“对号入座”.
②比较三角函数线的长度.
③确定三角函数值的正负.将本例中的条件改为“ ”,则a,b,c的大小顺序排列为________.?【解析】由如图的三角函数线知:
因为
所以 所以b答案:b【典例】若α是第一象限角,则sin α+cos α的值与1的大小关系是 世纪金榜导学号( )
A.sin α+cos α>1 B.sin α+cos α=1
C.sin α+cos α<1 D.不能确定【思维·引】画出三角函数线,根据三角形两边之和大于第三边,即可得到答案.【解析】选A.如图,角α的终边与单位圆交于P点,过P作PM⊥x轴于M点,由三角形两边之和大于第三边可知sin α+cos α>1.【类题·通】
利用三角函数线比较函数值大小的关键及注意点
(1)关键:在单位圆中作出所要比较的角的三角函数线.
(2)注意点:比较大小,既要注意三角函数线的长短,又要注意方向.【习练·破】
若α是三角形的内角,且sin α+cos α= ,则这个三角形是 ( )
A.等边三角形 B.直角三角形
C.锐角三角形 D.钝角三角形【解析】选D.当0<α≤ 时,由单位圆中的三角函数
线知,sin α+cos α≥1,而sin α+cos α= ,所以
α必为钝角.
单位圆与三角函数线1.单位圆与三角函数
(1)单位圆:在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合.
(2)三角函数与单位圆:角α的终边与单位圆相交于点P(x,y),如图:则sin α=y,cos α=x,tan α= ,
则角α的终边与单位圆的交点为P(cos α,sin α).?【思考】
单位圆的圆心和半径分别是什么?
提示:单位圆的圆心在原点,半径为单位长度即半径等于1.2.三角函数线
(1)作图:①角α的终边与单位圆交于P,过P作PM垂直于x轴,垂足为M.
②过A(1,0)作x轴的垂线,交角α的终边或其反向延长线于点T.(2)图示:(3)结论:向量 分别称为角α的正弦线、余弦线、正切线,统称为三角函数线.【思考】
(1)三角函数线的长度与三角函数的值有何关系?
提示:三角函数线的长度等于三角函数值的绝对值. (2)三角函数线的方向能表示三角函数的正负吗?请说明理由.
提示:能,当三角函数线与x轴(或y轴)正向同向时,所表示三角函数值为正的,与x轴(或y轴)正向反向时,所表示三角函数值为负的.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)角α的正弦线的长度等于sin α. ( )
(2)对任意角都能作出正弦线、余弦线和正切线. ( )
(3)余弦线和正切线的始点都是原点. ( )提示: (1)×.角α的正弦线的长度等于|sin α|.
(2)×.90°角不能作正切线.
(3)×.正切线的始点是(1,0).2.如图,在单位圆中角α的正弦线、正切线完全正确的是 ( )【解析】选C.α为第三象限角,故正弦线为 ,正切
线为 ,C正确.3.角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异,那么α的值为 ( )【解析】选D.根据三角函数值的符号可知,当角α在
二、四象限时,角α的正弦、余弦符号相反.又角α的
正、余弦线的长度相等,0<α<2π,所以α= .4.角 的终边与单位圆的交点的坐标是________.?【解析】由于角 的终边与单位圆的交点横坐标是
纵坐标是
所以角 的终边与单位圆的交点的坐标是
答案: 类型一 三角函数线的作法及应用
【典例】1.角 有相同的 ( )
A.正弦线 B.余弦线
C.正切线 D.不能确定
2.求作 的正弦线、余弦线和正切线.【思维·引】1.在同一个平面直角坐标系中分别作出
角 的三角函数线,比较可得.
2.作出平面直角坐标系,作出角 的终边,分别作出
它的正弦线、余弦线、正切线即可.【解析】1.选C.角 的终边互为反向延长线,所以正切线相同.2.角 的终边(如图)与单位圆的交点为P.作PM垂直
于x轴,垂足为M,过A(1,0)作单位圆的切线AT,与 的
终边的反向延长线交于点T,则 的正弦线为 ,余
弦线为 ,正切线为 .【内化·悟】
作角的正弦线、余弦线时注意哪些问题?
提示:作正弦线、余弦线时,首先找到角的终边与单位圆的交点,然后过此交点作x轴的垂线,得到垂足,从而得正弦线和余弦线.【类题·通】
三角函数线的作法步骤
(1)作直角坐标系和角的终边.
(2)作单位圆,圆与角的终边的交点为P,与x轴正半轴的交点为A.(3)过点P作x轴的垂线,垂足为M.
(4)过点A作x轴的垂线,与角的终边或其反向延长线交于点T.
(5)即向量 分别为角的正弦线,余弦线和正切线. 【习练·破】
1.已知角α的正弦线的长度为单位长度,那么角α的终边 ( )
A.在x轴上 B.在y轴上
C.在直线y=x上 D.在直线y=-x上【解析】选B.根据正弦线的定义知,|sin α|=1,所以sin α=±1,所以角α的终边在y轴上.2.作出- 的正弦线、余弦线和正切线.【解析】如图所示,所以角- 的正弦线为 ,余弦
线为 ,正切线为 .类型二 三角函数线的综合应用
角度1 利用三角函数线比较大小
【典例】比较下列各组数的大小.【思维·引】在单位圆中正确画出各角的需要比较大小的三角函数线.【解析】(1)如图,在单位圆中作出 的余弦
线
因为 的
余弦均为负数,
所以 (2)如图,分别作出 的正弦线和正切线,
由图知,角 的正弦线和正切线分别为 因为
且 的正弦和正切均为正数,所以tan
>sin .【素养·探】
利用三角函数线比较大小,常常涉及直观想象的核心素养.
利用三角函数线比较大小的步骤:
①角的位置要“对号入座”.
②比较三角函数线的长度.
③确定三角函数值的正负.将本例中的条件改为“ ”,则a,b,c的大小顺序排列为________.?【解析】由如图的三角函数线知:
因为
所以 所以b
A.sin α+cos α>1 B.sin α+cos α=1
C.sin α+cos α<1 D.不能确定【思维·引】画出三角函数线,根据三角形两边之和大于第三边,即可得到答案.【解析】选A.如图,角α的终边与单位圆交于P点,过P作PM⊥x轴于M点,由三角形两边之和大于第三边可知sin α+cos α>1.【类题·通】
利用三角函数线比较函数值大小的关键及注意点
(1)关键:在单位圆中作出所要比较的角的三角函数线.
(2)注意点:比较大小,既要注意三角函数线的长短,又要注意方向.【习练·破】
若α是三角形的内角,且sin α+cos α= ,则这个三角形是 ( )
A.等边三角形 B.直角三角形
C.锐角三角形 D.钝角三角形【解析】选D.当0<α≤ 时,由单位圆中的三角函数
线知,sin α+cos α≥1,而sin α+cos α= ,所以
α必为钝角.
