新教材人教B版数学必修第三册课件:7.2.4 诱导公式(二)(57张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.2.4 诱导公式(二)(57张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 10:34:40 | ||
图片预览




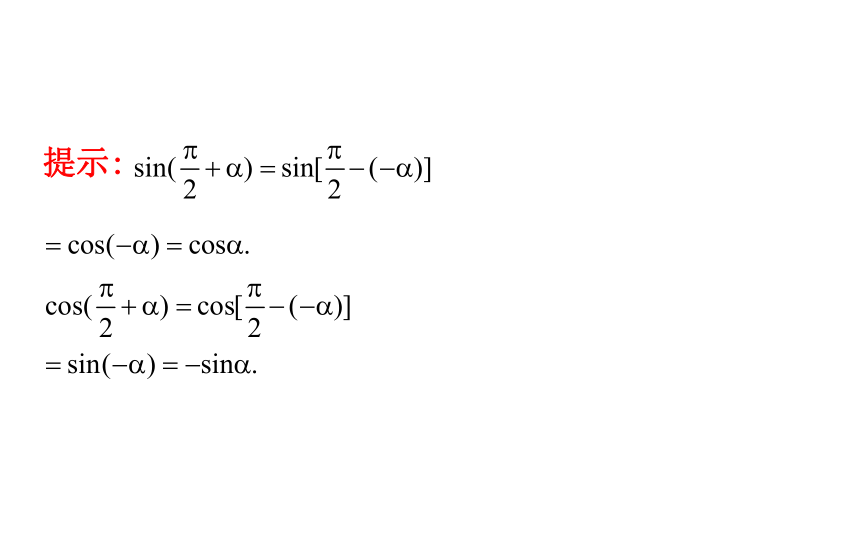

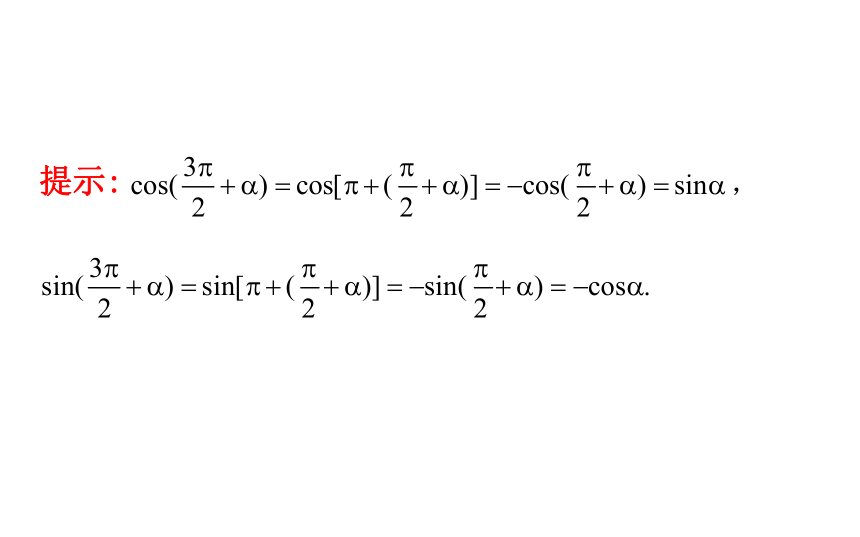
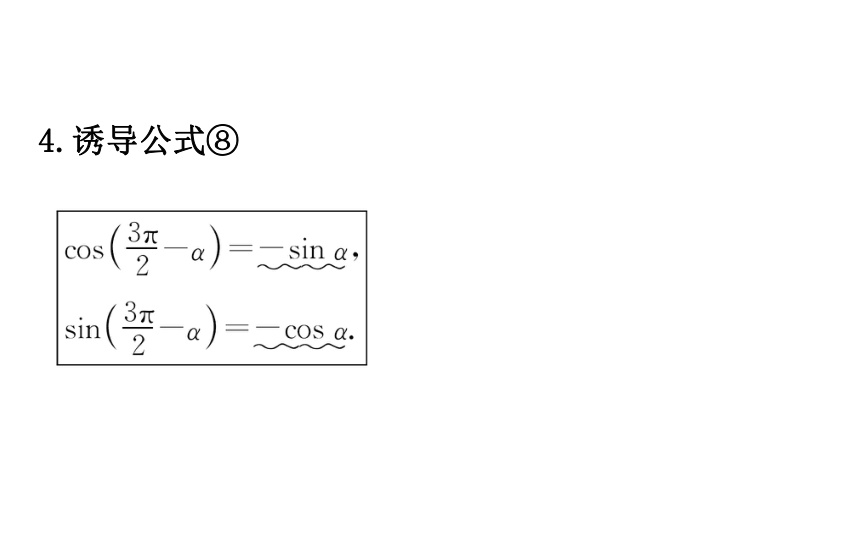
文档简介
课件57张PPT。7.2.4
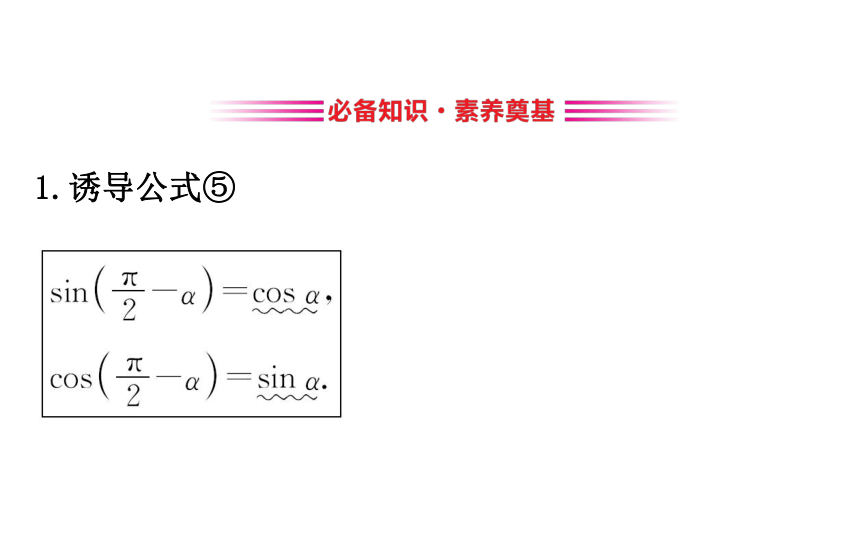
诱导公式(二)1.诱导公式⑤【思考】
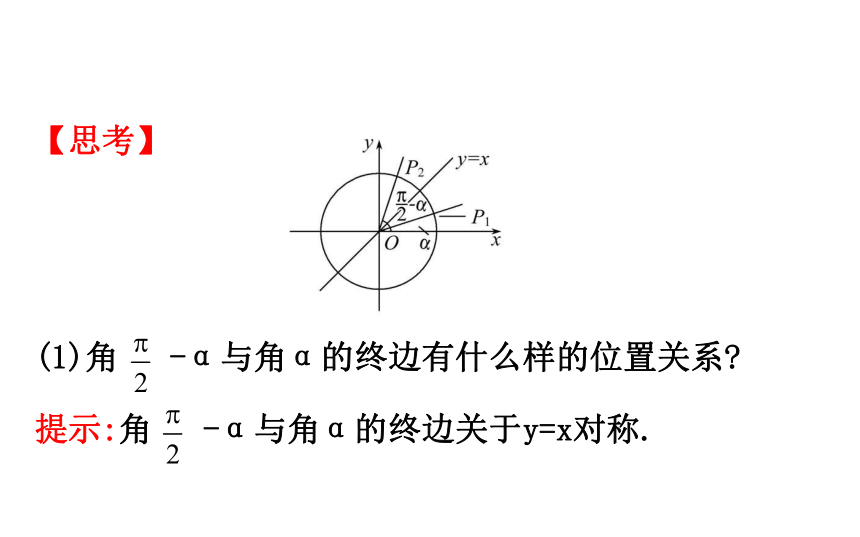
(1)角 -α与角α的终边有什么样的位置关系?
提示:角 -α与角α的终边关于y=x对称. (2)点P1(a,b)关于y=x对称的对称点坐标是什么?
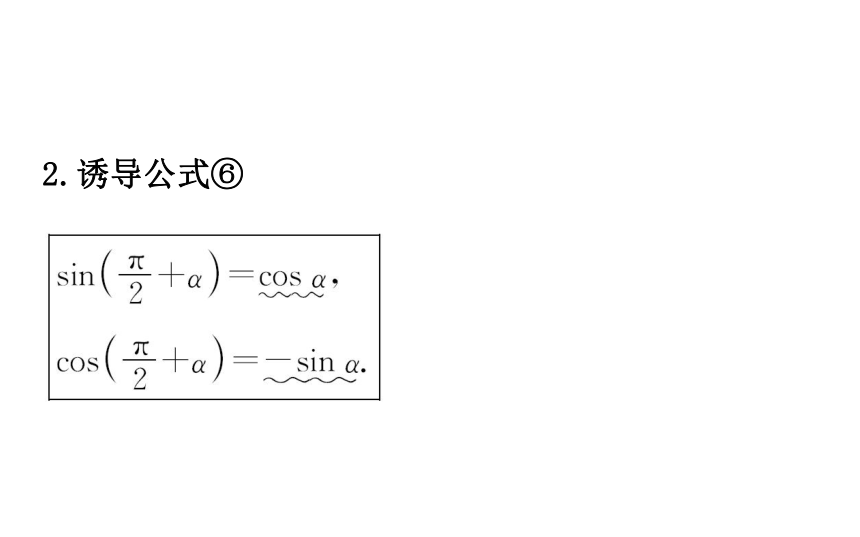
提示:点P1(a,b)关于y=x对称的对称点坐标是P2(b,a).2.诱导公式⑥【思考】
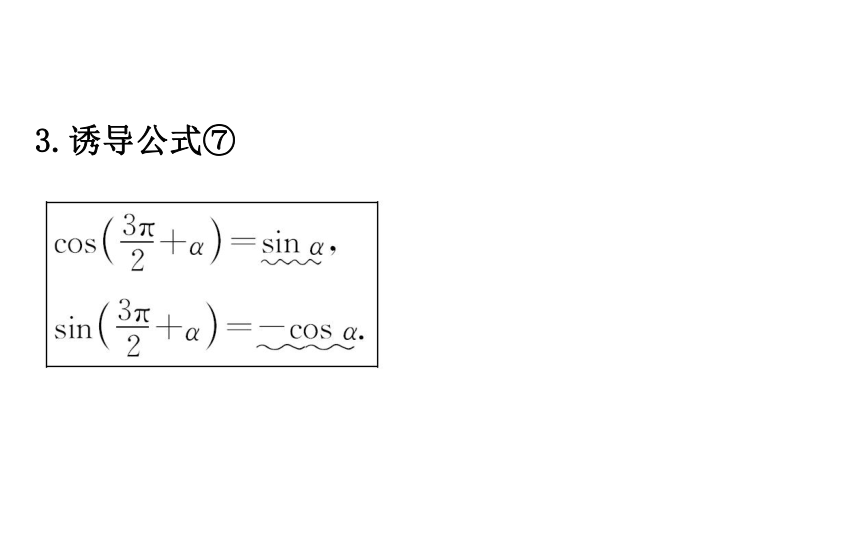
如何由公式②、公式⑤推导公式⑥?提示: 3.诱导公式⑦【思考】
如何推导公式⑦?提示:4.诱导公式⑧【思考】
如何理解诱导公式⑤⑥⑦⑧?提示:(1)函数名称: ±α的正弦(余弦)函数值,分别转化为α的余弦(正弦)函数值.
(2)符号:函数值前面加上一个把α看成锐角时原函数值的符号.
(3)作用:利用诱导公式⑤⑥⑦⑧,可以实现正弦函数与余弦函数的相互转化.
(4)简记:“函数名改变,符号看象限”.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)sin(90°+α)=-cos α. ( )
(2)在△ABC中, ( )
(3)sin =±cos α. ( )提示:(1)×.由诱导公式⑥知sin(90°+α)=cos α.
(2)√.因为 由诱导公式⑤可知
(3)×.例如当k=2时,sin =sin(π-α)=
sin α≠±cos α.2.sin 95°+cos 175°的值为 ( )
A.sin 5° B.1
C.0 D.2sin 5°【解析】选C.sin 95°=sin(90°+5°)=cos 5°,
cos 175°=cos(180°-5°)=-cos 5°,故sin 95°+
cos 175°=cos 5°-cos 5°=0.3.若 =( )【解析】选D.因为
所以sin α=
所以 4.若cos(π+α)= ,则sin =________.?【解析】方法一:cos(π+α)=-cos α= ,
所以cos α=- ,
方法二:cos(π+α)=
所以
所以
答案:- 类型一 利用诱导公式求值
【典例】1.已知cos 31°=m,则sin 239°tan 149°的值是 ( )2.已知cos(π+α)=- ,α为第一象限角,则cos
的值为________.?
3.已知 ,则cos 的值为________.?【思维·引】1.239°=270°-31°,149°=180°-
31°.
2.利用诱导公式化简计算.
3. 【解析】1.选B.sin 239°tan 149°
=sin(270°-31°)·tan(180°-31°)
=-cos 31°·(-tan 31°)=sin 31°2.因为cos(π+α)=-cos α=- ,
所以cos α= ,又α为第一象限角,
则
答案:- 3.
答案: 【内化·悟】
对于含有参变量的已知角和未知角怎样转化?
提示:通常把含有参变量的两个式子进行加减运算,从而发现互补、互余关系.【类题·通】
解决化简求值问题的策略
(1)首先要仔细观察条件式与所求式之间的关系,发现它们的互补、互余关系.(2)可以将已知式进行变形,向所求式转化,或将所求
式进行变形,向已知式转化.
提醒:常见的互余关系有: -α与 +α, +α与
-α等;常见的互补关系有: +θ与 -θ,
+θ与 -θ等. 【习练·破】
1.已知sin 40°=a,则cos 130°等于 ( )【解析】选B.cos 130°=cos(90°+40°)=
-sin 40°=-a.2.已知sin(75°+α)= ,则cos(15°-α)的值
为 ( )【解析】选C.因为(75°+α)+(15°-α)=90°,
所以cos(15°-α)=cos[90°-(75°+α)]
=sin(75°+α)= .类型二 利用诱导公式化简、证明
【典例】求证 =-tan α. 世纪金榜导学号【思维·引】等式左边含有k· ±α,k∈Z的形式的角,可以利用诱导公式直接对等式左边进行化简,从而推得等式右边.【证明】因为左边=
所以原等式成立.【内化·悟】
利用诱导公式化简的基本原则是什么?
提示:(1)负化正、大化小、小化锐、锐求值.
(2)对于k· ±α,k∈Z的形式的角,记准:奇变偶不变,符号看象限.【类题·通】
对于恒等式的证明,应遵循化繁为简的原则,从左边推导右边或从右边推导左边,也可以左右归一,变更论证的方法.常用定义法、弦化切、拆项拆角法、“1”的代换法、公式变形法等,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.【习练·破】
证明:【证明】左边=
所以原式成立.【加练·固】
化简: 【解析】原式= 类型三 诱导公式的综合应用
【典例】已知f(α)=
世纪金榜导学号
(1)化简f(α).
(2)若f(α)= ,求sin α+cos α的值.【思维·引】利用诱导公式对函数式进行化简,再利用平方关系等三角函数知识解题.【解析】(1)f(α)=(2)若f(α)= ,则sin α= ,cos2α=1-sin2α
= .
当α为第一象限角时,cos α= ,sin α+cos α=
当α为第二象限角时,cos α=- ,sin α+cos α= 【内化·悟】
对于复杂的、综合性很强的三角函数化简计算、求值问题怎样解决?提示:运用诱导公式化简:求值的前提是熟记诱导公式,
诱导公式可以概括为一句口诀:“奇变偶不变,符号看
象限”;即把已知角统一写成“k· ±α,k∈Z”的
形式,根据k的奇偶性选择函数名进行化简,再综合利
用三角函数的定义,特殊角的三角函数等知识解决问
题.【类题·通】
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形.【习练·破】
已知
(1)化简f(α).
(2)若角A是△ABC的内角,且f(A)= ,求tan A-sin A的值.【解析】(1)f(α)=
(2)因为f(A)=cos A= ,又A为△ABC的内角,
所以由平方关系,得sin A=
所以tan A=
所以tan A-sin A= 【加练·固】
已知sin θ,cos θ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求 的值.
(2)求tan(π-θ)- 的值.【解析】由已知原方程判别式Δ≥0,
即(-a)2-4a≥0,则a≥4或a≤0.
又
(sin θ+cos θ)2=1+2sin θcos θ,
即a2-2a-1=0,所以a=1- 或a=1+ (舍去).
则sin θ+cos θ=sin θcos θ=1- .
诱导公式(二)1.诱导公式⑤【思考】
(1)角 -α与角α的终边有什么样的位置关系?
提示:角 -α与角α的终边关于y=x对称. (2)点P1(a,b)关于y=x对称的对称点坐标是什么?
提示:点P1(a,b)关于y=x对称的对称点坐标是P2(b,a).2.诱导公式⑥【思考】
如何由公式②、公式⑤推导公式⑥?提示: 3.诱导公式⑦【思考】
如何推导公式⑦?提示:4.诱导公式⑧【思考】
如何理解诱导公式⑤⑥⑦⑧?提示:(1)函数名称: ±α的正弦(余弦)函数值,分别转化为α的余弦(正弦)函数值.
(2)符号:函数值前面加上一个把α看成锐角时原函数值的符号.
(3)作用:利用诱导公式⑤⑥⑦⑧,可以实现正弦函数与余弦函数的相互转化.
(4)简记:“函数名改变,符号看象限”.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)sin(90°+α)=-cos α. ( )
(2)在△ABC中, ( )
(3)sin =±cos α. ( )提示:(1)×.由诱导公式⑥知sin(90°+α)=cos α.
(2)√.因为 由诱导公式⑤可知
(3)×.例如当k=2时,sin =sin(π-α)=
sin α≠±cos α.2.sin 95°+cos 175°的值为 ( )
A.sin 5° B.1
C.0 D.2sin 5°【解析】选C.sin 95°=sin(90°+5°)=cos 5°,
cos 175°=cos(180°-5°)=-cos 5°,故sin 95°+
cos 175°=cos 5°-cos 5°=0.3.若 =( )【解析】选D.因为
所以sin α=
所以 4.若cos(π+α)= ,则sin =________.?【解析】方法一:cos(π+α)=-cos α= ,
所以cos α=- ,
方法二:cos(π+α)=
所以
所以
答案:- 类型一 利用诱导公式求值
【典例】1.已知cos 31°=m,则sin 239°tan 149°的值是 ( )2.已知cos(π+α)=- ,α为第一象限角,则cos
的值为________.?
3.已知 ,则cos 的值为________.?【思维·引】1.239°=270°-31°,149°=180°-
31°.
2.利用诱导公式化简计算.
3. 【解析】1.选B.sin 239°tan 149°
=sin(270°-31°)·tan(180°-31°)
=-cos 31°·(-tan 31°)=sin 31°2.因为cos(π+α)=-cos α=- ,
所以cos α= ,又α为第一象限角,
则
答案:- 3.
答案: 【内化·悟】
对于含有参变量的已知角和未知角怎样转化?
提示:通常把含有参变量的两个式子进行加减运算,从而发现互补、互余关系.【类题·通】
解决化简求值问题的策略
(1)首先要仔细观察条件式与所求式之间的关系,发现它们的互补、互余关系.(2)可以将已知式进行变形,向所求式转化,或将所求
式进行变形,向已知式转化.
提醒:常见的互余关系有: -α与 +α, +α与
-α等;常见的互补关系有: +θ与 -θ,
+θ与 -θ等. 【习练·破】
1.已知sin 40°=a,则cos 130°等于 ( )【解析】选B.cos 130°=cos(90°+40°)=
-sin 40°=-a.2.已知sin(75°+α)= ,则cos(15°-α)的值
为 ( )【解析】选C.因为(75°+α)+(15°-α)=90°,
所以cos(15°-α)=cos[90°-(75°+α)]
=sin(75°+α)= .类型二 利用诱导公式化简、证明
【典例】求证 =-tan α. 世纪金榜导学号【思维·引】等式左边含有k· ±α,k∈Z的形式的角,可以利用诱导公式直接对等式左边进行化简,从而推得等式右边.【证明】因为左边=
所以原等式成立.【内化·悟】
利用诱导公式化简的基本原则是什么?
提示:(1)负化正、大化小、小化锐、锐求值.
(2)对于k· ±α,k∈Z的形式的角,记准:奇变偶不变,符号看象限.【类题·通】
对于恒等式的证明,应遵循化繁为简的原则,从左边推导右边或从右边推导左边,也可以左右归一,变更论证的方法.常用定义法、弦化切、拆项拆角法、“1”的代换法、公式变形法等,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.【习练·破】
证明:【证明】左边=
所以原式成立.【加练·固】
化简: 【解析】原式= 类型三 诱导公式的综合应用
【典例】已知f(α)=
世纪金榜导学号
(1)化简f(α).
(2)若f(α)= ,求sin α+cos α的值.【思维·引】利用诱导公式对函数式进行化简,再利用平方关系等三角函数知识解题.【解析】(1)f(α)=(2)若f(α)= ,则sin α= ,cos2α=1-sin2α
= .
当α为第一象限角时,cos α= ,sin α+cos α=
当α为第二象限角时,cos α=- ,sin α+cos α= 【内化·悟】
对于复杂的、综合性很强的三角函数化简计算、求值问题怎样解决?提示:运用诱导公式化简:求值的前提是熟记诱导公式,
诱导公式可以概括为一句口诀:“奇变偶不变,符号看
象限”;即把已知角统一写成“k· ±α,k∈Z”的
形式,根据k的奇偶性选择函数名进行化简,再综合利
用三角函数的定义,特殊角的三角函数等知识解决问
题.【类题·通】
诱导公式综合应用要“三看”
一看角:①化大为小;②看角与角间的联系,可通过相加、相减分析两角的关系.二看函数名称:一般是弦切互化.
三看式子结构:通过分析式子,选择合适的方法,如分式可对分子分母同乘一个式子变形.【习练·破】
已知
(1)化简f(α).
(2)若角A是△ABC的内角,且f(A)= ,求tan A-sin A的值.【解析】(1)f(α)=
(2)因为f(A)=cos A= ,又A为△ABC的内角,
所以由平方关系,得sin A=
所以tan A=
所以tan A-sin A= 【加练·固】
已知sin θ,cos θ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求 的值.
(2)求tan(π-θ)- 的值.【解析】由已知原方程判别式Δ≥0,
即(-a)2-4a≥0,则a≥4或a≤0.
又
(sin θ+cos θ)2=1+2sin θcos θ,
即a2-2a-1=0,所以a=1- 或a=1+ (舍去).
则sin θ+cos θ=sin θcos θ=1- .
