新教材人教B版数学必修第三册课件:7.2.4 诱导公式(一)(65张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.2.4 诱导公式(一)(65张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览









文档简介
课件65张PPT。7.2.4
诱导公式(一)1.诱导公式①
sin(α+k·2π)=sin α,?
cos(α+k·2π)=cos α,?
tan(α+k·2π)=tan α(k∈Z).?【思考】
根据三角函数的诱导公式①,终边相同的角的同名三角函数值有何关系?
提示:终边相同的角,其同名三角函数的值相等.
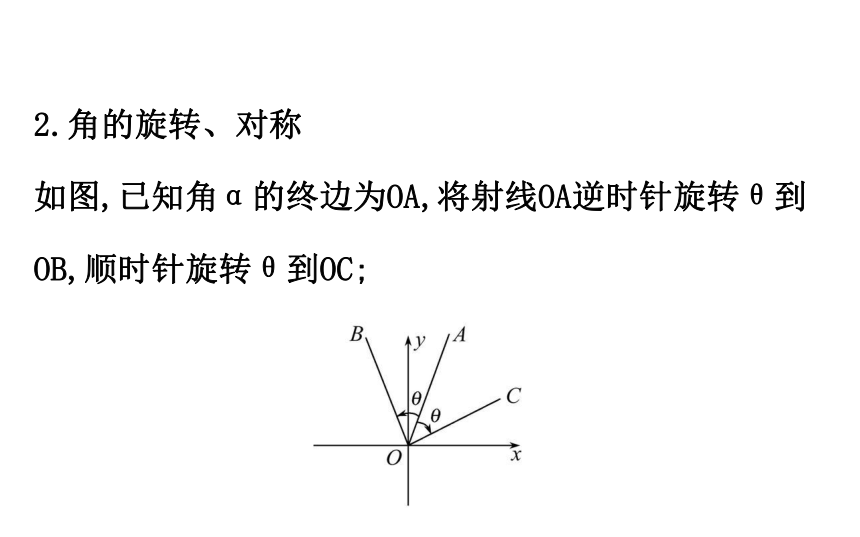
因为这些角的终边都是同一条射线,根据三角函数的定义可知这些角的三角函数值相等.2.角的旋转、对称
如图,已知角α的终边为OA,将射线OA逆时针旋转θ到OB,顺时针旋转θ到OC;则射线OB是角α+θ的终边,射线OC是角α-θ的终边,所以角α+θ的终边与角α-θ的终边关于角α的终边所在的直线对称.【思考】
角的正负与旋转方向之间的关系?
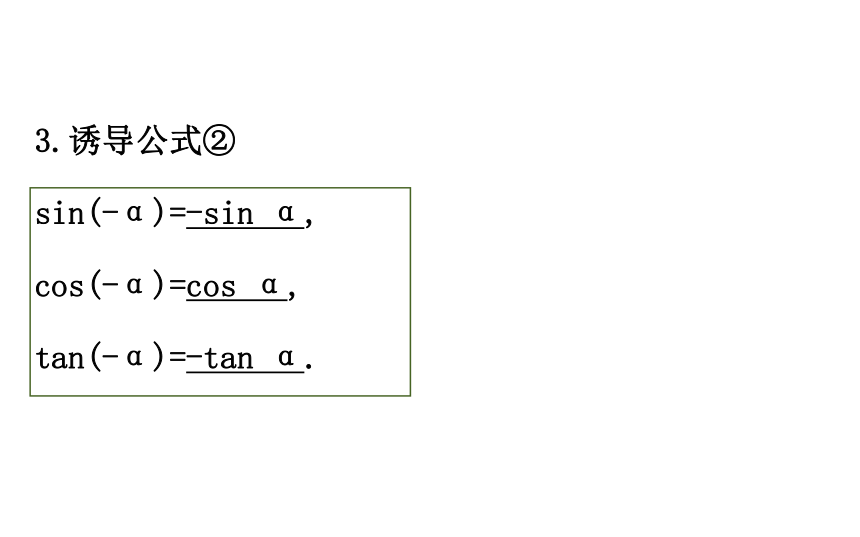
提示:将射线逆时针方向旋转得到正角,顺时针方向旋转得到负角.3.诱导公式②
sin(-α)=-sin α,?
cos(-α)=cos α,?
tan(-α)=-tan α.?【思考】
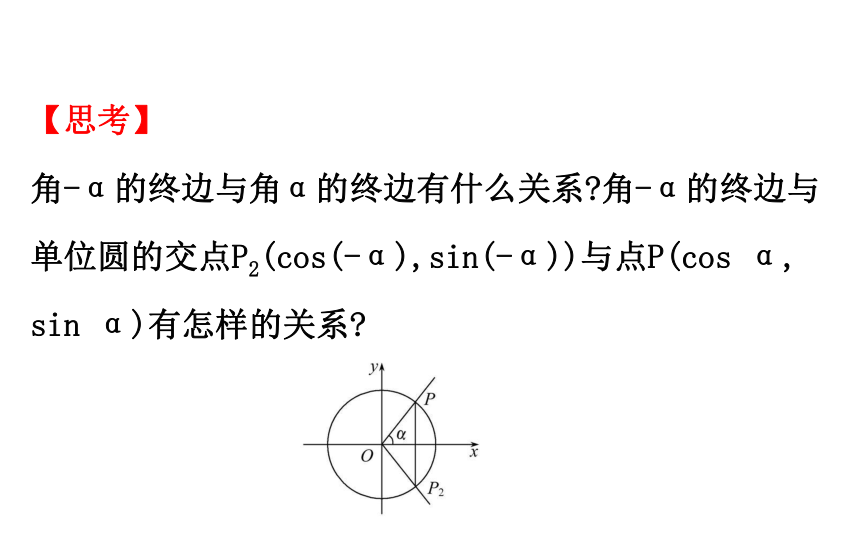
角-α的终边与角α的终边有什么关系?角-α的终边与
单位圆的交点P2(cos(-α),sin(-α))与点P(cos α,
sin α)有怎样的关系?提示:角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称.4.诱导公式③
sin(π-α)=sin α,?
cos(π-α)=-cos α,?
tan(π-α)=-tan α.?【思考】
角π-α的终边与角α的终边有什么关系?角π-α的终边与单位圆的交点P3(cos(π-α),sin(π-α))与点P(cos α,sin α)有怎样的关系?提示:角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称.5.诱导公式④
sin (π+α)=-sin α,?
cos (π+α)=-cos α,?
tan (π+α)=tan α.?【思考】
角π+α的终边与角α的终边有什么关系?角π+α的终边与单位圆的交点P4(cos(π+α),sin(π+α))与点P(cos α,sin α)呢?提示:角π+α的终边与角α的终边关于原点对称;P4与P也关于原点对称.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)诱导公式中角α是任意角. ( )
(2)sin(α-π)=sin α. ( )
(3) ( )提示:(1)×.正、余弦函数的诱导公式中,α为任意角,
但是正切函数的诱导公式中,α的取值必须使公式中
角的正切值有意义.
(2)×.sin(α-π)=sin[-(π-α)]=-sin(π-α)=
-sin α.
(3)√.cos 2.已知cos(π+θ)= ,则cos θ= ( )【解析】选B.cos(π+θ)=-cos θ= ,所以
cos θ=- .3.下列各式不正确的是 ( )
A.sin(α+180°)=-sin α
B.cos(-α+β)=-cos(α-β)
C.sin(-α-360°)=-sin α
D.cos(-α-β)=cos(α+β)【解析】选B.cos(-α+β)=cos[-(α-β)]=cos(α-β),故B项错误.4.填空:sin 600°=________.?【解析】sin 600°=sin(720°-120°)=sin(-120°)
=-sin 120°=-sin(180°-60°)=-sin 60°=- .
答案:- 类型一 给角求值问题
【典例】1.计算 的值是( )2.求下列各式的值:
(1)sin(-1 395°)cos 1 110°+
cos(-1 020°)sin 750°.
(2) 【思维·引】选择恰当的诱导公式,负角化正角,大角化小角,小角化锐角,然后利用特殊角的三角函数求值.【解析】1.选C.原式= 2.(1)原式=sin(-4×360°+45°)cos(3×360° +30°)+cos(-3×360°+60°)sin(2×360°+ 30°)=sin 45°cos 30°+cos 60°sin 30°(2)原式= 【内化·悟】
对于(-2π,2π)之间的角,怎样选择诱导公式化简?
提示:当一个角的绝对值不大时,一般选择“公式②、③、④”进行化简.【类题·通】
利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用诱导公式①或②来转化.
(2)“大化小”:用诱导公式①将角化为0°到360°间的角.(3)“小化锐”:用诱导公式③或④将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.【习练·破】
在平面直角坐标系xOy中,角α与角β均以Ox为始边,
它们的终边关于y轴对称,若sin α= ,则sin β =________.?【解析】因为角α与角β均以Ox为始边,
它们的终边关于y轴对称,
所以α+β=π+2kπ,k∈Z,所以β=π+2kπ-α.
sin β=sin(π+2kπ-α)=sin(π-α)=sin α= .
答案: 【加练·固】
求sin 585°cos 1 290°+cos(-30°)sin 210°+
tan 135°的值.【解析】sin 585°cos 1 290°+cos(-30°)sin 210°
+tan 135°
=sin(360°+225°)cos(3×360°+210°)+
cos 30°sin 210°+tan(180°-45°)
=sin 225°cos 210°+cos 30°sin 210°-tan 45°=sin(180°+45°)cos(180°+30°)+cos 30°·
sin(180°+ 30°)-tan 45°=sin 45°cos 30°
-cos 30°sin 30°-tan 45°类型二 给值(式)求值问题
【典例】1.已知sin =m,则sin
=( )
A.m B.-m C.±m D.不确定2.若cos 165°=a,则tan 195°= 世纪金榜导学
号( )【思维·引】1.分析两角 π-α,α+ π的特点能够发现,它们的和为2π,利用诱导公式即可求解.
2.165°=180°-15°,195°=180°+15°,分别用诱导公式即可求解.【解析】1.选B.因为
所以α+
所以 2.选B.cos 165°=cos(180°-15°)=-cos 15°=a,
故cos 15°=-a(a<0),得sin 15°= ,
tan 195°=tan(180°+15°)=tan 15°= 【内化·悟】
怎样找两个角之间的关系?
提示:解题时,我们一般把含有参变量的两个角相加或相减,寻找两个角之间的关系.对于不含参变量的角,我们一般直接观察两个角之间的关系,或者寻找给出角与特殊角之间的关系.【类题·通】
解决给值求值问题的策略
(1)解决给值求值问题,首先要仔细观察条件式与所求式之间的角、函数名称及有关运算之间的差异及联系.(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化. 【习练·破】
1.已知sin(π+α)= ,且α是第四象限角,则cos(α-2π)的值是 ( )【解析】选B.由sin(π+α)= ,得sin α=- ,
而cos(α-2π)=cos α,且α是第四象限角,
所以cos α= 2.已知 【解析】因为
所以 【加练·固】
已知sin β= ,cos(α+β)=-1,则sin(α+2β)的值为 ( )
A.1 B.-1 C. D.- 【解析】选D.因为cos(α+β)=-1,
所以α+β=π+2kπ,k∈Z,
所以sin(α+2β)=sin[(α+β)+β]=sin(π+β)
=-sin β=- .类型三 化简求值问题
【典例】1.计算:
=________.?2.已知tan(π+α)=m,求值:
世纪金榜导学号【思维·引】1.观察 的关系,分别用诱导公式化简.
2.先利用诱导公式求出tan α,再将所要求的式子化简后代入求值.【解析】1.原式=
答案:02.因为tan(π+α)=m,所以tan α=m,=-tan α=-m.【内化·悟】
1.对于多个非特殊角的题目怎样化简?提示:对于多个非特殊角的题目,我们要仔细观察角之
间的关系,例如典例1中 之间的关系,再
选择诱导公式化简.2.怎样解决复杂的三角函数式的化简、求值和证明问题?
提示:对于复杂的三角函数式,我们一般先利用诱导公式对每一项化简,再合在一起;注意,化简时一定要细心,尽量避免出现错误,特别是三角函数的符号错误.【类题·通】
三角函数式的化简方法
(1)利用诱导公式,将任意角的三角函数转化为锐角的
三角函数.
(2)常用“弦化切”法,即表达式中的弦函数通常化为
切函数.
(3)注意“1”的变式应用:如sin2α+cos2α=1=tan .【习练·破】
计算: 【解析】原式= 【加练·固】
求 (n∈Z)的值.【解析】①当n为奇数时,原式=
②当n为偶数时,原式=
诱导公式(一)1.诱导公式①
sin(α+k·2π)=sin α,?
cos(α+k·2π)=cos α,?
tan(α+k·2π)=tan α(k∈Z).?【思考】
根据三角函数的诱导公式①,终边相同的角的同名三角函数值有何关系?
提示:终边相同的角,其同名三角函数的值相等.
因为这些角的终边都是同一条射线,根据三角函数的定义可知这些角的三角函数值相等.2.角的旋转、对称
如图,已知角α的终边为OA,将射线OA逆时针旋转θ到OB,顺时针旋转θ到OC;则射线OB是角α+θ的终边,射线OC是角α-θ的终边,所以角α+θ的终边与角α-θ的终边关于角α的终边所在的直线对称.【思考】
角的正负与旋转方向之间的关系?
提示:将射线逆时针方向旋转得到正角,顺时针方向旋转得到负角.3.诱导公式②
sin(-α)=-sin α,?
cos(-α)=cos α,?
tan(-α)=-tan α.?【思考】
角-α的终边与角α的终边有什么关系?角-α的终边与
单位圆的交点P2(cos(-α),sin(-α))与点P(cos α,
sin α)有怎样的关系?提示:角-α的终边与角α的终边关于x轴对称,P2与P也关于x轴对称.4.诱导公式③
sin(π-α)=sin α,?
cos(π-α)=-cos α,?
tan(π-α)=-tan α.?【思考】
角π-α的终边与角α的终边有什么关系?角π-α的终边与单位圆的交点P3(cos(π-α),sin(π-α))与点P(cos α,sin α)有怎样的关系?提示:角π-α的终边与角α的终边关于y轴对称,P3与P也关于y轴对称.5.诱导公式④
sin (π+α)=-sin α,?
cos (π+α)=-cos α,?
tan (π+α)=tan α.?【思考】
角π+α的终边与角α的终边有什么关系?角π+α的终边与单位圆的交点P4(cos(π+α),sin(π+α))与点P(cos α,sin α)呢?提示:角π+α的终边与角α的终边关于原点对称;P4与P也关于原点对称.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)诱导公式中角α是任意角. ( )
(2)sin(α-π)=sin α. ( )
(3) ( )提示:(1)×.正、余弦函数的诱导公式中,α为任意角,
但是正切函数的诱导公式中,α的取值必须使公式中
角的正切值有意义.
(2)×.sin(α-π)=sin[-(π-α)]=-sin(π-α)=
-sin α.
(3)√.cos 2.已知cos(π+θ)= ,则cos θ= ( )【解析】选B.cos(π+θ)=-cos θ= ,所以
cos θ=- .3.下列各式不正确的是 ( )
A.sin(α+180°)=-sin α
B.cos(-α+β)=-cos(α-β)
C.sin(-α-360°)=-sin α
D.cos(-α-β)=cos(α+β)【解析】选B.cos(-α+β)=cos[-(α-β)]=cos(α-β),故B项错误.4.填空:sin 600°=________.?【解析】sin 600°=sin(720°-120°)=sin(-120°)
=-sin 120°=-sin(180°-60°)=-sin 60°=- .
答案:- 类型一 给角求值问题
【典例】1.计算 的值是( )2.求下列各式的值:
(1)sin(-1 395°)cos 1 110°+
cos(-1 020°)sin 750°.
(2) 【思维·引】选择恰当的诱导公式,负角化正角,大角化小角,小角化锐角,然后利用特殊角的三角函数求值.【解析】1.选C.原式= 2.(1)原式=sin(-4×360°+45°)cos(3×360° +30°)+cos(-3×360°+60°)sin(2×360°+ 30°)=sin 45°cos 30°+cos 60°sin 30°(2)原式= 【内化·悟】
对于(-2π,2π)之间的角,怎样选择诱导公式化简?
提示:当一个角的绝对值不大时,一般选择“公式②、③、④”进行化简.【类题·通】
利用诱导公式求任意角三角函数值的步骤
(1)“负化正”:用诱导公式①或②来转化.
(2)“大化小”:用诱导公式①将角化为0°到360°间的角.(3)“小化锐”:用诱导公式③或④将大于90°的角转化为锐角.
(4)“锐求值”:得到锐角的三角函数后求值.【习练·破】
在平面直角坐标系xOy中,角α与角β均以Ox为始边,
它们的终边关于y轴对称,若sin α= ,则sin β =________.?【解析】因为角α与角β均以Ox为始边,
它们的终边关于y轴对称,
所以α+β=π+2kπ,k∈Z,所以β=π+2kπ-α.
sin β=sin(π+2kπ-α)=sin(π-α)=sin α= .
答案: 【加练·固】
求sin 585°cos 1 290°+cos(-30°)sin 210°+
tan 135°的值.【解析】sin 585°cos 1 290°+cos(-30°)sin 210°
+tan 135°
=sin(360°+225°)cos(3×360°+210°)+
cos 30°sin 210°+tan(180°-45°)
=sin 225°cos 210°+cos 30°sin 210°-tan 45°=sin(180°+45°)cos(180°+30°)+cos 30°·
sin(180°+ 30°)-tan 45°=sin 45°cos 30°
-cos 30°sin 30°-tan 45°类型二 给值(式)求值问题
【典例】1.已知sin =m,则sin
=( )
A.m B.-m C.±m D.不确定2.若cos 165°=a,则tan 195°= 世纪金榜导学
号( )【思维·引】1.分析两角 π-α,α+ π的特点能够发现,它们的和为2π,利用诱导公式即可求解.
2.165°=180°-15°,195°=180°+15°,分别用诱导公式即可求解.【解析】1.选B.因为
所以α+
所以 2.选B.cos 165°=cos(180°-15°)=-cos 15°=a,
故cos 15°=-a(a<0),得sin 15°= ,
tan 195°=tan(180°+15°)=tan 15°= 【内化·悟】
怎样找两个角之间的关系?
提示:解题时,我们一般把含有参变量的两个角相加或相减,寻找两个角之间的关系.对于不含参变量的角,我们一般直接观察两个角之间的关系,或者寻找给出角与特殊角之间的关系.【类题·通】
解决给值求值问题的策略
(1)解决给值求值问题,首先要仔细观察条件式与所求式之间的角、函数名称及有关运算之间的差异及联系.(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化. 【习练·破】
1.已知sin(π+α)= ,且α是第四象限角,则cos(α-2π)的值是 ( )【解析】选B.由sin(π+α)= ,得sin α=- ,
而cos(α-2π)=cos α,且α是第四象限角,
所以cos α= 2.已知 【解析】因为
所以 【加练·固】
已知sin β= ,cos(α+β)=-1,则sin(α+2β)的值为 ( )
A.1 B.-1 C. D.- 【解析】选D.因为cos(α+β)=-1,
所以α+β=π+2kπ,k∈Z,
所以sin(α+2β)=sin[(α+β)+β]=sin(π+β)
=-sin β=- .类型三 化简求值问题
【典例】1.计算:
=________.?2.已知tan(π+α)=m,求值:
世纪金榜导学号【思维·引】1.观察 的关系,分别用诱导公式化简.
2.先利用诱导公式求出tan α,再将所要求的式子化简后代入求值.【解析】1.原式=
答案:02.因为tan(π+α)=m,所以tan α=m,=-tan α=-m.【内化·悟】
1.对于多个非特殊角的题目怎样化简?提示:对于多个非特殊角的题目,我们要仔细观察角之
间的关系,例如典例1中 之间的关系,再
选择诱导公式化简.2.怎样解决复杂的三角函数式的化简、求值和证明问题?
提示:对于复杂的三角函数式,我们一般先利用诱导公式对每一项化简,再合在一起;注意,化简时一定要细心,尽量避免出现错误,特别是三角函数的符号错误.【类题·通】
三角函数式的化简方法
(1)利用诱导公式,将任意角的三角函数转化为锐角的
三角函数.
(2)常用“弦化切”法,即表达式中的弦函数通常化为
切函数.
(3)注意“1”的变式应用:如sin2α+cos2α=1=tan .【习练·破】
计算: 【解析】原式= 【加练·固】
求 (n∈Z)的值.【解析】①当n为奇数时,原式=
②当n为偶数时,原式=
