新教材人教B版数学必修第三册课件:7.3.1 正弦函数的性质与图像(57张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.3.1 正弦函数的性质与图像(57张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览










文档简介
课件57张PPT。7.3 三角函数的性质与图像
7.3.1 正弦函数的性质与图像1.正弦函数的性质【思考】
(1)-2π是正弦函数的周期吗?
提示:是.2kπ(k∈Z,k≠0)都是它的周期.
(2)正弦函数的零点是点吗?若不是,是什么?
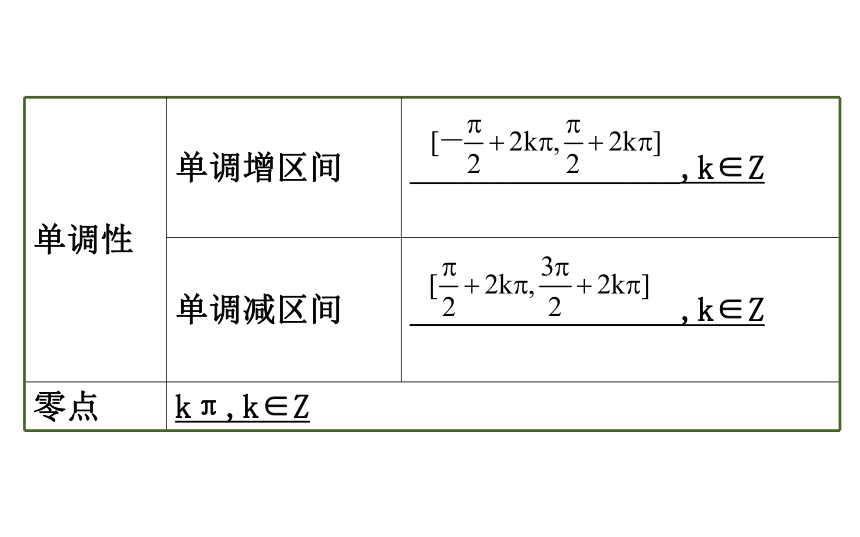
提示:不是,是实数kπ,k∈Z.2.函数的周期性
(1)周期:对于函数f(x),如果存在一个非零常数T,使得对定义域内的每一个x,都满足f(x+T)=f(x),那么就称函数f(x)为周期函数,非零常数T称为这个函数的周期.(2)最小正周期:对于一个周期函数f(x),如果在它的所有周期中存在一个最小的正数,那么这个最小的正数就称为f(x)的最小正周期.【思考】
对非零常数T,若存在x0,使f(x0+T)=f(x),那么T是函数的周期吗?为什么?
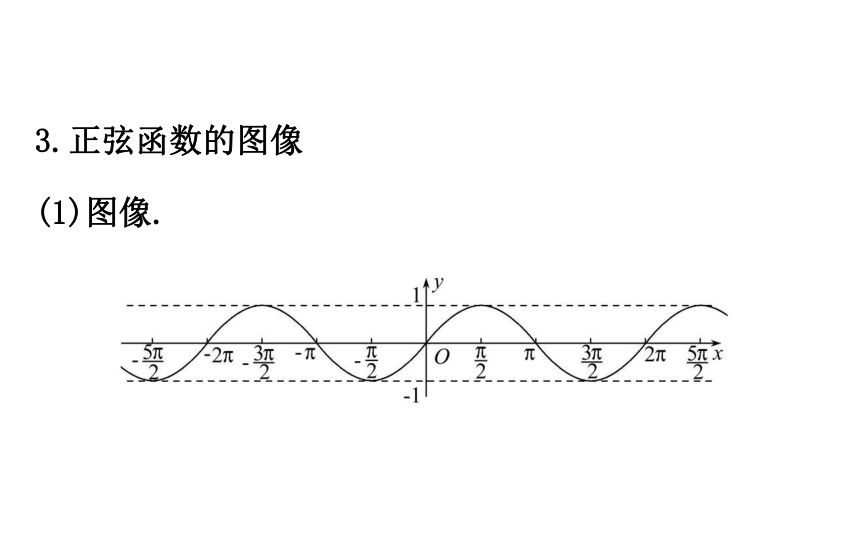
提示:不是,必须对定义域内的每一个值成立. 3.正弦函数的图像
(1)图像.(2)对称性:对称轴x=___+kπ,k∈Z,对称中心______,
k∈Z.
(3)五点: 【思考】
正弦函数的对称轴之间的距离有什么特点?对称中心呢?
提示:对称轴之间的距离相差了π的整数倍.对称中心之间的距离也相差了π的整数倍. 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)正弦函数在区间 上是递增的. ( )
(2)若存在一个常数T,使得对定义域内的每一个x,都有f(x+T)=f(x),则函数f(x)为周期函数. ( )
(3)函数f(x)=sin x-1的一个对称中心为(π,-1). ( )提示:(1)×.正弦函数在区间 上先递增,再递减.
(2)×.应为非零常数T.
(3)√.因为正弦函数的一个对称中心为(π,0),函数
f(x)=sin x-1即将正弦函数向下平移一个单位,故一
个对称中心为(π,-1).2.函数y=sin x是 ( )
A.增函数 B.减函数 C.偶函数 D.周期函数
【解析】选D.由正弦曲线y=sin x的图像,可得函数
y=sin x的增区间是 (k∈Z),减区间是
(k∈Z),函数是奇函数,且是周期为2π
的周期函数.3.若sin x=2m-1且x∈R,则m的取值范围是________.?
【解析】因为sin x=2m-1,x∈R,所以-1≤2m-1≤1,所
以0≤2m≤2,0≤m≤1,所以m的取值范围是[0,1].
答案: [0,1]类型一 正弦函数的性质及应用
角度1 比较大小
【典例】sin 1,sin 2,sin 3的大小关系是 ( )
A.sin 1C.sin 2调区间上,根据单调性比较大小.
【解析】选D.由sin 2=sin(π-2),sin 3=sin(π-3),
因为0<π-3<1<π-2< ,sin x在 上是增函数,
所以sin(π-3)故得sin 3在比较大小的过程中,常常用到核心素养中的逻辑推理,先利用诱导公式转化,再利用单调性比较大小.
将本例变为“sin 2,sin 3,sin 4”试比较其大小关系.【解析】由上题可知0=-sin(4-π)<0,所以sin 4【典例】1.(多选题)已知函数f(x)=2asin x+a+b的定
义域是 ,值域为[-5,-1],则a,b的值为( )
A.a=2,b=-7 B.a=-2,b=2
C.a=-2,b=1 D.a=1,b=-22.求函数f(x)=sin(π+x)-cos2x的最大值和最小值,并求出取得最大值和最小值时x的值.【思维·引】1.根据正弦函数的值域,分情况表示出最大值和最小值,通过解方程组求a,b.
2.利用诱导公式、同角三角函数的关系统一成正弦,还原求最值.【解析】1.选AC.因为f(x)=2asin x+a+b的定义域是
,所以0≤sin x≤1,当a<0时,由题意
所以 当a>0时,由题意 解得 2.f(x)=sin(π+x)-cos2x=-sin x-1+sin2x=sin2x-sin x
-1,令t=sin x,则y=t2-t-1= ,t∈[-1,1].
因为-1≤t≤1,所以 ≤y≤1,
所以ymax=1,此时sin x=-1,x= +2kπ,k∈Z;
所以ymin= ,此时sin x= ,x= +2kπ,k∈Z或
x= +2kπ,k∈Z.【类题·通】
1.关于正弦值大小比较
利用诱导公式将角化到正弦函数的单调区间内,通过单调性比较大小,如果不在一个单调区间,一是借助中间值,如0比较,二是利用正弦函数的对称轴转化比较.2.关于与正弦函数有关的最值
(1)一次式:如果是关于正弦函数的一次式,要根据一次项的系数正负确定最值;
(2)二次式:如果是关于正弦函数的二次式,则通过换元转化为一元二次函数配方求最值.【习练·破】
1.不求值,比较sin 与sin 的大小.【解析】sin =-sin =-sin ,sin
=-sin ,因为0< 且函数y=sin x,x∈
是增函数,所以sin-sin ,
即sin【解析】y=1-2sin2x+sin x,令sin x=t,
则-1≤t≤1,y=-2t2+t+1=-2 .
由二次函数y=-2t2+t+1的图像可知-2≤y≤ ,
即函数y=1-2sin2x+sin x的值域为 .【加练·固】
不求值比较sin 255°与sin 262°的大小.【解析】sin 255°=sin(180°+75°)=-sin 75°,
sin 262°=sin(180°+82°)=-sin 82°,
因为0°<75°<82°<90°,
且函数y=sin x,x∈ 是增函数,
所以sin 75°所以-sin 75°>-sin 82°,即sin 255°>sin 262°.类型二 五点法作正弦函数的图像
【典例】用五点法作函数y=-2sin x+1,x∈[0,2π]的图像. 世纪金榜导学号【思维·引】按照列表、描点、连线的步骤作图.
【解析】列表:描点作图:【内化·悟】
上述作图的过程中哪一步是最关键的?
提示:列表是作图的关键.【类题·通】
“五点法”作函数y=rsin x+l的图像
(1)列表:以正弦函数的五点为基础,列出函数y=rsin x+l的五点.
(2)描点:将函数y=rsin x+l的五点在坐标系中描出来.
(3)连线:利用平滑的曲线将点连接起来,注意不能用折线连接.【习练·破】
用“五点法”作出函数y=2-sin x,x∈[0,2π]的图像.【解析】列表如下:描点,用光滑曲线连起来,图像如图所示.【加练·固】
利用“五点法”作出函数y=sin ,x∈ 的
图像.【解析】列表如下:描点连线,如图所示.类型三 正弦函数性质、图像的应用
【典例】1.函数f(x)= -sin x在区间[0,2π]上的
零点个数为 ( )
A.1 B.2 C.3 D.4
2.求函数y= 的定义域、值域和零点.
世纪金榜导学号【思维·引】1.转化为函数图像的交点个数判断.
2.按照相关的概念列式,结合不等式、方程求解.【解析】1.选B.令f(x)= -sin x=0,即 =
sin x,如图所示.函数y= 与y=sin x在[0,2π]上有两个交点,
故函数f(x)= -sin x有两个零点.2.令 -2sin x≥0,即sinx≤ ,
解得 +2kπ≤x≤ +2kπ,k∈Z,
所以函数的定义域为 ,k∈Z.
因为-1≤sin x≤ ,所以0≤ -2sin x≤ +2,所以0≤ ,
故函数的值域为 .
令y= =0,
解得x= +2kπ或x= π+2kπ,k∈Z.【内化·悟】
本例1中,确定零点个数的方法是什么?
提示:数形结合.【类题·通】
关于正弦函数性质、图像的应用
(1)周期性的应用:正弦函数是周期函数,可以先研究其在一个周期内的性质,再推广到定义域内.(2)奇偶性的应用:先确定函数的奇偶性,只研究函数在[0,+∞)上的性质,再利用奇偶函数的性质推广到
(-∞,0]上.
(3)数形结合的应用:将问题转化为正弦函数与其他初等函数图像间的关系,利用图像解决问题.【习练·破】
1.(2020·福州高一检测)函数y= 的定义域
为( )【解析】选D.要使函数有意义,则2sin(π-2x)-1≥0,
即sin2x≥ ,则2kπ+ ≤2x≤2kπ+ ,k∈Z,
则kπ+ ≤x≤kπ+ ,k∈Z,
即函数的定义域为 2.函数f(x)=sin x- 的零点个数是 ( )
A.4 B.5 C.6 D.7【解析】选D.令f(x)=sin x- =0,即sin x= ,
令y1=sin x,y2= ,在同一坐标系内分别作出y1,y2的
图像如图.
由图像可知图像有7个交点,即函数有7个零点.【加练·固】
求方程sin x=lg x的解的个数.
【解析】建立平面直角坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π]的图像,再向右连续平移2π个单位,得到y=sin x的图像.描出点(1,0),(10,1),并用光滑曲线连接得到y=lg x
的图像,如图所示.
由图像可知方程sin x=lg x的解有3个.
7.3.1 正弦函数的性质与图像1.正弦函数的性质【思考】
(1)-2π是正弦函数的周期吗?
提示:是.2kπ(k∈Z,k≠0)都是它的周期.
(2)正弦函数的零点是点吗?若不是,是什么?
提示:不是,是实数kπ,k∈Z.2.函数的周期性
(1)周期:对于函数f(x),如果存在一个非零常数T,使得对定义域内的每一个x,都满足f(x+T)=f(x),那么就称函数f(x)为周期函数,非零常数T称为这个函数的周期.(2)最小正周期:对于一个周期函数f(x),如果在它的所有周期中存在一个最小的正数,那么这个最小的正数就称为f(x)的最小正周期.【思考】
对非零常数T,若存在x0,使f(x0+T)=f(x),那么T是函数的周期吗?为什么?
提示:不是,必须对定义域内的每一个值成立. 3.正弦函数的图像
(1)图像.(2)对称性:对称轴x=___+kπ,k∈Z,对称中心______,
k∈Z.
(3)五点: 【思考】
正弦函数的对称轴之间的距离有什么特点?对称中心呢?
提示:对称轴之间的距离相差了π的整数倍.对称中心之间的距离也相差了π的整数倍. 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)正弦函数在区间 上是递增的. ( )
(2)若存在一个常数T,使得对定义域内的每一个x,都有f(x+T)=f(x),则函数f(x)为周期函数. ( )
(3)函数f(x)=sin x-1的一个对称中心为(π,-1). ( )提示:(1)×.正弦函数在区间 上先递增,再递减.
(2)×.应为非零常数T.
(3)√.因为正弦函数的一个对称中心为(π,0),函数
f(x)=sin x-1即将正弦函数向下平移一个单位,故一
个对称中心为(π,-1).2.函数y=sin x是 ( )
A.增函数 B.减函数 C.偶函数 D.周期函数
【解析】选D.由正弦曲线y=sin x的图像,可得函数
y=sin x的增区间是 (k∈Z),减区间是
(k∈Z),函数是奇函数,且是周期为2π
的周期函数.3.若sin x=2m-1且x∈R,则m的取值范围是________.?
【解析】因为sin x=2m-1,x∈R,所以-1≤2m-1≤1,所
以0≤2m≤2,0≤m≤1,所以m的取值范围是[0,1].
答案: [0,1]类型一 正弦函数的性质及应用
角度1 比较大小
【典例】sin 1,sin 2,sin 3的大小关系是 ( )
A.sin 1
【解析】选D.由sin 2=sin(π-2),sin 3=sin(π-3),
因为0<π-3<1<π-2< ,sin x在 上是增函数,
所以sin(π-3)
将本例变为“sin 2,sin 3,sin 4”试比较其大小关系.【解析】由上题可知0
义域是 ,值域为[-5,-1],则a,b的值为( )
A.a=2,b=-7 B.a=-2,b=2
C.a=-2,b=1 D.a=1,b=-22.求函数f(x)=sin(π+x)-cos2x的最大值和最小值,并求出取得最大值和最小值时x的值.【思维·引】1.根据正弦函数的值域,分情况表示出最大值和最小值,通过解方程组求a,b.
2.利用诱导公式、同角三角函数的关系统一成正弦,还原求最值.【解析】1.选AC.因为f(x)=2asin x+a+b的定义域是
,所以0≤sin x≤1,当a<0时,由题意
所以 当a>0时,由题意 解得 2.f(x)=sin(π+x)-cos2x=-sin x-1+sin2x=sin2x-sin x
-1,令t=sin x,则y=t2-t-1= ,t∈[-1,1].
因为-1≤t≤1,所以 ≤y≤1,
所以ymax=1,此时sin x=-1,x= +2kπ,k∈Z;
所以ymin= ,此时sin x= ,x= +2kπ,k∈Z或
x= +2kπ,k∈Z.【类题·通】
1.关于正弦值大小比较
利用诱导公式将角化到正弦函数的单调区间内,通过单调性比较大小,如果不在一个单调区间,一是借助中间值,如0比较,二是利用正弦函数的对称轴转化比较.2.关于与正弦函数有关的最值
(1)一次式:如果是关于正弦函数的一次式,要根据一次项的系数正负确定最值;
(2)二次式:如果是关于正弦函数的二次式,则通过换元转化为一元二次函数配方求最值.【习练·破】
1.不求值,比较sin 与sin 的大小.【解析】sin =-sin =-sin ,sin
=-sin ,因为0< 且函数y=sin x,x∈
是增函数,所以sin
即sin
则-1≤t≤1,y=-2t2+t+1=-2 .
由二次函数y=-2t2+t+1的图像可知-2≤y≤ ,
即函数y=1-2sin2x+sin x的值域为 .【加练·固】
不求值比较sin 255°与sin 262°的大小.【解析】sin 255°=sin(180°+75°)=-sin 75°,
sin 262°=sin(180°+82°)=-sin 82°,
因为0°<75°<82°<90°,
且函数y=sin x,x∈ 是增函数,
所以sin 75°
【典例】用五点法作函数y=-2sin x+1,x∈[0,2π]的图像. 世纪金榜导学号【思维·引】按照列表、描点、连线的步骤作图.
【解析】列表:描点作图:【内化·悟】
上述作图的过程中哪一步是最关键的?
提示:列表是作图的关键.【类题·通】
“五点法”作函数y=rsin x+l的图像
(1)列表:以正弦函数的五点为基础,列出函数y=rsin x+l的五点.
(2)描点:将函数y=rsin x+l的五点在坐标系中描出来.
(3)连线:利用平滑的曲线将点连接起来,注意不能用折线连接.【习练·破】
用“五点法”作出函数y=2-sin x,x∈[0,2π]的图像.【解析】列表如下:描点,用光滑曲线连起来,图像如图所示.【加练·固】
利用“五点法”作出函数y=sin ,x∈ 的
图像.【解析】列表如下:描点连线,如图所示.类型三 正弦函数性质、图像的应用
【典例】1.函数f(x)= -sin x在区间[0,2π]上的
零点个数为 ( )
A.1 B.2 C.3 D.4
2.求函数y= 的定义域、值域和零点.
世纪金榜导学号【思维·引】1.转化为函数图像的交点个数判断.
2.按照相关的概念列式,结合不等式、方程求解.【解析】1.选B.令f(x)= -sin x=0,即 =
sin x,如图所示.函数y= 与y=sin x在[0,2π]上有两个交点,
故函数f(x)= -sin x有两个零点.2.令 -2sin x≥0,即sinx≤ ,
解得 +2kπ≤x≤ +2kπ,k∈Z,
所以函数的定义域为 ,k∈Z.
因为-1≤sin x≤ ,所以0≤ -2sin x≤ +2,所以0≤ ,
故函数的值域为 .
令y= =0,
解得x= +2kπ或x= π+2kπ,k∈Z.【内化·悟】
本例1中,确定零点个数的方法是什么?
提示:数形结合.【类题·通】
关于正弦函数性质、图像的应用
(1)周期性的应用:正弦函数是周期函数,可以先研究其在一个周期内的性质,再推广到定义域内.(2)奇偶性的应用:先确定函数的奇偶性,只研究函数在[0,+∞)上的性质,再利用奇偶函数的性质推广到
(-∞,0]上.
(3)数形结合的应用:将问题转化为正弦函数与其他初等函数图像间的关系,利用图像解决问题.【习练·破】
1.(2020·福州高一检测)函数y= 的定义域
为( )【解析】选D.要使函数有意义,则2sin(π-2x)-1≥0,
即sin2x≥ ,则2kπ+ ≤2x≤2kπ+ ,k∈Z,
则kπ+ ≤x≤kπ+ ,k∈Z,
即函数的定义域为 2.函数f(x)=sin x- 的零点个数是 ( )
A.4 B.5 C.6 D.7【解析】选D.令f(x)=sin x- =0,即sin x= ,
令y1=sin x,y2= ,在同一坐标系内分别作出y1,y2的
图像如图.
由图像可知图像有7个交点,即函数有7个零点.【加练·固】
求方程sin x=lg x的解的个数.
【解析】建立平面直角坐标系xOy,先用五点法画出函数y=sin x,x∈[0,2π]的图像,再向右连续平移2π个单位,得到y=sin x的图像.描出点(1,0),(10,1),并用光滑曲线连接得到y=lg x
的图像,如图所示.
由图像可知方程sin x=lg x的解有3个.
