新教材人教B版数学必修第三册课件:7.3.3 余弦函数的性质与图像(55张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.3.3 余弦函数的性质与图像(55张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 10:37:51 | ||
图片预览










文档简介
课件55张PPT。7.3.3 余弦函数的性质与图像1.余弦函数的定义
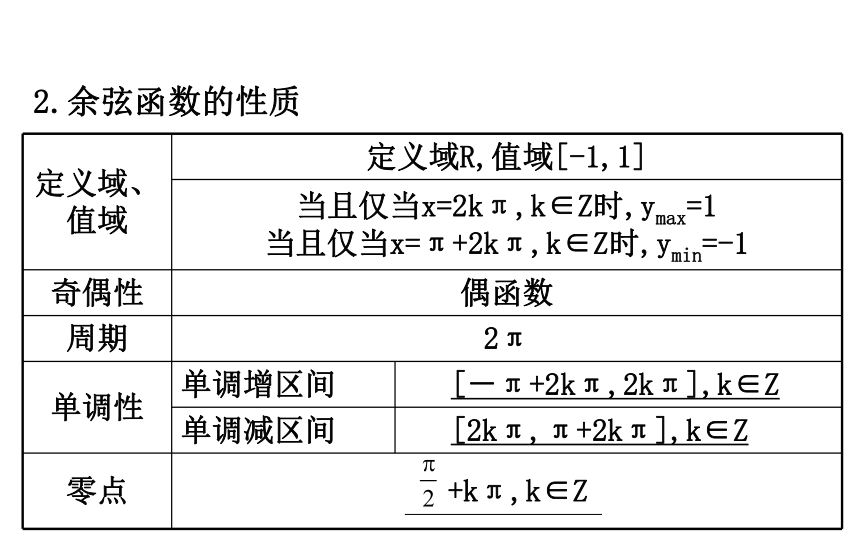
对于任意一个角x,都有唯一确定的余弦cos x与之对应,所以y=cos x称为余弦函数.?2.余弦函数的性质【思考】
(1)余弦函数的零点对应正弦函数的哪个性质?
提示:余弦函数的零点对应正弦函数的对称轴.(2)余弦型函数y=Acos(ωx+φ)的周期是多少?
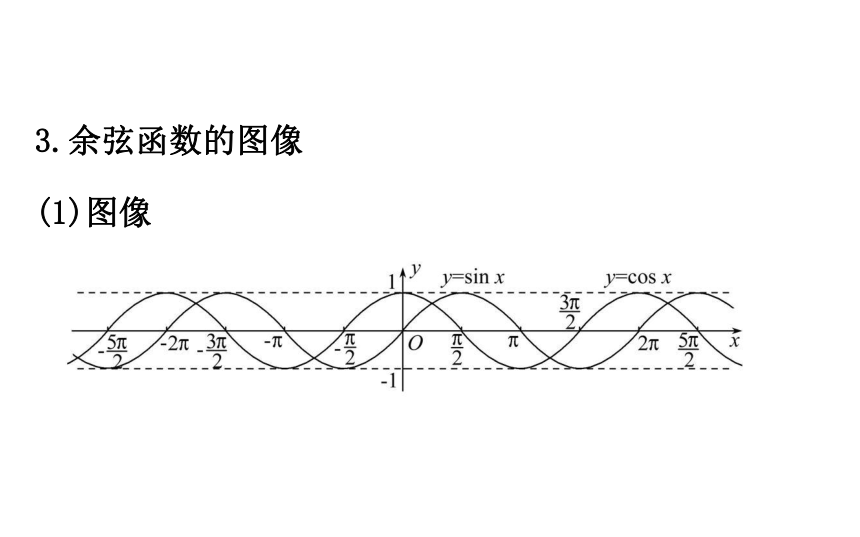
提示:T= .3.余弦函数的图像
(1)图像(2)对称性:对称轴x=kπ,对称中心 ,k∈Z.
(3)五点:(0,1), 【思考】
余弦函数的图像与正弦函数的图像有什么关系?
提示:余弦函数的图像可以看作正弦函数的图像向左
平移 个单位.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)余弦函数在区间 上是单调递增的.( )
(2)方程2cos x+3=0一定有解. ( )
(3)函数y=cos 的一条对称轴为 .( )提示:(1)×.余弦函数在 不具有单调性.
(2)×.方程变为cosx=- <-1,故无解.
(3)×.因为余弦函数的对称轴为x=kπ(k∈Z),函数
y=cos 可视为余弦函数向右平移 个单位得到,
因此y=cos ,关于x=kπ+ (k∈Z)对称.2.函数y=2cos 的最小正周期是 ( )
A. B. C.2π D.5π
【解析】选D.函数y=2cos 的最小正周期是
=5π.3.函数y=2cos x-3的值不可能是 ( )
A.0 B.-1 C.-3 D.-5
【解析】选A.因为-1≤cos x≤1,所以-2≤2cos x≤2,
则y=2cos x-3∈[-5,-1],所以函数y=2cos x-3的值不可能是0.类型一 余弦函数的单调性
【典例】1.(2020·葫芦岛高一检测)函数
f(x)=5cos 的一个单调递减区间是 ( )
2.(2020·济南高一检测)设a=cos ,b=sin ,
c=cos ,则 ( )
A.a>c>b B.c>b>a
C.c>a>b D.b>c>a【思维·引】1.先求出函数在定义域上的单调减区间,再验证.
2.利用诱导公式化到一个单调区间,再利用单调性比较.【解析】1.选B.f(x)=5cos ,
由2kπ≤3x+ ≤π+2kπ(k∈Z),
得 (k∈Z),
所以 是f(x)的一个单调递减区间.2.选A.
因为y=cos x在 上是减函数,
所以cos >cos >cos ,即a>c>b.【类题·通】
1.余弦型函数单调区间的求法
(1)如果x的系数为负,则利用诱导公式变为正.
(2)将ωx+φ看作整体,代入到余弦函数的单调区间解
出x的范围.
(3)若求具体的或一个范围内的单调区间,则给k赋值,
即可求出符合条件的单调区间.2.关于三角函数值比较大小
利用诱导公式,统一成正弦或余弦函数,统一化到一个单调区间内,利用单调性比较大小.【习练·破】
1.函数y= cos 的单调递增区间是________.?【解析】函数y= cos = cos ,
令-π+2kπ≤2x- ≤2kπ,k∈Z,
解得- +kπ≤x≤ +kπ,k∈Z,
所以函数y= cos 的单调递增区间是
,k∈Z.
答案: ,k∈Z2.(2020·上饶高一检测)将cos(-1),cos(-2),cos(-3)按大小顺序排列为________.(用“<”连接)?【解析】y=cos x在区间(-π,0)为增函数,
因为-π<-3<-2<-1<0,
所以cos(-3)答案:cos(-3)函数f(x)=cos 的最小正周期为________;若
x∈ ,则f(x)的单调递增区间为________.?【解析】函数f(x)=cos 的最小正周期为 ;
令2kπ+π≤3x+ ≤2kπ+2π,k∈Z,
求得 ,k∈Z,
可得函数的增区间为 ,k∈Z.
结合x∈ ,可得增区间为 .
答案: 类型二 余弦函数的奇偶性、对称性
【典例】1.(2020·天水高一检测)函数y=3cos
图像的一条对称轴可以是 ( )
A.x=- B.x=
C.x=- D.x= 2.(2020·济宁高一检测)函数y=3cos2x+4(x∈R)是( )
A.最小正周期为π的偶函数
B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数
D.最小正周期为2π的奇函数3.(2020·上海高一检测)已知φ是常数,如果函数
y=5cos(2x+φ)的图像关于点 中心对称,那么
|φ|的最小值为________. 世纪金榜导学号?【思维·引】1.令2x- =kπ,解出x后验证.
2.根据周期公式、偶函数的定义解题.
3.将 代入,令2× +φ= +kπ表示出φ.【解析】1.选B.根据函数y=3cos 的图像,
要求函数的对称轴方程,令2x- =kπ(k∈Z),
解得x= (k∈Z),
当k=1时,一条对称轴可以是x= .2.选A.函数f(x)=3cos2x+4,由于x∈R,
f(-x)=3cos(-2x)+4=f(x),故函数为偶函数,
最小正周期为T= =π.3.函数的图像关于点 中心对称,
所以f =5cos =5cos =0,
即 +φ=kπ+ (k∈Z),
解得φ=kπ- (k∈Z),当k=0时φ=- .
所以|φ|的最小值为 .
答案: 【内化·悟】
余弦函数的对称轴、对称中心分别是什么?
提示:对称轴x=kπ,k∈Z,对称中心 ,k∈Z.【类题·通】
关于余弦型函数y=Acos 的对称问题
(1)令ωx+φ=kπ,可解出对称轴,令ωx+φ= +kπ
可解出对称中心.(2)若已知x=α是对称轴,(α,0)是对称中心,则代入
α,ωα+φ=kπ或 +kπ,可求ω或φ.
(3)特别地,当φ=kπ,k∈Z时,函数为偶函数;
当φ= +kπ,k∈Z时,函数为奇函数.
【习练·破】
1.(2020·娄底高一检测)函数f(x)=3cos
图像的一个对称中心是 ( )
A. B.
C. D. 【解析】选B.对于函数f(x)=3cos 的图像,
令4x+ =kπ+ ,求得x= ,k=1时得函数
f(x)的一个对称中心是 .2.(2020·渭南高一检测)若函数f(x)=cos
(φ∈[0,2π])的图像关于y轴对称,则φ= ( )
A. B. C. D. 【解析】选B.因为函数f(x)=cos =
sin (φ∈[0,2π])的图像关于y轴对称,
所以 ,即φ= .【加练·固】
(2019·济南高一检测)若函数f(x)=cos 是奇函数,其中φ∈[0,π],则φ=________.?【解析】因为函数f(x)=cos 是奇函数,
可得f(x)=±sin ,φ∈[0,π],则φ= .
答案:
类型三 余弦函数的值域
角度1 定区间上求值域
【典例】求函数f(x)=cos x,x∈ 上的值域.
世纪金榜导学号
【思维·引】利用余弦函数的单调性求最值.【解析】由余弦函数的性质可知,f(x)=cos x在
上递增,在 上递减,
又因为f =- ,
所以函数的最大值为1,最小值为- ,
故值域为 .【素养·探】
在求余弦函数最值的过程中,常常用到核心素养中的
数学运算,借助单调性计算关键点的余弦值,从而确定
最大值、最小值.
将本例中的函数变为g(x)=cos ,区间不变,
求函数的值域.【解析】因为- ≤x≤ ,所以- ≤2x- ≤ ,
令t=2x- ,则y=cos t在区间 上递增,
在 上递减,所以y=cos t的最大值为1,
因为cos =cos故最小值为cos
故原函数的值域为 .角度2 与二次函数结合求最值
【典例】求函数y=sin2x+ cos x的值域.
世纪金榜导学号
【思维·引】利用同角三角函数关系转化为关于余弦的二次函数求最值.【解析】y=sin2x+ cos x=1-cos2x+ cos x
=-cos2x+ cos x+1=
令t=cos x,则y=- ,t∈ .
因为-1≤t≤1,所以当t= 时,ymax= ;
当t=-1时,ymin=- .
因此函数y=sin2x+ cos x的值域为 .【类题·通】
与余弦函数有关的最值问题
(1)求在R上的值域:当余弦在1或-1处取得最值,可直接代入验证,或分情况代入.(2)求定区间上的最值:可先计算t=ωx+φ的范围,根据y=cos t在所求出的范围内的单调性求最值.
(3)关于余弦的二次式求最值:可用换元法,配方法求最值.
【习练·破】
1.函数y=1-2cos x的最小值,最大值分别是 ( )
A.-1,3 B.-1,1
C.0,3 D.0,1
【解析】选A.因为-1≤cos x≤1,所以-1≤y≤3.2.求函数f(x)= cos ,x∈R在区间
上的最小值和最大值,并求出取得最值时x的值.【解析】因为x∈ ,则2x- ∈ ,
故cos ∈ ,
所以f(x)max= ,此时2x- =0,即x= ;
f(x)min=-1,此时2x- = ,即x= .【加练·固】
函数y=2cos -1的最小值是________,此时x=________.?【解析】当2x+ =π+2kπ,k∈Z,x= +kπ,
k∈Z时,ymin=-2-1=-3.
答案:-3 +kπ,k∈Z
对于任意一个角x,都有唯一确定的余弦cos x与之对应,所以y=cos x称为余弦函数.?2.余弦函数的性质【思考】
(1)余弦函数的零点对应正弦函数的哪个性质?
提示:余弦函数的零点对应正弦函数的对称轴.(2)余弦型函数y=Acos(ωx+φ)的周期是多少?
提示:T= .3.余弦函数的图像
(1)图像(2)对称性:对称轴x=kπ,对称中心 ,k∈Z.
(3)五点:(0,1), 【思考】
余弦函数的图像与正弦函数的图像有什么关系?
提示:余弦函数的图像可以看作正弦函数的图像向左
平移 个单位.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)余弦函数在区间 上是单调递增的.( )
(2)方程2cos x+3=0一定有解. ( )
(3)函数y=cos 的一条对称轴为 .( )提示:(1)×.余弦函数在 不具有单调性.
(2)×.方程变为cosx=- <-1,故无解.
(3)×.因为余弦函数的对称轴为x=kπ(k∈Z),函数
y=cos 可视为余弦函数向右平移 个单位得到,
因此y=cos ,关于x=kπ+ (k∈Z)对称.2.函数y=2cos 的最小正周期是 ( )
A. B. C.2π D.5π
【解析】选D.函数y=2cos 的最小正周期是
=5π.3.函数y=2cos x-3的值不可能是 ( )
A.0 B.-1 C.-3 D.-5
【解析】选A.因为-1≤cos x≤1,所以-2≤2cos x≤2,
则y=2cos x-3∈[-5,-1],所以函数y=2cos x-3的值不可能是0.类型一 余弦函数的单调性
【典例】1.(2020·葫芦岛高一检测)函数
f(x)=5cos 的一个单调递减区间是 ( )
2.(2020·济南高一检测)设a=cos ,b=sin ,
c=cos ,则 ( )
A.a>c>b B.c>b>a
C.c>a>b D.b>c>a【思维·引】1.先求出函数在定义域上的单调减区间,再验证.
2.利用诱导公式化到一个单调区间,再利用单调性比较.【解析】1.选B.f(x)=5cos ,
由2kπ≤3x+ ≤π+2kπ(k∈Z),
得 (k∈Z),
所以 是f(x)的一个单调递减区间.2.选A.
因为y=cos x在 上是减函数,
所以cos >cos >cos ,即a>c>b.【类题·通】
1.余弦型函数单调区间的求法
(1)如果x的系数为负,则利用诱导公式变为正.
(2)将ωx+φ看作整体,代入到余弦函数的单调区间解
出x的范围.
(3)若求具体的或一个范围内的单调区间,则给k赋值,
即可求出符合条件的单调区间.2.关于三角函数值比较大小
利用诱导公式,统一成正弦或余弦函数,统一化到一个单调区间内,利用单调性比较大小.【习练·破】
1.函数y= cos 的单调递增区间是________.?【解析】函数y= cos = cos ,
令-π+2kπ≤2x- ≤2kπ,k∈Z,
解得- +kπ≤x≤ +kπ,k∈Z,
所以函数y= cos 的单调递增区间是
,k∈Z.
答案: ,k∈Z2.(2020·上饶高一检测)将cos(-1),cos(-2),cos(-3)按大小顺序排列为________.(用“<”连接)?【解析】y=cos x在区间(-π,0)为增函数,
因为-π<-3<-2<-1<0,
所以cos(-3)
x∈ ,则f(x)的单调递增区间为________.?【解析】函数f(x)=cos 的最小正周期为 ;
令2kπ+π≤3x+ ≤2kπ+2π,k∈Z,
求得 ,k∈Z,
可得函数的增区间为 ,k∈Z.
结合x∈ ,可得增区间为 .
答案: 类型二 余弦函数的奇偶性、对称性
【典例】1.(2020·天水高一检测)函数y=3cos
图像的一条对称轴可以是 ( )
A.x=- B.x=
C.x=- D.x= 2.(2020·济宁高一检测)函数y=3cos2x+4(x∈R)是( )
A.最小正周期为π的偶函数
B.最小正周期为2π的偶函数
C.最小正周期为π的奇函数
D.最小正周期为2π的奇函数3.(2020·上海高一检测)已知φ是常数,如果函数
y=5cos(2x+φ)的图像关于点 中心对称,那么
|φ|的最小值为________. 世纪金榜导学号?【思维·引】1.令2x- =kπ,解出x后验证.
2.根据周期公式、偶函数的定义解题.
3.将 代入,令2× +φ= +kπ表示出φ.【解析】1.选B.根据函数y=3cos 的图像,
要求函数的对称轴方程,令2x- =kπ(k∈Z),
解得x= (k∈Z),
当k=1时,一条对称轴可以是x= .2.选A.函数f(x)=3cos2x+4,由于x∈R,
f(-x)=3cos(-2x)+4=f(x),故函数为偶函数,
最小正周期为T= =π.3.函数的图像关于点 中心对称,
所以f =5cos =5cos =0,
即 +φ=kπ+ (k∈Z),
解得φ=kπ- (k∈Z),当k=0时φ=- .
所以|φ|的最小值为 .
答案: 【内化·悟】
余弦函数的对称轴、对称中心分别是什么?
提示:对称轴x=kπ,k∈Z,对称中心 ,k∈Z.【类题·通】
关于余弦型函数y=Acos 的对称问题
(1)令ωx+φ=kπ,可解出对称轴,令ωx+φ= +kπ
可解出对称中心.(2)若已知x=α是对称轴,(α,0)是对称中心,则代入
α,ωα+φ=kπ或 +kπ,可求ω或φ.
(3)特别地,当φ=kπ,k∈Z时,函数为偶函数;
当φ= +kπ,k∈Z时,函数为奇函数.
【习练·破】
1.(2020·娄底高一检测)函数f(x)=3cos
图像的一个对称中心是 ( )
A. B.
C. D. 【解析】选B.对于函数f(x)=3cos 的图像,
令4x+ =kπ+ ,求得x= ,k=1时得函数
f(x)的一个对称中心是 .2.(2020·渭南高一检测)若函数f(x)=cos
(φ∈[0,2π])的图像关于y轴对称,则φ= ( )
A. B. C. D. 【解析】选B.因为函数f(x)=cos =
sin (φ∈[0,2π])的图像关于y轴对称,
所以 ,即φ= .【加练·固】
(2019·济南高一检测)若函数f(x)=cos 是奇函数,其中φ∈[0,π],则φ=________.?【解析】因为函数f(x)=cos 是奇函数,
可得f(x)=±sin ,φ∈[0,π],则φ= .
答案:
类型三 余弦函数的值域
角度1 定区间上求值域
【典例】求函数f(x)=cos x,x∈ 上的值域.
世纪金榜导学号
【思维·引】利用余弦函数的单调性求最值.【解析】由余弦函数的性质可知,f(x)=cos x在
上递增,在 上递减,
又因为f =- ,
所以函数的最大值为1,最小值为- ,
故值域为 .【素养·探】
在求余弦函数最值的过程中,常常用到核心素养中的
数学运算,借助单调性计算关键点的余弦值,从而确定
最大值、最小值.
将本例中的函数变为g(x)=cos ,区间不变,
求函数的值域.【解析】因为- ≤x≤ ,所以- ≤2x- ≤ ,
令t=2x- ,则y=cos t在区间 上递增,
在 上递减,所以y=cos t的最大值为1,
因为cos =cos
故原函数的值域为 .角度2 与二次函数结合求最值
【典例】求函数y=sin2x+ cos x的值域.
世纪金榜导学号
【思维·引】利用同角三角函数关系转化为关于余弦的二次函数求最值.【解析】y=sin2x+ cos x=1-cos2x+ cos x
=-cos2x+ cos x+1=
令t=cos x,则y=- ,t∈ .
因为-1≤t≤1,所以当t= 时,ymax= ;
当t=-1时,ymin=- .
因此函数y=sin2x+ cos x的值域为 .【类题·通】
与余弦函数有关的最值问题
(1)求在R上的值域:当余弦在1或-1处取得最值,可直接代入验证,或分情况代入.(2)求定区间上的最值:可先计算t=ωx+φ的范围,根据y=cos t在所求出的范围内的单调性求最值.
(3)关于余弦的二次式求最值:可用换元法,配方法求最值.
【习练·破】
1.函数y=1-2cos x的最小值,最大值分别是 ( )
A.-1,3 B.-1,1
C.0,3 D.0,1
【解析】选A.因为-1≤cos x≤1,所以-1≤y≤3.2.求函数f(x)= cos ,x∈R在区间
上的最小值和最大值,并求出取得最值时x的值.【解析】因为x∈ ,则2x- ∈ ,
故cos ∈ ,
所以f(x)max= ,此时2x- =0,即x= ;
f(x)min=-1,此时2x- = ,即x= .【加练·固】
函数y=2cos -1的最小值是________,此时x=________.?【解析】当2x+ =π+2kπ,k∈Z,x= +kπ,
k∈Z时,ymin=-2-1=-3.
答案:-3 +kπ,k∈Z
