新教材人教B版数学必修第三册课件:7.3.5 已知三角函数值求角(44张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:7.3.5 已知三角函数值求角(44张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览










文档简介
课件44张PPT。7.3.5 已知三角函数值求角类型一 利用正弦值求角、解不等式
角度1 已知正弦值求角
【典例】已知sin x=- ,求x.
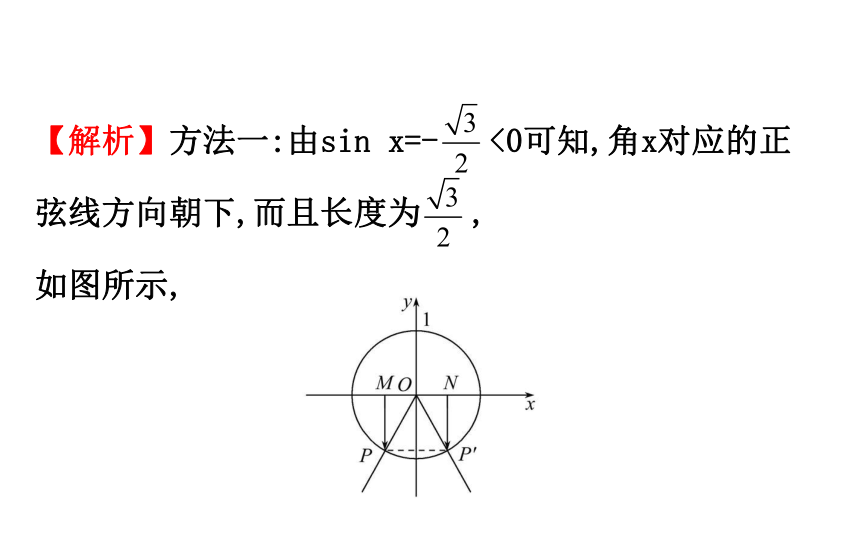
【思维·引】利用三角函数线或正弦函数的图像解题.【解析】方法一:由sin x=- <0可知,角x对应的正
弦线方向朝下,而且长度为 ,
如图所示,可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin =- ,
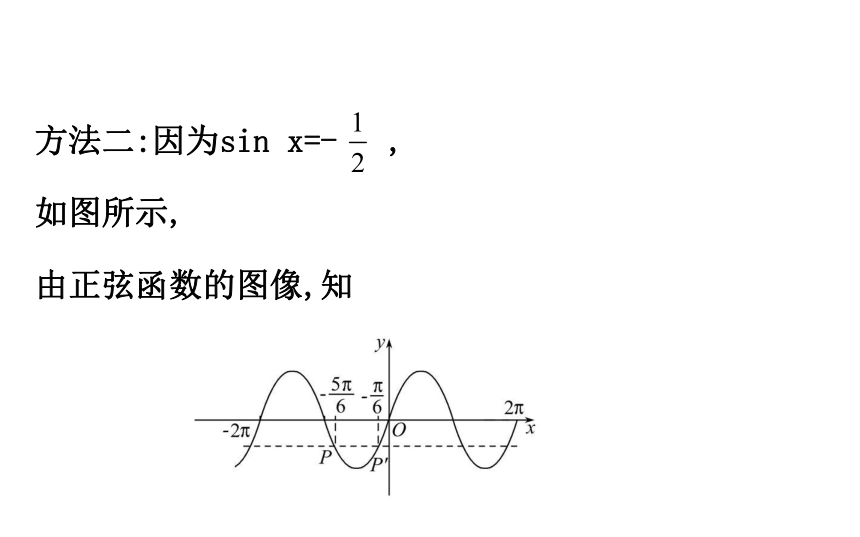
所以x= +2kπ或x= +2kπ,k∈Z.方法二:因为sin x=- ,
如图所示,
由正弦函数的图像,知
在 内,sin =sin =- ,
所以x= +2kπ或x= +2kπ,k∈Z.【素养·探】
在已知正弦值求角的过程中,常常用到核心素养中的直观想象,借助三角函数线或图像求角.
将本例改为sin x= ,试求x.【解析】由sinx= >0可知,角x对应的正弦线方向朝
上,而且长度为 ,如图所示,
可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin = ,
所以x= +2kπ或x= +2kπ,k∈Z.角度2 利用正弦值解不等式
【典例】求不等式sin x<- 的解集.
【思维·引】利用三角函数线、图像结合周期性求解集.【解析】方法一:由sin x=- <0可知,角x对应的正
弦线方向朝下,而且长度为 ,如图所示,
可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin =- ,
所以x=- +2kπ或x=- +2kπ,k∈Z.
如果x终边在∠POP′中,则有sin x<- ,所以- +2kπ所以不等式的解集为
方法二:因为sin x=- ,
如图所示,
由正弦函数的图像,知在 内,sin =sin =- ,
所以x=- +2kπ或x=- +2kπ,k∈Z,
所以- +2kπ所以不等式的解集为
【类题·通】
1.利用正弦值求角
利用正弦线、正弦函数的图像求出一个周期(常用
)内的角,再表示出定义域上的
所有取值,即加周期的k(k∈Z)倍.2.利用正弦值解不等式
先求出相等时的x值,再根据单位圆、图像确定x的范围.【习练·破】
求不等式sin x>- 的解集.【解析】当sin x=- 时,
x= +2kπ或x=- +2kπ,k∈Z,
所以- +2kπ所以不等式的解集为 类型二 利用余弦值求角、解不等式
【典例】1.已知cos ,求x.
2.求不等式cos 的解集.
世纪金榜导学号【思维·引】1.利用余弦线、图像求值.
2.先求出相等时的x值,再写出满足不等式的x的范围.【解析】1.由cos >0,知角2x- 对应的
余弦线方向向右,且长度为 ,
如图所示,可知角2x- 的终边可能是OP,也可能是OP′.
又因为cos =cos(- )= ,
所以2x- =- +2kπ或2x- = +2kπ,k∈Z.
所以x= +kπ或x= +kπ,k∈Z.2.如图所示,
在 上,
x+ =- 或 x+ = 时,cos
所以 x+ =- +2kπ或 x+ = +2kπ,
k∈Z时,cos 令- +2kπ< x+ < +2kπ,k∈Z,
解得- +4kπ所以不等式的解集为
【内化·悟】
已知余弦值怎样作余弦线?
提示:余弦线在x轴上,余弦大于0时从原点出发向右截取,余弦小于0时从原点出发向左截取.【类题·通】
利用余弦值求角、解不等式
将ωx+φ看作整体,先求出[0,2π]或[-π,π]上的角,再通过周期推广到整个定义域内,最后解出x的值或范围.【习练·破】
1.若cos(π-x)= ,x∈(-π,π),则x的值等于( )
A. B.±
C.± D.± 【解析】选C.由cos(π-x)=-cos x= 得,
cos x=- .
又因为x∈(-π,π),所以x在第二或第三象限,
所以x=± .2.求不等式2cos <0的解集.
【解析】不等式变为cos < ,
则 +2kπ<2x+ < +2kπ,k∈Z,
解得 +kπ所以不等式的解集为 类型三 利用正切值求角、解不等式
【典例】1.方程tan 在区间[0,2π)上的解的个数是 ( )
A.2 B.3 C.4 D.52.已知f(x)=tan ,求使f(x)≤- 成立的x的集合. 世纪金榜导学号
【思维·引】1.利用正切线或图像求值.
2.先求x的范围,再根据周期写解集.【解析】1.选C.
方法一:令t=2x+ ,作出函数y=tan t的图像如图:
令2x+ = +kπ,k∈Z,所以x= ,k∈Z.
又由0≤ <2π,所以k=0,1,2,3.
故在区间[0,2π)上有4个解.方法二:由tan >0,设t=2x+ ,
所以角2x+ 对应的正切线方向朝上,而且长度为 ,
如图所示,可知2x+ 的终边可能是OT,也可能是OT′, 因为tan =tan ,
所以2x+ = +kπ,k∈Z,所以x= ,k∈Z.
又由0≤ <2π,所以k=0,1,2,3.
故在区间[0,2π)上有4个解.
2.方法一:令t=3x- ,作出函数y=tan t的图像如图,
则- +kπ即- +kπ<3x- ≤- +kπ,k∈Z,解得- 所以不等式tan 的解集为
,k∈Z.方法二:因为tan <0,令t=3x- ,
所以角3x- 对应的正切线方向朝下,而且长度为 ,
如图所示,
可知3x- 的终边可能是OT,也可能是OT′,
因为tan =tan ,
即- +kπ<3x- ≤- +kπ,k∈Z,
解得- +所以不等式tan 的解集为 ,
k∈Z.【内化·悟】
怎样作当tan x=a时角x的正切线?
提示:过点A(1,0),作x轴的垂线,当a>0时,向上截取AT=a;当a<0时,向下截取AT=-a.【类题·通】
已知正切值求角、解不等式
(1)将ωx+φ看作一个整体,先根据正切线、图像求出
一个周期内的值或范围,一般选取 ,再推广到
定义域上,正切加kπ,区别于正、余弦加2kπ.
(2)最后代入ωx+φ求值或求范围.【习练·破】
当0【解析】由正切函数的图像知,当0若tan x<-1,则 答案: 【加练·固】
(2020·兰州高一检测)函数y=1+tan 在区间
(-π,π)内的零点个数为________.?【解析】函数y=1+tan ,
令1+tan =0,得tan =-1,
所以2x- =kπ- ,k∈Z;解得x= ,k∈Z;
当k=-1时,x=- ;当k=0时,x=- ;
当k=1时,x= ;当k=2时,x= ;所以y在区间(-π,π)内的零点有4个.
答案:4
角度1 已知正弦值求角
【典例】已知sin x=- ,求x.
【思维·引】利用三角函数线或正弦函数的图像解题.【解析】方法一:由sin x=- <0可知,角x对应的正
弦线方向朝下,而且长度为 ,
如图所示,可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin =- ,
所以x= +2kπ或x= +2kπ,k∈Z.方法二:因为sin x=- ,
如图所示,
由正弦函数的图像,知
在 内,sin =sin =- ,
所以x= +2kπ或x= +2kπ,k∈Z.【素养·探】
在已知正弦值求角的过程中,常常用到核心素养中的直观想象,借助三角函数线或图像求角.
将本例改为sin x= ,试求x.【解析】由sinx= >0可知,角x对应的正弦线方向朝
上,而且长度为 ,如图所示,
可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin = ,
所以x= +2kπ或x= +2kπ,k∈Z.角度2 利用正弦值解不等式
【典例】求不等式sin x<- 的解集.
【思维·引】利用三角函数线、图像结合周期性求解集.【解析】方法一:由sin x=- <0可知,角x对应的正
弦线方向朝下,而且长度为 ,如图所示,
可知角x的终边可能是OP,也可能是OP′.
又因为sin =sin =- ,
所以x=- +2kπ或x=- +2kπ,k∈Z.
如果x终边在∠POP′中,则有sin x<- ,所以- +2kπ
方法二:因为sin x=- ,
如图所示,
由正弦函数的图像,知在 内,sin =sin =- ,
所以x=- +2kπ或x=- +2kπ,k∈Z,
所以- +2kπ
【类题·通】
1.利用正弦值求角
利用正弦线、正弦函数的图像求出一个周期(常用
)内的角,再表示出定义域上的
所有取值,即加周期的k(k∈Z)倍.2.利用正弦值解不等式
先求出相等时的x值,再根据单位圆、图像确定x的范围.【习练·破】
求不等式sin x>- 的解集.【解析】当sin x=- 时,
x= +2kπ或x=- +2kπ,k∈Z,
所以- +2kπ
【典例】1.已知cos ,求x.
2.求不等式cos 的解集.
世纪金榜导学号【思维·引】1.利用余弦线、图像求值.
2.先求出相等时的x值,再写出满足不等式的x的范围.【解析】1.由cos >0,知角2x- 对应的
余弦线方向向右,且长度为 ,
如图所示,可知角2x- 的终边可能是OP,也可能是OP′.
又因为cos =cos(- )= ,
所以2x- =- +2kπ或2x- = +2kπ,k∈Z.
所以x= +kπ或x= +kπ,k∈Z.2.如图所示,
在 上,
x+ =- 或 x+ = 时,cos
所以 x+ =- +2kπ或 x+ = +2kπ,
k∈Z时,cos 令- +2kπ< x+ < +2kπ,k∈Z,
解得- +4kπ
【内化·悟】
已知余弦值怎样作余弦线?
提示:余弦线在x轴上,余弦大于0时从原点出发向右截取,余弦小于0时从原点出发向左截取.【类题·通】
利用余弦值求角、解不等式
将ωx+φ看作整体,先求出[0,2π]或[-π,π]上的角,再通过周期推广到整个定义域内,最后解出x的值或范围.【习练·破】
1.若cos(π-x)= ,x∈(-π,π),则x的值等于( )
A. B.±
C.± D.± 【解析】选C.由cos(π-x)=-cos x= 得,
cos x=- .
又因为x∈(-π,π),所以x在第二或第三象限,
所以x=± .2.求不等式2cos <0的解集.
【解析】不等式变为cos < ,
则 +2kπ<2x+ < +2kπ,k∈Z,
解得 +kπ
【典例】1.方程tan 在区间[0,2π)上的解的个数是 ( )
A.2 B.3 C.4 D.52.已知f(x)=tan ,求使f(x)≤- 成立的x的集合. 世纪金榜导学号
【思维·引】1.利用正切线或图像求值.
2.先求x的范围,再根据周期写解集.【解析】1.选C.
方法一:令t=2x+ ,作出函数y=tan t的图像如图:
令2x+ = +kπ,k∈Z,所以x= ,k∈Z.
又由0≤ <2π,所以k=0,1,2,3.
故在区间[0,2π)上有4个解.方法二:由tan >0,设t=2x+ ,
所以角2x+ 对应的正切线方向朝上,而且长度为 ,
如图所示,可知2x+ 的终边可能是OT,也可能是OT′, 因为tan =tan ,
所以2x+ = +kπ,k∈Z,所以x= ,k∈Z.
又由0≤ <2π,所以k=0,1,2,3.
故在区间[0,2π)上有4个解.
2.方法一:令t=3x- ,作出函数y=tan t的图像如图,
则- +kπ
,k∈Z.方法二:因为tan <0,令t=3x- ,
所以角3x- 对应的正切线方向朝下,而且长度为 ,
如图所示,
可知3x- 的终边可能是OT,也可能是OT′,
因为tan =tan ,
即- +kπ<3x- ≤- +kπ,k∈Z,
解得- +
k∈Z.【内化·悟】
怎样作当tan x=a时角x的正切线?
提示:过点A(1,0),作x轴的垂线,当a>0时,向上截取AT=a;当a<0时,向下截取AT=-a.【类题·通】
已知正切值求角、解不等式
(1)将ωx+φ看作一个整体,先根据正切线、图像求出
一个周期内的值或范围,一般选取 ,再推广到
定义域上,正切加kπ,区别于正、余弦加2kπ.
(2)最后代入ωx+φ求值或求范围.【习练·破】
当0
(2020·兰州高一检测)函数y=1+tan 在区间
(-π,π)内的零点个数为________.?【解析】函数y=1+tan ,
令1+tan =0,得tan =-1,
所以2x- =kπ- ,k∈Z;解得x= ,k∈Z;
当k=-1时,x=- ;当k=0时,x=- ;
当k=1时,x= ;当k=2时,x= ;所以y在区间(-π,π)内的零点有4个.
答案:4
