新教材人教B版数学必修第三册课件:8.1.2 向量数量积的运算律(61张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:8.1.2 向量数量积的运算律(61张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览







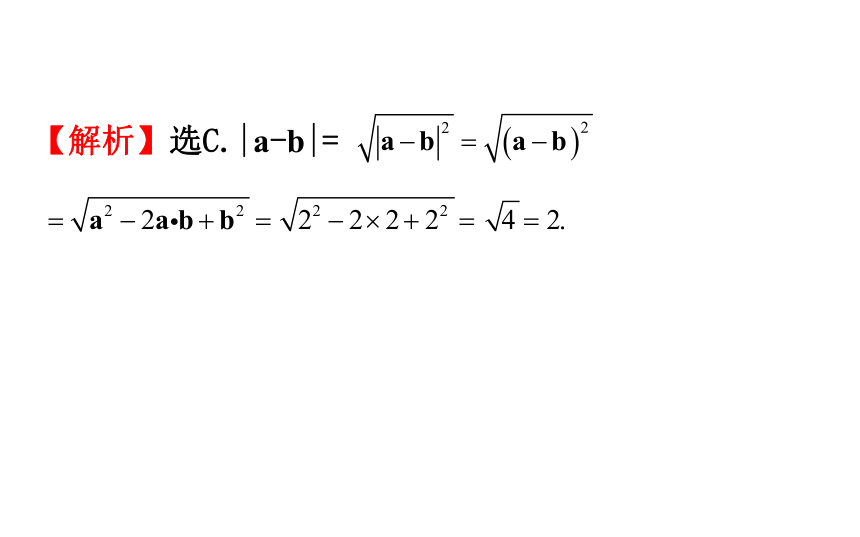




文档简介
课件61张PPT。8.1.2 向量数量积的运算律向量数量积的运算律
(1)a·b=b·a(交换律).
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c(分配律).【思考】
“若a·b=a·c,则b=c”成立吗?请说明原因.
提示:不成立.如a⊥b,a⊥c时,a·b=a·c,但b与c不一定相等.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)(a·b)·c=a·(b·c). ( )
(2)(a·b)2=a2·b2. ( )
(3)a·[b(a·c)-c(a·b)]=0. ( )提示:(1)×.向量(a·b)·c与c共线,a·(b·c)与a共线,故不正确.
(2)×.(a·b)2=(|a||b|·cos θ)2=a2b2cos2θ.
(3)√.a·[b(a·c)-c(a·b)]=(a·b)(a·c)-(a·c)(a·b)=0.2.已知|a|=|b|=2,a·b=2,则|a-b|= ( )
A.1 B. C.2 D. 或2【解析】选C.|a-b|=
3.若向量a,b满足|a|=|b|=1,且a·(a-b)= ,则向量
a与b的夹角为 ( )
A. B. C. D. 【解析】选B.因为a·(a-b)=a2-a·b= ,
所以1-1×1×cos= ,
所以cos= ,
因为0≤≤π,所以θ= .4.已知菱形ABCD的边长为a,∠ABC=60°,则 ·
等于 ( )
A.- a2 B.- a2 C. a2 D. a2【解析】选D.如图所示,由题意,得BC=a, CD=a,∠BCD=120°.
所以
=a·a·cos 60°+a2= a2.类型一 向量数量积的运算律的应用
【典例】1.(2018·全国卷Ⅱ)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)= ( )
A.4 B.3 C.2 D.02.(2020·长春高二检测)已知向量|a+b|=|a-b|,且|a|=|b|=2,则|2a-b|= ( )
A.2 B.2 C.2 D. 3.(2020·马鞍山高一检测) 如图,四边形ABCD是边长
为2的菱形,∠BAD=60°,E,F分别为BC,CD的中点,
则 · = ( )
A. B.- C. D.- 【思维·引】
1.利用向量数量积的定义与运算律计算.
2.先利用|a+b|=|a-b|得出a·b=0,再利用a2=|a|2和
向量数量积运算律计算.
3.先分别用基向量 表示 ,再利用向量
数量积的定义与运算律计算.【解析】1.选B. a·(2a-b)=2a2-a·b=2-(-1)=3.
2.选C.因为向量|a+b|=|a-b|,
所以a·b=0,又|a|=|b|=2,
所以|2a-b|= =2 .3.选D. 因为菱形ABCD的边长为2,∠BAD=60°,
所以 =2×2×cos 60°=2,
又因为
所以 【内化·悟】
1.形如“a·(2a-b)”的计算将如何进行?
提示:类比单项式乘以多项式的计算方法进行.2.根据模长公式,求向量的模的问题应首先做怎样的转化?
提示:求模问题一般转化为求模的平方.3.如何解决几何图形中向量数量积的计算?
提示:一般选择已知长度与夹角的向量作基底,用基底表示要求数量积的向量,再计算.【类题·通】
向量数量积运算中的常用结论
(1)a2=|a|2.
(2)(xa+yb)·(mc+nd)=xma·c+xna·d+ymb·c+ynb·d,其中x,y,m,n∈R,类似于多项式的乘法法则.(3)(a+b)2=a2+2a·b+b2.
(4)(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c.【习练·破】
1.已知向量a与b的夹角为120°,且|a|=4,|b|=2,则(2a-b)·(a+3b)=________.?【解析】(2a-b)·(a+3b)=2a2+6a·b-a·b-3b2
=2|a|2+5a·b-3|b|2
=2×16+5×4×2×cos 120°-3×4=0.
答案:02.(2019·临沂高一检测)已知向量a,b满足|b|=5, |2a+b|=5 ,|a-b|=5 ,则|a|=________.?【解析】由已知有
将b2=|b|2=25代入方程组,解得|a|= .
答案: 【加练·固】
(2020·烟台高一检测)在△ABC中,已知| + |=
| - |,AB=1,AC=3,M,N分别为BC的三等分点(M靠
近B,N靠近C),则 · = ( )
A. B. C. D. 【解析】选B.因为| + |=| - |,
所以∠BAC=90°.又M,N分别为BC的三等分点, 类型二 向量的夹角和垂直问题
角度1 求向量的夹角
【典例】(2019·全国卷Ⅰ)已知非零向量a,b满足
|a|=2|b|,且(a-b)⊥b,则a与b的夹角为 ( )
A. B. C. D. 【思维·引】利用夹角公式计算.
【解析】选B.设夹角为θ,因为(a-b)⊥b,
所以(a-b)·b=a·b-b2=0,所以a·b=b2,
所以cos θ= ,又θ∈[0,π],
所以a与b的夹角为 ,故选B.【素养·探】
解决向量的夹角与垂直问题时,常常需要结合图形分析问题,突出体现了数学抽象和直观想象的核心素养.
若将本例条件改为“|a|=3|b|=|a+2b|”,试求a与b夹角的余弦值.【解析】设a与b夹角为θ,因为|a|=3|b|,
所以|a|2=9|b|2.
又|a|=|a+2b|,
所以|a|2=|a|2+4|b|2+4a·b
=|a|2+4|b|2+4|a|·|b|·cos θ=13|b|2+12|b|2cos θ,
即9|b|2=13|b|2+12|b|2cos θ,
故有cos θ=- .
角度2 向量垂直的应用
【典例】 (2019·枣庄高一检测)已知非零向量m,n的
夹角为θ,且满足4|m|=3|n|,cos θ= .
若n⊥(t m+n),则实数t的值为世纪金榜导学号( )
A.4 B.-4 C. D.- 【思维·引】利用向量垂直的充要条件求参数.
【解析】选B.由4|m|=3|n|,
可设|m|=3k,|n|=4k(k>0),
又n⊥(t m+n),所以n·(t m+n)=n·t m+n·n
=t|m|·|n|cos θ+|n|2
=t×3k×4k× +(4k)2
=4tk2+16k2=0.
所以t=-4.【类题·通】
1.求向量夹角问题一般有两种思路
(1)数量积a·b与模积|a||b|好求解,直接用变形公式
cos θ= 求值定角.
(2)a·b与|a||b|不好求,可采用寻求两者关系,再用
变形公式cos θ= 求值定角.2.两个向量的夹角与其数量积的关系
(1)向量a,b夹角为锐角的等价条件是a·b>0且a与b不同向共线.
(2)a,b夹角为钝角的等价条件是a·b<0且a与b不反向共线.
(3)a与b垂直的等价条件是a·b=0.【习练·破】
1.已知非零向量a,b,若a+3b与a-3b互相垂直,则 等
于 ( )
A. B.9 C. D.3【解析】选D.因为a+3b与a-3b互相垂直,
所以(a+3b)·(a-3b)=0,即|a|2-9|b|2=0.所以 =3.2.已知a,b满足|a|= ,|b|=2,|a+b|= ,求a+b与a-b的夹角的余弦值.【解析】由已知|a|= ,|b|=2,|a+b|= ,
所以(a+b)2=13.即a2+2a·b+b2=13,所以2a·b=6.
所以(a-b)2=a2-2a·b+b2=(a+b)2-4a·b=1.
即|a-b|=1,(a+b)·(a-b)=a2-b2=3-4=-1,
故cos= 【加练·固】
设向量a,b满足|a|=1,|b|=1,且a与b具有关系|ka+b|=
|a-kb|(k>0).
(1)a与b能垂直吗?
(2)若a与b夹角为60°,求k的值.【解析】(1)因为|ka+b|= |a-kb|,
所以(ka+b)2=3(a-kb)2,且|a|=|b|=1.
即k2+1+2ka·b=3(1+k2-2ka·b),
所以a·b= .
因为k2+1≠0,所以a·b≠0,即a与b不垂直.(2)因为a与b夹角为60°,且|a|=|b|=1,
所以a·b=|a||b|cos 60°= .
所以 = .所以k=1.类型三 平面向量在平面几何证明中的应用
【典例】1.(2019·潍坊高一检测)点O是△ABC所在平
面上的一点,且满足 ,则点O是
△ABC的 ( )
A.重心 B. 垂心
C. 内心 D. 外心2.如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE. 世纪金榜导学号【思维·引】1.恰当利用数量积的运算律,对已知等
式变形,证明有关直线垂直.
2.选择基底表示 和 ,转化为证明向量垂直.【解析】1.选B.因为 ,
所以 =0,即 =0,
所以 ,同理,
,所以O是△ABC的垂心.2.设 =a, =b,则|a|=|b|,a·b=0,
又 =-a+ ,
所以 =
故 ,即AF⊥DE.【类题·通】
利用向量的数量积解决几何问题
向量是数学中的一种常用工具,利用向量可以解决很多相关的几何问题,比如判断三角形的形状,四边形的形状等,在求解几何问题时如何把几何问题转化为向量问题,利用向量知识解答是解决问题的关键.【习练·破】
1.设平面上有四个互异的点A,B,C,D,已知
· =0,则△ABC是 ( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形【解析】选A.因为
即| |2-| |2=0,所以| |=| |.
所以△ABC为等腰三角形.2.已知:如图,AB是☉O的直径,点P是☉O上任一点(不与A,B重合),求证:∠APB=90°.(用向量方法证明)【证明】连接OP,设向量 =a, =b,
则|a|=|b|, =-a且 =a-b,
=-a-b,
所以 · =b2-a2=|b|2-|a|2=0,
所以 ⊥ ,
即∠APB=90°.【加练·固】
如图,点O是△ABC的外心,E为三角形内一点,
满足
求证: .【证明】因为O为外心,所以| |=| |.
因为
所以
=| |2-| |2=0,即 =0.
故 .类型四 利用向量的模长公式求力的大小
【物理情境】
一质点受到平面上的三个力F1,F2,F3(单位:N)的作用而处于平衡状态.已知F1,F2成60°角,且F1,F2的大小分别为2和3,求F3的大小.【转化模板】
1. —因为物理学中力是一个向量,所以求力的大小
可以转化为求向量的模的大小,力的平衡即向量的和
为零向量,可以建立向量模型解决.
2. —把三个力F1,F2,F3分别看作向量F1,F2,F3.3. —F1,F2,F3满足F1+F2+F3=0,|F1|=2,|F2|=3,
且F1,F2夹角为60°,求|F3|.
4. —由F1+F2+F3=0,得-F3=F1+F2,
所以|F3|2=(F1+F2)2=|F1|2+|F2|2+2|F1|·|F2|·
cos 60°=4+9+6=19,所以|F3|= .
5. —力F3的大小为 N.
(1)a·b=b·a(交换律).
(2)(λa)·b=λ(a·b)=a·(λb).
(3)(a+b)·c=a·c+b·c(分配律).【思考】
“若a·b=a·c,则b=c”成立吗?请说明原因.
提示:不成立.如a⊥b,a⊥c时,a·b=a·c,但b与c不一定相等.【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)(a·b)·c=a·(b·c). ( )
(2)(a·b)2=a2·b2. ( )
(3)a·[b(a·c)-c(a·b)]=0. ( )提示:(1)×.向量(a·b)·c与c共线,a·(b·c)与a共线,故不正确.
(2)×.(a·b)2=(|a||b|·cos θ)2=a2b2cos2θ.
(3)√.a·[b(a·c)-c(a·b)]=(a·b)(a·c)-(a·c)(a·b)=0.2.已知|a|=|b|=2,a·b=2,则|a-b|= ( )
A.1 B. C.2 D. 或2【解析】选C.|a-b|=
3.若向量a,b满足|a|=|b|=1,且a·(a-b)= ,则向量
a与b的夹角为 ( )
A. B. C. D. 【解析】选B.因为a·(a-b)=a2-a·b= ,
所以1-1×1×cos
所以cos
因为0≤
等于 ( )
A.- a2 B.- a2 C. a2 D. a2【解析】选D.如图所示,由题意,得BC=a, CD=a,∠BCD=120°.
所以
=a·a·cos 60°+a2= a2.类型一 向量数量积的运算律的应用
【典例】1.(2018·全国卷Ⅱ)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)= ( )
A.4 B.3 C.2 D.02.(2020·长春高二检测)已知向量|a+b|=|a-b|,且|a|=|b|=2,则|2a-b|= ( )
A.2 B.2 C.2 D. 3.(2020·马鞍山高一检测) 如图,四边形ABCD是边长
为2的菱形,∠BAD=60°,E,F分别为BC,CD的中点,
则 · = ( )
A. B.- C. D.- 【思维·引】
1.利用向量数量积的定义与运算律计算.
2.先利用|a+b|=|a-b|得出a·b=0,再利用a2=|a|2和
向量数量积运算律计算.
3.先分别用基向量 表示 ,再利用向量
数量积的定义与运算律计算.【解析】1.选B. a·(2a-b)=2a2-a·b=2-(-1)=3.
2.选C.因为向量|a+b|=|a-b|,
所以a·b=0,又|a|=|b|=2,
所以|2a-b|= =2 .3.选D. 因为菱形ABCD的边长为2,∠BAD=60°,
所以 =2×2×cos 60°=2,
又因为
所以 【内化·悟】
1.形如“a·(2a-b)”的计算将如何进行?
提示:类比单项式乘以多项式的计算方法进行.2.根据模长公式,求向量的模的问题应首先做怎样的转化?
提示:求模问题一般转化为求模的平方.3.如何解决几何图形中向量数量积的计算?
提示:一般选择已知长度与夹角的向量作基底,用基底表示要求数量积的向量,再计算.【类题·通】
向量数量积运算中的常用结论
(1)a2=|a|2.
(2)(xa+yb)·(mc+nd)=xma·c+xna·d+ymb·c+ynb·d,其中x,y,m,n∈R,类似于多项式的乘法法则.(3)(a+b)2=a2+2a·b+b2.
(4)(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c.【习练·破】
1.已知向量a与b的夹角为120°,且|a|=4,|b|=2,则(2a-b)·(a+3b)=________.?【解析】(2a-b)·(a+3b)=2a2+6a·b-a·b-3b2
=2|a|2+5a·b-3|b|2
=2×16+5×4×2×cos 120°-3×4=0.
答案:02.(2019·临沂高一检测)已知向量a,b满足|b|=5, |2a+b|=5 ,|a-b|=5 ,则|a|=________.?【解析】由已知有
将b2=|b|2=25代入方程组,解得|a|= .
答案: 【加练·固】
(2020·烟台高一检测)在△ABC中,已知| + |=
| - |,AB=1,AC=3,M,N分别为BC的三等分点(M靠
近B,N靠近C),则 · = ( )
A. B. C. D. 【解析】选B.因为| + |=| - |,
所以∠BAC=90°.又M,N分别为BC的三等分点, 类型二 向量的夹角和垂直问题
角度1 求向量的夹角
【典例】(2019·全国卷Ⅰ)已知非零向量a,b满足
|a|=2|b|,且(a-b)⊥b,则a与b的夹角为 ( )
A. B. C. D. 【思维·引】利用夹角公式计算.
【解析】选B.设夹角为θ,因为(a-b)⊥b,
所以(a-b)·b=a·b-b2=0,所以a·b=b2,
所以cos θ= ,又θ∈[0,π],
所以a与b的夹角为 ,故选B.【素养·探】
解决向量的夹角与垂直问题时,常常需要结合图形分析问题,突出体现了数学抽象和直观想象的核心素养.
若将本例条件改为“|a|=3|b|=|a+2b|”,试求a与b夹角的余弦值.【解析】设a与b夹角为θ,因为|a|=3|b|,
所以|a|2=9|b|2.
又|a|=|a+2b|,
所以|a|2=|a|2+4|b|2+4a·b
=|a|2+4|b|2+4|a|·|b|·cos θ=13|b|2+12|b|2cos θ,
即9|b|2=13|b|2+12|b|2cos θ,
故有cos θ=- .
角度2 向量垂直的应用
【典例】 (2019·枣庄高一检测)已知非零向量m,n的
夹角为θ,且满足4|m|=3|n|,cos θ= .
若n⊥(t m+n),则实数t的值为世纪金榜导学号( )
A.4 B.-4 C. D.- 【思维·引】利用向量垂直的充要条件求参数.
【解析】选B.由4|m|=3|n|,
可设|m|=3k,|n|=4k(k>0),
又n⊥(t m+n),所以n·(t m+n)=n·t m+n·n
=t|m|·|n|cos θ+|n|2
=t×3k×4k× +(4k)2
=4tk2+16k2=0.
所以t=-4.【类题·通】
1.求向量夹角问题一般有两种思路
(1)数量积a·b与模积|a||b|好求解,直接用变形公式
cos θ= 求值定角.
(2)a·b与|a||b|不好求,可采用寻求两者关系,再用
变形公式cos θ= 求值定角.2.两个向量的夹角与其数量积的关系
(1)向量a,b夹角为锐角的等价条件是a·b>0且a与b不同向共线.
(2)a,b夹角为钝角的等价条件是a·b<0且a与b不反向共线.
(3)a与b垂直的等价条件是a·b=0.【习练·破】
1.已知非零向量a,b,若a+3b与a-3b互相垂直,则 等
于 ( )
A. B.9 C. D.3【解析】选D.因为a+3b与a-3b互相垂直,
所以(a+3b)·(a-3b)=0,即|a|2-9|b|2=0.所以 =3.2.已知a,b满足|a|= ,|b|=2,|a+b|= ,求a+b与a-b的夹角的余弦值.【解析】由已知|a|= ,|b|=2,|a+b|= ,
所以(a+b)2=13.即a2+2a·b+b2=13,所以2a·b=6.
所以(a-b)2=a2-2a·b+b2=(a+b)2-4a·b=1.
即|a-b|=1,(a+b)·(a-b)=a2-b2=3-4=-1,
故cos
设向量a,b满足|a|=1,|b|=1,且a与b具有关系|ka+b|=
|a-kb|(k>0).
(1)a与b能垂直吗?
(2)若a与b夹角为60°,求k的值.【解析】(1)因为|ka+b|= |a-kb|,
所以(ka+b)2=3(a-kb)2,且|a|=|b|=1.
即k2+1+2ka·b=3(1+k2-2ka·b),
所以a·b= .
因为k2+1≠0,所以a·b≠0,即a与b不垂直.(2)因为a与b夹角为60°,且|a|=|b|=1,
所以a·b=|a||b|cos 60°= .
所以 = .所以k=1.类型三 平面向量在平面几何证明中的应用
【典例】1.(2019·潍坊高一检测)点O是△ABC所在平
面上的一点,且满足 ,则点O是
△ABC的 ( )
A.重心 B. 垂心
C. 内心 D. 外心2.如图所示,在正方形ABCD中,E,F分别是AB,BC的中点,求证:AF⊥DE. 世纪金榜导学号【思维·引】1.恰当利用数量积的运算律,对已知等
式变形,证明有关直线垂直.
2.选择基底表示 和 ,转化为证明向量垂直.【解析】1.选B.因为 ,
所以 =0,即 =0,
所以 ,同理,
,所以O是△ABC的垂心.2.设 =a, =b,则|a|=|b|,a·b=0,
又 =-a+ ,
所以 =
故 ,即AF⊥DE.【类题·通】
利用向量的数量积解决几何问题
向量是数学中的一种常用工具,利用向量可以解决很多相关的几何问题,比如判断三角形的形状,四边形的形状等,在求解几何问题时如何把几何问题转化为向量问题,利用向量知识解答是解决问题的关键.【习练·破】
1.设平面上有四个互异的点A,B,C,D,已知
· =0,则△ABC是 ( )
A.等腰三角形 B.直角三角形
C.等腰直角三角形 D.等边三角形【解析】选A.因为
即| |2-| |2=0,所以| |=| |.
所以△ABC为等腰三角形.2.已知:如图,AB是☉O的直径,点P是☉O上任一点(不与A,B重合),求证:∠APB=90°.(用向量方法证明)【证明】连接OP,设向量 =a, =b,
则|a|=|b|, =-a且 =a-b,
=-a-b,
所以 · =b2-a2=|b|2-|a|2=0,
所以 ⊥ ,
即∠APB=90°.【加练·固】
如图,点O是△ABC的外心,E为三角形内一点,
满足
求证: .【证明】因为O为外心,所以| |=| |.
因为
所以
=| |2-| |2=0,即 =0.
故 .类型四 利用向量的模长公式求力的大小
【物理情境】
一质点受到平面上的三个力F1,F2,F3(单位:N)的作用而处于平衡状态.已知F1,F2成60°角,且F1,F2的大小分别为2和3,求F3的大小.【转化模板】
1. —因为物理学中力是一个向量,所以求力的大小
可以转化为求向量的模的大小,力的平衡即向量的和
为零向量,可以建立向量模型解决.
2. —把三个力F1,F2,F3分别看作向量F1,F2,F3.3. —F1,F2,F3满足F1+F2+F3=0,|F1|=2,|F2|=3,
且F1,F2夹角为60°,求|F3|.
4. —由F1+F2+F3=0,得-F3=F1+F2,
所以|F3|2=(F1+F2)2=|F1|2+|F2|2+2|F1|·|F2|·
cos 60°=4+9+6=19,所以|F3|= .
5. —力F3的大小为 N.
