新教材人教B版数学必修第三册课件:8.2.1 两角和与差的余弦(57张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:8.2.1 两角和与差的余弦(57张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览











文档简介
课件57张PPT。8.2 三角恒等变换
8.2.1 两角和与差的余弦两角和与差的余弦公式【思考】
(1)两角和的余弦公式是怎样由两角差的余弦公式推导而来的?
提示:在两角差的余弦公式cos(α-β)=cos αcos β
+sin αsin β中,只要用-β替换β,便可以得到两角和的余弦公式. (2)两角和与差的余弦公式的结构特征是什么?可用什么口诀记忆?
提示:可简单记为“余余正正,符号反”,即展开后的两项分别为两角的余弦乘余弦、正弦乘正弦;展开前两角间的符号与展开后两项间的符号相反. 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)cos(70°+40°)=cos 70°-cos 40°. ( )
(2)对于任意实数α,β,cos(α-β)=cos α-cos β都不成立. ( )(3)对任意α,β∈R,cos(α+β)=cos αcos β-
sin αsin β都成立. ( )
(4)cos 30°cos60°+sin 30°sin 60°=1. ( )提示:(1)×.cos(70°+40°)=cos 110°≠cos 70°
-cos 40°.
(2)×.当α=-45°,β=45°时,cos(α-β)=
cos(-45°-45°)=cos(-90°)=0,cos α-cos β
=cos(-45°)-cos 45°=0,此时cos(α-β)=cos α-cos β.(3)√.结论为两角和的余弦公式.
(4) ×.cos 30°cos 60°+sin 30°sin 60°
=cos(60°-30°)=cos 30°= .2.cos 75°cos 15°-sin 75°sin 15°的值等于
________.?
【解析】逆用两角和的余弦公式可得:
cos 75°cos 15°-sin 75°sin 15°
=cos(75°+15°)=cos 90°=0.
答案:03.cos 15°=________.?
【解析】cos 15°=cos(45°-30°)
=cos 45°·cos 30°+sin 45°·sin 30°
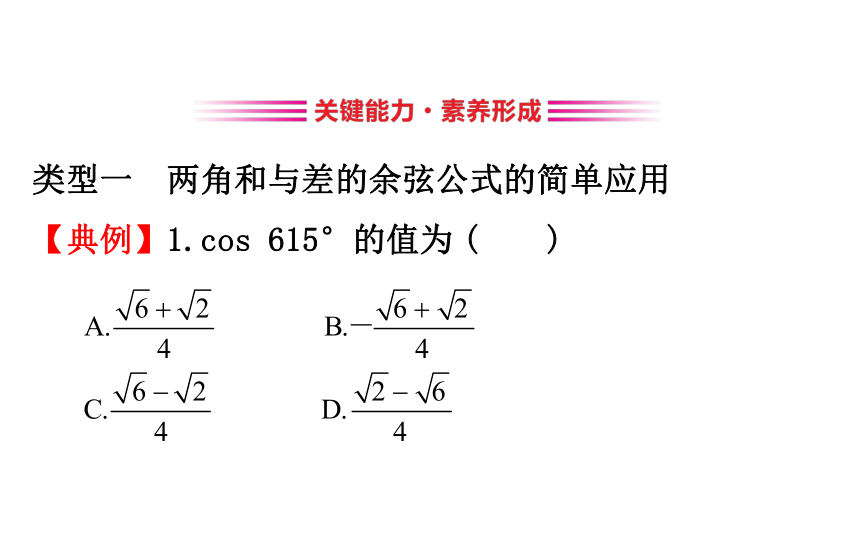
答案: 类型一 两角和与差的余弦公式的简单应用
【典例】1.cos 615°的值为 ( )2.计算sin 7°cos 23°+sin 83°cos 67°的值为
( )【思维·引】1.把615°转化为两个特殊角的差,进一步转化利用两角和的余弦公式求解.
2.先利用诱导公式对角进行转化,再逆用两角差的余弦公式求解.【解析】1.选D.cos 615°=cos(720°-105°)=
cos 105°=cos(45°+60°)= .
2.选B.sin 7°cos 23°+sin 83°cos 67°=
cos 83°cos 23°+sin 83°sin 23°=cos(83°-
23°)=cos 60°= .【内化·悟】
一般地,利用两角和与差的余弦公式可以解决什么类型的题目?
提示:(1)求非特殊角的余弦值;(2)求两角的同名三角函数积的和或差.【类题·通】
利用两角和与差的余弦公式解含非特殊角的三角函数式的求值问题的一般思路
(1)把非特殊角转化为特殊角的和或差,后用公式直接求值;
(2)充分利用诱导公式,构造两角和与差的余弦公式的结构形式,然后逆用公式求值.【习练·破】
求下列各式的值:(1)cos .
(2)sin 400°sin(-160°)+cos 560°cos(-220°).【解析】(1)cos =cos =-cos
=-cos =-cos (2)原式=-sin 40°sin 160°+cos 200°cos 220°
=-sin 40°sin 20°+cos 20°cos 40°
=cos 40°cos 20°-sin 40°sin 20°
=cos 60°= .【加练·固】
1. sin +cos 的值为 ( )
A. B.1 C. D. 【解析】选C.原式=2
2cos =2cos =2× .2.cos(α-20°)cos(40°+α)+sin(α-20°)sin(40°+α)=__________.?【解析】cos(α-20°)cos(40°+α)+sin(α-20°)
·sin(40°+α)
=cos[(α-20°)-(α+40°)]
=cos(-60°)= .
答案: 类型二 给值求值问题
角度1 代入求值问题
【典例】已知sin ,则cos α+ sin α的
值为 ( )
A. B. C.2 D.-1【思维·引】对所求式逐步变形,直至可代入已知条
件即可.
【解析】选B.cos α+ sin α=
2 =2cos
=2sin =2sin =2× .【发散·拓】
常值代换
用某些三角函数值代替某些常数,使之代换后能运用相关的公式,我们把这种代换称为常值代换,其中特别要注意的是“1”的代换.如1=sin2α+cos2α,1=tan 45°,1=sin 90°等.再如
等均可视为某个特殊的三角函数值,从
而将常数代换为三角函数使用.【延伸·练】 cos 15°+ sin 15°=________.?
【解析】因为 =cos 60°, =sin 60°,
所以 cos 15°+ sin 15°=cos 60°cos 15°
+sin 60°sin 15°=cos(60°-15°)=cos 45°= .
答案: 角度2 角的“拼凑”问题
【典例】设α,β都是锐角,且cos α= ,sin(α+
β)= ,则cos β等于 世纪金榜导学号( )
A. B.
C. D. 【思维·引】考虑如何用已知角α,α+β的差来表示所求角β,进而利用两角差的余弦公式解决.【解析】选A.依题意得sin α= ,
cos(α+β)=± .
又α,β均为锐角,
所以0<α<α+β<π,cos α>cos(α+β).因为 ,所以cos(α+β)= .
于是cos β=cos[(α+β)-α]=cos(α+β)cos α
+sin(α+β)sin α= 【素养·探】
本例主要考查三角函数求值问题,突出考查了数学运
算的核心素养.
本例若改为:已知α,β为锐角,且cos α= ,
cos(α+β)= ,求cos β的值.【解析】因为0<α< ,0<β< ,所以0<α+β<π.
由cos(α+β)= ,得sin(α+β)= .
又因为cos α= ,所以sin α= .
所以cos β=cos[(α+β)-α]
=cos(α+β)cos α+sin(α+β)sin α【类题·通】
1.解决三角函数求值问题的关键是把“所求角”用“已知角”表示.
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.2.常见的配角技巧:2α=(α+β)+(α-β),
α=(α+β)-β,β=
等.【习练·破】
1.已知α为锐角,β为第三象限角,且cos α= ,
sin β= ,则cos(α+β)的值为 ( )【解析】选B.因为α为锐角,且cos α= ,所以
sin α= .因为β为第三象限角,且
sin β= ,所以cos β= ,所以cos(α+β)=cos αcos β-sin αsin β
= 2.已知cos ,则cos α+ sin α的值为
________.?
【解析】因为cos =cos cos α+sin sinα
= cos α+ sin α= ,所以cos α+ sin α
= .
答案: 【加练·固】
若0<α< ,- <β<0,cos ,cos ,
则cos = ( )【解析】选C.cos =cos =
cos cos +sin sin ,而
+α∈
因此sin ,sin
则cos 类型三 给值求角问题
【典例】已知cos(α-β)= ,sin(α+β)= ,
<α-β<π, <α+β<2π,求β的值. 世纪金榜导
学号【思维·引】先求2β的余弦值,再由角的范围确定2β及β的大小.【解析】因为 <α-β<π,cos(α-β)= ,
所以sin(α-β)= .因为 π<α+β<2π,sin(α+
β)= ,所以cos(α+β)= ,
所以cos 2β=cos[(α+β)-(α-β)]
=cos(α+β)cos(α-β)+sin(α+β)sin(α-β) =-1.因为 <α-β<π,
π<α+β<2π,所以 <2β< ,所以2β=π,所
以β= .【内化·悟】
解决给值求角问题的关键环节是什么?
提示:关键环节有两点:
(1)求出所求角的某种三角函数值;(2)确定角的范围.做好这两个环节,结合三角函数的性质与图像,角可求解.【类题·通】
解决给值求角问题的一般步骤
(1)求角的某一个三角函数值;
(2)确定角的范围;
(3)根据角的范围写出要求的角.【习练·破】
1.已知sin α= ,sin β= ,且α和β均为钝角,
则α+β=________.?【解析】因为α,β均为钝角,
所以cos α=
cos β=
所以cos (α+β)=cos αcos β-sin αsin β= 由α和β均为钝角,得π<α+β<2π,所以α+β= .
答案: 2.已知sin ,sin ,且α- ∈
,β- ∈ ,则 的值为________.?【解析】因为α- ,所以
0< <π,
因为sin ,所以cos ,
因为sin ,所以cos .
再由cos =cos =cos cos -sin sin
所以
答案: 【加练·固】
已知向量a=(cos α,sin α),b=(cos β,sin β),
α,β∈(0,π)且a⊥b,求α-β的值.【解析】因为a⊥b,所以a·b=0,
即cos α cos β+sin α sin β=0.
从而cos(α-β)=0.因为α,β∈(0,π),
所以-π<α-β<π,
所以α-β= 或- .
8.2.1 两角和与差的余弦两角和与差的余弦公式【思考】
(1)两角和的余弦公式是怎样由两角差的余弦公式推导而来的?
提示:在两角差的余弦公式cos(α-β)=cos αcos β
+sin αsin β中,只要用-β替换β,便可以得到两角和的余弦公式. (2)两角和与差的余弦公式的结构特征是什么?可用什么口诀记忆?
提示:可简单记为“余余正正,符号反”,即展开后的两项分别为两角的余弦乘余弦、正弦乘正弦;展开前两角间的符号与展开后两项间的符号相反. 【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)cos(70°+40°)=cos 70°-cos 40°. ( )
(2)对于任意实数α,β,cos(α-β)=cos α-cos β都不成立. ( )(3)对任意α,β∈R,cos(α+β)=cos αcos β-
sin αsin β都成立. ( )
(4)cos 30°cos60°+sin 30°sin 60°=1. ( )提示:(1)×.cos(70°+40°)=cos 110°≠cos 70°
-cos 40°.
(2)×.当α=-45°,β=45°时,cos(α-β)=
cos(-45°-45°)=cos(-90°)=0,cos α-cos β
=cos(-45°)-cos 45°=0,此时cos(α-β)=cos α-cos β.(3)√.结论为两角和的余弦公式.
(4) ×.cos 30°cos 60°+sin 30°sin 60°
=cos(60°-30°)=cos 30°= .2.cos 75°cos 15°-sin 75°sin 15°的值等于
________.?
【解析】逆用两角和的余弦公式可得:
cos 75°cos 15°-sin 75°sin 15°
=cos(75°+15°)=cos 90°=0.
答案:03.cos 15°=________.?
【解析】cos 15°=cos(45°-30°)
=cos 45°·cos 30°+sin 45°·sin 30°
答案: 类型一 两角和与差的余弦公式的简单应用
【典例】1.cos 615°的值为 ( )2.计算sin 7°cos 23°+sin 83°cos 67°的值为
( )【思维·引】1.把615°转化为两个特殊角的差,进一步转化利用两角和的余弦公式求解.
2.先利用诱导公式对角进行转化,再逆用两角差的余弦公式求解.【解析】1.选D.cos 615°=cos(720°-105°)=
cos 105°=cos(45°+60°)= .
2.选B.sin 7°cos 23°+sin 83°cos 67°=
cos 83°cos 23°+sin 83°sin 23°=cos(83°-
23°)=cos 60°= .【内化·悟】
一般地,利用两角和与差的余弦公式可以解决什么类型的题目?
提示:(1)求非特殊角的余弦值;(2)求两角的同名三角函数积的和或差.【类题·通】
利用两角和与差的余弦公式解含非特殊角的三角函数式的求值问题的一般思路
(1)把非特殊角转化为特殊角的和或差,后用公式直接求值;
(2)充分利用诱导公式,构造两角和与差的余弦公式的结构形式,然后逆用公式求值.【习练·破】
求下列各式的值:(1)cos .
(2)sin 400°sin(-160°)+cos 560°cos(-220°).【解析】(1)cos =cos =-cos
=-cos =-cos (2)原式=-sin 40°sin 160°+cos 200°cos 220°
=-sin 40°sin 20°+cos 20°cos 40°
=cos 40°cos 20°-sin 40°sin 20°
=cos 60°= .【加练·固】
1. sin +cos 的值为 ( )
A. B.1 C. D. 【解析】选C.原式=2
2cos =2cos =2× .2.cos(α-20°)cos(40°+α)+sin(α-20°)sin(40°+α)=__________.?【解析】cos(α-20°)cos(40°+α)+sin(α-20°)
·sin(40°+α)
=cos[(α-20°)-(α+40°)]
=cos(-60°)= .
答案: 类型二 给值求值问题
角度1 代入求值问题
【典例】已知sin ,则cos α+ sin α的
值为 ( )
A. B. C.2 D.-1【思维·引】对所求式逐步变形,直至可代入已知条
件即可.
【解析】选B.cos α+ sin α=
2 =2cos
=2sin =2sin =2× .【发散·拓】
常值代换
用某些三角函数值代替某些常数,使之代换后能运用相关的公式,我们把这种代换称为常值代换,其中特别要注意的是“1”的代换.如1=sin2α+cos2α,1=tan 45°,1=sin 90°等.再如
等均可视为某个特殊的三角函数值,从
而将常数代换为三角函数使用.【延伸·练】 cos 15°+ sin 15°=________.?
【解析】因为 =cos 60°, =sin 60°,
所以 cos 15°+ sin 15°=cos 60°cos 15°
+sin 60°sin 15°=cos(60°-15°)=cos 45°= .
答案: 角度2 角的“拼凑”问题
【典例】设α,β都是锐角,且cos α= ,sin(α+
β)= ,则cos β等于 世纪金榜导学号( )
A. B.
C. D. 【思维·引】考虑如何用已知角α,α+β的差来表示所求角β,进而利用两角差的余弦公式解决.【解析】选A.依题意得sin α= ,
cos(α+β)=± .
又α,β均为锐角,
所以0<α<α+β<π,cos α>cos(α+β).因为 ,所以cos(α+β)= .
于是cos β=cos[(α+β)-α]=cos(α+β)cos α
+sin(α+β)sin α= 【素养·探】
本例主要考查三角函数求值问题,突出考查了数学运
算的核心素养.
本例若改为:已知α,β为锐角,且cos α= ,
cos(α+β)= ,求cos β的值.【解析】因为0<α< ,0<β< ,所以0<α+β<π.
由cos(α+β)= ,得sin(α+β)= .
又因为cos α= ,所以sin α= .
所以cos β=cos[(α+β)-α]
=cos(α+β)cos α+sin(α+β)sin α【类题·通】
1.解决三角函数求值问题的关键是把“所求角”用“已知角”表示.
(1)当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;(2)当“已知角”有一个时,此时应着眼于“所求角”与“已知角”的和或差的关系,然后应用诱导公式把“所求角”变成“已知角”.2.常见的配角技巧:2α=(α+β)+(α-β),
α=(α+β)-β,β=
等.【习练·破】
1.已知α为锐角,β为第三象限角,且cos α= ,
sin β= ,则cos(α+β)的值为 ( )【解析】选B.因为α为锐角,且cos α= ,所以
sin α= .因为β为第三象限角,且
sin β= ,所以cos β= ,所以cos(α+β)=cos αcos β-sin αsin β
= 2.已知cos ,则cos α+ sin α的值为
________.?
【解析】因为cos =cos cos α+sin sinα
= cos α+ sin α= ,所以cos α+ sin α
= .
答案: 【加练·固】
若0<α< ,- <β<0,cos ,cos ,
则cos = ( )【解析】选C.cos =cos =
cos cos +sin sin ,而
+α∈
因此sin ,sin
则cos 类型三 给值求角问题
【典例】已知cos(α-β)= ,sin(α+β)= ,
<α-β<π, <α+β<2π,求β的值. 世纪金榜导
学号【思维·引】先求2β的余弦值,再由角的范围确定2β及β的大小.【解析】因为 <α-β<π,cos(α-β)= ,
所以sin(α-β)= .因为 π<α+β<2π,sin(α+
β)= ,所以cos(α+β)= ,
所以cos 2β=cos[(α+β)-(α-β)]
=cos(α+β)cos(α-β)+sin(α+β)sin(α-β) =-1.因为 <α-β<π,
π<α+β<2π,所以 <2β< ,所以2β=π,所
以β= .【内化·悟】
解决给值求角问题的关键环节是什么?
提示:关键环节有两点:
(1)求出所求角的某种三角函数值;(2)确定角的范围.做好这两个环节,结合三角函数的性质与图像,角可求解.【类题·通】
解决给值求角问题的一般步骤
(1)求角的某一个三角函数值;
(2)确定角的范围;
(3)根据角的范围写出要求的角.【习练·破】
1.已知sin α= ,sin β= ,且α和β均为钝角,
则α+β=________.?【解析】因为α,β均为钝角,
所以cos α=
cos β=
所以cos (α+β)=cos αcos β-sin αsin β= 由α和β均为钝角,得π<α+β<2π,所以α+β= .
答案: 2.已知sin ,sin ,且α- ∈
,β- ∈ ,则 的值为________.?【解析】因为α- ,所以
0< <π,
因为sin ,所以cos ,
因为sin ,所以cos .
再由cos =cos =cos cos -sin sin
所以
答案: 【加练·固】
已知向量a=(cos α,sin α),b=(cos β,sin β),
α,β∈(0,π)且a⊥b,求α-β的值.【解析】因为a⊥b,所以a·b=0,
即cos α cos β+sin α sin β=0.
从而cos(α-β)=0.因为α,β∈(0,π),
所以-π<α-β<π,
所以α-β= 或- .
