新教材人教B版数学必修第三册课件:8.2.2 两角和与差的正弦、正切(92张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:8.2.2 两角和与差的正弦、正切(92张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览







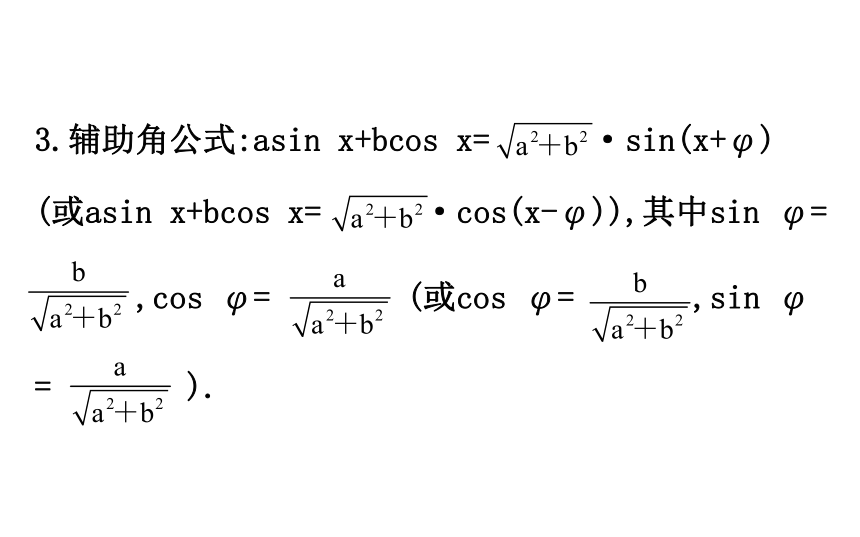

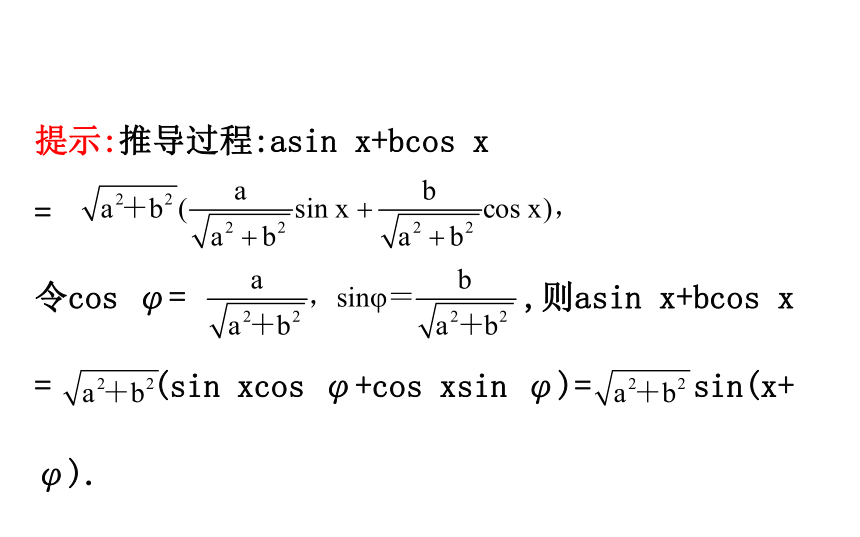
文档简介
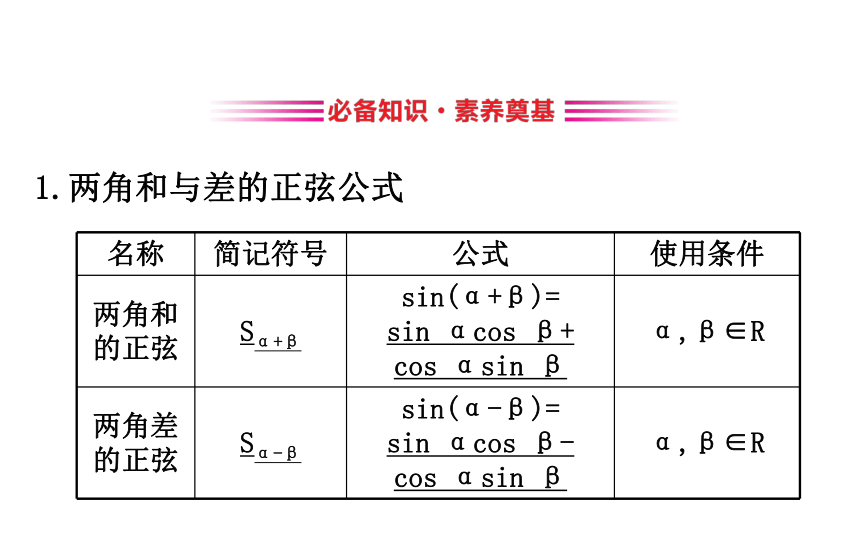
课件92张PPT。8.2.2 两角和与差的正弦、正切1.两角和与差的正弦公式【思考】
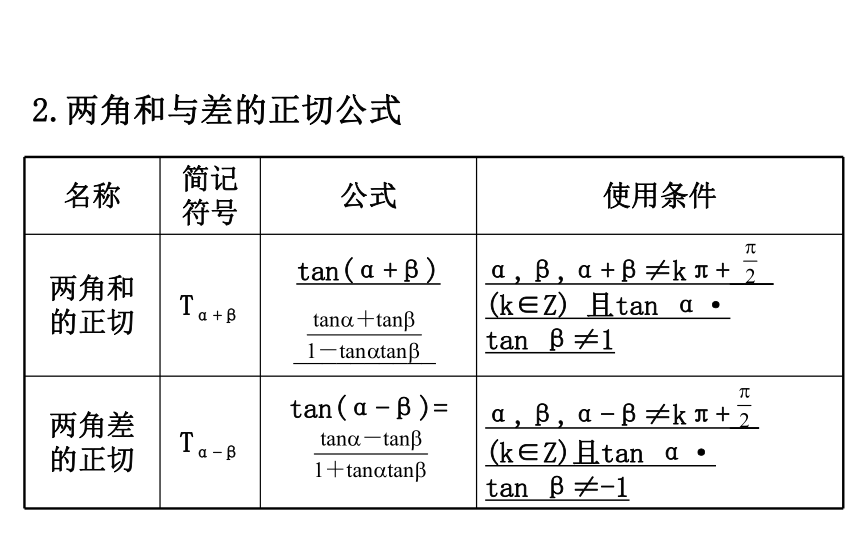
对照识记两角和与差的余弦公式的方法,你能总结一下识记两角和与差的正弦公式的方法吗?提示:可简单记为“正余余正,符号同”,即展开后的两项分别为两角的正弦乘余弦、余弦乘正弦;展开前两角间的符号与展开后两项间的符号相同.2.两角和与差的正切公式【思考】
(1)由同角三角函数的商数关系知tan(α+β)=
由此能否推导出两角和的正切公式?提示:能.
tan(α+β)= ,分子分母同除
以cos αcos β可得tan(α+β)= (2)两角和与差的正切公式中为什么限制α,β,α+β,
α-β都不等于kπ+ (k∈Z)?
提示:这是由正切函数的定义域决定的.3.辅助角公式:asin x+bcos x= ·sin(x+φ)
(或asin x+bcos x= ·cos(x-φ)),其中sin φ=
,cos φ= (或cos φ= ,sin φ
= ).【思考】
辅助角公式是如何推导出来的?提示:推导过程:asin x+bcos x
=
令cos φ= ,则asin x+bcos x
= (sin xcos φ+cos xsin φ)= sin(x+
φ).【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)两角和与差的正弦、余弦公式中的角α,β是任意的. ( )
(2)存在α,β∈R,使得sin(α+β)=sin α+sin β成立. ( )(3)对任意α,β∈R,tan(α+β)= 都成
立. ( )
(4)sin 56°cos 26°-cos56°sin 26°=
sin 30°. ( )提示:(1)√.根据公式的推导过程可得.
(2)√.当α=30°,β=0°时,sin(α+β)=sin α
+sin β.
(3)×.两角和的正切公式的适用范围是α,β,α+β
≠kπ+ (k∈Z)且tan α·tan β≠1.(4)√.因为sin 56°cos 26°-cos 56°sin 26°
=sin(56°-26°)=sin 30°,故原式正确. ( ) 【解析】选C. 3.计算sin =________.?【解析】
答案: 类型一 两角和与差的正弦公式的应用
角度1 化简、求值问题
【典例】1.(2019·河东高一检测) 的值
是 ( )2.(2018·全国卷Ⅱ)已知sin α+cos β=1,cos α+
sin β=0,则sin(α+β)=________.?
3.若 ,则
cos(α+β)的值为________.?【思维·引】1.由sin 40°=sin 套用两角差
的正弦公式化简可求值.
2.把两个已知条件分别平方,求和,利用两角和的正弦
公式可得答案.
3.考虑如何利用已知条件中的角拼凑成所求问题中的
角,可使用诱导公式.【解析】1.选A.原式= 2.由sin α+cos β=1与cos α+sin β=0分别平方相
加得sin2α+2sin αcos β+cos2β+cos2α+
2cos αsin β+sin2 β=1,即2+2sin αcos β+2cos αsin β=1,所以sin(α
+β)=- .
答案:- 3.因为0<α< +α<π,- -β
<0,
又已知sin
所以cos 所以cos(α+β)=
答案:- 【素养·探】
本例1考查利用两角和与差的正弦公式解决给角求值问
题,突出考查了数学抽象与数学运算的核心素养.若本
例1变形为下式,试求值.
的值是 ( )【解析】选A.原式= 角度2 求角与求点的坐标问题
【典例】1.已知α,β均为锐角,且sin α= ,cos β
= ,则α-β=________.?
2.已知向量 , 将向量 绕原点O顺时针旋转
60°到 的位置,则点A′的坐标为________.?【思维·引】
1.先由已知的三角函数值,选择适当的三角函数名求出所求角的三角函数值,再由已知角的范围,确定所求角的值.
2.利用向量的几何意义、三角函数的定义、两角差的正余弦公式解答.【解析】1.因为α,β均为锐角,且sin α= ,cos β
= ,
所以cos α= ,sin β=
所以sin (α-β)=sin αcos β-cos αsin β=又因为α,β均为锐角,所以- <α-β< ,故α-
β=- .
答案:- 2.如图,设A′ , ∠xOA=α, 所以∠xOA′=α-60°,则 =13,所以cos α= ,sin α= ,
因此x=13cos
同理y= ,所以A′
答案: 【类题·通】
1.解决给角求值问题的策略
(1)对于非特殊角的三角函数式求值问题,一定要本着先整体后局部的基本原则,如果整体符合三角公式的形式,则整体变形,否则进行各局部的变形.(2)解决三角函数的给值求值问题的关键是寻求“已知角”与“所求角”之间的关系,用“已知角”表示“所求角”.2.解决给值求角问题的一般思路
(1)确定角的范围;
(2)求角的正弦或余弦值;
(3)根据角的范围写出要求的角. 【习练·破】
1.已知cos (α为锐角),则sin α= ( )【解析】选D.因为α∈
所以α+
2.已知α,β为锐角,cos α= ,sin(α+β)= ,
则β=________.?【解析】因为α为锐角,且cos α= ,
所以sin α=
又α,β为锐角,所以α+β∈(0,π).
又sin(α+β)=所以cos(α+β)=- 所以cos β=cos[(α+β)-α]=cos(α+β)cos α
+sin(α+β)sin α
=
又β为锐角,所以β=
答案: 【加练·固】
1.化简下列各式:【解析】2.在△ABC中,3sin A+4cos B=6,3cos A+4sin B=1,则C的大小为 ( )【解析】选A.由已知可得(3sin A+4cos B)2+(3cos A+
4sin B)2=62+12,即9+16+24sin(A+B)=37.所以sin(A+B)
= .所以在△ABC中,sin C= ,所以C= 或C= .
又1-3cos A=4sin B>0,所以cos A< .
又 ,所以A> ,所以C< ,
所以C= 不符合题意,所以C= .类型二 两角和与差的正切公式的应用
【典例】1.计算 =________.?
2.tan 72°-tan 42°- tan 72°tan 42°=
________.?3.如图,在平面直角坐标系xOy中,以
Ox轴为始边作两个锐角α,β,它们的
终边分别与单位圆交于A,B两点.已知
A,B的横坐标分别为 .求:
(1)tan(α+β)的值;(2)α+2β的值. 世纪金榜导学号【思维·引】1.先用“tan45°=1”替换,再利用两角和的正切公式求值.
2.利用两角差的正切公式的变形公式解决.
3.(1)由三角函数的定义得出角α,β的正弦、余弦值,求出它们的正切值,利用两角和的正切公式解决.
(2)由α+2β=(α+β)+β,利用两角和的正切公式解决.【解析】1.原式= tan(45°
+15°)= tan 60°=1.
答案:12.原式=tan(72°-42°)(1+tan 72°·tan 42°)-
tan 72°tan 42°=tan 30°(1+tan 72°tan 42°)
-tan 30°tan 72°tan 42°=tan 30°= .
答案: 3.(1)由已知条件及三角函数的定义可知,
cos α= .因为α为锐角,故sin α>0,
从而sin α=
同理可得sin β= .因此tan α=7,tan β= .即tan(α+β)= =-3.(2)tan(α+2β)=tan[(α+β)+β]= =-1.
又0<α< ,0<β< ,故0<α+2β<
从而由tan(α+2β)=-1得α+2β= π.【内化·悟】
若已知条件中有角的正切值,一般的解决思路是什么?
提示:(1)切化弦,利用和差的正弦、余弦公式;(2)直接利用和差的正切公式.【类题·通】
1.公式Tα+β,Tα-β 应用的解题策略
(1)公式Tα+β,Tα-β有tan α·tan β,tan α+tan β(或tan α
-tan β),tan(α+β)(或tan(α-β)).三者知二可求出第三个;
(2)化简过程中注意“1”与“tan ”,“ ”与“tan ”
等特殊数与特殊角的函数值之间的转化.2.解决给值求角问题的选择原则
(1)已知正切函数值,选正切函数;
(2)已知正余弦函数值,选正弦或余弦函数,若角的范围是 ,
选正弦或余弦函数均可;若角的范围是(0,π),选余弦较好;若角
的范围是 ,选正弦较好.【习练·破】
1.求值:(1) 【解析】
(1)
(2)原式= =tan(45°+75°)=tan 120°
=- .2.已知tan(α-β)= ,tan β=- ,且α,β∈(-π,
0),求2α-β的值.【解析】因为α=(α-β)+β,tan(α-β)= ,tan β
=- ,α,β∈(-π,0),所以tan α=tan[(α-β)+β]
.又2α-β=α+(α-β),所以tan(2α-β)=tan[α+(α-β)]
=
而tan α= >0,tan β=- <0,α,β∈(-π,0),
则α∈ ,所以α-β∈(-π,0),而tan(α-β)= >0,则α-β∈
结合α∈ ,则有2α-β∈(-2π,-π),
所以2α-β=- .【加练·固】
1.tan 10°tan 20°+ (tan 10°+tan 20°)= ( ) 【解析】选B.原式=tan 10°tan 20°+ (1-
tan 10°tan 20°)·tan(10°+20°)=
tan 10°tan 20°+1-tan 10°tan 20°=1.2.在△ABC中,C=120°,tan A+tan B= ,则
tan Atan B的值为 ( )【解析】选B.因为C=120°,所以A+B=60°,
所以tan (A+B)=
因为tan A+tan B= ,
所以tan A+tan B= (1-tan A·tan B)= ,
解得tan A·tan B= .3.已知α,β,γ都是锐角,且tan α= ,tan β= ,
tan γ= ,则α+β+γ=________.?【解析】因为tan(α+β)=
tan(α+β+γ)= =1,因为tan α= ,且α为锐角,
所以0<α< ,同理0<β< ,0<γ< ,
所以0<α+β+γ< ,所以α+β+γ= .
答案: 类型三 辅助角公式的应用
【典例】1.cos α- sin α化简的结果可以是 ( ) 2.若函数f(x)=5cos x+12sin x在x=θ时取得最小值,
则cos θ等于 世纪金榜导学号( )【思维·引】利用辅助角公式进行变形.【解析】1.选B.cos α- sin α=
2.选B.f(x)=5cos x+12sin x
=
其中sin α= ,cos α= ,
由题意知θ+α=2kπ- (k∈Z)得θ=2kπ- -
α(k∈Z),所以 【内化·悟】
形如 sin α±cos α的式子通常如何变形?
提示: sin α±cos α=2 【类题·通】
把形如y=asin x+bcos x的式子化为y= sin(x+
φ),可进一步研究函数的周期性、单调性、最值与对
称性.【习练·破】
1.函数f(x)=sin x-cos x,x∈ 的最小值为( )
A.-2 B.- C.- D.-1【解析】选D.f(x)= ,因为0≤x≤ ,
所以- ,-
所以f(x)的最小值为-1.2.已知 的值为 ( ) 【解析】选B. 【加练·固】
1.(2018·全国卷Ⅱ)若f(x)=cos x-sin x在[-a,a]上
是减函数,则a的最大值是 ( )【解析】选A.f(x)=cos x-sin x=
上单调递减,所以[-a,a]?
故-a≥- 且a≤ ,解得0a的取值范围可以是 ( )【解析】选D.因为f(x)=3sin x-4cos x=5sin(x-
φ)
则sin(a-φ)=±1,
所以a-φ=kπ+ ,k∈Z,
即a=kπ+ +φ,k∈Z,而tan φ= 且0<φ< ,
所以 <φ< ,
所以kπ+
对照识记两角和与差的余弦公式的方法,你能总结一下识记两角和与差的正弦公式的方法吗?提示:可简单记为“正余余正,符号同”,即展开后的两项分别为两角的正弦乘余弦、余弦乘正弦;展开前两角间的符号与展开后两项间的符号相同.2.两角和与差的正切公式【思考】
(1)由同角三角函数的商数关系知tan(α+β)=
由此能否推导出两角和的正切公式?提示:能.
tan(α+β)= ,分子分母同除
以cos αcos β可得tan(α+β)= (2)两角和与差的正切公式中为什么限制α,β,α+β,
α-β都不等于kπ+ (k∈Z)?
提示:这是由正切函数的定义域决定的.3.辅助角公式:asin x+bcos x= ·sin(x+φ)
(或asin x+bcos x= ·cos(x-φ)),其中sin φ=
,cos φ= (或cos φ= ,sin φ
= ).【思考】
辅助角公式是如何推导出来的?提示:推导过程:asin x+bcos x
=
令cos φ= ,则asin x+bcos x
= (sin xcos φ+cos xsin φ)= sin(x+
φ).【素养小测】
1.思维辨析(对的打“√”,错的打“×”)
(1)两角和与差的正弦、余弦公式中的角α,β是任意的. ( )
(2)存在α,β∈R,使得sin(α+β)=sin α+sin β成立. ( )(3)对任意α,β∈R,tan(α+β)= 都成
立. ( )
(4)sin 56°cos 26°-cos56°sin 26°=
sin 30°. ( )提示:(1)√.根据公式的推导过程可得.
(2)√.当α=30°,β=0°时,sin(α+β)=sin α
+sin β.
(3)×.两角和的正切公式的适用范围是α,β,α+β
≠kπ+ (k∈Z)且tan α·tan β≠1.(4)√.因为sin 56°cos 26°-cos 56°sin 26°
=sin(56°-26°)=sin 30°,故原式正确. ( ) 【解析】选C. 3.计算sin =________.?【解析】
答案: 类型一 两角和与差的正弦公式的应用
角度1 化简、求值问题
【典例】1.(2019·河东高一检测) 的值
是 ( )2.(2018·全国卷Ⅱ)已知sin α+cos β=1,cos α+
sin β=0,则sin(α+β)=________.?
3.若 ,则
cos(α+β)的值为________.?【思维·引】1.由sin 40°=sin 套用两角差
的正弦公式化简可求值.
2.把两个已知条件分别平方,求和,利用两角和的正弦
公式可得答案.
3.考虑如何利用已知条件中的角拼凑成所求问题中的
角,可使用诱导公式.【解析】1.选A.原式= 2.由sin α+cos β=1与cos α+sin β=0分别平方相
加得sin2α+2sin αcos β+cos2β+cos2α+
2cos αsin β+sin2 β=1,即2+2sin αcos β+2cos αsin β=1,所以sin(α
+β)=- .
答案:- 3.因为0<α< +α<π,- -β
<0,
又已知sin
所以cos 所以cos(α+β)=
答案:- 【素养·探】
本例1考查利用两角和与差的正弦公式解决给角求值问
题,突出考查了数学抽象与数学运算的核心素养.若本
例1变形为下式,试求值.
的值是 ( )【解析】选A.原式= 角度2 求角与求点的坐标问题
【典例】1.已知α,β均为锐角,且sin α= ,cos β
= ,则α-β=________.?
2.已知向量 , 将向量 绕原点O顺时针旋转
60°到 的位置,则点A′的坐标为________.?【思维·引】
1.先由已知的三角函数值,选择适当的三角函数名求出所求角的三角函数值,再由已知角的范围,确定所求角的值.
2.利用向量的几何意义、三角函数的定义、两角差的正余弦公式解答.【解析】1.因为α,β均为锐角,且sin α= ,cos β
= ,
所以cos α= ,sin β=
所以sin (α-β)=sin αcos β-cos αsin β=又因为α,β均为锐角,所以- <α-β< ,故α-
β=- .
答案:- 2.如图,设A′ , ∠xOA=α, 所以∠xOA′=α-60°,则 =13,所以cos α= ,sin α= ,
因此x=13cos
同理y= ,所以A′
答案: 【类题·通】
1.解决给角求值问题的策略
(1)对于非特殊角的三角函数式求值问题,一定要本着先整体后局部的基本原则,如果整体符合三角公式的形式,则整体变形,否则进行各局部的变形.(2)解决三角函数的给值求值问题的关键是寻求“已知角”与“所求角”之间的关系,用“已知角”表示“所求角”.2.解决给值求角问题的一般思路
(1)确定角的范围;
(2)求角的正弦或余弦值;
(3)根据角的范围写出要求的角. 【习练·破】
1.已知cos (α为锐角),则sin α= ( )【解析】选D.因为α∈
所以α+
2.已知α,β为锐角,cos α= ,sin(α+β)= ,
则β=________.?【解析】因为α为锐角,且cos α= ,
所以sin α=
又α,β为锐角,所以α+β∈(0,π).
又sin(α+β)=
+sin(α+β)sin α
=
又β为锐角,所以β=
答案: 【加练·固】
1.化简下列各式:【解析】2.在△ABC中,3sin A+4cos B=6,3cos A+4sin B=1,则C的大小为 ( )【解析】选A.由已知可得(3sin A+4cos B)2+(3cos A+
4sin B)2=62+12,即9+16+24sin(A+B)=37.所以sin(A+B)
= .所以在△ABC中,sin C= ,所以C= 或C= .
又1-3cos A=4sin B>0,所以cos A< .
又 ,所以A> ,所以C< ,
所以C= 不符合题意,所以C= .类型二 两角和与差的正切公式的应用
【典例】1.计算 =________.?
2.tan 72°-tan 42°- tan 72°tan 42°=
________.?3.如图,在平面直角坐标系xOy中,以
Ox轴为始边作两个锐角α,β,它们的
终边分别与单位圆交于A,B两点.已知
A,B的横坐标分别为 .求:
(1)tan(α+β)的值;(2)α+2β的值. 世纪金榜导学号【思维·引】1.先用“tan45°=1”替换,再利用两角和的正切公式求值.
2.利用两角差的正切公式的变形公式解决.
3.(1)由三角函数的定义得出角α,β的正弦、余弦值,求出它们的正切值,利用两角和的正切公式解决.
(2)由α+2β=(α+β)+β,利用两角和的正切公式解决.【解析】1.原式= tan(45°
+15°)= tan 60°=1.
答案:12.原式=tan(72°-42°)(1+tan 72°·tan 42°)-
tan 72°tan 42°=tan 30°(1+tan 72°tan 42°)
-tan 30°tan 72°tan 42°=tan 30°= .
答案: 3.(1)由已知条件及三角函数的定义可知,
cos α= .因为α为锐角,故sin α>0,
从而sin α=
同理可得sin β= .因此tan α=7,tan β= .即tan(α+β)= =-3.(2)tan(α+2β)=tan[(α+β)+β]= =-1.
又0<α< ,0<β< ,故0<α+2β<
从而由tan(α+2β)=-1得α+2β= π.【内化·悟】
若已知条件中有角的正切值,一般的解决思路是什么?
提示:(1)切化弦,利用和差的正弦、余弦公式;(2)直接利用和差的正切公式.【类题·通】
1.公式Tα+β,Tα-β 应用的解题策略
(1)公式Tα+β,Tα-β有tan α·tan β,tan α+tan β(或tan α
-tan β),tan(α+β)(或tan(α-β)).三者知二可求出第三个;
(2)化简过程中注意“1”与“tan ”,“ ”与“tan ”
等特殊数与特殊角的函数值之间的转化.2.解决给值求角问题的选择原则
(1)已知正切函数值,选正切函数;
(2)已知正余弦函数值,选正弦或余弦函数,若角的范围是 ,
选正弦或余弦函数均可;若角的范围是(0,π),选余弦较好;若角
的范围是 ,选正弦较好.【习练·破】
1.求值:(1) 【解析】
(1)
(2)原式= =tan(45°+75°)=tan 120°
=- .2.已知tan(α-β)= ,tan β=- ,且α,β∈(-π,
0),求2α-β的值.【解析】因为α=(α-β)+β,tan(α-β)= ,tan β
=- ,α,β∈(-π,0),所以tan α=tan[(α-β)+β]
.又2α-β=α+(α-β),所以tan(2α-β)=tan[α+(α-β)]
=
而tan α= >0,tan β=- <0,α,β∈(-π,0),
则α∈ ,所以α-β∈(-π,0),而tan(α-β)= >0,则α-β∈
结合α∈ ,则有2α-β∈(-2π,-π),
所以2α-β=- .【加练·固】
1.tan 10°tan 20°+ (tan 10°+tan 20°)= ( ) 【解析】选B.原式=tan 10°tan 20°+ (1-
tan 10°tan 20°)·tan(10°+20°)=
tan 10°tan 20°+1-tan 10°tan 20°=1.2.在△ABC中,C=120°,tan A+tan B= ,则
tan Atan B的值为 ( )【解析】选B.因为C=120°,所以A+B=60°,
所以tan (A+B)=
因为tan A+tan B= ,
所以tan A+tan B= (1-tan A·tan B)= ,
解得tan A·tan B= .3.已知α,β,γ都是锐角,且tan α= ,tan β= ,
tan γ= ,则α+β+γ=________.?【解析】因为tan(α+β)=
tan(α+β+γ)= =1,因为tan α= ,且α为锐角,
所以0<α< ,同理0<β< ,0<γ< ,
所以0<α+β+γ< ,所以α+β+γ= .
答案: 类型三 辅助角公式的应用
【典例】1.cos α- sin α化简的结果可以是 ( ) 2.若函数f(x)=5cos x+12sin x在x=θ时取得最小值,
则cos θ等于 世纪金榜导学号( )【思维·引】利用辅助角公式进行变形.【解析】1.选B.cos α- sin α=
2.选B.f(x)=5cos x+12sin x
=
其中sin α= ,cos α= ,
由题意知θ+α=2kπ- (k∈Z)得θ=2kπ- -
α(k∈Z),所以 【内化·悟】
形如 sin α±cos α的式子通常如何变形?
提示: sin α±cos α=2 【类题·通】
把形如y=asin x+bcos x的式子化为y= sin(x+
φ),可进一步研究函数的周期性、单调性、最值与对
称性.【习练·破】
1.函数f(x)=sin x-cos x,x∈ 的最小值为( )
A.-2 B.- C.- D.-1【解析】选D.f(x)= ,因为0≤x≤ ,
所以- ,-
所以f(x)的最小值为-1.2.已知 的值为 ( ) 【解析】选B. 【加练·固】
1.(2018·全国卷Ⅱ)若f(x)=cos x-sin x在[-a,a]上
是减函数,则a的最大值是 ( )【解析】选A.f(x)=cos x-sin x=
上单调递减,所以[-a,a]?
故-a≥- 且a≤ ,解得0
φ)
则sin(a-φ)=±1,
所以a-φ=kπ+ ,k∈Z,
即a=kπ+ +φ,k∈Z,而tan φ= 且0<φ< ,
所以 <φ< ,
所以kπ+
