新教材人教B版数学必修第三册课件:8.2.4 三角恒等变换的应用(二)(48张PPT)
文档属性
| 名称 | 新教材人教B版数学必修第三册课件:8.2.4 三角恒等变换的应用(二)(48张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 00:00:00 | ||
图片预览





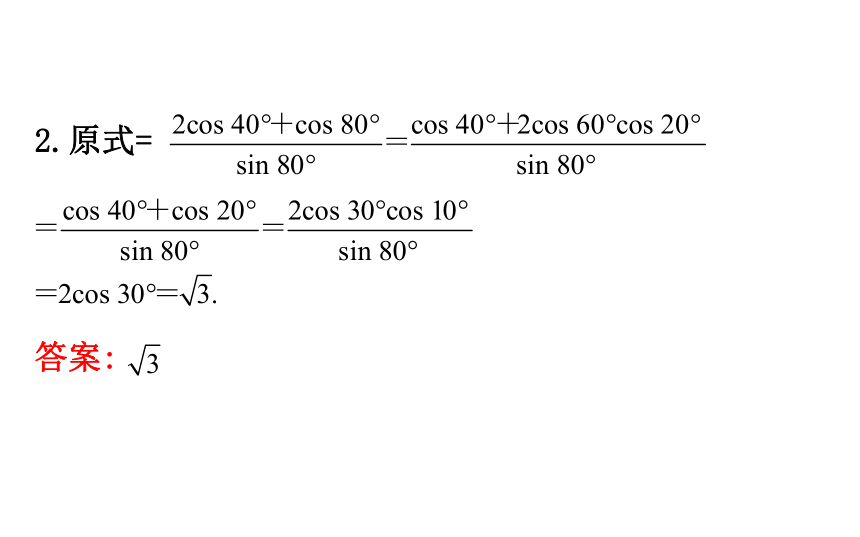

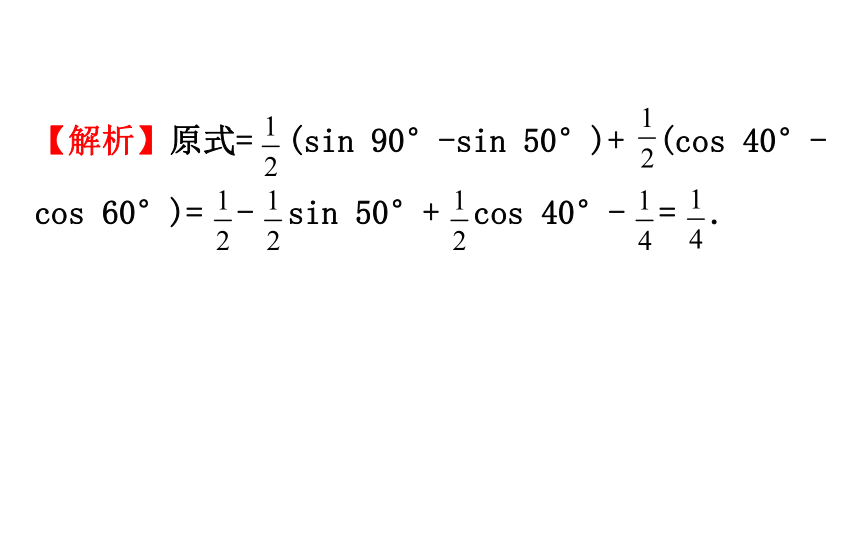




文档简介
课件48张PPT。8.2.4 三角恒等变换的应用(二)类型一 利用积化和差、和差化积公式化简求值、证明
角度1 利用积化和差、和差化积公式化简求值
【典例】1.在△ABC中,若sin Asin B=cos2 ,则△ABC是 ( )
A.等边三角形 B.等腰三角形
C.不等边三角形 D.直角三角形2. =________.?【思维·引】利用积化和差与和差化积公式化简、求值.【解析】1.选B.由已知得,
[cos(A-B)-cos(A+B)]= (1+cos C),
又A+B=π-C,所以cos(A-B)-cos(π-C)=1+cos C,
所以cos(A-B)=1,又-π所以A=B,故三角形为等腰三角形.2.原式=
答案: 【素养·探】
本题考查三角函数式的化简求值问题,同时考查数学运算与逻辑推理的核心素养.
若把本例2改为:
sin 20°cos 70°+sin 10°sin 50°,试求值.【解析】原式= (sin 90°-sin 50°)+ (cos 40°-
cos 60°)= - sin 50°+ cos 40°- = .角度2 利用积化和差、和差化积公式证明恒等式
【典例】在△ABC中,求证:
sin 2A+sin 2B+sin 2C=4sin Asin Bsin C.【思维·引】利用和差化积公式变形,直至两边相等.【证明】左边=sin 2A+sin 2B+sin 2C
=2sin cos +sin 2C
=2sin(A+B)cos(A-B)-2sin(A+B)·cos(A+B)
=2sin C[cos(A-B)-cos(A+B)]
=2sin C·(-2)sin
=4sin Asin Bsin C=右边.所以原等式成立.【类题·通】
(1)套用和差化积公式的关键是记准、记牢公式,为了能够把三角函数式化为积的形式,有时需要把常数首先化为某个角的三角函数,然后再化积,有时函数不同名,要先化为同名再化积,化积的结果能求值则尽量求出值来.(2)在运用积化和差求值时,尽量出现特殊角,同时注意互余角、互补角的三角函数间的关系.【习练·破】
(1)求值:cos 20°+cos 60°+cos 100°+cos 140°.
(2)已知A+B+C=π,求证:sin A+sin B-sin C= 【解析】(1)原式=cos 20°+ +(cos 100°+
cos 140°)=cos 20°+ +2cos 120°cos 20°
=cos 20°+ -cos 20°= .(2)因为左边=sin(B+C)+2sin
=2sin
=2cos
=2cos =右边.所以原等
式成立.类型二 利用积化和差、和差化积公式解决三角函数性
质问题
【典例】已知f(x)=- ,x∈(0,π).
(1)将f(x)表示成cos x的多项式.
(2)求f(x)的最小值.【思维·引】(1)利用积化和差、和差化积公式逐步化简,直至将f(x)表示成cos x的多项式.
(2)根据化简结果灵活选择求最值的方法.【解析】(1)f(x)=
=cos 2x+cos x=2cos2x+cos x-1.
(2)因为f(x)=2(cos x+ )2- ,且-1所以当cos x=- 时,f(x)取最小值- .【类题·通】
(1)利用积化和差、和差化积公式,一定要清楚这些公式的形式特征,理解公式间的关系.(2)求解三角函数的值域(最值)常见到的类型:
①形如y=asin x+bcos x+c的三角函数化为y=Asin(ωx+φ)+c或y=Acos(ωx+φ)+c的形式,再求值域(最值);
②形如y=asin2x+bsin x+c或y=acos2x+bcos x+c的三角函数,可先设sin x=t或cos x=t,化为关于t的二次函数求值域(最值).【习练·破】
1.函数f(x)=sin 的周期是 ( )
A. B.π C.2π D.4π【解析】选A.因为f(x)=
所以T= .2.函数y=cos 的最大值是________.?【解析】y=cos
所以ymax= .
答案: 类型三 三角恒等变换中角的变换问题
【典例】1.求值:sin(θ+75°)+cos(θ+45°)-
cos(θ+15°)=________.?
2.求值: =________.?3.已知tan(α+β)=λtan(α-β),其中λ≠1,求证:
. 世纪金榜导学号【思维·引】1.寻找角之间的关系,可令α=θ+15°,
则原式可转换为sin(α+60°)+cos(α+30°)-
cos α.
2.看到正切,想到将正切转化为正、余弦.
3.因为2α=(α+β)+(α-β),2β=(α+β)-(α-β),
把“未知”角转化为两个“已知”角的代数和,然后求解.【解析】1.令α=θ+15°,
则原式=sin(α+60°)+cos(α+30°)- cos α
= sin α+ cos α+ cos α- sin α-
cos α=0.
答案:0
答案:- 【内化·悟】
1.当求式中既含有正弦、余弦,又含有正切时,我们通常怎样解决?提示:利用同角的基本三角函数关系式tan α= 将
正切化为正弦和余弦,即“切化弦”,旨在减少三角函
数名称,转化为正弦、余弦的恒等变换.2.当已知角与未知角不同时,我们通常如何处理?
提示:通过角的变换(拆并角)找到已知角与未知角之间的联系,使公式顺利运用.【类题·通】
角的三种变换
(1)常见的配角变换.
α=2· ,α=(α+β)-β,α=β-(β-α),α= [(α
+β)+(α-β)],β= [(α+β)-(α-β)], (2)辅助角变换.
asin x+bcos x= sin(x+φ),其中tan φ=
(3)注意常值的代换.
用某些三角函数值代替某些常数,使之代换后能用相关
公式,如1=sin2α+cos2α,1=sin 90°, =sin 30°,
=cos 30°等.【习练·破】
1. =________.?【解析】原式=
答案:42.已知sin α=4sin(α+β),α+β≠kπ+ ,k∈Z,
求证:tan(α+β)= 【证明】因为sin α=4sin(α+β),
所以sin[(α+β)-β]=4sin(α+β),
所以sin(α+β)cos β-cos(α+β)sin β=4sin(α
+β).
所以(cos β-4)sin(α+β)=sin βcos(α+β),因为α+β≠kπ+ ,k∈Z,【加练·固】
-tan 20°= ( )【解析】选C.原式= 类型四 三角恒等变换在实际问题中的应用
实际问题情境
如图,某工匠要将一块圆心角为
120°,半径为20 cm的扇形铁片
裁成一块面积最大的矩形,现有
两种裁法:①让矩形一边在扇形的一半径OA上(如图①),②让矩形
一边与弦AB平行(如图②),请问该工匠应采用哪种裁法?并求出
这个矩形面积的最大值. 转化模板
1. —由题意可建立三角函数模型求解.
2. —如题干图①设∠MON=θ,如题干图②设∠MON=α.
3. —在题干图①中,求出矩形面积S1的最大值,在题
干图②中,求出矩形面积S2的最大值,比较大小即可.4. —在题干图①中,MN=20sin θ,ON=20cos θ,
所以S1=ON·NM=400sin θcos θ=200sin 2θ,
所以当sin 2θ=1,即θ=45°时,(S1)max=200 cm2.
在题干图②中,MQ=40sin(60°-α),MN= sin α,
所以S2= [cos(2α-60°)-cos 60°],当cos(2α-60°)=1,即2α-60°=0,
即α=30°时,(S2)max= cm2.因为 >200,
所以用题干图②这种裁法得到的矩形的面积最大,为
cm2.
5. —该工匠应采用题干图②这种裁法,这个矩形面
积的最大值为 cm2.
角度1 利用积化和差、和差化积公式化简求值
【典例】1.在△ABC中,若sin Asin B=cos2 ,则△ABC是 ( )
A.等边三角形 B.等腰三角形
C.不等边三角形 D.直角三角形2. =________.?【思维·引】利用积化和差与和差化积公式化简、求值.【解析】1.选B.由已知得,
[cos(A-B)-cos(A+B)]= (1+cos C),
又A+B=π-C,所以cos(A-B)-cos(π-C)=1+cos C,
所以cos(A-B)=1,又-π
答案: 【素养·探】
本题考查三角函数式的化简求值问题,同时考查数学运算与逻辑推理的核心素养.
若把本例2改为:
sin 20°cos 70°+sin 10°sin 50°,试求值.【解析】原式= (sin 90°-sin 50°)+ (cos 40°-
cos 60°)= - sin 50°+ cos 40°- = .角度2 利用积化和差、和差化积公式证明恒等式
【典例】在△ABC中,求证:
sin 2A+sin 2B+sin 2C=4sin Asin Bsin C.【思维·引】利用和差化积公式变形,直至两边相等.【证明】左边=sin 2A+sin 2B+sin 2C
=2sin cos +sin 2C
=2sin(A+B)cos(A-B)-2sin(A+B)·cos(A+B)
=2sin C[cos(A-B)-cos(A+B)]
=2sin C·(-2)sin
=4sin Asin Bsin C=右边.所以原等式成立.【类题·通】
(1)套用和差化积公式的关键是记准、记牢公式,为了能够把三角函数式化为积的形式,有时需要把常数首先化为某个角的三角函数,然后再化积,有时函数不同名,要先化为同名再化积,化积的结果能求值则尽量求出值来.(2)在运用积化和差求值时,尽量出现特殊角,同时注意互余角、互补角的三角函数间的关系.【习练·破】
(1)求值:cos 20°+cos 60°+cos 100°+cos 140°.
(2)已知A+B+C=π,求证:sin A+sin B-sin C= 【解析】(1)原式=cos 20°+ +(cos 100°+
cos 140°)=cos 20°+ +2cos 120°cos 20°
=cos 20°+ -cos 20°= .(2)因为左边=sin(B+C)+2sin
=2sin
=2cos
=2cos =右边.所以原等
式成立.类型二 利用积化和差、和差化积公式解决三角函数性
质问题
【典例】已知f(x)=- ,x∈(0,π).
(1)将f(x)表示成cos x的多项式.
(2)求f(x)的最小值.【思维·引】(1)利用积化和差、和差化积公式逐步化简,直至将f(x)表示成cos x的多项式.
(2)根据化简结果灵活选择求最值的方法.【解析】(1)f(x)=
=cos 2x+cos x=2cos2x+cos x-1.
(2)因为f(x)=2(cos x+ )2- ,且-1
(1)利用积化和差、和差化积公式,一定要清楚这些公式的形式特征,理解公式间的关系.(2)求解三角函数的值域(最值)常见到的类型:
①形如y=asin x+bcos x+c的三角函数化为y=Asin(ωx+φ)+c或y=Acos(ωx+φ)+c的形式,再求值域(最值);
②形如y=asin2x+bsin x+c或y=acos2x+bcos x+c的三角函数,可先设sin x=t或cos x=t,化为关于t的二次函数求值域(最值).【习练·破】
1.函数f(x)=sin 的周期是 ( )
A. B.π C.2π D.4π【解析】选A.因为f(x)=
所以T= .2.函数y=cos 的最大值是________.?【解析】y=cos
所以ymax= .
答案: 类型三 三角恒等变换中角的变换问题
【典例】1.求值:sin(θ+75°)+cos(θ+45°)-
cos(θ+15°)=________.?
2.求值: =________.?3.已知tan(α+β)=λtan(α-β),其中λ≠1,求证:
. 世纪金榜导学号【思维·引】1.寻找角之间的关系,可令α=θ+15°,
则原式可转换为sin(α+60°)+cos(α+30°)-
cos α.
2.看到正切,想到将正切转化为正、余弦.
3.因为2α=(α+β)+(α-β),2β=(α+β)-(α-β),
把“未知”角转化为两个“已知”角的代数和,然后求解.【解析】1.令α=θ+15°,
则原式=sin(α+60°)+cos(α+30°)- cos α
= sin α+ cos α+ cos α- sin α-
cos α=0.
答案:0
答案:- 【内化·悟】
1.当求式中既含有正弦、余弦,又含有正切时,我们通常怎样解决?提示:利用同角的基本三角函数关系式tan α= 将
正切化为正弦和余弦,即“切化弦”,旨在减少三角函
数名称,转化为正弦、余弦的恒等变换.2.当已知角与未知角不同时,我们通常如何处理?
提示:通过角的变换(拆并角)找到已知角与未知角之间的联系,使公式顺利运用.【类题·通】
角的三种变换
(1)常见的配角变换.
α=2· ,α=(α+β)-β,α=β-(β-α),α= [(α
+β)+(α-β)],β= [(α+β)-(α-β)], (2)辅助角变换.
asin x+bcos x= sin(x+φ),其中tan φ=
(3)注意常值的代换.
用某些三角函数值代替某些常数,使之代换后能用相关
公式,如1=sin2α+cos2α,1=sin 90°, =sin 30°,
=cos 30°等.【习练·破】
1. =________.?【解析】原式=
答案:42.已知sin α=4sin(α+β),α+β≠kπ+ ,k∈Z,
求证:tan(α+β)= 【证明】因为sin α=4sin(α+β),
所以sin[(α+β)-β]=4sin(α+β),
所以sin(α+β)cos β-cos(α+β)sin β=4sin(α
+β).
所以(cos β-4)sin(α+β)=sin βcos(α+β),因为α+β≠kπ+ ,k∈Z,【加练·固】
-tan 20°= ( )【解析】选C.原式= 类型四 三角恒等变换在实际问题中的应用
实际问题情境
如图,某工匠要将一块圆心角为
120°,半径为20 cm的扇形铁片
裁成一块面积最大的矩形,现有
两种裁法:①让矩形一边在扇形的一半径OA上(如图①),②让矩形
一边与弦AB平行(如图②),请问该工匠应采用哪种裁法?并求出
这个矩形面积的最大值. 转化模板
1. —由题意可建立三角函数模型求解.
2. —如题干图①设∠MON=θ,如题干图②设∠MON=α.
3. —在题干图①中,求出矩形面积S1的最大值,在题
干图②中,求出矩形面积S2的最大值,比较大小即可.4. —在题干图①中,MN=20sin θ,ON=20cos θ,
所以S1=ON·NM=400sin θcos θ=200sin 2θ,
所以当sin 2θ=1,即θ=45°时,(S1)max=200 cm2.
在题干图②中,MQ=40sin(60°-α),MN= sin α,
所以S2= [cos(2α-60°)-cos 60°],当cos(2α-60°)=1,即2α-60°=0,
即α=30°时,(S2)max= cm2.因为 >200,
所以用题干图②这种裁法得到的矩形的面积最大,为
cm2.
5. —该工匠应采用题干图②这种裁法,这个矩形面
积的最大值为 cm2.
