青岛版数学五四制三年级下册第9单元《解决问题》知识点解析及练习(含答案)
文档属性
| 名称 | 青岛版数学五四制三年级下册第9单元《解决问题》知识点解析及练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 61.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-21 00:00:00 | ||
图片预览


文档简介
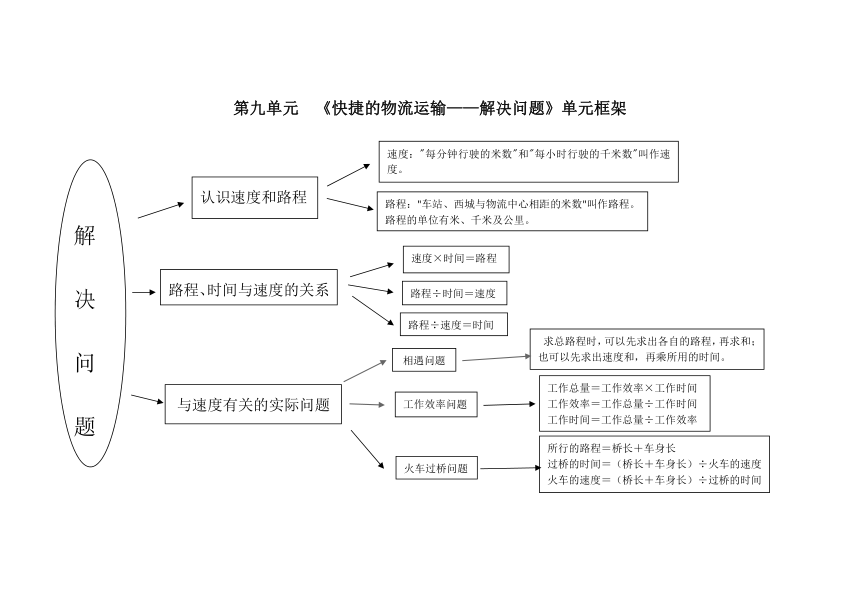
第九单元 《快捷的物流运输——解决问题》单元框架
解
决
问
题
信息窗——解决问题
一、知识点解读
1. 路程、时间与速度的关系(理解识记)
知识点:路程、时间与速度的关系:速度×时间=路程 路程÷时间=速度 路程÷速度=时间
教学要求:借助生活实例,让学生知道速度的意义写法和读法,理解路程、时间与速度的概念,能自行归纳出:速度×时间=路程,并能根据这一数量关系式得出其他的数量关系式:路程÷时间=速度,路程÷速度=时间,会利用公式及它们之间的关系。
2. 运算的应用(掌握运用)
知识点:根据路程、速度与时间的关系解决生活中的相遇问题。
教学要求:将路程、速度与时间的关系运用到日常教学之中。在课中要让学生在例题的学习中体会解决问题的分析方法(从问题出发分析或从条件出发分析),学会运用模拟演示和划线段图等方法理解数量关系,初步构建相遇问题的数学模型,学生能自行总结出:求总路程时,可以先求出各自的路程,再求和;也可以先求出速度和,再乘所用的时间。
二、知识拓展
1. 追及问题
追击问题是指两个物体同向运动,后一个速度快的物体追前一个速度慢的物体的一种相遇问题,它们之间的关系式是“路程差÷速度差=追及时间”。
2. 工作效率问题
像“80字/分,300个/时,这样的叫做工作效率。用到的关系式是:工作总量=工作效率×工作时间,工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率。
3. 火车过桥问题
解决这种问题用分析法,由问题入手倒推到已知条件,注意:所行的路程=桥长+车身长,过桥的时间=(桥长+车身长)÷火车的速度,火车的速度=(桥长+车身长)÷过桥的时间。
三、知识点训练
基础训练
1. 一辆小汽车,在高速公路上2小时行驶了240千米,那么它平均每分钟行驶
了( )千米。
2. 汽车在公路上行驶了420千米,用了6小时,它的速度是( )。
A. 70千米 B. 70千米/时 C.70千米时
3. 甲车平均每秒行驶15米,乙车6分钟行驶3600米,哪辆车的速度快?
能力提升
1. 甲地到乙地的铁路长约2313千米。一列火车以108千米/时的速度从甲地开往乙地,20小时能到吗?
2. 小强和小静在环形跑道上跑步,两人从同一地点同时出发反向而行。小强每秒跑6米,小静每秒跑4米,经过40秒两人相遇,环形跑道一圈长多少米?
3. 一辆轿车和一辆客车分别从A、B两地同时出发,相向而行,经过5小时,两车相遇,相遇后客车继续行驶,又经过7小时到达A地,已知轿车每小时行驶63千米,求A、B两地相距多少千米?
拓展应用
1. A、B两地相距240千米,甲、乙两车分别从A、B地两地同时出发,相向而行,3小时后相遇,甲车平均每小时行驶42千米,乙车平均每小时行驶多少千米?
2. 一辆轿车和一辆货车从甲城开往乙城,轿车每小时行驶80千米,货车每小时行驶50千米。货车开出3小时后,轿车从甲城出发,轿车开出几小时后能追上货车?
3. 甲乙两车同时从A地开往B地。甲车每小时行驶58千米,乙车每小时行驶42千米,甲车到达B地后立即返回,两车行驶6小时后第一次相遇,求A、B两地间的距离。
训练题参考答案及解析
基础训练
1. 2 2. B 3. 甲车快
能力提升
1. 108×20=2160(千米) 2160<2313 答:不能
2.(6+4)×40=400(米)
3. 63×5÷7=45(千米) 5+7=12(小时) 45×12=540(千米)
拓展应用
1. 240÷3=80(千米) 80-42=38(千米)
2. 分析:由题意知道,货车先行3小时,轿车出发时,两车之间已相距
(50×3)千米。当轿车出发后,两车同时行驶,每行驶1小时,轿车就追回(80-50)千米。货车先行的(50×3)千米中有几个(80-50)千米,需要几小
时追上。
列式为:50×3=150(千米) 80-50=30(千米)
150÷30=5(小时)
答:轿车开出5小时后能追上货车。
3. 分析:解决此题的关键是明确:第一次相遇时两车行驶的路程之和正好是A、B两地间距离的2倍。ss
列式为:(42+58)×6÷2=300(千米)
答:A、B两地间的距离是300千米。
解
决
问
题
信息窗——解决问题
一、知识点解读
1. 路程、时间与速度的关系(理解识记)
知识点:路程、时间与速度的关系:速度×时间=路程 路程÷时间=速度 路程÷速度=时间
教学要求:借助生活实例,让学生知道速度的意义写法和读法,理解路程、时间与速度的概念,能自行归纳出:速度×时间=路程,并能根据这一数量关系式得出其他的数量关系式:路程÷时间=速度,路程÷速度=时间,会利用公式及它们之间的关系。
2. 运算的应用(掌握运用)
知识点:根据路程、速度与时间的关系解决生活中的相遇问题。
教学要求:将路程、速度与时间的关系运用到日常教学之中。在课中要让学生在例题的学习中体会解决问题的分析方法(从问题出发分析或从条件出发分析),学会运用模拟演示和划线段图等方法理解数量关系,初步构建相遇问题的数学模型,学生能自行总结出:求总路程时,可以先求出各自的路程,再求和;也可以先求出速度和,再乘所用的时间。
二、知识拓展
1. 追及问题
追击问题是指两个物体同向运动,后一个速度快的物体追前一个速度慢的物体的一种相遇问题,它们之间的关系式是“路程差÷速度差=追及时间”。
2. 工作效率问题
像“80字/分,300个/时,这样的叫做工作效率。用到的关系式是:工作总量=工作效率×工作时间,工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率。
3. 火车过桥问题
解决这种问题用分析法,由问题入手倒推到已知条件,注意:所行的路程=桥长+车身长,过桥的时间=(桥长+车身长)÷火车的速度,火车的速度=(桥长+车身长)÷过桥的时间。
三、知识点训练
基础训练
1. 一辆小汽车,在高速公路上2小时行驶了240千米,那么它平均每分钟行驶
了( )千米。
2. 汽车在公路上行驶了420千米,用了6小时,它的速度是( )。
A. 70千米 B. 70千米/时 C.70千米时
3. 甲车平均每秒行驶15米,乙车6分钟行驶3600米,哪辆车的速度快?
能力提升
1. 甲地到乙地的铁路长约2313千米。一列火车以108千米/时的速度从甲地开往乙地,20小时能到吗?
2. 小强和小静在环形跑道上跑步,两人从同一地点同时出发反向而行。小强每秒跑6米,小静每秒跑4米,经过40秒两人相遇,环形跑道一圈长多少米?
3. 一辆轿车和一辆客车分别从A、B两地同时出发,相向而行,经过5小时,两车相遇,相遇后客车继续行驶,又经过7小时到达A地,已知轿车每小时行驶63千米,求A、B两地相距多少千米?
拓展应用
1. A、B两地相距240千米,甲、乙两车分别从A、B地两地同时出发,相向而行,3小时后相遇,甲车平均每小时行驶42千米,乙车平均每小时行驶多少千米?
2. 一辆轿车和一辆货车从甲城开往乙城,轿车每小时行驶80千米,货车每小时行驶50千米。货车开出3小时后,轿车从甲城出发,轿车开出几小时后能追上货车?
3. 甲乙两车同时从A地开往B地。甲车每小时行驶58千米,乙车每小时行驶42千米,甲车到达B地后立即返回,两车行驶6小时后第一次相遇,求A、B两地间的距离。
训练题参考答案及解析
基础训练
1. 2 2. B 3. 甲车快
能力提升
1. 108×20=2160(千米) 2160<2313 答:不能
2.(6+4)×40=400(米)
3. 63×5÷7=45(千米) 5+7=12(小时) 45×12=540(千米)
拓展应用
1. 240÷3=80(千米) 80-42=38(千米)
2. 分析:由题意知道,货车先行3小时,轿车出发时,两车之间已相距
(50×3)千米。当轿车出发后,两车同时行驶,每行驶1小时,轿车就追回(80-50)千米。货车先行的(50×3)千米中有几个(80-50)千米,需要几小
时追上。
列式为:50×3=150(千米) 80-50=30(千米)
150÷30=5(小时)
答:轿车开出5小时后能追上货车。
3. 分析:解决此题的关键是明确:第一次相遇时两车行驶的路程之和正好是A、B两地间距离的2倍。ss
列式为:(42+58)×6÷2=300(千米)
答:A、B两地间的距离是300千米。
