2019_2020学年高中数学第二章平面向量章末小结与测评课件新人教A版必修4(共24张PPT)
文档属性
| 名称 | 2019_2020学年高中数学第二章平面向量章末小结与测评课件新人教A版必修4(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 11:04:42 | ||
图片预览




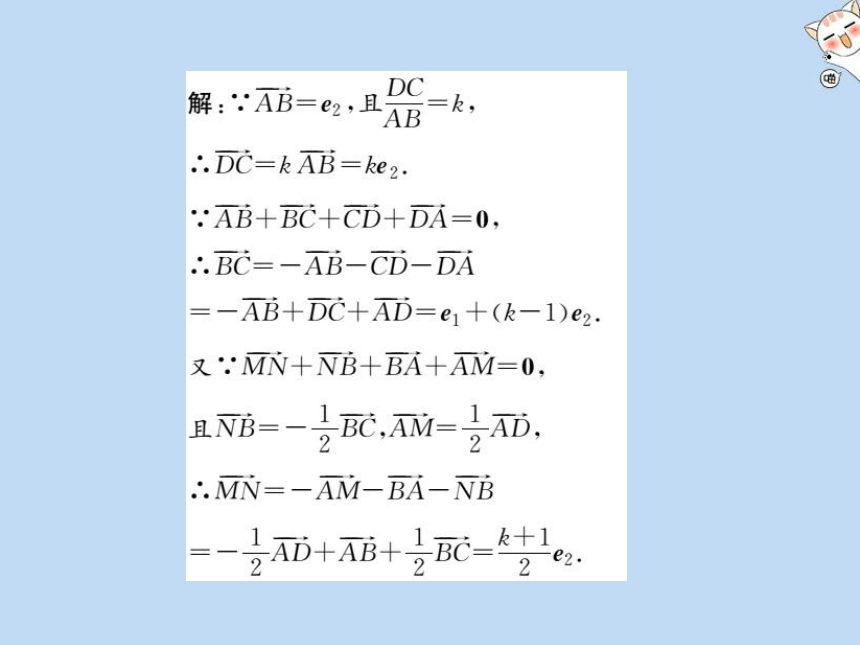


文档简介
(共24张PPT)
章末小结与测评
贯穿所学知识·评价学习效果
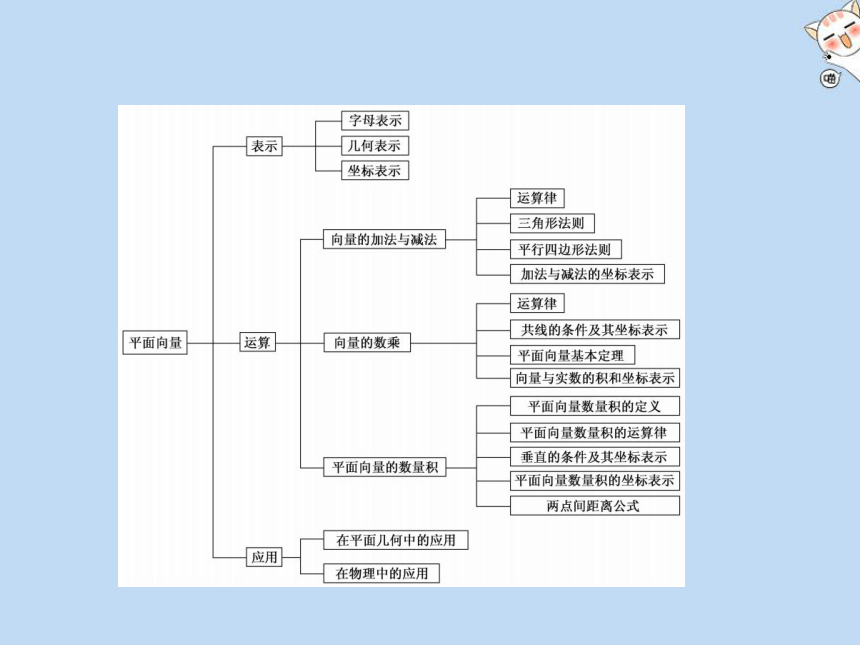
主干知识·建体系
zH∪ GANZHISH
字母表示
表
几何表示
L坐标表示
[运算律
三角形法则
‖向量的加法与减法
平行四边形法则
七加法与减法的坐标表示
运算律
共线的条件及其坐标表示
平面向量
运算
[向量的数乘
平面向量基本定理
向量与实数的积和坐标表示
平面向量数量积的定义
平面向量数量积的运算律
垂直的条件及其坐标表示
平面向量的数量积
1[平面向量数量积的坐标表示
两点间距离公式
在平面几何中的应用
应用
在物理中的应用
考点
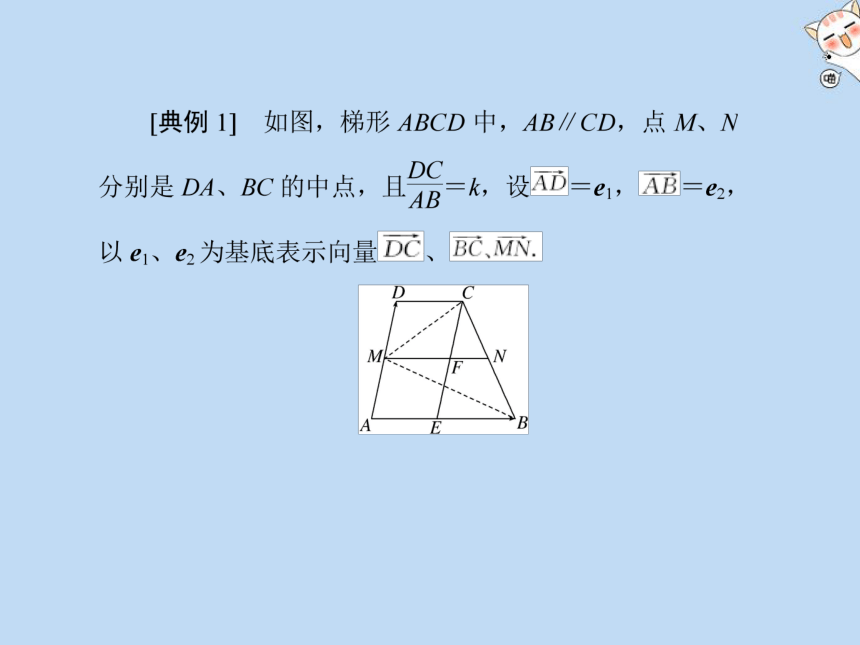
平面向量的线性运算
锁定高老·攻考点
S∪ ODINGGA○KA○
DC
解:∴AB=e2,且
k
AB
DC=kab=ke 2
∵AB+BC+CD+DA=0,
BC=-AB-CD-DA
AB+DC+AD=e,+(k-1)e
又∵MN+NB+BA+AM=0,
且NB=-1BC,AM=1AD
MN=-AM一BA-NB
k
DAD+AB+ obC=-o-e2
[对点训练]
1.如图,在△ABC中,AQ=QC,AR
AB,BQ与CR相交于点Ⅰ
Q
AI的延长线与边BC交于点P
(1)用AB和AC分别表示BQ和CR
(2)如果AI=AB+ABQ=AC+pCR,求实数A和g
的值
(3)确定点P在边BC上的位置
解:(1)由AQ=bAC,可得
BQ=BA+AQ=-AB+AC
又AR
aB.
所以CR=CA+AR=-AC+AB
2)+BQ=-AB-+AC, CR=-AC+AB
代入AI=AB+ABQ=AC+pCR,
则有AB+(-AB+。AC
=AC+ul-AC+AB
3
即(1-A)AB++AAC=、1
AB+(1
Ac
1-x=1
所以
解得
=1-
-5
(3)设BP=mBC,AP=nAI
由(2),知AI=÷AB+-AC,
所以BP=AP-AB=nAI-AB
n(不B+3不C)-万1=3xC+(3-1)B
m bc=mac-maB,
n
n
所以
解得
2n
353
所以BF=4BC,
BP
PC=2,P是边BC上靠近C的三等分点
考点二
平面向量的坐标运算
考点三
平面向量的数量积
解析:令OM|=x(0≤x≤2),
则|OA|=2-x
OA·(OB+OC)=OA·2OM
=2 OM cos 180
=2·(2-x)·x·(-1)=2(x2-2x)
=2(x-1)2-2(0≤x≤2),
当x=1时,即O为AM的中点时,
OA·(OB+OC)取最小值为-2
章末小结与测评
贯穿所学知识·评价学习效果
主干知识·建体系
zH∪ GANZHISH
字母表示
表
几何表示
L坐标表示
[运算律
三角形法则
‖向量的加法与减法
平行四边形法则
七加法与减法的坐标表示
运算律
共线的条件及其坐标表示
平面向量
运算
[向量的数乘
平面向量基本定理
向量与实数的积和坐标表示
平面向量数量积的定义
平面向量数量积的运算律
垂直的条件及其坐标表示
平面向量的数量积
1[平面向量数量积的坐标表示
两点间距离公式
在平面几何中的应用
应用
在物理中的应用
考点
平面向量的线性运算
锁定高老·攻考点
S∪ ODINGGA○KA○
DC
解:∴AB=e2,且
k
AB
DC=kab=ke 2
∵AB+BC+CD+DA=0,
BC=-AB-CD-DA
AB+DC+AD=e,+(k-1)e
又∵MN+NB+BA+AM=0,
且NB=-1BC,AM=1AD
MN=-AM一BA-NB
k
DAD+AB+ obC=-o-e2
[对点训练]
1.如图,在△ABC中,AQ=QC,AR
AB,BQ与CR相交于点Ⅰ
Q
AI的延长线与边BC交于点P
(1)用AB和AC分别表示BQ和CR
(2)如果AI=AB+ABQ=AC+pCR,求实数A和g
的值
(3)确定点P在边BC上的位置
解:(1)由AQ=bAC,可得
BQ=BA+AQ=-AB+AC
又AR
aB.
所以CR=CA+AR=-AC+AB
2)+BQ=-AB-+AC, CR=-AC+AB
代入AI=AB+ABQ=AC+pCR,
则有AB+(-AB+。AC
=AC+ul-AC+AB
3
即(1-A)AB++AAC=、1
AB+(1
Ac
1-x=1
所以
解得
=1-
-5
(3)设BP=mBC,AP=nAI
由(2),知AI=÷AB+-AC,
所以BP=AP-AB=nAI-AB
n(不B+3不C)-万1=3xC+(3-1)B
m bc=mac-maB,
n
n
所以
解得
2n
353
所以BF=4BC,
BP
PC=2,P是边BC上靠近C的三等分点
考点二
平面向量的坐标运算
考点三
平面向量的数量积
解析:令OM|=x(0≤x≤2),
则|OA|=2-x
OA·(OB+OC)=OA·2OM
=2 OM cos 180
=2·(2-x)·x·(-1)=2(x2-2x)
=2(x-1)2-2(0≤x≤2),
当x=1时,即O为AM的中点时,
OA·(OB+OC)取最小值为-2
