江西省上饶市“山江湖”协作体2019-2020学年高二上学期期中联考试题 数学(理) (统招班) word版含答案
文档属性
| 名称 | 江西省上饶市“山江湖”协作体2019-2020学年高二上学期期中联考试题 数学(理) (统招班) word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 593.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览


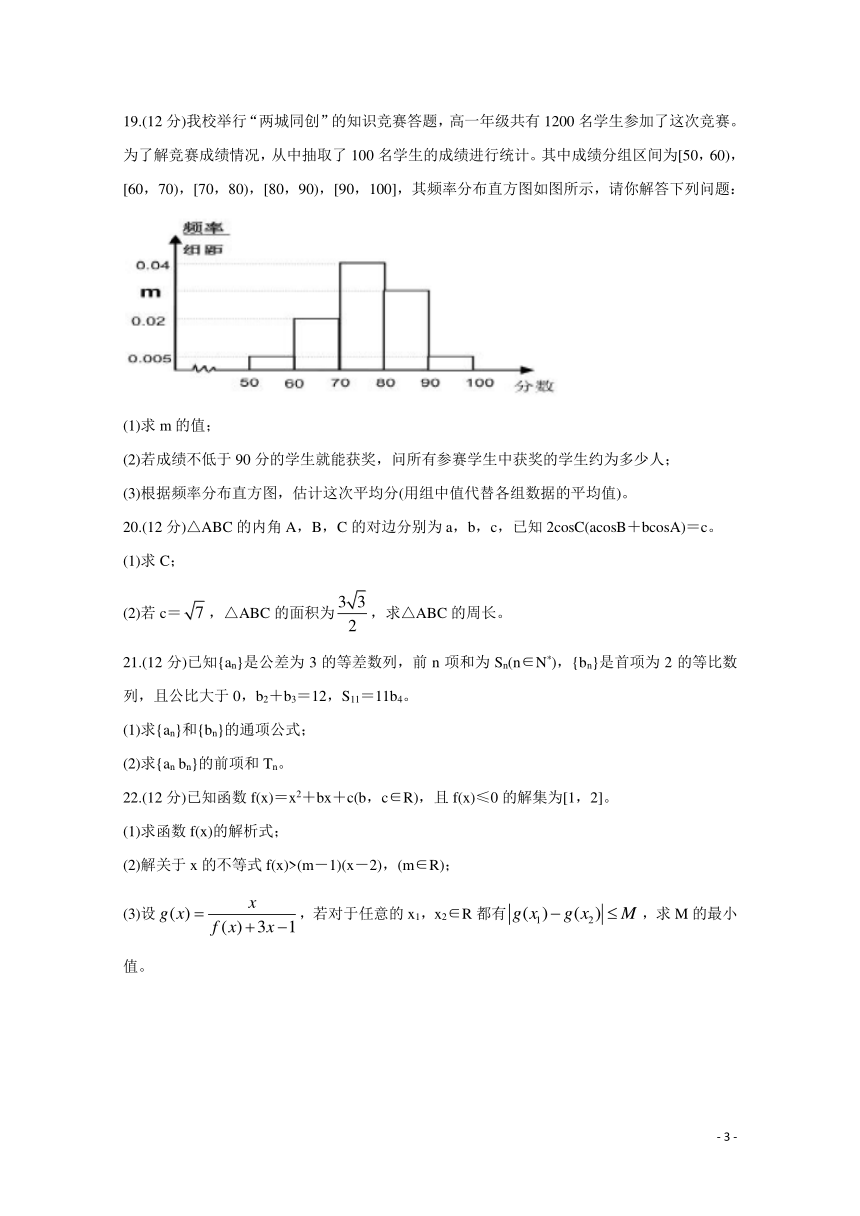

同课章节目录
