2020年湘教新版九年级上册数学《第5章 用样本推断总体》单元测试卷(解析版)
文档属性
| 名称 | 2020年湘教新版九年级上册数学《第5章 用样本推断总体》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 364.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-21 12:37:04 | ||
图片预览



文档简介
2020年湘教新版九年级上册数学《第5章 用样本推断总体》单元测试卷
一.选择题(共12小题)
1.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A.440 B.495 C.550 D.660
2.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.1000只 B.10000只 C.5000只 D.50000只
3.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
4.为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱动画节目的学生约有( )
A.500名 B.600名 C.700名 D.800名
5.2006年1月1日起,某市全面推行农村合作医疗,农民每年每人只拿出10元就可以享受合作医疗.某人住院费报销了805元,则花费了( )
住院费(元) 报销率(%)
不超过3000元部分 15
3000﹣4000部分 25
4000﹣5000部分 30
5000﹣10000部分 35
10000﹣20000部分 40
超过20000部分 45
A.3220 B.4183.33 C.4350 D.4500
6.下表选自北京师范大学出版社出版的《数学》课本(九年级下册).
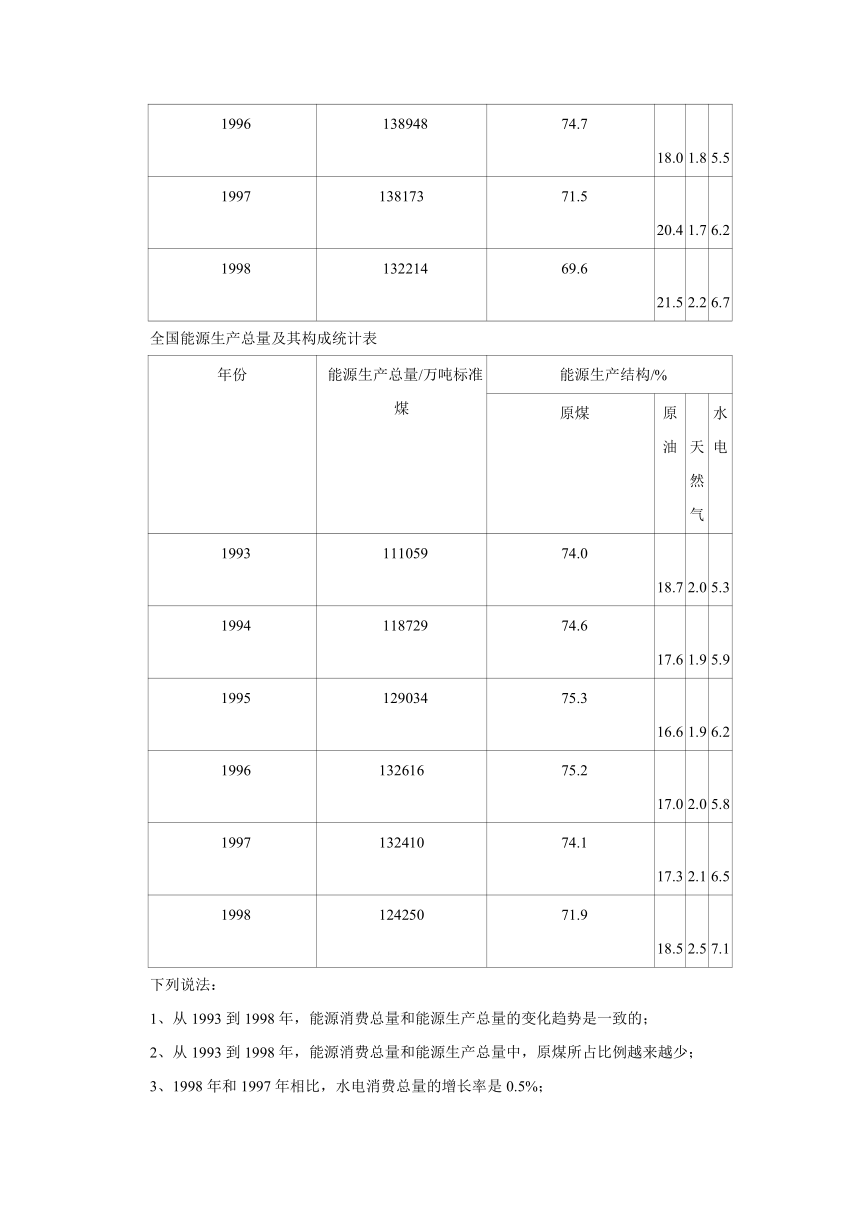
全国能源消费总量及其构成统计表
年份 能源消费总量/万吨标准煤 能源消费构成/%
原煤 原油 天然气 水电
1993 115993 74.7 18.2 1.9 5.2
1994 122737 75.0 17.4 1.9 5.7
1995 131176 74.6 17.5 1.8 6.1
1996 138948 74.7 18.0 1.8 5.5
1997 138173 71.5 20.4 1.7 6.2
1998 132214 69.6 21.5 2.2 6.7
全国能源生产总量及其构成统计表
年份 能源生产总量/万吨标准煤 能源生产结构/%
原煤 原油 天然气 水电
1993 111059 74.0 18.7 2.0 5.3
1994 118729 74.6 17.6 1.9 5.9
1995 129034 75.3 16.6 1.9 6.2
1996 132616 75.2 17.0 2.0 5.8
1997 132410 74.1 17.3 2.1 6.5
1998 124250 71.9 18.5 2.5 7.1
下列说法:
1、从1993到1998年,能源消费总量和能源生产总量的变化趋势是一致的;
2、从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例越来越少;
3、1998年和1997年相比,水电消费总量的增长率是0.5%;
4、从1993到1998年,能源生产中,天然气生产总量越来越多.
其中正确的是( )
A.①③ B.①④ C.③④ D.①②
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元) 300 280 260 220
入住率 65% 75% 85% 95%
A.300元 B.280元 C.260元 D.220元
8.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
项目人数级别 三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
A.3项 B.4项 C.5项 D.6项
9.要反映青岛市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.频数分布图 D.折线统计图
10.下列说法不正确的是( )
A.为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图
B.为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图
C.为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图
D.以上三种统计图都可以直接找到所需数目
11.为了记录一个病人的体温变化情况,应选择的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
12.空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )
A.折线图 B.条形图 C.直方图 D.扇形图
二.填空题(共8小题)
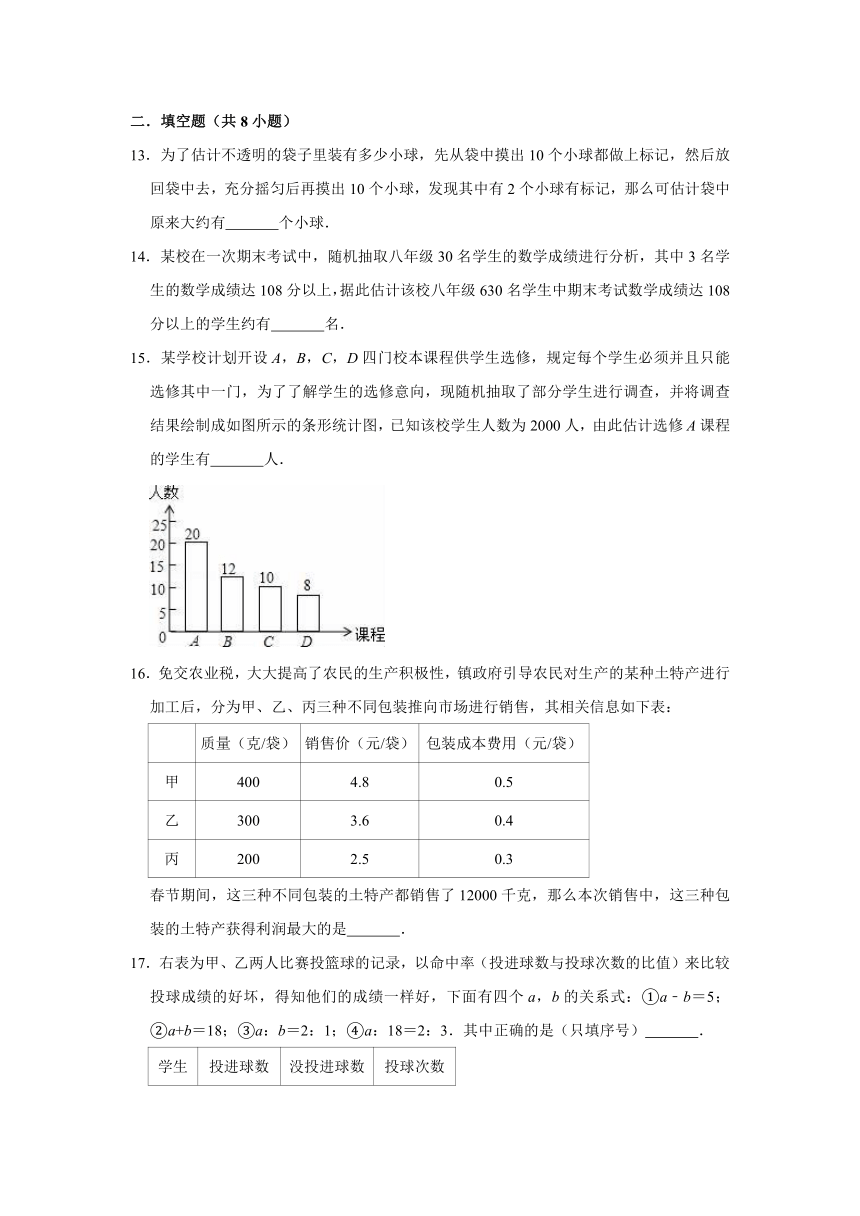
13.为了估计不透明的袋子里装有多少小球,先从袋中摸出10个小球都做上标记,然后放回袋中去,充分摇匀后再摸出10个小球,发现其中有2个小球有标记,那么可估计袋中原来大约有 个小球.
14.某校在一次期末考试中,随机抽取八年级30名学生的数学成绩进行分析,其中3名学生的数学成绩达108分以上,据此估计该校八年级630名学生中期末考试数学成绩达108分以上的学生约有 名.
15.某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有 人.
16.免交农业税,大大提高了农民的生产积极性,镇政府引导农民对生产的某种土特产进行加工后,分为甲、乙、丙三种不同包装推向市场进行销售,其相关信息如下表:
质量(克/袋) 销售价(元/袋) 包装成本费用(元/袋)
甲 400 4.8 0.5
乙 300 3.6 0.4
丙 200 2.5 0.3
春节期间,这三种不同包装的土特产都销售了12000千克,那么本次销售中,这三种包装的土特产获得利润最大的是 .
17.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a﹣b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号) .
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
18.某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.1 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有 人,视力为1.0的有 人,视力小于1.0的有 人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有 人,视力正常的人数占全班人数的 %;
(3)该班学生视力情况 (选填“好”“一般”“差”).
19.据统计,近几年全世界森林面积以每年约1700万公顷的速度消失,为了预测未来20年世界森林面积的变化趋势,可选用 统计图表示收集到的数据.
20.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共8小题)
21.某学校抽查了某班级某月10天的用电量,数据如下表(单位:度);
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是 ,中位数是 ,极差是 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
22.“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区10户居民的日用电量,数据如下:
用户序号 1 2 3 4 5 6 7 8 9 10
日用电量(度) 4.4 4.0 5.0 5.6 3.4 4.8 3.4 5.2 4.0 4.2
(1)求这组数据的极差和平均数;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
23.某公司为了了解公司每天的用电情况,抽查了某月10天全公司的用电数量,数据如下表(单位:度):
度数 90 100 102 110 116 120
天数 1 1 2 3 1 2
(1)求出上表中数据的众数和平均数;
(2)根据获得的数据,估计该公司本月的用电数量(按30天计算);若每度电的定价为0.5元,试估算本月的电费支出约多少元?
24.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1号 2号 3号 4号 5号 总分
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
25.某中学开展以“八荣八耻”为主题的社会主义荣辱观教育活动,举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 15
认真观察阅读统计表后,回答下列问题:
(1)请补充完成这个统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的“众数”是 ;
(3)手抄报作品与漫画作品的获奖人数分别是6人和3人,你认为“手抄报作品比漫画作品的获奖率高”这种说法是否正确,请说明你的理由.
26.我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
4 5 7 6 3 7 9 4 5 7
7 3 7 5 6 8 7 5 6 8
6 7 4 10 5 6 7 3 9 4
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
27.2007年12月31日,国务院办公厅关于限制生产销售使用塑料购物袋的通知要求:从2008年6月1日起,在全国范围内禁止生产,销售,使用厚度小于0.025毫米的塑料购物袋(以下简称超薄塑料购物袋).
2007年底,某校初四年级一班的同学到学校附近的农贸市场调查了这个市场里100家商户中的10家.这10家商户平均每天送出的超薄塑料购物袋数量分别为(单位:把):
4 5 3 8 5 7 5 6 3 4
(1)请分别写出这组数据的众数,中位数;
(2)如果要选择一种统计图来表示这10家商户送出的超薄塑料购物袋的情况,在条形统计图,折线统计图,扇形统计图中你会选择哪一个;
(3)已知一把超薄塑料购物袋有50个.通过对样本的计算,估计该农贸市场一年要送出多少个超薄塑料购物袋?(一年按350个营业日计算)结果用科学记数法表示.
28.2005年5月20日《成都商报》报道:四川第二家民营航空公司﹣﹣西部航空有限责任公司即将诞生,公司基地落户绵阳.组建该公司的投资公司及注册的投资资本如下表:
投资公司(简称) 海特投资 惠建立 三星通用航空 翔龙进出口 国瑞投资 银燕创新
投资成本(万元) 3000 3000 1500 1300 700 500
请回答下列问题:
(1)西部航空有限责任公司申请注册的资本为多少元?(用科学记数法表示)
(2)将上述统计表用一种合适的统计图来表示.
2020年湘教新版九年级上册数学《第5章 用样本推断总体》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A.440 B.495 C.550 D.660
【分析】根据记不清在扇形统计图中所占120°,在条形图中为30,得出总人数,根据(1)中所求总人数,即可求出调查的学生中“知道”的学生数,再利用样本估计总体的方法计算出答案即可.
【解答】解:调查的总人数:30÷=90,
知道母亲的生日的学生数;90﹣10﹣30=50,
这所学校所有知道母亲的生日的学生:990×=550,
故选:C.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,以及利用样本估计总体.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
2.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.1000只 B.10000只 C.5000只 D.50000只
【分析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有100只,根据比例即可解答.
【解答】解:100÷=10000只.
故选:B.
【点评】本题考查了用样本估计总体的知识,体现了统计思想,统计的思想就是用样本的信息来估计总体的信息.
3.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
【分析】随机抽取的50名学生的成绩是一个样本,可以用这个样本的优秀率去估计总体的优秀率,从而求得该校七年级学生在这次数学测试中达到优秀的人数.
【解答】解:随机抽取了50名学生的成绩进行统计,共有15名学生成绩达到优秀,
∴样本优秀率为:15÷50=30%,
又∵某校七年级共320名学生参加数学测试,
∴该校七年级学生在这次数学测试中达到优秀的人数为:320×30%=96人.
故选:D.
【点评】本题考查了用样本估计总体,这是统计的基本思想.一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
4.为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱动画节目的学生约有( )
A.500名 B.600名 C.700名 D.800名
【分析】根据扇形统计图求出该校喜爱动画节目的学生所占的百分比,再乘以总人数即可.
【解答】解:根据扇形统计图可得:
该校喜爱动画节目的学生占1﹣35%﹣5%﹣10%﹣20%=30%,
则该校喜爱动画节目的学生约有2000×30%=600(名);
故选:B.
【点评】此题考查了用样本估计总体,关键是根据扇形统计图求出该校喜爱动画节目的学生所占的百分比,用样本估计整体让整体×样本的百分比即可.
5.2006年1月1日起,某市全面推行农村合作医疗,农民每年每人只拿出10元就可以享受合作医疗.某人住院费报销了805元,则花费了( )
住院费(元) 报销率(%)
不超过3000元部分 15
3000﹣4000部分 25
4000﹣5000部分 30
5000﹣10000部分 35
10000﹣20000部分 40
超过20000部分 45
A.3220 B.4183.33 C.4350 D.4500
【分析】首先计算表中在各个住院的费用段报销的最大数额,从而确定这个人住院费的范围,然后即可根据报销的方法,列出方程解决.
【解答】解:报销金额为:3000×15%=450元、1000×25%=250元、1000×30%=300元,450元+250元=700元<805元,450+250+300=1000元>805元,所以花费总钱数小于5000元且大于4000元.
设可报销率为30%的住院费花去了x元
∴3000×15%+1000×25%+30%x=805,解得x=350元
∴住院费报销了805元,则花费的总钱数为:3000+1000+350=4350元.
故选:C.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
6.下表选自北京师范大学出版社出版的《数学》课本(九年级下册).
全国能源消费总量及其构成统计表
年份 能源消费总量/万吨标准煤 能源消费构成/%
原煤 原油 天然气 水电
1993 115993 74.7 18.2 1.9 5.2
1994 122737 75.0 17.4 1.9 5.7
1995 131176 74.6 17.5 1.8 6.1
1996 138948 74.7 18.0 1.8 5.5
1997 138173 71.5 20.4 1.7 6.2
1998 132214 69.6 21.5 2.2 6.7
全国能源生产总量及其构成统计表
年份 能源生产总量/万吨标准煤 能源生产结构/%
原煤 原油 天然气 水电
1993 111059 74.0 18.7 2.0 5.3
1994 118729 74.6 17.6 1.9 5.9
1995 129034 75.3 16.6 1.9 6.2
1996 132616 75.2 17.0 2.0 5.8
1997 132410 74.1 17.3 2.1 6.5
1998 124250 71.9 18.5 2.5 7.1
下列说法:
1、从1993到1998年,能源消费总量和能源生产总量的变化趋势是一致的;
2、从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例越来越少;
3、1998年和1997年相比,水电消费总量的增长率是0.5%;
4、从1993到1998年,能源生产中,天然气生产总量越来越多.
其中正确的是( )
A.①③ B.①④ C.③④ D.①②
【分析】根据两个表中的信息,对每种说法进行判断即可.
【解答】解:由表中数据可得:从1993到1998年,能源消费总量和能源生产总量的变化趋势都是先增后减,所以变化趋势是一致的,故1正确;
从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例呈先增后减趋势,故2错误;
1998年和1997年相比,水电消费总量由6.2%增长为6.7%,所以其增长了0.5%,故3正确;
从1993到1998年,能源生产中,天然气生产总量呈先减后增趋势,故4错误.
故选:A.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元) 300 280 260 220
入住率 65% 75% 85% 95%
A.300元 B.280元 C.260元 D.220元
【分析】先分别算出三种房价时的收入,再比较选择最高的.
【解答】解:假设房价为300元时,客房的收入=100×65%×300=19500元;
假设房价为280元时,客房的收入=100×75%×280=21000元;
假设房价为260元时,客房的收入=100×85%×260=22100元;
假设房价为220元时,客房的收入=100×95%×220=20900元;
∴客房的定价为260元时,客房的收入最高.
故选:C.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
8.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
项目人数级别 三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
A.3项 B.4项 C.5项 D.6项
【分析】获奖人次共计18+3+6+2+12+3=44人次,减去只获两项奖的13人计13×2=26人次,则剩下44﹣13×2=18人次.
28﹣13=15人,这15人中有只获一次奖的,有获三次以上奖的.
【解答】解:根据题意,要使“该班获得奖励最多的一位同学”获奖最多,则让剩下的15人中的一人获奖最多,其余15﹣1=14人获奖最少,只获一项奖励,则获奖最多的人获奖项目为18﹣14=4项.
故选:B.
【点评】本题考查从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
9.要反映青岛市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.频数分布图 D.折线统计图
【分析】根据折线统计图的特点:①能清楚地反映事物的变化情况,②显示数据变化趋势进行判断,即可得出答案.
【解答】解:要反映青岛市一天内气温的变化情况宜采用折线统计图;
故选:D.
【点评】本题主要考查了统计图的选用,解题时注意:根据具体问题选择合适的统计图,可以使数据变得清晰直观.
10.下列说法不正确的是( )
A.为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图
B.为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图
C.为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图
D.以上三种统计图都可以直接找到所需数目
【分析】根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:A、为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图,说法正确;
B、为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图,说法正确;
C、为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图,说法正确;
D、以上三种统计图都可以直接找到所需数目,说法错误,扇形图找不到所需数目;
故选:D.
【点评】此题主要考查了统计图的特点,关键是掌握扇形统计图、折线统计图、条形统计图各自的特点.
11.为了记录一个病人的体温变化情况,应选择的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
【分析】根据条形统计图、扇形统计图以及折线统计图的特征进行选择即可.
【解答】解:为了记录一个病人的体温变化情况,应选择的统计图是折线统计图,
故选:C.
【点评】本题考查了统计量的选择,掌握条形统计图、扇形统计图以及折线统计图的特征是解题的关键.
12.空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )
A.折线图 B.条形图 C.直方图 D.扇形图
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目;
频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
【解答】解:由分析可知,要求直观反映空气的组成情况,即各部分在总体中所占的百分比,结合统计图各自的特点,应选择扇形统计图.
故选:D.
【点评】本题考查扇形统计图、折线统计图、条形统计图,理解各自的特点是解题的关键.
二.填空题(共8小题)
13.为了估计不透明的袋子里装有多少小球,先从袋中摸出10个小球都做上标记,然后放回袋中去,充分摇匀后再摸出10个小球,发现其中有2个小球有标记,那么可估计袋中原来大约有 50 个小球.
【分析】根据概率公式,设袋中大约有x个球,由题意得=,再求解即可.
【解答】解:设袋中大约有x个小球,由题意得:
=,
解得:x=50.
故答案为:50.
【点评】本题考查了用样本估计总体,关键是设出未知数,根据概率公式,列出方程,运用了用样本估计总体的思想.
14.某校在一次期末考试中,随机抽取八年级30名学生的数学成绩进行分析,其中3名学生的数学成绩达108分以上,据此估计该校八年级630名学生中期末考试数学成绩达108分以上的学生约有 63 名.
【分析】先求出随机抽取的30名学生中成绩达到108分以上的所占的百分比,再乘以630,即可得出答案.
【解答】解:∵随机抽取30名学生的数学成绩进行分析,有3名学生的成绩达108分以上,
∴八年级630名学生中期末考试数学成绩达108分以上的学生约有630×=63(名);
故答案为:63.
【点评】此题考查了用样本估计总体,用到的知识点是总体平均数约等于样本平均数.
15.某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有 800 人.
【分析】根据样本的数据,可得样本中选修A课程的学生所占的比例,利用样本估计总体,用总人数乘以选修A课程的学生所占的比例,可得答案.
【解答】解:选修A课程的学生所占的比例:=,
选修A课程的学生有:2000×=800(人),
故答案为:800.
【点评】本题考查了用样本估计总体,先求出样本所占的比例,估计总体中所占的比例.也考查了条形统计图,条形统计图能清楚地表示出每个项目的数据.
16.免交农业税,大大提高了农民的生产积极性,镇政府引导农民对生产的某种土特产进行加工后,分为甲、乙、丙三种不同包装推向市场进行销售,其相关信息如下表:
质量(克/袋) 销售价(元/袋) 包装成本费用(元/袋)
甲 400 4.8 0.5
乙 300 3.6 0.4
丙 200 2.5 0.3
春节期间,这三种不同包装的土特产都销售了12000千克,那么本次销售中,这三种包装的土特产获得利润最大的是 丙 .
【分析】由题意可得,首先计算胡每种包装中,土特产的售价,即可作出判断.
【解答】解:甲的售价为12000÷0.4×(4.8+0.5)=159000元,
乙的售价为12000÷0.3×(3.6+0.4)=160000元,
丙的售价为12000÷0.2×(2.5+0.3)=168000元,
又每千克的成本价一样,
则这三种包装的土特产获得利润最大的是丙.
【点评】此题考查学生读图获取信息的能力和有理数运算的应用.
17.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a﹣b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号) ②③④ .
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
【分析】根据题意,甲乙的成绩一样好;故两人命中的比例相等,易得a+b=18,且a:b=2:1,解可得a=12,b=6;可得a﹣b=6,a:18=2:3;故②③④正确.
【解答】解:答案②③④
【点评】本题考查学生对统计表的理解与运用.
18.某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.1 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有 6 人,视力为1.0的有 8 人,视力小于1.0的有 26 人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有 24 人,视力正常的人数占全班人数的 48 %;
(3)该班学生视力情况 一般 (选填“好”“一般”“差”).
【分析】由表中信息可得:视力为1.5的有6人,视力为1.0的有8人,视力小于1.0的有1+1+3+4+3+4+4+6=26人;
视力在1.0以上(包括1.0)的为正常,则视力正常的有8+10+6=24人,视力正常的人数占全班人数的×100%=48%,因为正常人数不到50%,所以该班学生视力情况一般.
【解答】解:答案(1)6 8 26(2)24 48(3)一般
【点评】本题考查从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
19.据统计,近几年全世界森林面积以每年约1700万公顷的速度消失,为了预测未来20年世界森林面积的变化趋势,可选用 折线 统计图表示收集到的数据.
【分析】根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:为了预测未来20年世界森林面积的变化趋势,可选用折线统计图表示收集到的数据.
故答案为:折线.
【点评】此题主要考查了统计图的选择,关键是掌握扇形统计图、折线统计图、条形统计图各自的特点.
20.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 折线 统计图来描述数据.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
三.解答题(共8小题)
21.某学校抽查了某班级某月10天的用电量,数据如下表(单位:度);
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是 13度 ,中位数是 13度 ,极差是 7度 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
【分析】(1)分别利用众数、中位数及极差的定义求解即可;
(2)用加权平均数的计算方法计算平均用电量即可;
(3)用班级数乘以日平均用电量乘以天数即可求得总用电量.
【解答】解:(1)13度出现了3次,最多,故众数为13度;
第5天和第天的用电量均是13度,故中位数为13度;
极差为:15﹣8=7度;
(2)平均用电量为:(8+9+10×2+13×3+14+15×2)÷10=12度;
(3)总用电量为20×12×30=7200度.
【点评】本题考查了统计的有关概念及用样本估计总体的知识,题目相对比较简单,属于基础题.
22.“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区10户居民的日用电量,数据如下:
用户序号 1 2 3 4 5 6 7 8 9 10
日用电量(度) 4.4 4.0 5.0 5.6 3.4 4.8 3.4 5.2 4.0 4.2
(1)求这组数据的极差和平均数;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
【分析】(1)根据极差和平均数的概念求解即可,极差是指一组数据中最大数据与最小数据的差.
(2)先求出这10户居民这一天平均每户节约的度数,再用样本估计总体的方法求出该小区200户居民这一天共节约了多少度电.
【解答】解:(1)这组数据中,日用电量最多的是5.6,最少的是3.4,
∴极差=5.6﹣3.4=2.2,
平均数=(4.4+4.0+5.0+5.6+3.4+4.8+3.4+5.2+4.0+4.2)÷10=4.4;
(2)这10户居民这一天平均每户节约:7.8﹣4.4=3.4(度)
∴总数为:3.4×200=680(度).
【点评】本题考查了用样本估计总体、算术平均数和极差的知识,解题时牢记知识要点是解题的关键.
23.某公司为了了解公司每天的用电情况,抽查了某月10天全公司的用电数量,数据如下表(单位:度):
度数 90 100 102 110 116 120
天数 1 1 2 3 1 2
(1)求出上表中数据的众数和平均数;
(2)根据获得的数据,估计该公司本月的用电数量(按30天计算);若每度电的定价为0.5元,试估算本月的电费支出约多少元?
【分析】(1)利用众数和平均数的定义解答;
(2)算出每天的用电量×30×0.5=本月的电费.
【解答】解:(1)这组数据的众数为110;
平均数为.
(2)估计该公司本月的用电数量为108×30=3240(度);
本月电费支出约为3240×0.5=1620(元)
【点评】本题考查的考点:众数、平均数以及用样本估计总体的方法.
24.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1号 2号 3号 4号 5号 总分
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
【分析】(1)根据优秀率=优秀人数除以总人数计算;
(2)根据中位数的定义求解;
(3)根据平均数和方差的概念计算.
【解答】解:
(1)甲班的优秀率=2÷5=0.4=40%;乙班的优秀率=3÷5=0.6=60%;
(2)甲班5名学生比赛成绩的中位数是97(个);
乙班5名学生比赛成绩的中位数是100(个);
(3)甲班的平均数=(89+100+96+118+97)÷5=100(个),
甲班的方差S甲2=[(89﹣100)2+(100﹣100)2+(96﹣100)2+(118﹣100)2+(97﹣100)2]÷5=94
乙班的平均数=(100+96+110+90+104)÷5=100(个),
乙班的方差S乙2=[(100﹣100)2+(96﹣100)2+(110﹣100)2+(90﹣100)2+(104﹣100)2]÷5=46.4;
∴S甲2>S乙2
(4)乙班定为冠军.因为乙班5名学生的比赛成绩的优秀率比甲班高,中位数比甲班大,方差比甲班小,综合评定乙班踢毽子水平较好.
【点评】本题考查了中位数、平均数和方差等概念以及运用.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.
一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
25.某中学开展以“八荣八耻”为主题的社会主义荣辱观教育活动,举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 15
认真观察阅读统计表后,回答下列问题:
(1)请补充完成这个统计表;
(2)本次参加比赛的总人数是 300 人,本次比赛项目的“众数”是 作文 ;
(3)手抄报作品与漫画作品的获奖人数分别是6人和3人,你认为“手抄报作品比漫画作品的获奖率高”这种说法是否正确,请说明你的理由.
【分析】(1)(2)根据演讲中参赛人数是36人,比例是12%,就可以求出总人数;再根据书法所占的比例可以求出人数,已知人数就可以求出比例,相应的表中的空就可以求出.众数就是出现次数最多的数,因而就可以求出众数;
(3)求出获奖率就可以比较说法是否正确.
【解答】解:(1)书法的人数为:75,作文所占的比例为30%;小品的参赛人数为24;
(2)总人数为36÷12%=300人,众数是作文.
(3)手抄报作品的获奖率是,漫画作品的获奖率是
故这种说法不正确.漫画作品的获奖率高.
【点评】本题主要考查了从统计图中获取信息的能力.也考查了对频率和众数概念的理解.
26.我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
4 5 7 6 3 7 9 4 5 7
7 3 7 5 6 8 7 5 6 8
6 7 4 10 5 6 7 3 9 4
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
【分析】(1)根据测试成绩列频率分布表;
(2)利用平均数、众数的定义进行计算.
(3)用样本估计总体.
【解答】解:(1)统计表如下:
成绩 3 4 5 6 7 8 9 10
人数 3 4 5 5 8 2 2 1
(2)平均数(3×3+4×4+5×5+6×5+7×8+8×2+9×2+10×1)
=×180=6
众数为7;
(3)估计300名学生中成绩合格的约有300×=180(人).
答:估计有180人合格.
【点评】本题考查了平均数和众数的概念以及用样本估计总体思想运用.注意:在整理数据时要细心.
27.2007年12月31日,国务院办公厅关于限制生产销售使用塑料购物袋的通知要求:从2008年6月1日起,在全国范围内禁止生产,销售,使用厚度小于0.025毫米的塑料购物袋(以下简称超薄塑料购物袋).
2007年底,某校初四年级一班的同学到学校附近的农贸市场调查了这个市场里100家商户中的10家.这10家商户平均每天送出的超薄塑料购物袋数量分别为(单位:把):
4 5 3 8 5 7 5 6 3 4
(1)请分别写出这组数据的众数,中位数;
(2)如果要选择一种统计图来表示这10家商户送出的超薄塑料购物袋的情况,在条形统计图,折线统计图,扇形统计图中你会选择哪一个;
(3)已知一把超薄塑料购物袋有50个.通过对样本的计算,估计该农贸市场一年要送出多少个超薄塑料购物袋?(一年按350个营业日计算)结果用科学记数法表示.
【分析】(1)根据中位数、众数的定义可得答案;
(2)分析题目中所给统计表的数据,明确其意义,然后根据题意选择出合适的统计图即可;
(3)用样本估计总体.
【解答】解:(1)在数据4、5、3、8、5、7、5、6、3、4中,5出现次数最多,故众数为5;
将数据从大到小排列可得:8、7、6、5、5、5、4、4、3,可知:最中间的两个数为5,故中位数为5.
(2)条形统计图:
(3)用样本估计总体可得:
农贸市场一年要送出大约:350×50×10×(4+5+3+8+5+7+5+6+3+4)=8.75×106(个).
【点评】本题考查统计的知识,涉及知识点有:众数,中位数的概念与求法;常用统计图的作法;用样本估计总体.
28.2005年5月20日《成都商报》报道:四川第二家民营航空公司﹣﹣西部航空有限责任公司即将诞生,公司基地落户绵阳.组建该公司的投资公司及注册的投资资本如下表:
投资公司(简称) 海特投资 惠建立 三星通用航空 翔龙进出口 国瑞投资 银燕创新
投资成本(万元) 3000 3000 1500 1300 700 500
请回答下列问题:
(1)西部航空有限责任公司申请注册的资本为多少元?(用科学记数法表示)
(2)将上述统计表用一种合适的统计图来表示.
【分析】(1)用科学记数法表示即可.
(2)首先分析题目中所给统计表的数据,明确其意义;然后根据题意选择并作出合适统计图即可.
【解答】解:(1)西部航空有限责任公司申请注册资本为:3000+3000+1500+1300+700+500=10000(万元)=108(元).
(2)用扇形统计图表达为(如下左图);用直方图表达为(如下右图).
【点评】本题考查扇形统计图、折线统计图、条形统计图各自的定义、意义,作法.
扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
一.选择题(共12小题)
1.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A.440 B.495 C.550 D.660
2.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.1000只 B.10000只 C.5000只 D.50000只
3.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
4.为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱动画节目的学生约有( )
A.500名 B.600名 C.700名 D.800名
5.2006年1月1日起,某市全面推行农村合作医疗,农民每年每人只拿出10元就可以享受合作医疗.某人住院费报销了805元,则花费了( )
住院费(元) 报销率(%)
不超过3000元部分 15
3000﹣4000部分 25
4000﹣5000部分 30
5000﹣10000部分 35
10000﹣20000部分 40
超过20000部分 45
A.3220 B.4183.33 C.4350 D.4500
6.下表选自北京师范大学出版社出版的《数学》课本(九年级下册).
全国能源消费总量及其构成统计表
年份 能源消费总量/万吨标准煤 能源消费构成/%
原煤 原油 天然气 水电
1993 115993 74.7 18.2 1.9 5.2
1994 122737 75.0 17.4 1.9 5.7
1995 131176 74.6 17.5 1.8 6.1
1996 138948 74.7 18.0 1.8 5.5
1997 138173 71.5 20.4 1.7 6.2
1998 132214 69.6 21.5 2.2 6.7
全国能源生产总量及其构成统计表
年份 能源生产总量/万吨标准煤 能源生产结构/%
原煤 原油 天然气 水电
1993 111059 74.0 18.7 2.0 5.3
1994 118729 74.6 17.6 1.9 5.9
1995 129034 75.3 16.6 1.9 6.2
1996 132616 75.2 17.0 2.0 5.8
1997 132410 74.1 17.3 2.1 6.5
1998 124250 71.9 18.5 2.5 7.1
下列说法:
1、从1993到1998年,能源消费总量和能源生产总量的变化趋势是一致的;
2、从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例越来越少;
3、1998年和1997年相比,水电消费总量的增长率是0.5%;
4、从1993到1998年,能源生产中,天然气生产总量越来越多.
其中正确的是( )
A.①③ B.①④ C.③④ D.①②
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元) 300 280 260 220
入住率 65% 75% 85% 95%
A.300元 B.280元 C.260元 D.220元
8.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
项目人数级别 三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
A.3项 B.4项 C.5项 D.6项
9.要反映青岛市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.频数分布图 D.折线统计图
10.下列说法不正确的是( )
A.为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图
B.为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图
C.为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图
D.以上三种统计图都可以直接找到所需数目
11.为了记录一个病人的体温变化情况,应选择的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
12.空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )
A.折线图 B.条形图 C.直方图 D.扇形图
二.填空题(共8小题)
13.为了估计不透明的袋子里装有多少小球,先从袋中摸出10个小球都做上标记,然后放回袋中去,充分摇匀后再摸出10个小球,发现其中有2个小球有标记,那么可估计袋中原来大约有 个小球.
14.某校在一次期末考试中,随机抽取八年级30名学生的数学成绩进行分析,其中3名学生的数学成绩达108分以上,据此估计该校八年级630名学生中期末考试数学成绩达108分以上的学生约有 名.
15.某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有 人.
16.免交农业税,大大提高了农民的生产积极性,镇政府引导农民对生产的某种土特产进行加工后,分为甲、乙、丙三种不同包装推向市场进行销售,其相关信息如下表:
质量(克/袋) 销售价(元/袋) 包装成本费用(元/袋)
甲 400 4.8 0.5
乙 300 3.6 0.4
丙 200 2.5 0.3
春节期间,这三种不同包装的土特产都销售了12000千克,那么本次销售中,这三种包装的土特产获得利润最大的是 .
17.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a﹣b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号) .
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
18.某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.1 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有 人,视力为1.0的有 人,视力小于1.0的有 人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有 人,视力正常的人数占全班人数的 %;
(3)该班学生视力情况 (选填“好”“一般”“差”).
19.据统计,近几年全世界森林面积以每年约1700万公顷的速度消失,为了预测未来20年世界森林面积的变化趋势,可选用 统计图表示收集到的数据.
20.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 统计图来描述数据.
三.解答题(共8小题)
21.某学校抽查了某班级某月10天的用电量,数据如下表(单位:度);
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是 ,中位数是 ,极差是 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
22.“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区10户居民的日用电量,数据如下:
用户序号 1 2 3 4 5 6 7 8 9 10
日用电量(度) 4.4 4.0 5.0 5.6 3.4 4.8 3.4 5.2 4.0 4.2
(1)求这组数据的极差和平均数;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
23.某公司为了了解公司每天的用电情况,抽查了某月10天全公司的用电数量,数据如下表(单位:度):
度数 90 100 102 110 116 120
天数 1 1 2 3 1 2
(1)求出上表中数据的众数和平均数;
(2)根据获得的数据,估计该公司本月的用电数量(按30天计算);若每度电的定价为0.5元,试估算本月的电费支出约多少元?
24.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1号 2号 3号 4号 5号 总分
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
25.某中学开展以“八荣八耻”为主题的社会主义荣辱观教育活动,举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 15
认真观察阅读统计表后,回答下列问题:
(1)请补充完成这个统计表;
(2)本次参加比赛的总人数是 人,本次比赛项目的“众数”是 ;
(3)手抄报作品与漫画作品的获奖人数分别是6人和3人,你认为“手抄报作品比漫画作品的获奖率高”这种说法是否正确,请说明你的理由.
26.我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
4 5 7 6 3 7 9 4 5 7
7 3 7 5 6 8 7 5 6 8
6 7 4 10 5 6 7 3 9 4
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
27.2007年12月31日,国务院办公厅关于限制生产销售使用塑料购物袋的通知要求:从2008年6月1日起,在全国范围内禁止生产,销售,使用厚度小于0.025毫米的塑料购物袋(以下简称超薄塑料购物袋).
2007年底,某校初四年级一班的同学到学校附近的农贸市场调查了这个市场里100家商户中的10家.这10家商户平均每天送出的超薄塑料购物袋数量分别为(单位:把):
4 5 3 8 5 7 5 6 3 4
(1)请分别写出这组数据的众数,中位数;
(2)如果要选择一种统计图来表示这10家商户送出的超薄塑料购物袋的情况,在条形统计图,折线统计图,扇形统计图中你会选择哪一个;
(3)已知一把超薄塑料购物袋有50个.通过对样本的计算,估计该农贸市场一年要送出多少个超薄塑料购物袋?(一年按350个营业日计算)结果用科学记数法表示.
28.2005年5月20日《成都商报》报道:四川第二家民营航空公司﹣﹣西部航空有限责任公司即将诞生,公司基地落户绵阳.组建该公司的投资公司及注册的投资资本如下表:
投资公司(简称) 海特投资 惠建立 三星通用航空 翔龙进出口 国瑞投资 银燕创新
投资成本(万元) 3000 3000 1500 1300 700 500
请回答下列问题:
(1)西部航空有限责任公司申请注册的资本为多少元?(用科学记数法表示)
(2)将上述统计表用一种合适的统计图来表示.
2020年湘教新版九年级上册数学《第5章 用样本推断总体》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.母亲节快到了,某校团委随机抽取本校部分同学,进行母亲生日日期了解情况调查,分“知道、不知道、记不清”三种情况.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.请你根据图中提供的信息,若全校共有990名学生,估计这所学校所有知道母亲的生日的学生有( )名.
A.440 B.495 C.550 D.660
【分析】根据记不清在扇形统计图中所占120°,在条形图中为30,得出总人数,根据(1)中所求总人数,即可求出调查的学生中“知道”的学生数,再利用样本估计总体的方法计算出答案即可.
【解答】解:调查的总人数:30÷=90,
知道母亲的生日的学生数;90﹣10﹣30=50,
这所学校所有知道母亲的生日的学生:990×=550,
故选:C.
【点评】本题考查的是条形统计图和扇形统计图的综合运用,以及利用样本估计总体.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
2.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉100只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉500只,其中有标记的雀鸟有5只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.1000只 B.10000只 C.5000只 D.50000只
【分析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到.而在总体中,有标记的共有100只,根据比例即可解答.
【解答】解:100÷=10000只.
故选:B.
【点评】本题考查了用样本估计总体的知识,体现了统计思想,统计的思想就是用样本的信息来估计总体的信息.
3.某校七年级共320名学生参加数学测试,随机抽取50名学生的成绩进行统计,其中15名学生成绩达到优秀,估计该校七年级学生在这次数学测试中达到优秀的人数大约有( )
A.50人 B.64人 C.90人 D.96人
【分析】随机抽取的50名学生的成绩是一个样本,可以用这个样本的优秀率去估计总体的优秀率,从而求得该校七年级学生在这次数学测试中达到优秀的人数.
【解答】解:随机抽取了50名学生的成绩进行统计,共有15名学生成绩达到优秀,
∴样本优秀率为:15÷50=30%,
又∵某校七年级共320名学生参加数学测试,
∴该校七年级学生在这次数学测试中达到优秀的人数为:320×30%=96人.
故选:D.
【点评】本题考查了用样本估计总体,这是统计的基本思想.一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.
4.为调查某校2000名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况.随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱动画节目的学生约有( )
A.500名 B.600名 C.700名 D.800名
【分析】根据扇形统计图求出该校喜爱动画节目的学生所占的百分比,再乘以总人数即可.
【解答】解:根据扇形统计图可得:
该校喜爱动画节目的学生占1﹣35%﹣5%﹣10%﹣20%=30%,
则该校喜爱动画节目的学生约有2000×30%=600(名);
故选:B.
【点评】此题考查了用样本估计总体,关键是根据扇形统计图求出该校喜爱动画节目的学生所占的百分比,用样本估计整体让整体×样本的百分比即可.
5.2006年1月1日起,某市全面推行农村合作医疗,农民每年每人只拿出10元就可以享受合作医疗.某人住院费报销了805元,则花费了( )
住院费(元) 报销率(%)
不超过3000元部分 15
3000﹣4000部分 25
4000﹣5000部分 30
5000﹣10000部分 35
10000﹣20000部分 40
超过20000部分 45
A.3220 B.4183.33 C.4350 D.4500
【分析】首先计算表中在各个住院的费用段报销的最大数额,从而确定这个人住院费的范围,然后即可根据报销的方法,列出方程解决.
【解答】解:报销金额为:3000×15%=450元、1000×25%=250元、1000×30%=300元,450元+250元=700元<805元,450+250+300=1000元>805元,所以花费总钱数小于5000元且大于4000元.
设可报销率为30%的住院费花去了x元
∴3000×15%+1000×25%+30%x=805,解得x=350元
∴住院费报销了805元,则花费的总钱数为:3000+1000+350=4350元.
故选:C.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
6.下表选自北京师范大学出版社出版的《数学》课本(九年级下册).
全国能源消费总量及其构成统计表
年份 能源消费总量/万吨标准煤 能源消费构成/%
原煤 原油 天然气 水电
1993 115993 74.7 18.2 1.9 5.2
1994 122737 75.0 17.4 1.9 5.7
1995 131176 74.6 17.5 1.8 6.1
1996 138948 74.7 18.0 1.8 5.5
1997 138173 71.5 20.4 1.7 6.2
1998 132214 69.6 21.5 2.2 6.7
全国能源生产总量及其构成统计表
年份 能源生产总量/万吨标准煤 能源生产结构/%
原煤 原油 天然气 水电
1993 111059 74.0 18.7 2.0 5.3
1994 118729 74.6 17.6 1.9 5.9
1995 129034 75.3 16.6 1.9 6.2
1996 132616 75.2 17.0 2.0 5.8
1997 132410 74.1 17.3 2.1 6.5
1998 124250 71.9 18.5 2.5 7.1
下列说法:
1、从1993到1998年,能源消费总量和能源生产总量的变化趋势是一致的;
2、从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例越来越少;
3、1998年和1997年相比,水电消费总量的增长率是0.5%;
4、从1993到1998年,能源生产中,天然气生产总量越来越多.
其中正确的是( )
A.①③ B.①④ C.③④ D.①②
【分析】根据两个表中的信息,对每种说法进行判断即可.
【解答】解:由表中数据可得:从1993到1998年,能源消费总量和能源生产总量的变化趋势都是先增后减,所以变化趋势是一致的,故1正确;
从1993到1998年,能源消费总量和能源生产总量中,原煤所占比例呈先增后减趋势,故2错误;
1998年和1997年相比,水电消费总量由6.2%增长为6.7%,所以其增长了0.5%,故3正确;
从1993到1998年,能源生产中,天然气生产总量呈先减后增趋势,故4错误.
故选:A.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
7.宾馆有100间相同的客房,经过一段时间的经营,发现客房定价与客房的入住率之间有下表所示的关系,按照这个关系,要使客房的收入最高,每间客房的定价应为( )
每间房价(元) 300 280 260 220
入住率 65% 75% 85% 95%
A.300元 B.280元 C.260元 D.220元
【分析】先分别算出三种房价时的收入,再比较选择最高的.
【解答】解:假设房价为300元时,客房的收入=100×65%×300=19500元;
假设房价为280元时,客房的收入=100×75%×280=21000元;
假设房价为260元时,客房的收入=100×85%×260=22100元;
假设房价为220元时,客房的收入=100×95%×220=20900元;
∴客房的定价为260元时,客房的收入最高.
故选:C.
【点评】本题考查统计表的制作与从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
8.某班学生在颁奖大会上得知该班获得奖励的情况如下表:已知该班共有28人获得奖励,其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
项目人数级别 三好学生 优秀学生干部 优秀团员
市级 3 2 3
校级 18 6 12
A.3项 B.4项 C.5项 D.6项
【分析】获奖人次共计18+3+6+2+12+3=44人次,减去只获两项奖的13人计13×2=26人次,则剩下44﹣13×2=18人次.
28﹣13=15人,这15人中有只获一次奖的,有获三次以上奖的.
【解答】解:根据题意,要使“该班获得奖励最多的一位同学”获奖最多,则让剩下的15人中的一人获奖最多,其余15﹣1=14人获奖最少,只获一项奖励,则获奖最多的人获奖项目为18﹣14=4项.
故选:B.
【点评】本题考查从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
9.要反映青岛市一天内气温的变化情况宜采用( )
A.条形统计图 B.扇形统计图 C.频数分布图 D.折线统计图
【分析】根据折线统计图的特点:①能清楚地反映事物的变化情况,②显示数据变化趋势进行判断,即可得出答案.
【解答】解:要反映青岛市一天内气温的变化情况宜采用折线统计图;
故选:D.
【点评】本题主要考查了统计图的选用,解题时注意:根据具体问题选择合适的统计图,可以使数据变得清晰直观.
10.下列说法不正确的是( )
A.为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图
B.为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图
C.为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图
D.以上三种统计图都可以直接找到所需数目
【分析】根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:A、为了反映雅安市七县一区人口分布多少情况,通常选择条形统计图,说法正确;
B、为了反映我市连续五年来中国民生产总值增长情况,通常选择折线统计图,说法正确;
C、为了反映本校中学生人数占全市中学学生人数的比例情况,应选择扇形统计图,说法正确;
D、以上三种统计图都可以直接找到所需数目,说法错误,扇形图找不到所需数目;
故选:D.
【点评】此题主要考查了统计图的特点,关键是掌握扇形统计图、折线统计图、条形统计图各自的特点.
11.为了记录一个病人的体温变化情况,应选择的统计图是( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
【分析】根据条形统计图、扇形统计图以及折线统计图的特征进行选择即可.
【解答】解:为了记录一个病人的体温变化情况,应选择的统计图是折线统计图,
故选:C.
【点评】本题考查了统计量的选择,掌握条形统计图、扇形统计图以及折线统计图的特征是解题的关键.
12.空气是混合物,为直观介绍空气各成分的百分比,最适合用的统计图是( )
A.折线图 B.条形图 C.直方图 D.扇形图
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目;
频数分布直方图,清楚显示在各个不同区间内取值,各组频数分布情况,易于显示各组之间频数的差别.
【解答】解:由分析可知,要求直观反映空气的组成情况,即各部分在总体中所占的百分比,结合统计图各自的特点,应选择扇形统计图.
故选:D.
【点评】本题考查扇形统计图、折线统计图、条形统计图,理解各自的特点是解题的关键.
二.填空题(共8小题)
13.为了估计不透明的袋子里装有多少小球,先从袋中摸出10个小球都做上标记,然后放回袋中去,充分摇匀后再摸出10个小球,发现其中有2个小球有标记,那么可估计袋中原来大约有 50 个小球.
【分析】根据概率公式,设袋中大约有x个球,由题意得=,再求解即可.
【解答】解:设袋中大约有x个小球,由题意得:
=,
解得:x=50.
故答案为:50.
【点评】本题考查了用样本估计总体,关键是设出未知数,根据概率公式,列出方程,运用了用样本估计总体的思想.
14.某校在一次期末考试中,随机抽取八年级30名学生的数学成绩进行分析,其中3名学生的数学成绩达108分以上,据此估计该校八年级630名学生中期末考试数学成绩达108分以上的学生约有 63 名.
【分析】先求出随机抽取的30名学生中成绩达到108分以上的所占的百分比,再乘以630,即可得出答案.
【解答】解:∵随机抽取30名学生的数学成绩进行分析,有3名学生的成绩达108分以上,
∴八年级630名学生中期末考试数学成绩达108分以上的学生约有630×=63(名);
故答案为:63.
【点评】此题考查了用样本估计总体,用到的知识点是总体平均数约等于样本平均数.
15.某学校计划开设A,B,C,D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如图所示的条形统计图,已知该校学生人数为2000人,由此估计选修A课程的学生有 800 人.
【分析】根据样本的数据,可得样本中选修A课程的学生所占的比例,利用样本估计总体,用总人数乘以选修A课程的学生所占的比例,可得答案.
【解答】解:选修A课程的学生所占的比例:=,
选修A课程的学生有:2000×=800(人),
故答案为:800.
【点评】本题考查了用样本估计总体,先求出样本所占的比例,估计总体中所占的比例.也考查了条形统计图,条形统计图能清楚地表示出每个项目的数据.
16.免交农业税,大大提高了农民的生产积极性,镇政府引导农民对生产的某种土特产进行加工后,分为甲、乙、丙三种不同包装推向市场进行销售,其相关信息如下表:
质量(克/袋) 销售价(元/袋) 包装成本费用(元/袋)
甲 400 4.8 0.5
乙 300 3.6 0.4
丙 200 2.5 0.3
春节期间,这三种不同包装的土特产都销售了12000千克,那么本次销售中,这三种包装的土特产获得利润最大的是 丙 .
【分析】由题意可得,首先计算胡每种包装中,土特产的售价,即可作出判断.
【解答】解:甲的售价为12000÷0.4×(4.8+0.5)=159000元,
乙的售价为12000÷0.3×(3.6+0.4)=160000元,
丙的售价为12000÷0.2×(2.5+0.3)=168000元,
又每千克的成本价一样,
则这三种包装的土特产获得利润最大的是丙.
【点评】此题考查学生读图获取信息的能力和有理数运算的应用.
17.右表为甲、乙两人比赛投篮球的记录,以命中率(投进球数与投球次数的比值)来比较投球成绩的好坏,得知他们的成绩一样好,下面有四个a,b的关系式:①a﹣b=5;②a+b=18;③a:b=2:1;④a:18=2:3.其中正确的是(只填序号) ②③④ .
学生 投进球数 没投进球数 投球次数
甲 10 5 15
乙 a b 18
【分析】根据题意,甲乙的成绩一样好;故两人命中的比例相等,易得a+b=18,且a:b=2:1,解可得a=12,b=6;可得a﹣b=6,a:18=2:3;故②③④正确.
【解答】解:答案②③④
【点评】本题考查学生对统计表的理解与运用.
18.某班50名学生右眼视力的检查结果如下表:
视力 0.1 0.1 0.3 0.4 0.5 0.6 0.7 0.8 1.0 1.2 1.5
人数 1 1 3 4 3 4 4 6 8 10 6
(1)视力为1.5的有 6 人,视力为1.0的有 8 人,视力小于1.0的有 26 人.
(2)视力在1.0以上(包括1.0)的为正常,则视力正常的有 24 人,视力正常的人数占全班人数的 48 %;
(3)该班学生视力情况 一般 (选填“好”“一般”“差”).
【分析】由表中信息可得:视力为1.5的有6人,视力为1.0的有8人,视力小于1.0的有1+1+3+4+3+4+4+6=26人;
视力在1.0以上(包括1.0)的为正常,则视力正常的有8+10+6=24人,视力正常的人数占全班人数的×100%=48%,因为正常人数不到50%,所以该班学生视力情况一般.
【解答】解:答案(1)6 8 26(2)24 48(3)一般
【点评】本题考查从统计表中获取信息的能力.统计表可以将大量数据的分类结果清晰、一目了然地表达出来.
19.据统计,近几年全世界森林面积以每年约1700万公顷的速度消失,为了预测未来20年世界森林面积的变化趋势,可选用 折线 统计图表示收集到的数据.
【分析】根据统计图的特点进行分析可得:扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:为了预测未来20年世界森林面积的变化趋势,可选用折线统计图表示收集到的数据.
故答案为:折线.
【点评】此题主要考查了统计图的选择,关键是掌握扇形统计图、折线统计图、条形统计图各自的特点.
20.某超市对今年前两个季度每月销售总量进行统计,为了更清楚地看出销售总量的总趋势是上升还是下降,应选用 折线 统计图来描述数据.
【分析】扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
【解答】解:根据题意,得
要求清楚地表示销售总量的总趋势是上升还是下降,结合统计图各自的特点,应选用折线统计图.
【点评】此题考查扇形统计图、折线统计图、条形统计图各自的特点.
三.解答题(共8小题)
21.某学校抽查了某班级某月10天的用电量,数据如下表(单位:度);
度数 8 9 10 13 14 15
天数 1 1 2 3 1 2
(1)这10天用电量的众数是 13度 ,中位数是 13度 ,极差是 7度 ;
(2)求这个班级平均每天的用电量;
(3)已知该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
【分析】(1)分别利用众数、中位数及极差的定义求解即可;
(2)用加权平均数的计算方法计算平均用电量即可;
(3)用班级数乘以日平均用电量乘以天数即可求得总用电量.
【解答】解:(1)13度出现了3次,最多,故众数为13度;
第5天和第天的用电量均是13度,故中位数为13度;
极差为:15﹣8=7度;
(2)平均用电量为:(8+9+10×2+13×3+14+15×2)÷10=12度;
(3)总用电量为20×12×30=7200度.
【点评】本题考查了统计的有关概念及用样本估计总体的知识,题目相对比较简单,属于基础题.
22.“珍惜能源从我做起,节约用电人人有责”.为了解某小区居民节约用电情况,物业公司随机抽取了今年某一天本小区10户居民的日用电量,数据如下:
用户序号 1 2 3 4 5 6 7 8 9 10
日用电量(度) 4.4 4.0 5.0 5.6 3.4 4.8 3.4 5.2 4.0 4.2
(1)求这组数据的极差和平均数;
(2)已知去年同一天这10户居民的平均日用电量为7.8度,请你估计,这天与去年同日相比,该小区200户居民这一天共节约了多少度电?
【分析】(1)根据极差和平均数的概念求解即可,极差是指一组数据中最大数据与最小数据的差.
(2)先求出这10户居民这一天平均每户节约的度数,再用样本估计总体的方法求出该小区200户居民这一天共节约了多少度电.
【解答】解:(1)这组数据中,日用电量最多的是5.6,最少的是3.4,
∴极差=5.6﹣3.4=2.2,
平均数=(4.4+4.0+5.0+5.6+3.4+4.8+3.4+5.2+4.0+4.2)÷10=4.4;
(2)这10户居民这一天平均每户节约:7.8﹣4.4=3.4(度)
∴总数为:3.4×200=680(度).
【点评】本题考查了用样本估计总体、算术平均数和极差的知识,解题时牢记知识要点是解题的关键.
23.某公司为了了解公司每天的用电情况,抽查了某月10天全公司的用电数量,数据如下表(单位:度):
度数 90 100 102 110 116 120
天数 1 1 2 3 1 2
(1)求出上表中数据的众数和平均数;
(2)根据获得的数据,估计该公司本月的用电数量(按30天计算);若每度电的定价为0.5元,试估算本月的电费支出约多少元?
【分析】(1)利用众数和平均数的定义解答;
(2)算出每天的用电量×30×0.5=本月的电费.
【解答】解:(1)这组数据的众数为110;
平均数为.
(2)估计该公司本月的用电数量为108×30=3240(度);
本月电费支出约为3240×0.5=1620(元)
【点评】本题考查的考点:众数、平均数以及用样本估计总体的方法.
24.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)
1号 2号 3号 4号 5号 总分
甲班 89 100 96 118 97 500
乙班 100 95 110 91 104 500
统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,请解答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)计算两班比赛数据的方差;
(4)你认为应该定哪一个班为冠军?为什么?
【分析】(1)根据优秀率=优秀人数除以总人数计算;
(2)根据中位数的定义求解;
(3)根据平均数和方差的概念计算.
【解答】解:
(1)甲班的优秀率=2÷5=0.4=40%;乙班的优秀率=3÷5=0.6=60%;
(2)甲班5名学生比赛成绩的中位数是97(个);
乙班5名学生比赛成绩的中位数是100(个);
(3)甲班的平均数=(89+100+96+118+97)÷5=100(个),
甲班的方差S甲2=[(89﹣100)2+(100﹣100)2+(96﹣100)2+(118﹣100)2+(97﹣100)2]÷5=94
乙班的平均数=(100+96+110+90+104)÷5=100(个),
乙班的方差S乙2=[(100﹣100)2+(96﹣100)2+(110﹣100)2+(90﹣100)2+(104﹣100)2]÷5=46.4;
∴S甲2>S乙2
(4)乙班定为冠军.因为乙班5名学生的比赛成绩的优秀率比甲班高,中位数比甲班大,方差比甲班小,综合评定乙班踢毽子水平较好.
【点评】本题考查了中位数、平均数和方差等概念以及运用.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;平均数的大小与一组数据里的每个数据均有关系,其中任何数据的变动都会相应引起平均数的变动.
一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
25.某中学开展以“八荣八耻”为主题的社会主义荣辱观教育活动,举办了演讲、书法、作文、手抄报、小品、漫画六项比赛(每个同学限报一项),学生参赛情况如下表:
比赛项目 演讲 书法 作文 手抄报 小品 漫画
参赛人数(人) 36 90 60 15
比例(%) 12 25 20 8 15
认真观察阅读统计表后,回答下列问题:
(1)请补充完成这个统计表;
(2)本次参加比赛的总人数是 300 人,本次比赛项目的“众数”是 作文 ;
(3)手抄报作品与漫画作品的获奖人数分别是6人和3人,你认为“手抄报作品比漫画作品的获奖率高”这种说法是否正确,请说明你的理由.
【分析】(1)(2)根据演讲中参赛人数是36人,比例是12%,就可以求出总人数;再根据书法所占的比例可以求出人数,已知人数就可以求出比例,相应的表中的空就可以求出.众数就是出现次数最多的数,因而就可以求出众数;
(3)求出获奖率就可以比较说法是否正确.
【解答】解:(1)书法的人数为:75,作文所占的比例为30%;小品的参赛人数为24;
(2)总人数为36÷12%=300人,众数是作文.
(3)手抄报作品的获奖率是,漫画作品的获奖率是
故这种说法不正确.漫画作品的获奖率高.
【点评】本题主要考查了从统计图中获取信息的能力.也考查了对频率和众数概念的理解.
26.我市某中学为了解九年级300名学生的理化实验操作水平,从中随机抽取30名学生进行测试.下表是这30名学生的测试成绩(分):
4 5 7 6 3 7 9 4 5 7
7 3 7 5 6 8 7 5 6 8
6 7 4 10 5 6 7 3 9 4
(1)请你设计一张统计表,能够清楚反映出各成绩的人数分布情况;
(2)求出这30名学生成绩的平均数、众数;
(3)如果测试成绩6分以上(包括6分)为合格,请估计300名学生中成绩合格的约有多少人?
【分析】(1)根据测试成绩列频率分布表;
(2)利用平均数、众数的定义进行计算.
(3)用样本估计总体.
【解答】解:(1)统计表如下:
成绩 3 4 5 6 7 8 9 10
人数 3 4 5 5 8 2 2 1
(2)平均数(3×3+4×4+5×5+6×5+7×8+8×2+9×2+10×1)
=×180=6
众数为7;
(3)估计300名学生中成绩合格的约有300×=180(人).
答:估计有180人合格.
【点评】本题考查了平均数和众数的概念以及用样本估计总体思想运用.注意:在整理数据时要细心.
27.2007年12月31日,国务院办公厅关于限制生产销售使用塑料购物袋的通知要求:从2008年6月1日起,在全国范围内禁止生产,销售,使用厚度小于0.025毫米的塑料购物袋(以下简称超薄塑料购物袋).
2007年底,某校初四年级一班的同学到学校附近的农贸市场调查了这个市场里100家商户中的10家.这10家商户平均每天送出的超薄塑料购物袋数量分别为(单位:把):
4 5 3 8 5 7 5 6 3 4
(1)请分别写出这组数据的众数,中位数;
(2)如果要选择一种统计图来表示这10家商户送出的超薄塑料购物袋的情况,在条形统计图,折线统计图,扇形统计图中你会选择哪一个;
(3)已知一把超薄塑料购物袋有50个.通过对样本的计算,估计该农贸市场一年要送出多少个超薄塑料购物袋?(一年按350个营业日计算)结果用科学记数法表示.
【分析】(1)根据中位数、众数的定义可得答案;
(2)分析题目中所给统计表的数据,明确其意义,然后根据题意选择出合适的统计图即可;
(3)用样本估计总体.
【解答】解:(1)在数据4、5、3、8、5、7、5、6、3、4中,5出现次数最多,故众数为5;
将数据从大到小排列可得:8、7、6、5、5、5、4、4、3,可知:最中间的两个数为5,故中位数为5.
(2)条形统计图:
(3)用样本估计总体可得:
农贸市场一年要送出大约:350×50×10×(4+5+3+8+5+7+5+6+3+4)=8.75×106(个).
【点评】本题考查统计的知识,涉及知识点有:众数,中位数的概念与求法;常用统计图的作法;用样本估计总体.
28.2005年5月20日《成都商报》报道:四川第二家民营航空公司﹣﹣西部航空有限责任公司即将诞生,公司基地落户绵阳.组建该公司的投资公司及注册的投资资本如下表:
投资公司(简称) 海特投资 惠建立 三星通用航空 翔龙进出口 国瑞投资 银燕创新
投资成本(万元) 3000 3000 1500 1300 700 500
请回答下列问题:
(1)西部航空有限责任公司申请注册的资本为多少元?(用科学记数法表示)
(2)将上述统计表用一种合适的统计图来表示.
【分析】(1)用科学记数法表示即可.
(2)首先分析题目中所给统计表的数据,明确其意义;然后根据题意选择并作出合适统计图即可.
【解答】解:(1)西部航空有限责任公司申请注册资本为:3000+3000+1500+1300+700+500=10000(万元)=108(元).
(2)用扇形统计图表达为(如下左图);用直方图表达为(如下右图).
【点评】本题考查扇形统计图、折线统计图、条形统计图各自的定义、意义,作法.
扇形统计图表示的是部分在总体中所占的百分比,但一般不能直接从图中得到具体的数据;
折线统计图表示的是事物的变化情况;
条形统计图能清楚地表示出每个项目的具体数目.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
