2020年湘教新版九年级下册数学《第3章 投影与视图》单元测试卷(解析版)
文档属性
| 名称 | 2020年湘教新版九年级下册数学《第3章 投影与视图》单元测试卷(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 478.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-21 00:00:00 | ||
图片预览

文档简介
2020年湘教新版九年级下册数学《第3章 投影与视图》单元测试卷
一.选择题(共12小题)
1.下列图形中,是正方体的平面展开图的是( )
A. B.
C. D.
2.如图所示是一个三棱柱纸盒.在下面四个图中,只有一个展开图是这个纸盒的展开图,那么这个展开图是( )
A. B.
C. D.
3.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
4.如图,是一个正方体纸盒的外表面展开图,则这个正方体纸盒是( )
A. B. C. D.
5.在下列各平面图形中,是圆锥的表面展开图的是( )
A. B.
C. D.
6.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的标号是( )
A.①②③④ B.②①③④ C.③②①④ D.④②①③
7.下列几何体中,主视图是三角形的是( )
A. B. C. D.
8.如图所示的几何体的俯视图是( )
A. B. C. D.
9.一个几何体的三视图如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.球 D.三棱柱
10.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
11.下面四个图是同一天四个不同时刻树的影子,其时间由早到晚的顺序为( )
A.1234 B.4312 C.3421 D.4231
12.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
二.填空题(共8小题)
13.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是 .
14.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
15.要把一个正方体的表面展开成平面图形,至少需要剪开 条棱.
16.下列表面展开图的立体图形的名称分别是: 、 、 、 .
17.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
18.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分)
19.如图是一个几何体的三视图,则这个几何体的形状是 .
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
三.解答题(共8小题)
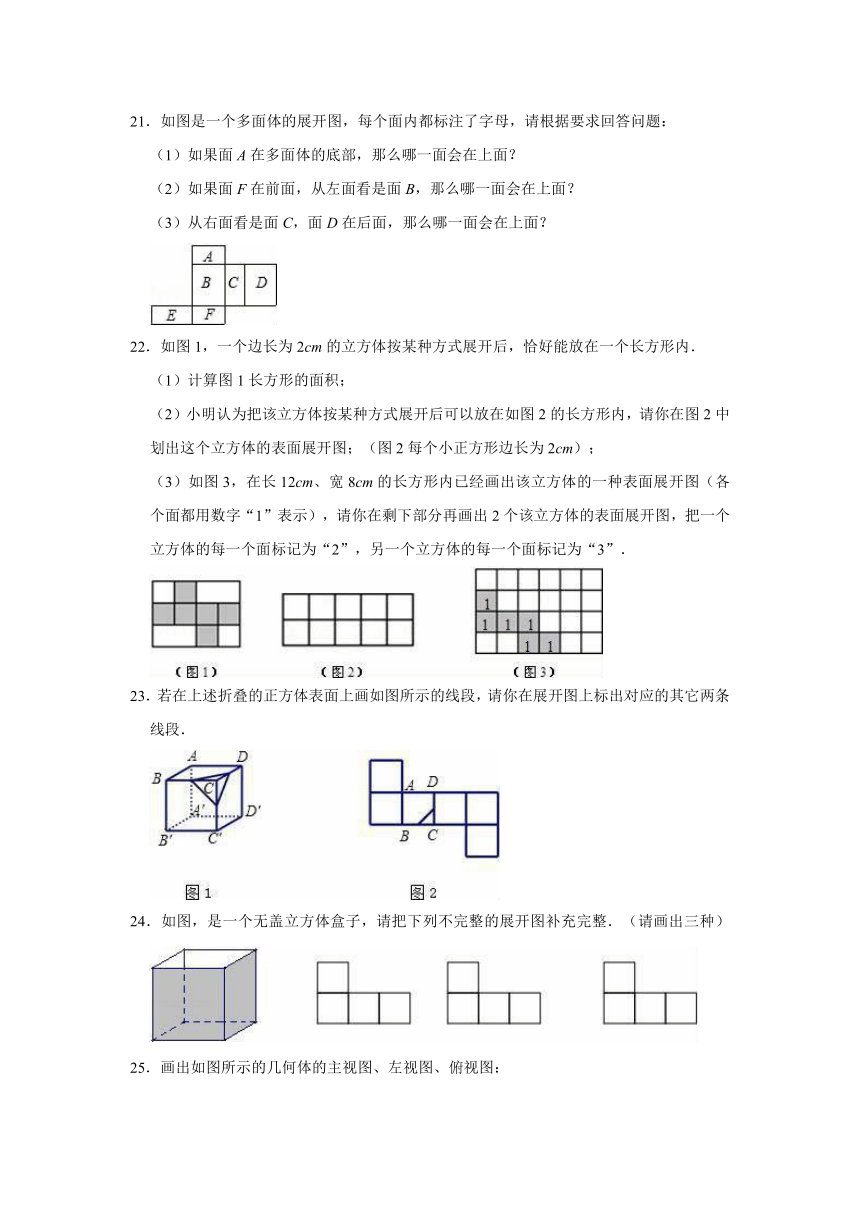
21.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
22.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
23.若在上述折叠的正方体表面上画如图所示的线段,请你在展开图上标出对应的其它两条线段.
24.如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整.(请画出三种)
25.画出如图所示的几何体的主视图、左视图、俯视图:
26.画图题
如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:(要求用直尺或三角板画图)
27.如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请你画出它的主视图和左视图.
28.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
2020年湘教新版九年级下册数学《第3章 投影与视图》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列图形中,是正方体的平面展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:A、折叠后缺少两个底面,故此选项错误;
B、可以是一个正方体的平面展开图,故此选项正确;
C、缺少一个侧面,故此选项错误;
D、折叠后缺少一个底面,上面重合,故此选项错误;
故选:B.
【点评】此题主要考查了正方体展开图,熟练掌握正方体的表面展开图是解题的关键.
2.如图所示是一个三棱柱纸盒.在下面四个图中,只有一个展开图是这个纸盒的展开图,那么这个展开图是( )
A. B.
C. D.
【分析】三棱柱的侧面展开图是三个长方形,底面是三角形,各选项的展开图外形一样,故本题关键是确定描黑部分的分布.
【解答】解:把三棱柱纸盒往上打开为上底面,同时展开侧面,利用空间想象能力,可以确定,D选项符合该展开图.
故选:D.
【点评】此题主要考查了几何体的展开图,注意三棱柱的空间图形,从相对面入手,分析及解答问题.
3.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
【分析】由图可知,这是一个三棱柱的表面展开图,据此可知它的顶点数.
【解答】解:由图可知,这是一个三棱柱的表面展开图,它的顶点数是6个.
故选:B.
【点评】此题考查几何体的展开图,注意培养空间想象能力.
4.如图,是一个正方体纸盒的外表面展开图,则这个正方体纸盒是( )
A. B. C. D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴A符合题意.
故选:A.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
5.在下列各平面图形中,是圆锥的表面展开图的是( )
A. B.
C. D.
【分析】结合圆锥的平面展开图的特征,侧面展开是一个扇形,底面展开是一个圆.
【解答】解:圆锥的展开图是由一个扇形和一个圆形组成的图形.
故选:C.
【点评】考查了几何体的展开图,熟记常见立体图形的展开图的特征,是解决此类问题的关键.注意圆锥的平面展开图是一个扇形和一个圆组成.
6.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的标号是( )
A.①②③④ B.②①③④ C.③②①④ D.④②①③
【分析】根据常见几何体的展开图即可得.
【解答】解:由展开图可知第一个图形是②正方体的展开图,
第2个图形是①圆柱体的展开图,
第3个图形是③三棱柱的展开图,
第4个图形是④四棱锥的展开图,
故选:B.
【点评】本题主要考查几何体的展开图,解题的关键是熟练掌握常见几何体的展开图.
7.下列几何体中,主视图是三角形的是( )
A. B. C. D.
【分析】分别找出四个几何体从正面看所得到的视图即可.
【解答】解:A、此几何体的主视图是矩形,故此选项错误;
B、此几何体的主视图是等腰梯形,故此选项错误;
C、此几何体的主视图是等腰梯形,故此选项错误;
D、此几何体的主视图是等腰三角形,故此选项正确;
故选:D.
【点评】此题主要考查了简单几何体的三视图,关键是注意所有的看到的棱都应表现在三视图中.
8.如图所示的几何体的俯视图是( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意所有看到的棱都应表现在俯视图中.
【解答】解:从上往下看,该几何体的俯视图与选项D所示视图一致.
故选:D.
【点评】本题考查了简单组合体三视图的知识,俯视图是从物体的上面看得到的视图.
9.一个几何体的三视图如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.球 D.三棱柱
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:由于俯视图为圆形可得为球、圆柱、圆锥.主视图和左视图为三角形可得此几何体为圆锥.
故选:A.
【点评】考查学生对圆锥三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
10.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.依此即可解题.
【解答】解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
【点评】本题考查了三种视图及它的画法,看得到的棱画实线,看不到的棱画虚线.
11.下面四个图是同一天四个不同时刻树的影子,其时间由早到晚的顺序为( )
A.1234 B.4312 C.3421 D.4231
【分析】由于太阳早上从东方升起,则早上树的影子向西;傍晚太阳在西边落下,此时树的影子向东,于是可判断四个时刻的时间顺序.
【解答】解:时间由早到晚的顺序为4312.
故选:B.
【点评】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
12.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
【分析】本题考查中心投影的特点.
【解答】解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故选:C.
【点评】本题考查中心投影的特点:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
二.填空题(共8小题)
13.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是 C .
【分析】根据展开图,可的几何体,F、B、C是邻面,F、B、E是邻面,根据F面在前面,B面在左面,可得答案.
【解答】解:由组成几何体面之间的关系,得
F、B、C是邻面,F、B、E是邻面.
由F面在前面,B面在左面,得
C面在上,E面在下,
故答案为:C.
【点评】本题考查了几何体的展开图,利用了几何体展开图组成几何体时面与面之间的关系.
14.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
15.要把一个正方体的表面展开成平面图形,至少需要剪开 7 条棱.
【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着,即可得出答案.
【解答】解:∵正方体有6个表面,12条棱,要展成一个平面图形必须5条棱连接,
∴要剪12﹣5=7条棱,
故答案为:7.
【点评】此题主要考查了正方体的展开图的性质,根据展开图的性质得出一个平面图形必须5条棱连接是解题关键.
16.下列表面展开图的立体图形的名称分别是: 圆柱 、 圆锥 、 四棱锥 、 三棱柱 .
【分析】根据图形结合所学的几何体的形状得出即可.
【解答】解:第一个图是圆柱,第二个图是圆锥,第三个图是四棱柱,第四个图是三棱柱,
故答案为:圆柱,圆锥,四棱锥,三棱柱.
【点评】本题考查了几何体的展开图的应用,主要考查学生的空间想象能力和观察图形的能力.
17.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
【分析】根据左视图是从物体的左面看所得到的图形,判断出此直三棱柱的左视图是以侧棱长为长,以等边三角形的高为宽的矩形,再根据矩形的面积公式列式计算即可得解.
【解答】解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
【点评】本题考查了简单几何体的三视图,等边三角形的性质,本题关键在于判断出左视图的宽是等边三角形的高线.
18.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 ①②③ (多填或错填得0分,少填酌情给分)
【分析】根据几何体的主视图和左视图用正方体实物搭出图形判定,或者根据主视图和左视图想象出每个位置正方体的个数进行计算则可.
【解答】解:综合主视图与左视图,有3行3列.故图形可能是①②③.
故答案为:①②③.
【点评】本题考查了学生的空间想象能力和三种视图的综合能力,难度比较大.
19.如图是一个几何体的三视图,则这个几何体的形状是 圆锥 .
【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据几何体的特点即可得出答案.
【解答】解:根据俯视图为圆的有球,圆锥,圆柱等几何体,主视图和左视图为三角形的只有圆锥,
则这个几何体的形状是圆锥.
故答案为:圆锥.
【点评】此题考查了由三视图判断几何体,关键是对三视图能熟练掌握和灵活运用,体现了对空间想象能力的考查.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 略 .
【分析】由左视图可以知道,左边应该为三个小立方体,且在正前方,添加即可.
【解答】解:
【点评】此题主要考查三视图的画图、学生的观察能力和空间想象能力.
三.解答题(共8小题)
21.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【解答】解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
【点评】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
22.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
【分析】(1)分别求出长方形的长和宽,再利用长方形的面积公式计算即可;
(2)(3)利用正方体及其表面展开图的特点解题.
【解答】解:(1)∵立方体的棱长为2cm,
∴长方形的面积为4×2×3×2=48平方厘米;(3分)
(2)如图所示:
(6分)
(3)如图所示:
【点评】本题考查了几何体的展开图和长方形的面积求法,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
23.若在上述折叠的正方体表面上画如图所示的线段,请你在展开图上标出对应的其它两条线段.
【分析】根据正方体的表面展开图及空间想象能力.在验证立方体的展开图时,要细心观察每一个标志的位置是否一致.
【解答】解:如图所示:
【点评】本题考查了几何体的展开图.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
24.如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整.(请画出三种)
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:如图
【点评】解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
25.画出如图所示的几何体的主视图、左视图、俯视图:
【分析】主视图有3列,每列小正方形数目分别为2,1,1;左视图有3列,每列小正方形数目分别为2,1,1;俯视图,3列,每列小正方形数目分别为3,1,1.
【解答】解:作图如下:
【点评】此题考查的知识点是简单组合体的三视图,关键明确主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
26.画图题
如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:(要求用直尺或三角板画图)
【分析】由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,3,左视图有2列,每列小正方形数目分别为3,3.据此可画出图形.
【解答】解:如图所示:
【点评】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
27.如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请你画出它的主视图和左视图.
【分析】主视图有4列,每列小正方形数目分别为23,2,4;左视图有3列,每列小正方形数目分别为2,3,4.依此画出图形即可求解.
【解答】解:如图所示:
【点评】本题考查了画三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
28.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
【分析】连接AE,过点C作AE的平行线,过点D作BE的平行线,相交于点F,DF即为所求.
【解答】解:
【点评】本题考查平行投影的作图,难度不大,体现了学数学要注重基础知识的新课标理念.会灵活运用性质作图.
一.选择题(共12小题)
1.下列图形中,是正方体的平面展开图的是( )
A. B.
C. D.
2.如图所示是一个三棱柱纸盒.在下面四个图中,只有一个展开图是这个纸盒的展开图,那么这个展开图是( )
A. B.
C. D.
3.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
4.如图,是一个正方体纸盒的外表面展开图,则这个正方体纸盒是( )
A. B. C. D.
5.在下列各平面图形中,是圆锥的表面展开图的是( )
A. B.
C. D.
6.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的标号是( )
A.①②③④ B.②①③④ C.③②①④ D.④②①③
7.下列几何体中,主视图是三角形的是( )
A. B. C. D.
8.如图所示的几何体的俯视图是( )
A. B. C. D.
9.一个几何体的三视图如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.球 D.三棱柱
10.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
11.下面四个图是同一天四个不同时刻树的影子,其时间由早到晚的顺序为( )
A.1234 B.4312 C.3421 D.4231
12.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
二.填空题(共8小题)
13.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是 .
14.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 .
15.要把一个正方体的表面展开成平面图形,至少需要剪开 条棱.
16.下列表面展开图的立体图形的名称分别是: 、 、 、 .
17.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
18.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 (多填或错填得0分,少填酌情给分)
19.如图是一个几何体的三视图,则这个几何体的形状是 .
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 .
三.解答题(共8小题)
21.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
22.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
23.若在上述折叠的正方体表面上画如图所示的线段,请你在展开图上标出对应的其它两条线段.
24.如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整.(请画出三种)
25.画出如图所示的几何体的主视图、左视图、俯视图:
26.画图题
如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:(要求用直尺或三角板画图)
27.如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请你画出它的主视图和左视图.
28.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
2020年湘教新版九年级下册数学《第3章 投影与视图》单元测试卷
参考答案与试题解析
一.选择题(共12小题)
1.下列图形中,是正方体的平面展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:A、折叠后缺少两个底面,故此选项错误;
B、可以是一个正方体的平面展开图,故此选项正确;
C、缺少一个侧面,故此选项错误;
D、折叠后缺少一个底面,上面重合,故此选项错误;
故选:B.
【点评】此题主要考查了正方体展开图,熟练掌握正方体的表面展开图是解题的关键.
2.如图所示是一个三棱柱纸盒.在下面四个图中,只有一个展开图是这个纸盒的展开图,那么这个展开图是( )
A. B.
C. D.
【分析】三棱柱的侧面展开图是三个长方形,底面是三角形,各选项的展开图外形一样,故本题关键是确定描黑部分的分布.
【解答】解:把三棱柱纸盒往上打开为上底面,同时展开侧面,利用空间想象能力,可以确定,D选项符合该展开图.
故选:D.
【点评】此题主要考查了几何体的展开图,注意三棱柱的空间图形,从相对面入手,分析及解答问题.
3.如图是某几何体的表面展开图,则这个几何体的顶点有( )
A.4个 B.6个 C.8个 D.10个
【分析】由图可知,这是一个三棱柱的表面展开图,据此可知它的顶点数.
【解答】解:由图可知,这是一个三棱柱的表面展开图,它的顶点数是6个.
故选:B.
【点评】此题考查几何体的展开图,注意培养空间想象能力.
4.如图,是一个正方体纸盒的外表面展开图,则这个正方体纸盒是( )
A. B. C. D.
【分析】根据几何体的展开图先判断出实心圆点与空心圆点的关系,进而可得出结论.
【解答】解:∵由图可知,实心圆点与空心圆点一定在紧相邻的三个侧面上,
∴A符合题意.
故选:A.
【点评】本题考查的是几何体的展开图,此类问题从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.
5.在下列各平面图形中,是圆锥的表面展开图的是( )
A. B.
C. D.
【分析】结合圆锥的平面展开图的特征,侧面展开是一个扇形,底面展开是一个圆.
【解答】解:圆锥的展开图是由一个扇形和一个圆形组成的图形.
故选:C.
【点评】考查了几何体的展开图,熟记常见立体图形的展开图的特征,是解决此类问题的关键.注意圆锥的平面展开图是一个扇形和一个圆组成.
6.如图,下列四个图形是由已知的四个立体图形展开得到的,则对应的标号是( )
A.①②③④ B.②①③④ C.③②①④ D.④②①③
【分析】根据常见几何体的展开图即可得.
【解答】解:由展开图可知第一个图形是②正方体的展开图,
第2个图形是①圆柱体的展开图,
第3个图形是③三棱柱的展开图,
第4个图形是④四棱锥的展开图,
故选:B.
【点评】本题主要考查几何体的展开图,解题的关键是熟练掌握常见几何体的展开图.
7.下列几何体中,主视图是三角形的是( )
A. B. C. D.
【分析】分别找出四个几何体从正面看所得到的视图即可.
【解答】解:A、此几何体的主视图是矩形,故此选项错误;
B、此几何体的主视图是等腰梯形,故此选项错误;
C、此几何体的主视图是等腰梯形,故此选项错误;
D、此几何体的主视图是等腰三角形,故此选项正确;
故选:D.
【点评】此题主要考查了简单几何体的三视图,关键是注意所有的看到的棱都应表现在三视图中.
8.如图所示的几何体的俯视图是( )
A. B. C. D.
【分析】找到从上面看所得到的图形即可,注意所有看到的棱都应表现在俯视图中.
【解答】解:从上往下看,该几何体的俯视图与选项D所示视图一致.
故选:D.
【点评】本题考查了简单组合体三视图的知识,俯视图是从物体的上面看得到的视图.
9.一个几何体的三视图如图所示,这个几何体是( )
A.圆锥 B.圆柱 C.球 D.三棱柱
【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
【解答】解:由于俯视图为圆形可得为球、圆柱、圆锥.主视图和左视图为三角形可得此几何体为圆锥.
故选:A.
【点评】考查学生对圆锥三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
10.某同学画出了如图所示的几何体的三种视图,其中正确的是( )
A.①② B.①③ C.②③ D.②
【分析】从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.依此即可解题.
【解答】解:根据几何体的摆放位置,主视图和俯视图正确.左视图中间有一条横线,故左视图不正确.
故选:B.
【点评】本题考查了三种视图及它的画法,看得到的棱画实线,看不到的棱画虚线.
11.下面四个图是同一天四个不同时刻树的影子,其时间由早到晚的顺序为( )
A.1234 B.4312 C.3421 D.4231
【分析】由于太阳早上从东方升起,则早上树的影子向西;傍晚太阳在西边落下,此时树的影子向东,于是可判断四个时刻的时间顺序.
【解答】解:时间由早到晚的顺序为4312.
故选:B.
【点评】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
12.两个人的影子在两个相反的方向,这说明( )
A.他们站在阳光下 B.他们站在路灯下
C.他们站在路灯的两侧 D.他们站在月光下
【分析】本题考查中心投影的特点.
【解答】解:根据两个人的影子在两个相反的方向,则一定是中心投影;且两人同在光源两侧.故选:C.
【点评】本题考查中心投影的特点:①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
二.填空题(共8小题)
13.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是 C .
【分析】根据展开图,可的几何体,F、B、C是邻面,F、B、E是邻面,根据F面在前面,B面在左面,可得答案.
【解答】解:由组成几何体面之间的关系,得
F、B、C是邻面,F、B、E是邻面.
由F面在前面,B面在左面,得
C面在上,E面在下,
故答案为:C.
【点评】本题考查了几何体的展开图,利用了几何体展开图组成几何体时面与面之间的关系.
14.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π .
【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解.
【解答】解:①底面周长为6高为16π,
π×()2×16π
=π××16π
=144;
②底面周长为16π高为6,
π×()2×6
=π×64×6
=384π.
答:这个圆柱的体积可以是144或384π.
故答案为:144或384π.
【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用.
15.要把一个正方体的表面展开成平面图形,至少需要剪开 7 条棱.
【分析】根据正方体的棱的条数以及展开后平面之间应有棱连着,即可得出答案.
【解答】解:∵正方体有6个表面,12条棱,要展成一个平面图形必须5条棱连接,
∴要剪12﹣5=7条棱,
故答案为:7.
【点评】此题主要考查了正方体的展开图的性质,根据展开图的性质得出一个平面图形必须5条棱连接是解题关键.
16.下列表面展开图的立体图形的名称分别是: 圆柱 、 圆锥 、 四棱锥 、 三棱柱 .
【分析】根据图形结合所学的几何体的形状得出即可.
【解答】解:第一个图是圆柱,第二个图是圆锥,第三个图是四棱柱,第四个图是三棱柱,
故答案为:圆柱,圆锥,四棱锥,三棱柱.
【点评】本题考查了几何体的展开图的应用,主要考查学生的空间想象能力和观察图形的能力.
17.如图,直三棱柱ABC﹣A1B1C1的侧棱长和底面各边长均为2,其主视图是边长为2的正方形,则此直三棱柱左视图的面积为 .
【分析】根据左视图是从物体的左面看所得到的图形,判断出此直三棱柱的左视图是以侧棱长为长,以等边三角形的高为宽的矩形,再根据矩形的面积公式列式计算即可得解.
【解答】解:此直三棱柱左视图是长为2,宽为AB边上的高的矩形,
∵底面各边长均为2,
∴△ABC是等边三角形,AB边上的高为2×=,
∴此直三棱柱左视图的面积=2×=2.
故答案为:2.
【点评】本题考查了简单几何体的三视图,等边三角形的性质,本题关键在于判断出左视图的宽是等边三角形的高线.
18.如右图,是一个由若干个小正方体搭建而成的几何体的主视图与左视图,那么下列图形中可以作为该几何体的俯视图的序号是 ①②③ (多填或错填得0分,少填酌情给分)
【分析】根据几何体的主视图和左视图用正方体实物搭出图形判定,或者根据主视图和左视图想象出每个位置正方体的个数进行计算则可.
【解答】解:综合主视图与左视图,有3行3列.故图形可能是①②③.
故答案为:①②③.
【点评】本题考查了学生的空间想象能力和三种视图的综合能力,难度比较大.
19.如图是一个几何体的三视图,则这个几何体的形状是 圆锥 .
【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,再根据几何体的特点即可得出答案.
【解答】解:根据俯视图为圆的有球,圆锥,圆柱等几何体,主视图和左视图为三角形的只有圆锥,
则这个几何体的形状是圆锥.
故答案为:圆锥.
【点评】此题考查了由三视图判断几何体,关键是对三视图能熟练掌握和灵活运用,体现了对空间想象能力的考查.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体 略 .
【分析】由左视图可以知道,左边应该为三个小立方体,且在正前方,添加即可.
【解答】解:
【点评】此题主要考查三视图的画图、学生的观察能力和空间想象能力.
三.解答题(共8小题)
21.如图是一个多面体的展开图,每个面内都标注了字母,请根据要求回答问题:
(1)如果面A在多面体的底部,那么哪一面会在上面?
(2)如果面F在前面,从左面看是面B,那么哪一面会在上面?
(3)从右面看是面C,面D在后面,那么哪一面会在上面?
【分析】利用长方体及其表面展开图的特点解题.这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
【解答】解:这是一个长方体的平面展开图,共有六个面,其中面“A”与面“F”相对,面“B”与面“D”相对,面“C”与面“E”相对.
(1)面F会在上面;
(2)面C会在上面;
(3)面A会在上面.
【点评】考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
22.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
【分析】(1)分别求出长方形的长和宽,再利用长方形的面积公式计算即可;
(2)(3)利用正方体及其表面展开图的特点解题.
【解答】解:(1)∵立方体的棱长为2cm,
∴长方形的面积为4×2×3×2=48平方厘米;(3分)
(2)如图所示:
(6分)
(3)如图所示:
【点评】本题考查了几何体的展开图和长方形的面积求法,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
23.若在上述折叠的正方体表面上画如图所示的线段,请你在展开图上标出对应的其它两条线段.
【分析】根据正方体的表面展开图及空间想象能力.在验证立方体的展开图时,要细心观察每一个标志的位置是否一致.
【解答】解:如图所示:
【点评】本题考查了几何体的展开图.易错易混点:学生对相关图的位置想象不准确,从而错选,解决这类问题时,不妨动手实际操作一下,即可解决问题.
24.如图,是一个无盖立方体盒子,请把下列不完整的展开图补充完整.(请画出三种)
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:如图
【点评】解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
25.画出如图所示的几何体的主视图、左视图、俯视图:
【分析】主视图有3列,每列小正方形数目分别为2,1,1;左视图有3列,每列小正方形数目分别为2,1,1;俯视图,3列,每列小正方形数目分别为3,1,1.
【解答】解:作图如下:
【点评】此题考查的知识点是简单组合体的三视图,关键明确主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
26.画图题
如图是一些小正方块所搭几何体的俯视图,小正方块中的数字表示该位置的小方块的个数,请画出这个几何体的主视图和左视图:(要求用直尺或三角板画图)
【分析】由已知条件可知,主视图有3列,每列小正方数形数目分别为3,1,3,左视图有2列,每列小正方形数目分别为3,3.据此可画出图形.
【解答】解:如图所示:
【点评】本题考查几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.
27.如图,这是一个由小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请你画出它的主视图和左视图.
【分析】主视图有4列,每列小正方形数目分别为23,2,4;左视图有3列,每列小正方形数目分别为2,3,4.依此画出图形即可求解.
【解答】解:如图所示:
【点评】本题考查了画三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
28.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
【分析】连接AE,过点C作AE的平行线,过点D作BE的平行线,相交于点F,DF即为所求.
【解答】解:
【点评】本题考查平行投影的作图,难度不大,体现了学数学要注重基础知识的新课标理念.会灵活运用性质作图.
