18.1 平行四边形同步练习题（含答案）

中小学教育资源及组卷应用平台


八年级下册第十八章练习题 (一)
18.1平行四边形
班级　　　 姓名 评价_______　　 　
一、选择题，请把唯一正确选项的字母填在题后的括号里.
1.下面的性质中, 平行四边形不一定具有的是（ ）
A.对角线相等　 B.邻角互补 　 C.对角相等　 　D.对边相等
2. 如图所示，在□ABCD中，CM⊥AD于M，CN⊥AB于N，若∠B=50°，则∠MCN的度数为（ ）
A．40° B．50°
C．60° D．45°
3. 如图，AF∥BG，AB∥CD，CE⊥BG，FG⊥BG，E、G为垂足，则下列说法错误的是（ 　）
A.AB=CD
B.EC=FG
C.线段CE的长表示点C到直线BG的距离
D.直线AF与直线BG的距离就是线段CD的长
4. 在一个平行四边形中若一个角的平分线把一条边分成长是2cm和3cm的两条线段，则该平行四边形的周长为（ ）
A. 14 cm 　　B. 16cm
C. 14 cm或16cm 　　D. 18cm
5．如图所示（1），在△ABC中，D、E分别是AB、AC的中点，将△ADE沿线段DE向下折叠，得到图（2），以下四个结论中，不一定成立的是（ ）
A．点A落在BC边的中点上
B．∠B+∠1+∠C=180°
C．DE=BC
D．DE∥BC
6．以不在同一直线上的三点A、B、C为顶点作平行四边形，一共可以作（ ）
A．1个 B．2个
C．3个 D．4个
7. A、B、C、D在同一平面内，从①AB∥CD，②AB=CD，③BC∥AD，④BC=AD这四个条件中任选两个，能使四边形ABCD是平行四边形的选法有（ ）
A．3种 　B．4种 C．5种 　 D．6种
8．在□ABCD 中，∠A∶∠B∶∠C∶∠D 的值可能是( )
A．2∶5∶2∶5 B．3∶4∶4∶5
C．4∶4∶3∶2 D．2∶3∶5∶6
9．过等腰三角形底边上任意一点作两腰的平行线，与两腰所围成的平行四边形的周长等于该等腰三角形的（ ）
A．两腰长的和 　B．周长的一半
C．周长 　D．一腰长与底边的和
10. 如图所示，已知△ABC的周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边中点构成第三个三角形，依此类推，第2019个三角形的周长为（ ）
A． B．
C． D．
二、填空题，请把答案填在题中横线上.
11. 如图，在平面直角坐标系中，点A、B、C的坐标分别是A（-2，5），B（-3，-1），C（1，-1），在第一象限内找一点D，使四边形ABCD是平行四边形，那么点D的坐标是 .
12. 如图，E，F分别是□ABCD的AD，BC边上的点，若使BE=DF，则需要再增加的一个条件是 　．
13. 已知□ABCD的周长为40cm，对角线AC、BD相交于点O，△BOC的周长比△AOB的周长大2cm，则AB
=_______cm.
14. 如图，E是□ABCD的边 BA延长线上一点，AB=AE，连接CE交AD于点F，若CF平分∠BCD，AB=3，则BC的长为 ．
15. 在?ABCD中，点A1, A2, A3, A4和C1，C2，C3，C4分别是AB和CD的五等分点，点B1, B2和D1, D2分别是BC和DA的三等分点. 已知四边形A4B2C4D2（阴影部分）的面积为1，则?ABCD的面积是 .
三、解答题，应写出推理过程或演算步骤.
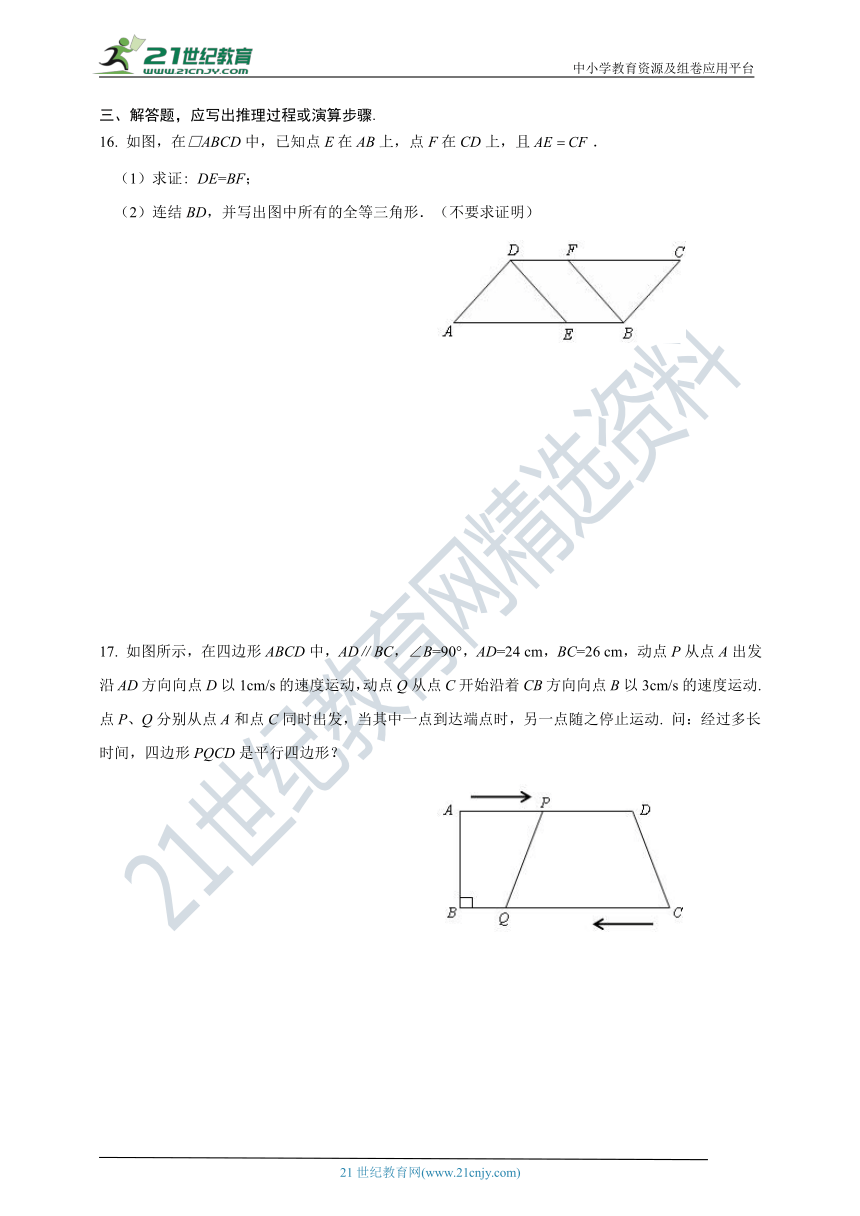
16. 如图，在□ABCD中，已知点E在AB上，点F在CD上，且．
（1）求证: DE=BF；
（2）连结BD，并写出图中所有的全等三角形．（不要求证明）












17. 如图所示，在四边形ABCD中，AD∥BC，∠B=90°，AD=24 cm，BC=26 cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动. 点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动. 问：经过多长时间，四边形PQCD是平行四边形？











18. 如图，四边形ABCD是平行四边形， P是CD上一点，且AP和BP分别平分∠DAB和∠CBA.
(1)求∠APB的度数；
(2)如果AD＝5 cm，AP＝8 cm，求△APB的周长．











19. 如图所示，已知□ABCD中，E为AD的中点，CE交BA的延长线于F,
（1）求证：AB=AF；
（2）若BC=2AB，∠FBC=100°，求∠ABE的度数.














八年级下册第十八章练习题 (一) 参考答案
18.1平行四边形
（总分100分）
一、选择题（每题4分，共40分）
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D C A C B A A C
二、填空题（每题4分，共20分）
11．（2，5） 12. 不唯一，如AE=CF，∠AEB=∠CFD，∠ABE=∠CDF等 13．9
14. 6 15.
三、解答题（共40分）
16.（10分）
（1）∵四边形ABCD是平行四边形，∴AB//CD，AB=CD．
又∵AE=CF，∴BE=DF，又BE//DF，∴四边形BFDE是平行四边形．
∴．（证三角形全等也可）
（2）图中有3对全等三角形：△ADE≌△CBF， △BDE≌△DBF，△ABD≌△CDB．
17．（10分）
解：设经过xs，四边形PQCD为平行四边形.
∵AD∥BC，
∴只要PD =CQ，四边形PQCD就是平行四边形.
据题意得 24 - x=3x，解得x=6．
答：经过6s，四边形PQCD为平行四边形.
18.（9分）
解：(1)∵四边形ABCD是平行四边形，
∴AD∥CB，AB∥CD，AD＝BC，AB＝DC.
∴∠DAB＋∠CBA＝180°.
又∵AP和BP分别平分∠DAB和∠CBA，
∴∠PAB＋∠PBA＝(∠DAB＋∠CBA)＝90°.
∴∠APB＝180°－(∠PAB＋∠PBA)＝90°.
(2)∵AP平分∠DAB，AB∥CD，
∴∠DAP＝∠PAB＝∠DPA.
∴AD＝DP＝5 cm.
同理：PC＝BC＝AD＝5 cm.
∴AB＝DC＝DP＋PC＝10 cm.
在Rt△APB中，AB＝10 cm，AP＝8 cm，
∴BP＝＝6(cm)．
∴△APB的周长为6＋8＋10＝24(cm)．

19.（11分）
（1）易证△AEF≌△DEC（ASA）,
得AF=CD.
又∵四边形ABCD 是平行四边形，
∴AB=CD，∴AF=AB.
（2）法一：由三角形中位线定理得BC=2AE，
又BC=2AB，
∴AE=AB, 又∠EAB=80°, 进而可得∠ABE=50°.
法二：由（1）知：FB=2AB，又BC=2AB，∴FB=BC,
又E是FC的中点，∴BE平分∠FBC, ∴∠ABE=50°.














A1

A

D2

D1

D

A2

A3

A4

B1

B2

C

C2

C1

C3

C4

B



21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）



HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)