京改版九年级数学上册 20.5.4《利用三角函数测高》 同步练习(含答案)
文档属性
| 名称 | 京改版九年级数学上册 20.5.4《利用三角函数测高》 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 462.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-21 19:10:43 | ||
图片预览




文档简介
北京课改版九年级数学上册
20.5.4《利用三角函数测高》
同步练习
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,山顶一铁塔AB在阳光下的投影CD的长为6米,此时太阳光与地面的夹角∠ACD=60°,则铁塔AB的高为( )
A.3米 B.6 米
C.3 米 D.2 米
2.济南大明湖畔的超然楼被称作“江北第一楼”,某校数学社团的同学对超然楼的高度进行了测量.如图,他们在A处仰望塔顶,测得仰角为30°,再往楼的方向前进60 m至B处,测得仰角为60°,若学生的身高忽略不计,≈1.7,结果精确到1 m,则该楼的高度CD为( )
A.47 m B.51 m
C.53 m D.54 m
3. 如图,已知“人字梯”的5个踩档把梯子等分成6份,从上往下的第二个踩档与第三个踩档的正中间处有一条60 cm长的绑绳EF,tan α=,则“人字梯”的顶端离地面的高度AD是( )
A.144 cm B.180 cm
C.240 cm D.360 cm
4.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5 m,AB为1.5 m(即小颖的眼睛与地面的距离),那么树高是( )
A.(+)m B.(+) m
C.(-) m D.(-) m
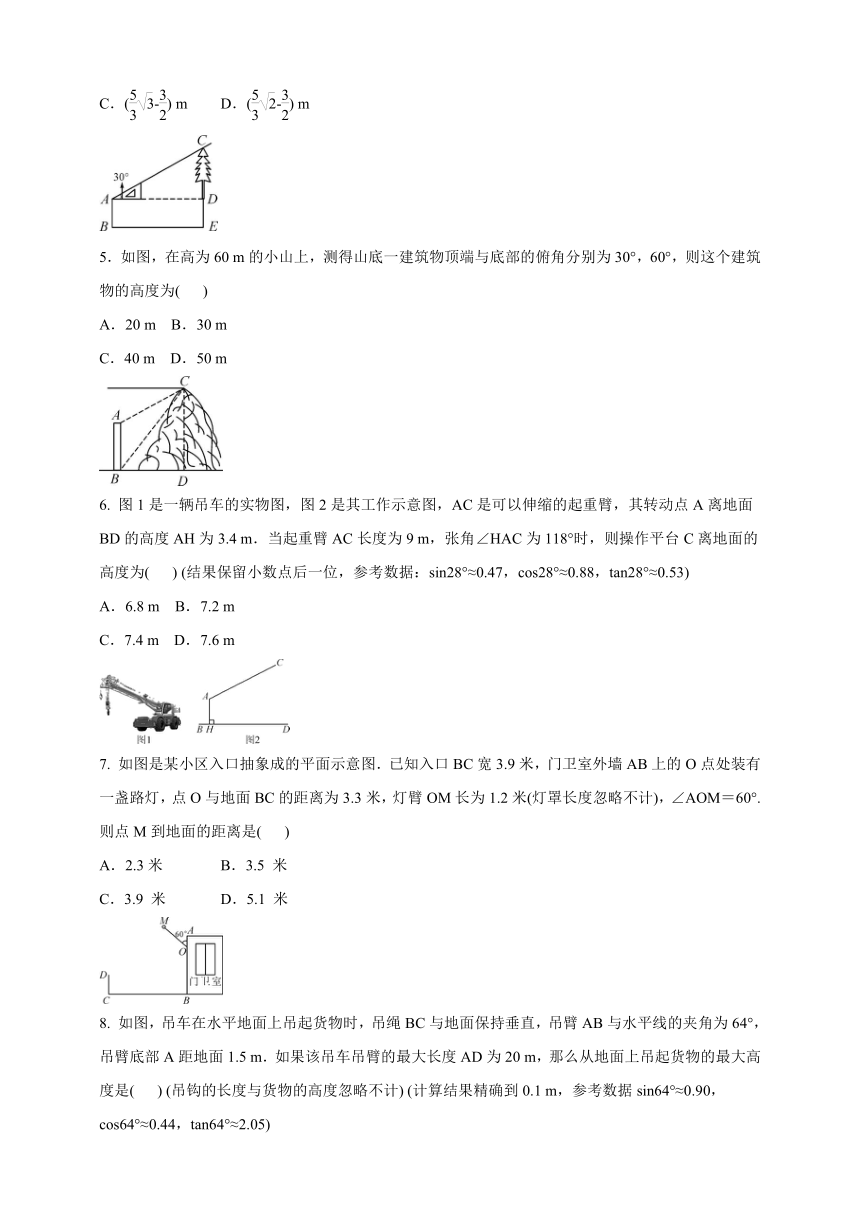
5.如图,在高为60 m的小山上,测得山底一建筑物顶端与底部的俯角分别为30°,60°,则这个建筑物的高度为( )
A.20 m B.30 m
C.40 m D.50 m
6. 图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4 m.当起重臂AC长度为9 m,张角∠HAC为118°时,则操作平台C离地面的高度为( ) (结果保留小数点后一位,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)
A.6.8 m B.7.2 m
C.7.4 m D.7.6 m
7. 如图是某小区入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.则点M到地面的距离是( )
A.2.3米 B.3.5 米
C.3.9 米 D.5.1 米
8. 如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5 m.如果该吊车吊臂的最大长度AD为20 m,那么从地面上吊起货物的最大高度是( ) (吊钩的长度与货物的高度忽略不计) (计算结果精确到0.1 m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
A.20 m B.19.5 m
C.17.9 m D.15.8 m
9.如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,点E离地面的高度EF是( ) (结果精确到1米,参考数据:≈1.4,≈1.7)
A.98米 B.99 米
C.100米 D.101米
10. 滨江公园旁的万寿宝塔始建于明嘉靖年间,周边风景秀丽.现在塔底低于地面约7米,某校学生测得古塔的整体高度约为40米.其测量塔顶相对地面高度的过程如下:先在地面A处测得塔顶的仰角为30°,再向古塔方向行进a米后到达B处,在B处测得塔顶的仰角为45°(如图所示),那么a的值约为( ) (≈1.73,结果精确到0.1)
A.24米 B.24.1米
C.24.3米 D.24.5米
二.填空题(共8小题,3*8=24)
11.每周一学校都要举行庄严的升国旗仪式,让我们体会国旗的神圣,某同学产生了用所学知识测量旗杆高度的想法,在地面距杆脚5 m远的地方,他用测倾器测得杆顶的仰角为α,且tanα=3,则旗杆的高度(不计测倾器的高度)为_________.
12.某校九(1)班课外活动小组为了测得学校旗杆的高度,他们在离旗杆6米的A处,用高为1.5米的仪器测得旗杆顶部B处的仰角为60°,如图,则旗杆的高度为 米(已知≈1.732,结果精确到0.1米).
13.如图,在高为h的山顶上,测得一建筑物顶部与底部的俯角分别为30°和60°,用h表示这个建筑物的高为 _____ .
14.如图,山顶有一座电视塔,在地面上一点A处测得塔顶B处的仰角α=60°,在塔底C处测得A点俯角β=45°,已知塔高60米,则山高CD等于___________.
15. 数学兴趣小组同学进行测量大树CD的实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜坡AB的坡度i=1∶2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)________________.
16. 如图,“人字梯”放在水平的地面上,当梯子的一边与地面所夹的锐角α为60°时,两梯角之间的距离BC的长为3 m.周日亮亮帮助妈妈整理换季衣服,先使α为60°,后又调整α为45°,则梯子顶端离地面的高度AD下降了______________m.(结果保留根号)
17. 如图,为了测量一垂直于水平地面的某建筑物AB的高度,一测量人员在该建筑物附近的C处测得建筑物顶端A处的仰角为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角为30°,则建筑物AB的高度约为_________米.(≈1.41,≈1.73,结果取整数)
18.如图,一枚运载火箭从距雷达站C处5 km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,点O,A,B在同一条直线上,则A,B两点间的距离为_________.(结果精确到0.1 km,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67)
三.解答题(共7小题,46分)
19.(6分) 如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.
20.(6分)如图,两座建筑物AB与CD,其水平距离BD为30米,在从AB的顶点A处用高1.2米的测角仪AE测得CD的顶部C的仰角α=30°,测得其底部D的俯角β=45°,求两座建筑物AB与CD的高(精确到0.1米).
21.(6分)为了测量白塔的高度AB,如图,在D处用高为1.5米的测角仪CD,测得塔顶A的仰角为42°,再向白塔方向前进12米,又测得白塔的顶端A的仰角为61°,求白塔的高度AB(参考数据:sin42°≈0.67,tan42°≈0.90,sin61°≈0.87,tan61°≈1.80,结果保留整数).
22.(6分)如图,两座建筑物的水平距离BC为60 m,从C点测得A点的仰角α为53°,从A点测得D点的俯角β为37°,求两座建筑物的高度.(参考数据:sin37°≈,cos37°≈,tan37°≈,
sin53°≈,cos53°≈,tan53°≈)
23.(6分) 如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走7米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A,B,C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(参考数据:≈1.4,≈1.7)
24.(8分)如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为45°,然后他沿着正对树PQ的方向前进10米到达点B处,此时测得树顶P和树底Q的仰角分别是60°和30°,设PQ垂直于AB,且垂足为C.
(1)求∠BPQ的度数;
(2)求树PQ的高度.(结果精确到0.1 m,≈1.73)
25.(8分)某旅游区有一个景观奇异的望天洞,点D是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处.在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC=10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过点D作地面BE的垂线,垂足为C.求:
(1)∠ADB的度数;
(2)索道AB的长(结果保留根号).
参考答案:
1-5BBBAC 6-10DCBCB
11.15 m
12. 11.9
13. h
14.30(1+)米
15.8.1米
16.
17. 137
18. 1.7km
19. 解:(1)在直角△ABC中,∠BAC=90°,∠BCA=60°,AB=60米,
则AC===20(米),
即坡底C点到大楼距离AC的值是20米
(2)设CD=2x,则DE=x,CE=x,
在Rt△BDF中,∵∠BDF=45°,∴BF=DF,∴60-x=20+x,
∴x=40-60.
∵CD=2x=80-120,∴CD的长为(80-120)米
20. 解:过点E作EF⊥CD于点F.
在矩形EBDF中,EF=BD=30 m,BE=DF.
在Rt△EFC中,CF=EF·tanα=10(m).
在Rt△EFD中,DF=EF·tanβ=30(m).
∴CD=CF+FD=10+30≈47.3(m),
AB=BE-AE=30-1.2=28.8(m).
答:两座建筑物CD与AB的高分别为47.3米和28.8米.
21. 解:设AE=x米.
在Rt△ACE中,CE==(米).
在Rt△AFE中,FE==(米).
由题意,得CF=CE-FE=-=12,
解得x≈21.6.
∴AB=AE+BE≈21.6+1.5≈23(米).
答:这个电视塔的高度AB约为23米.
22. 解:过点D作DE⊥AB于E,则DE=BC=60 m,
在Rt△ABC中,tan53°=,∴=,∴AB=80(m),
在Rt△ADE中,tan37°=,∴=,∴AE=45 m,
∴BE=CD=AB-AE=35(m),
答:两座建筑物的高度分别为80 m和35 m
23. 解:(1)∵四边形ABED是矩形,∴DE=AB=7米.
在Rt△DEH中,∵∠EDH=45°,∴HE=DE=7米,
∴BH=HE+BE=8.5(米)
(2)作HJ⊥CG于J.则△HJG是等腰三角形,四边形BCJH是矩形,
设HJ=GJ=BC=EF=x.
在Rt△GEF中,tan60°=,∴=,
∴x=+.FG=+,
∴CG=CF+FG=1.5++≈17.95(米)
24. 解:延长PQ交直线AB于点C.(1)∠BPQ=90°-60°=30°
(2)设PC=x米,在Rt△APC中,∠PAC=45°,则AC=PC=x米,
∵∠PBC=60°,∴∠BPC=30°,
在Rt△BPC中,BC=PC=x(米),
∵AB=AC-BC=10,∴x-x=10,
解得:x=15+5. 则BC=(5+5)米.
在Rt△BCQ中,QC=BC=(5+5)=(5+)米,
∴PQ=PC-QC=15+5-(5+)=10+≈15.8(米).
答:树PQ的高度约为15.8米
25. 解:(1)∵DC⊥CE,∴∠BCD=90°.
又∵∠DBC=10°,∴∠BDC=80°.
∵∠ADF=85°,
∴∠ADB=360°-80°-90°-85°=105°.
(2)过点D作DG⊥AB于点G.
在Rt△GDB中,∵∠GBD=40°-10°=30°,
∴∠BDG=90°-30°=60°.
又∵BD=100米,
∴GD=BD=50(米),GB=BD·cos30°=50(米).
在Rt△ADG中,∵∠ADG=105°-60°=45°,
∴GA=GD=50米.
∴AB=AG+GB=50+50(米).
答:索道的长为(50+50)米.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
