2019-2020学年高中物理新人教版选修3-3:8.2气体的等容变化和等压变化 课后作业(解析版)
文档属性
| 名称 | 2019-2020学年高中物理新人教版选修3-3:8.2气体的等容变化和等压变化 课后作业(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 149.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-01-21 16:43:48 | ||
图片预览



文档简介
第2节 气体的等容变化和等压变化
1.(查理定律)一个密封的钢管内装有空气,在温度为20 ℃时,压强为1 atm,若温度上升到80 ℃,管内空气的压强约为( )
A.4 atm B. atm
C.1.2 atm D. atm
答案 C
解析 由=得:p2=p1=p1,p2=1.2 atm。
2. (气体的等容变化)(多选)一定质量的气体作等容变化时,其p-t图象如图所示,若保持气体质量不变,而改变容器的容积,再让气体作等容变化,则其等容线与原来相比,下列可能正确的是( )
A.等容线与p轴之间夹角变小
B.等容线与p轴之间夹角变大
C.等容线与t轴交点的位置不变
D.等容线与t轴交点的位置一定改变
答案 ABC
解析 对于一定质量气体等容变化的p-t图线,总是要经过点(-273 ℃,0),因此,C正确,D错误;由于题目没有给定体积变化的情况,所以A、B都有可能。
3.(气体的等压变化)(多选)在下图中,p表示压强,V表示体积,T表示热力学温度,t表示摄氏温度,能正确描述一定质量的气体等压变化规律的是 ( )
答案 AC
解析 一定质量的气体在等压变化中,压强不变,体积V与绝对温度T成正比。其中B图明显看出气体压强减小,观察可知D图中气体压强增大,故只有A、C符合要求。
4.(盖—吕萨克定律)(多选)一定质量的气体在等压变化中体积增大了,若气体原来温度是27 ℃,则温度的变化是( )
A.升高到450 K B.升高了150 ℃
C.升高到40.5 ℃ D.升高到450 ℃
答案 AB
解析 等压变化中,有=,即=,解得x=450 K,故温度会升高到450 K,即升高了150 ℃。
5. (盖—吕萨克定律)如图,某同学用封有气体的玻璃管来测绝对零度,当容器水温是30 ℃时,空气柱长度为30 cm,当水温是90 ℃时,空气柱的长度是36 cm,则该同学测得的绝对零度相当于多少摄氏度( )
A.-273 ℃ B.-270 ℃
C.-268 ℃ D.-271 ℃
答案 B
解析 由等压变化知=所以有=,绝对零度空气柱长为0,故=,得T1=300 K,所以绝对零度应是(30-300) ℃=-270 ℃,B正确。
6.(查理定律)气体温度计结构如图所示。玻璃测温泡A内充有理想气体,通过细玻璃管B和水银压强计相连。开始时A处于冰水混合物中,左管C中水银面在O点处,右管D中水银面高出O点h1=14 cm。后将A放入待测恒温槽中,上下移动D,使C中水银面仍在O点处,测得D中水银面高出O点h2=44 cm。(已知外界大气压为1个标准大气压,1标准大气压相当于76 cmHg)
(1)求恒温槽的温度;
(2)此过程A内气体内能________(填“增大”或“减小”)。
答案 (1)364 K(或91 ℃) (2)增大
解析 (1)设恒温槽的温度为T2,由题意知T1=273 K,
A内气体发生等容变化,根据查理定律得
=①
p1=p0+ph1=p0+p0②
p2=p0+ph2=p0+p0③
联立①②③式,代入数据得T2=364 K(或91 ℃)。
(2)温度升高,A内气体内能增大。
7.(盖—吕萨克定律)一个开着窗户的房间,温度为7 ℃时室内空气质量为m,当温度升高到27 ℃时,室内空气的质量为多少?
答案 m
解析 应用盖—吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为V1,温度升高后体积为V2,已知T1=280 K,T2=300 K,根据盖—吕萨克定律:=得V2=V1=V1=V1。
因温度升高后留在室内的气体体积仍为V1,占总体积的比例为==。所以m2=m。
8. (盖—吕萨克定律)如图所示,在一端开口的钢制圆筒的开口端上面放一活塞,活塞与筒壁间的摩擦及活塞的重力不计,现将其开口端向下,竖直缓慢地放入7 ℃的水中,在筒底与水面相平时,恰好静止在水中,这时筒内气柱长为14 cm,当水温升高到27 ℃时,筒底露出水面的高度为多少?(筒的厚度不计)
答案 1 cm
解析 圆筒的重力等于气体对圆筒的压力,故当水温升高时,筒内的气体发生的是等压变化,设筒底露出水面的高度为h。
当t1=7 ℃即T1=280 K时,V1=14 cm·S
当t2=27 ℃即T2=300 K时,V2=(14 cm+h)·S
由盖—吕萨克定律得=
解得h=1 cm。
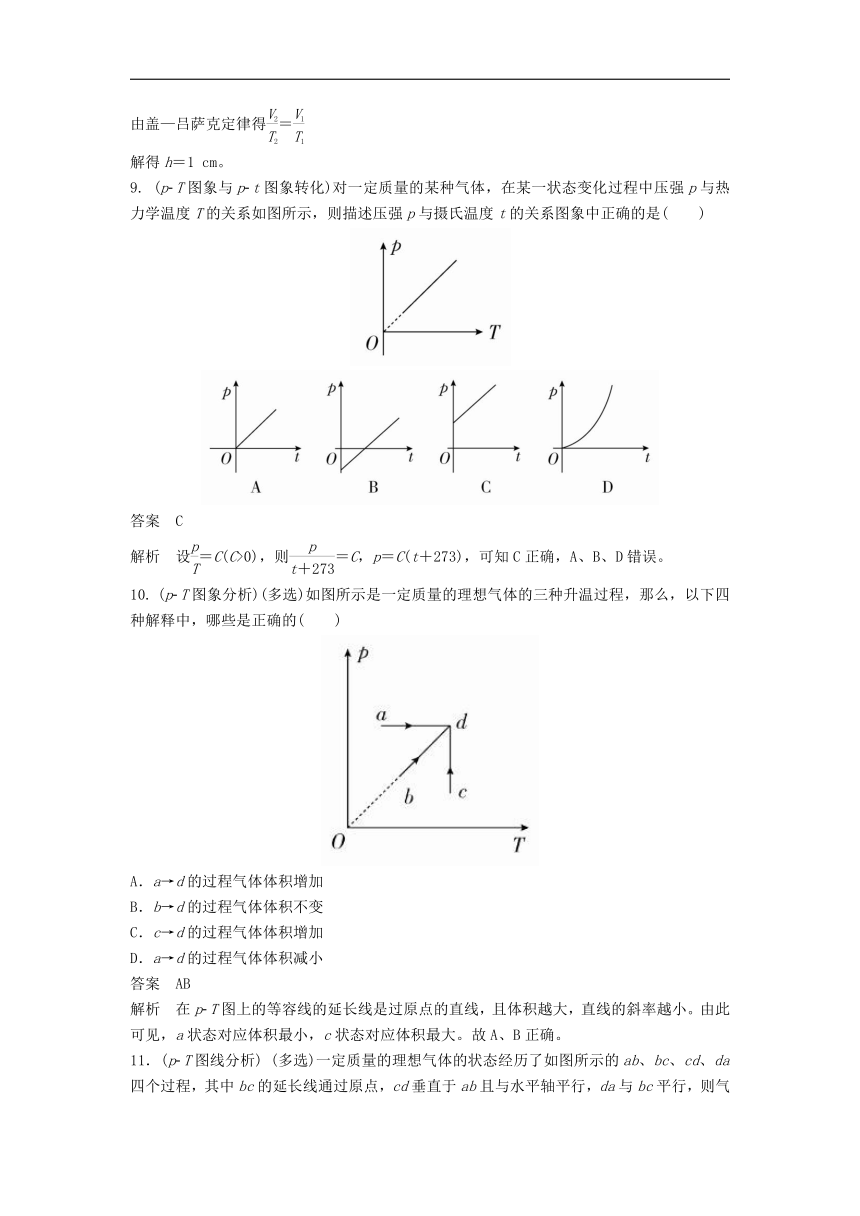
9. (p-T图象与p-t图象转化)对一定质量的某种气体,在某一状态变化过程中压强p与热力学温度T的关系如图所示,则描述压强p与摄氏温度t的关系图象中正确的是( )
答案 C
解析 设=C(C>0),则=C,p=C(t+273),可知C正确,A、B、D错误。
10. (p-T图象分析)(多选)如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的( )
A.a→d的过程气体体积增加
B.b→d的过程气体体积不变
C.c→d的过程气体体积增加
D.a→d的过程气体体积减小
答案 AB
解析 在p-T图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小。由此可见,a状态对应体积最小,c状态对应体积最大。故A、B正确。
11.(p-T图线分析) (多选)一定质量的理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则气体体积在( )
A.ab过程中不断增加 B.bc过程中保持不变
C.cd过程中不断增加 D.da过程中保持不变
答案 AB
解析 因为bc的延长线通过原点,所以bc是等容线,即气体体积在bc过程中保持不变,B正确;ab是等温线,压强减小则体积增大,A正确;cd是等压线,温度降低则体积减小,C错误;如图所示,连接aO交cd于e,则ae是等容线,即Va=Ve,因为Vd<Ve,所以Vd<Va,所以da过程中体积增加,D错误。
12.(气体状态变化的图象转化) (多选)一定质量气体的状态变化过程的p-V图线如图所示,其中A是初状态,B、C是中间状态。A→B为双曲线的一部分,B→C与纵轴平行,C→A与横轴平行。如将上述变化过程改用p-T图线和V-T图线表示,则在下图的各图线中正确的是( )
答案 BD
解析 在p-V图象中,气体由A→B是等温过程,且压强减小,气体体积增大;由B→C是等容过程,且压强增大,气体温度升高;由C→A是等压过程,且体积减小,温度降低。由此可判断在p-T图中A错误、B正确,在V-T图中C错误、D正确。
13.(液柱移动问题)如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着一定质量同温度的空气,空气柱长度H1>H2,水银柱长度h1>h2,今使封闭气柱降低相同的温度(大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向下移动,A管移动较多
B.均向上移动,A管移动较多
C.A管向上移动,B管向下移动
D.无法判断
答案 A
解析 因为在温度降低过程中,被封闭气柱的压强恒等于大气压强与水银柱产生的压强之和,故封闭气柱均做等压变化,并由此推知,封闭气柱下端的水银面高度不变。根据盖—吕萨克定律的分比形式ΔV=·V,因A、B管中的封闭气柱,初温T相同,温度降低量ΔT也相同,且ΔT<0,所以ΔV<0,即A、B管中的气柱体积都减小;又因为H1>H2,故A管中气柱的体积较大,则|ΔV1|>|ΔV2|,即A管中气柱的体积减小得较多,故A、B两管柱上方的水银柱均向下移动,且A管中的水银柱下移得较多。故正确答案为A。
14.(综合)如图所示为0.3 mol的某种气体的压强和温度关系的p-t图线。p0表示1个标准大气压,则在状态B时气体的体积为( )
A.5.6 L B.3.2 L
C.1.2 L D.8.4 L
答案 D
解析 此气体在0 ℃时,压强为标准大气压,所以它的体积应为22.4×0.3 L=6.72 L,根据图线所示,从压强为p0的状态到A状态,气体是等容变化,A状态的体积为6.72 L,温度为(127+273) K=400 K,从A状态到B状态为等压变化,B状态的温度为(227+273) K=500 K,根据盖—吕萨克定律=,VB== L=8.4 L。
15. (综合)一个质量可不计的活塞将一定量的理想气体封闭在上端开口的直立圆筒形汽缸内,活塞上堆放着铁砂,如图所示,最初活塞搁置在汽缸内壁的固定卡环上,气柱的高度为H0,压强等于大气压强p0。现对气体缓慢加热,当气体温度升高了ΔT=60 K时,活塞(及铁砂)开始离开卡环而上升,继续加热直到气柱高度为H1=1.5H0。此后,在维持温度不变的条件下逐渐取走铁砂,直到铁砂全部取走时,气柱高度变为H2=1.8H0,求此时气体的温度。(不计活塞与汽缸之间的摩擦)
答案 540 K
解析 本题包括等容、等压和等温的三个特殊变化过程,当温度升高ΔT=60 K时,活塞开始离开卡环,在此之前的过程属于等容变化过程;继续对气体缓慢加热,气体压强不变,当气柱高度从H0变化到H1=1.5H0时,属于等压变化过程;此后在温度不变的条件下逐渐取走铁砂,气柱高度从H1升高到H2=1.8H0,此过程属于等温变化过程。分别对三个过程列式即可求解。气体温度升高60 K的过程中,活塞没有上升,此过程是等容变化过程,由查理定律得=①
气柱高度从H0变化到H1=1.5H0过程中,压强不变,为等压变化过程,由盖—吕萨克定律得
=②
气柱高度从H1变化到H2的过程中,温度不变,为等温变化过程,由波意耳定律得1.5p1H0=1.8p0H0③
由①②③联立可得T2=540 K。
16.(综合)一定质量的理想气体被活塞封闭在竖直放置的圆柱形汽缸内,汽缸壁导热良好,活塞可沿汽缸壁无摩擦地滑动。开始时气体压强为p,活塞下表面相对于汽缸底部的高度为h,外界的温度为T0。现取质量为m的沙子缓慢地倒在活塞的上表面,沙子倒完时,活塞下降了。若此后外界的温度变为T,求重新达到平衡后气体的体积。已知外界大气的压强始终保持不变,重力加速度大小为g。
答案
解析 设汽缸的横截面积为S,沙子倒在活塞上后,对气体产生的压强为Δp,由玻意耳定律得
phS=(p+Δp)S①
解得Δp=p②
外界的温度变为T后,设活塞距底面的高度为h′。根据盖—吕萨克定律,得
=③
解得h′=h④
据题意可得Δp=⑤
气体最后的体积为V=Sh′⑥
联立②④⑤⑥式得V=。
1.(查理定律)一个密封的钢管内装有空气,在温度为20 ℃时,压强为1 atm,若温度上升到80 ℃,管内空气的压强约为( )
A.4 atm B. atm
C.1.2 atm D. atm
答案 C
解析 由=得:p2=p1=p1,p2=1.2 atm。
2. (气体的等容变化)(多选)一定质量的气体作等容变化时,其p-t图象如图所示,若保持气体质量不变,而改变容器的容积,再让气体作等容变化,则其等容线与原来相比,下列可能正确的是( )
A.等容线与p轴之间夹角变小
B.等容线与p轴之间夹角变大
C.等容线与t轴交点的位置不变
D.等容线与t轴交点的位置一定改变
答案 ABC
解析 对于一定质量气体等容变化的p-t图线,总是要经过点(-273 ℃,0),因此,C正确,D错误;由于题目没有给定体积变化的情况,所以A、B都有可能。
3.(气体的等压变化)(多选)在下图中,p表示压强,V表示体积,T表示热力学温度,t表示摄氏温度,能正确描述一定质量的气体等压变化规律的是 ( )
答案 AC
解析 一定质量的气体在等压变化中,压强不变,体积V与绝对温度T成正比。其中B图明显看出气体压强减小,观察可知D图中气体压强增大,故只有A、C符合要求。
4.(盖—吕萨克定律)(多选)一定质量的气体在等压变化中体积增大了,若气体原来温度是27 ℃,则温度的变化是( )
A.升高到450 K B.升高了150 ℃
C.升高到40.5 ℃ D.升高到450 ℃
答案 AB
解析 等压变化中,有=,即=,解得x=450 K,故温度会升高到450 K,即升高了150 ℃。
5. (盖—吕萨克定律)如图,某同学用封有气体的玻璃管来测绝对零度,当容器水温是30 ℃时,空气柱长度为30 cm,当水温是90 ℃时,空气柱的长度是36 cm,则该同学测得的绝对零度相当于多少摄氏度( )
A.-273 ℃ B.-270 ℃
C.-268 ℃ D.-271 ℃
答案 B
解析 由等压变化知=所以有=,绝对零度空气柱长为0,故=,得T1=300 K,所以绝对零度应是(30-300) ℃=-270 ℃,B正确。
6.(查理定律)气体温度计结构如图所示。玻璃测温泡A内充有理想气体,通过细玻璃管B和水银压强计相连。开始时A处于冰水混合物中,左管C中水银面在O点处,右管D中水银面高出O点h1=14 cm。后将A放入待测恒温槽中,上下移动D,使C中水银面仍在O点处,测得D中水银面高出O点h2=44 cm。(已知外界大气压为1个标准大气压,1标准大气压相当于76 cmHg)
(1)求恒温槽的温度;
(2)此过程A内气体内能________(填“增大”或“减小”)。
答案 (1)364 K(或91 ℃) (2)增大
解析 (1)设恒温槽的温度为T2,由题意知T1=273 K,
A内气体发生等容变化,根据查理定律得
=①
p1=p0+ph1=p0+p0②
p2=p0+ph2=p0+p0③
联立①②③式,代入数据得T2=364 K(或91 ℃)。
(2)温度升高,A内气体内能增大。
7.(盖—吕萨克定律)一个开着窗户的房间,温度为7 ℃时室内空气质量为m,当温度升高到27 ℃时,室内空气的质量为多少?
答案 m
解析 应用盖—吕萨克定律,以跑到室外的气体与室内的气体整体为研究对象,设原来体积为V1,温度升高后体积为V2,已知T1=280 K,T2=300 K,根据盖—吕萨克定律:=得V2=V1=V1=V1。
因温度升高后留在室内的气体体积仍为V1,占总体积的比例为==。所以m2=m。
8. (盖—吕萨克定律)如图所示,在一端开口的钢制圆筒的开口端上面放一活塞,活塞与筒壁间的摩擦及活塞的重力不计,现将其开口端向下,竖直缓慢地放入7 ℃的水中,在筒底与水面相平时,恰好静止在水中,这时筒内气柱长为14 cm,当水温升高到27 ℃时,筒底露出水面的高度为多少?(筒的厚度不计)
答案 1 cm
解析 圆筒的重力等于气体对圆筒的压力,故当水温升高时,筒内的气体发生的是等压变化,设筒底露出水面的高度为h。
当t1=7 ℃即T1=280 K时,V1=14 cm·S
当t2=27 ℃即T2=300 K时,V2=(14 cm+h)·S
由盖—吕萨克定律得=
解得h=1 cm。
9. (p-T图象与p-t图象转化)对一定质量的某种气体,在某一状态变化过程中压强p与热力学温度T的关系如图所示,则描述压强p与摄氏温度t的关系图象中正确的是( )
答案 C
解析 设=C(C>0),则=C,p=C(t+273),可知C正确,A、B、D错误。
10. (p-T图象分析)(多选)如图所示是一定质量的理想气体的三种升温过程,那么,以下四种解释中,哪些是正确的( )
A.a→d的过程气体体积增加
B.b→d的过程气体体积不变
C.c→d的过程气体体积增加
D.a→d的过程气体体积减小
答案 AB
解析 在p-T图上的等容线的延长线是过原点的直线,且体积越大,直线的斜率越小。由此可见,a状态对应体积最小,c状态对应体积最大。故A、B正确。
11.(p-T图线分析) (多选)一定质量的理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中bc的延长线通过原点,cd垂直于ab且与水平轴平行,da与bc平行,则气体体积在( )
A.ab过程中不断增加 B.bc过程中保持不变
C.cd过程中不断增加 D.da过程中保持不变
答案 AB
解析 因为bc的延长线通过原点,所以bc是等容线,即气体体积在bc过程中保持不变,B正确;ab是等温线,压强减小则体积增大,A正确;cd是等压线,温度降低则体积减小,C错误;如图所示,连接aO交cd于e,则ae是等容线,即Va=Ve,因为Vd<Ve,所以Vd<Va,所以da过程中体积增加,D错误。
12.(气体状态变化的图象转化) (多选)一定质量气体的状态变化过程的p-V图线如图所示,其中A是初状态,B、C是中间状态。A→B为双曲线的一部分,B→C与纵轴平行,C→A与横轴平行。如将上述变化过程改用p-T图线和V-T图线表示,则在下图的各图线中正确的是( )
答案 BD
解析 在p-V图象中,气体由A→B是等温过程,且压强减小,气体体积增大;由B→C是等容过程,且压强增大,气体温度升高;由C→A是等压过程,且体积减小,温度降低。由此可判断在p-T图中A错误、B正确,在V-T图中C错误、D正确。
13.(液柱移动问题)如图所示,两根粗细相同、两端开口的直玻璃管A和B,竖直插入同一水银槽中,各用一段水银柱封闭着一定质量同温度的空气,空气柱长度H1>H2,水银柱长度h1>h2,今使封闭气柱降低相同的温度(大气压保持不变),则两管中气柱上方水银柱的移动情况是( )
A.均向下移动,A管移动较多
B.均向上移动,A管移动较多
C.A管向上移动,B管向下移动
D.无法判断
答案 A
解析 因为在温度降低过程中,被封闭气柱的压强恒等于大气压强与水银柱产生的压强之和,故封闭气柱均做等压变化,并由此推知,封闭气柱下端的水银面高度不变。根据盖—吕萨克定律的分比形式ΔV=·V,因A、B管中的封闭气柱,初温T相同,温度降低量ΔT也相同,且ΔT<0,所以ΔV<0,即A、B管中的气柱体积都减小;又因为H1>H2,故A管中气柱的体积较大,则|ΔV1|>|ΔV2|,即A管中气柱的体积减小得较多,故A、B两管柱上方的水银柱均向下移动,且A管中的水银柱下移得较多。故正确答案为A。
14.(综合)如图所示为0.3 mol的某种气体的压强和温度关系的p-t图线。p0表示1个标准大气压,则在状态B时气体的体积为( )
A.5.6 L B.3.2 L
C.1.2 L D.8.4 L
答案 D
解析 此气体在0 ℃时,压强为标准大气压,所以它的体积应为22.4×0.3 L=6.72 L,根据图线所示,从压强为p0的状态到A状态,气体是等容变化,A状态的体积为6.72 L,温度为(127+273) K=400 K,从A状态到B状态为等压变化,B状态的温度为(227+273) K=500 K,根据盖—吕萨克定律=,VB== L=8.4 L。
15. (综合)一个质量可不计的活塞将一定量的理想气体封闭在上端开口的直立圆筒形汽缸内,活塞上堆放着铁砂,如图所示,最初活塞搁置在汽缸内壁的固定卡环上,气柱的高度为H0,压强等于大气压强p0。现对气体缓慢加热,当气体温度升高了ΔT=60 K时,活塞(及铁砂)开始离开卡环而上升,继续加热直到气柱高度为H1=1.5H0。此后,在维持温度不变的条件下逐渐取走铁砂,直到铁砂全部取走时,气柱高度变为H2=1.8H0,求此时气体的温度。(不计活塞与汽缸之间的摩擦)
答案 540 K
解析 本题包括等容、等压和等温的三个特殊变化过程,当温度升高ΔT=60 K时,活塞开始离开卡环,在此之前的过程属于等容变化过程;继续对气体缓慢加热,气体压强不变,当气柱高度从H0变化到H1=1.5H0时,属于等压变化过程;此后在温度不变的条件下逐渐取走铁砂,气柱高度从H1升高到H2=1.8H0,此过程属于等温变化过程。分别对三个过程列式即可求解。气体温度升高60 K的过程中,活塞没有上升,此过程是等容变化过程,由查理定律得=①
气柱高度从H0变化到H1=1.5H0过程中,压强不变,为等压变化过程,由盖—吕萨克定律得
=②
气柱高度从H1变化到H2的过程中,温度不变,为等温变化过程,由波意耳定律得1.5p1H0=1.8p0H0③
由①②③联立可得T2=540 K。
16.(综合)一定质量的理想气体被活塞封闭在竖直放置的圆柱形汽缸内,汽缸壁导热良好,活塞可沿汽缸壁无摩擦地滑动。开始时气体压强为p,活塞下表面相对于汽缸底部的高度为h,外界的温度为T0。现取质量为m的沙子缓慢地倒在活塞的上表面,沙子倒完时,活塞下降了。若此后外界的温度变为T,求重新达到平衡后气体的体积。已知外界大气的压强始终保持不变,重力加速度大小为g。
答案
解析 设汽缸的横截面积为S,沙子倒在活塞上后,对气体产生的压强为Δp,由玻意耳定律得
phS=(p+Δp)S①
解得Δp=p②
外界的温度变为T后,设活塞距底面的高度为h′。根据盖—吕萨克定律,得
=③
解得h′=h④
据题意可得Δp=⑤
气体最后的体积为V=Sh′⑥
联立②④⑤⑥式得V=。
