青岛版数学五四制二年级下册第1单元-信息窗3-5知识点解析及练习(含答案)
文档属性
| 名称 | 青岛版数学五四制二年级下册第1单元-信息窗3-5知识点解析及练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版(五四制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-21 00:00:00 | ||
图片预览





文档简介
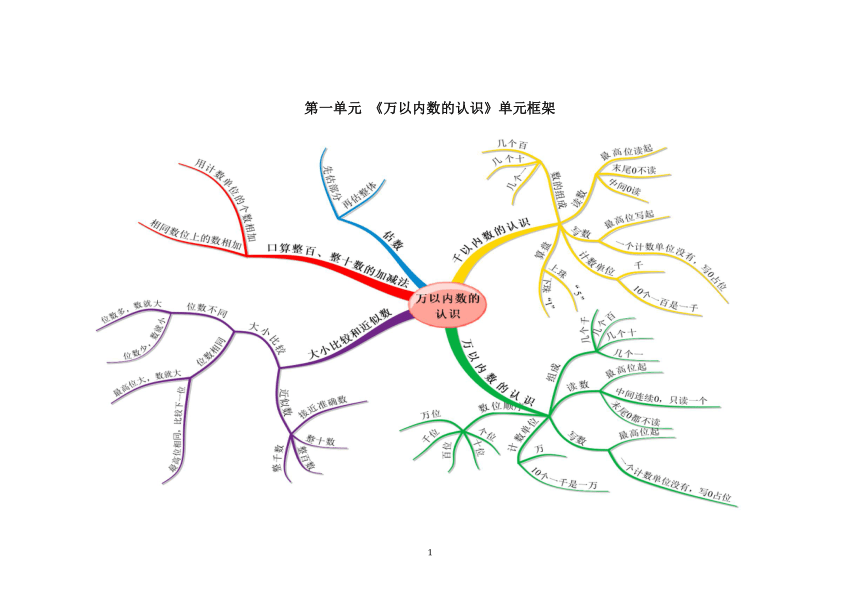
第一单元 《万以内数的认识》单元框架
信息窗3——万以内数的大小比较
一、知识点解读
1.近似数(初步认识)
知识点:与准确数最接近的整千、整百或几千几百、几百几十的数叫近似数,近似数用约等号“≈”连接。一个数的近似数并不唯一,要根据实际需要选择合适的近似数。
教学要求:近似数是与实际非常接近的数。教学时,先放手让学生根据已有经验说一说,然后借助数轴帮助学生直观理解一个数取近似数的方法,从而理解近似数的概念,掌握近似数的表示方法。本窗是对近似数的初步认识,不宜要求过高,近似数只要是接近整十、整百数都可以,后续还要学习用“四舍五入法”取近似数。生活中有时不需要用准确数,用近似数会更方便些。描述近似数时,不要忘记加上“大约”“大概”等标志性词语。
2.位数不同的数比较大小的方法(掌握运用)
知识点:比较位数不同的万以内的数时,根据位数的多少进行比较简单方便,位数多的数一定大于位数少的数。
教学要求:教学该知识点时,要先让学生独立思考,再交流比较大小的方法。学生可能根据位数的多少来比较,还可能根据数的组成来比较,也可能借助一个标准数来比较。对不同的方法教师都应给与及时的鼓励与肯定,使学生体验解决问题策略的多样性。
3.位数相同的数比较大小的方法(掌握运用)
知识点:比较位数相同的万以内数的大小时,先比较最高位上的数,最高位上的数大的那个数就大;如果最高位上的数相同,再依次比较下一位上的数,直到比较出大小。
教学要求:教学该知识点时,要让学生自己比较数的大小,然后交流汇报比较的方法。方法一:位数相同,从高位比起,相同数位上的数大的那个数大;方法二:用取近似数的方法比较大小。鼓励学生用自己喜欢的方法进行比较,重点引导学生理解掌握“从高位依次比较”的方法。
教学时,教师可以引导学生对万以内数大小比较的方法进行综合梳理:两个整数比较大小,位数不同时,位数多的那个数比较大;位数相同时,从高位开始依次进行比较。对于比较方法,重在结合实例进行理解,避免让学生进行机械记忆。
二、知识拓展
运用比较法解决填数问题。
典型例题:□里可以填哪些数?
□46>673 209□<2099
思路分析:□46>673中的两个数都是三位数,因为十位上4﹤7,所以百位上□里的数必须大于6,才能保证第一个数大于第二个数;209□﹤2099中的两个数都是四位数,因为千位、百位和十位上的数都相同,所以□里的数必须小于9,才能保证第一个数小于第二个数。
正确解答:第一个□里可以填7、8、9中的任意一个数;第二个□里可以填0-8中的任意一个数。
方法总结:解决此类问题时,可以利用比较数的大小的方法填数,注意不要遗漏。
三、知识点训练
基础训练
1. 下面各数的近似数是多少?选一选。
(1)上海磁悬浮列车每小时最快能行驶430千米。每小时最快大约行驶( )千米。
① 400 ② 500
(2)胶州湾海底隧道是我国目前最长的海底隧道,它分为陆上与海底两部分,其中海底部分长3950米。海底部分大约长( )米。
① 3000 ②4000
2. 小蜜蜂回家。(连一连)
3.比一比。
4. 在○里填上“>”或“<”。
500○499 2560○2650 3000○3010
828○808 1234○2143 10000○9999
能力提升
1.估一估,填一填。
(1)一辆自行车的价格是398元,大约是( )元。
(2)在一次捐书活动中,二年级共捐图书2015本,大约是( )本。
(3)双山鸭厂养鸭9760只,大约是( )只。
2.把下面各数按要求填入括号里。
999 852 640 365 847 351 1003
(1)在300和400之间的数有( )。
(2)比800大的数有( )。
(3)最接近1000的数是( )。
3. 想一想,连一连。
4. 解决问题。
五岳是中国五大名山的总称,分别是东岳泰山,高1533米;西岳华山,高2155米;南岳衡山,高1300米;北岳恒山,高2016米;中岳嵩山,高1492米。在这五座山中,哪座山最高?哪座山最低?
拓展训练
1. 在里填上合适的数。
49<496 99<1000 117<1177
13>137 853>8□3 4157>417
2. 一个三位数,个位上的数是十位上的数的3倍,十位上的数是百位上的数的3倍,这个三位数是多少?
3. 用8、6、7三个数字摆出不同的三位数,并按照从大到小的顺序排列起来。
训练题参考答案及解析
基础训练
1. (1)① (2)②
2. 接近500的数是:495、504; 接近1000的数是:988、1003、990、1004。
3. 122>97 1850<2020
4. >,<,<,>,<,>
能力提升
1. (1)400 (2)2000(3)10000
2. (1)365、351(2)999、852、847、1003(3)999
3. 新光小学1600人, 民族小学930人, 兴华小学1580人。
4. 因为2155>2016>1533>1492>1300,所以西岳华山最高,南岳衡山最低。
拓展应用
答案不唯一。依次示例:5、9、6、4、3、0。
2. 139
3. 876>867>786>768>687>678
信息窗4——整百、整千数的加减法
一、知识点解读
1.整百数加减整百数、整千数加减整千数的口算方法(掌握运用)
知识点:整百数加减整百数、整千数加减整千数的口算方法:可以先把整百、整千数看成几个百、几个千,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上相应个数的0。
教学要求:教学该知识点时,可以先复习一下100以内整十数加减整十数的口算,增加迁移的效果,然后引导学生通过自主探索、小组合作的方式学习口算方法,然后全班交流。其实,整百数(整千数)加减整百数(整千数)的口算方法就是把整百数(整千数)加减法转化为20以内的加减法。 如果学生想不到,教师可以进行引导,为后面的口算学习作铺垫。
2.几百几十加减几十的口算方法(掌握运用)
知识点:几百几十加减几十的口算方法:可以先把几百几十看成几十几个十,把几十看成几个十,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上1个0。
教学要求:教学时,由于学生已经有了整百数相加减的知识和思维基础,所以可以放手让学生自己解决,然后集体交流。对于学生出现的认知困难,可以借助计数器等直观手段帮助学生理解。
3.几千几百加减几百的口算方法(掌握运用)
知识点:几千几百加减几百的口算方法:可以先把几千几百看成几十几个百,把几百看成几个百,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上2个0。
教学要求:教学时,可以让学生独立解答,然后交流。重点让学生说说口算的方法,只要方法合理即可。对于用计数单位的个数相减的口算方法,教师仍需多加关注。
二、知识拓展
运用综合法和移多补少法解决整百数的加减法问题。
典型例题:小白兔收了400根胡萝卜,小灰兔收了200根胡萝卜,小白兔给小灰兔多少根胡萝卜,它们的胡萝卜就同样多了?
思路分析:
方法一:综合法。先用加法求出胡萝卜的总数,再把总数两等分,其中的一份与小灰兔的胡萝卜数的差就是小白兔给小灰兔的胡萝卜数。
方法二:移多补少法。先求小白兔比小灰兔多多少根胡萝卜,再把多的胡萝卜两等分,其中的一份就是小白兔给小灰兔的胡萝卜数。
正确解答:
方法一:400+200=600(根),600根的一半是300根,300-200=100(根)
方法二:400-200=200(根),200根的一半是100根。所以小白兔给小灰兔100根胡萝卜,它们的胡萝卜就同样多了。
方法总结:解决此类问题时,可以先求出总数,再用总数的一半减去较小的那个数;也可以先求出两个数的差,再把差平均分成两份,其中的一份即为所求。
三、知识点训练
基础训练
1. 填一填。
(1)700+200=( ),想:( )个百加( )个百是( )个百。
(2)1200-300=( ),想:( )个百减( )个百是( )个百。
(3)3000+600=( ),想:( )个百加( )个百是( )个百。
2. 算一算。
400+800= 8000-4000= 900+60= 230+40=
2000-400= 9000-4500= 4300+600= 1100-500=
2800+500= 5300-300= 4000+90= 7000-3000=
3. 在○里填上“>”“<”或“=”。
400+700○2000-800 1400-700○2700-500 6200-800○3200+2000
4600-800○3200+300 1500+600○7200-100 2700-400○1600+700
4. 解决问题。
1路公交车今天运送乘客1300人,2路公交车今天运送乘客900人,3路公交车今天运送乘客700人。
(1)1路公交车比3路公交车多运送乘客多少人?
(2)3辆公交车一共运送乘客多少人?
能力提升
1.把400、500、600、700分别填入括号内,使等式成立。
( )+( )-( )=( )
2. ●-★=1000 ●-★-★=700
●=( ) ★=()
3. 一根绳子长600米,第一次用去了100米,第二次用去了320米,这根绳子短了多少米?
4. 妈妈有1000元,爸爸有400元,妈妈给爸爸多少元后,两人的钱数就同样多了?
拓展训练
甲乙丙三个数的和是1000,甲乙两个数的和是500,乙丙两数的和是700,甲乙丙三数分别是多少?
2. 在下面的○里填上不同的整百数,使每条边上三个数的和都是1000。
3.把一根5米长的竹竿插到井底,取出后又把另一端插到井底。这时,竹竿中间有长60厘米的部分没有湿。你知道井水有多深吗?
训练题参考答案及解析
基础训练
1. (1)900,7,2,9 (2)900,12,3,9(3)3600,30,6,36
2. 1200 4000 960 270
1600 4500 4900 600
3300 5000 4090 4000
3. <,<,>,>,<,=
4.(1)1300-700=600(人),1路公交车比3路公交车多运送乘客600人。
(2)1300+900+700=2900(人),3辆公交车一共运送乘客2900人。
能力提升
1. 答案不唯一。示例:400+700-600=500
2. ●=1300 ★=300
3. 100+320=420(米),这根绳子短了420米。
4. 1000-400=600(元),600元的一半是300元,因此妈妈给爸爸300元后,两人的钱数就同样多了。
拓展应用
1. 乙数:500+700=1200,1200-1000=200
甲数:500-200=300
丙数:700-200=500
答案不唯一。示例:
3. 220厘米。
分析:可以借助画图和学具操作帮助理解。竹竿的长度被分成了3部分,分别是顺着插入井底被浸湿的部分,倒着插入井底被浸湿的部分、中间没有被浸湿的部分。其中两端浸湿部分是相等的,中间没有浸湿的部分是60厘米。列式:5米=500厘米,500-60=440(厘米),440÷2=220(厘米)
信息窗5——估计
一、知识点解读
估计万以内的数(掌握运用)
知识点:估计在生活中应用广泛,包括对长度、高度、质量、时间等的估计。估计时要有根据、讲方法,尽量让估出的数接近准确数。估计的方法有多种,可以凭借经验估计,也可以先数出一部分或圈出一部分,再估计出结果;估计较大的数时,可以用“切块”的方法,即把总数平均分成几个小块,先估计出一个小块的数量,再估计出总数。
教学要求: 教学该知识点时,可以先让学生结合情境感受生活中的近似数,引导学生先自己估计,再组织学生交流寻找估计的策略。如:圈一圈,用“切块”的方法先估一部分,再推想整体数量。需要注意的是,要让学生体会到估计要有依据,要讲究策略和方法,允许学生用自己喜欢的方法估计,对于估计的结果不要求精确、统一。教师可以适当扩展估计的领域,增加估计的素材,如估计书架上的图书、体育馆的座位、报纸的字数、1千克大豆的粒数等,使学生充分体会估计策略的多样化和估计的意义。
二、知识拓展
运用分类讨论法解决估计问题。
典型例题:在所有的四位数中,你能写出最接近5000的数吗?
思路分析:在写最接近5000的四位数时,通常分为两种情况进行考虑。一种是小于5000的四位数,小于5000的四位数中最接近5000的数是4999;另一种是大于5000的四位数,大于5000的四位数中最接近5000的数是5001。
正确解答:最接近5000的四位数是4999和5001。
方法总结:在解决此类问题时,满足条件的数可能不止一个,要从多个角度进行思考。
三、知识点训练
基础训练
1. 估一估下面这段文字大约有多少个字?
泰山,是中国五岳之首,古称“岱宗”,有“中华国山”、“天下第一山”之美誉,又称东岳,中国最美的、令人震撼的十大名山之一,列中华十大名山之首。
旭日东升是泰山最迷人的奇观。拂晓,天晴气朗,万壑收暝,东方一线晨曦由灰暗变淡黄,又由淡黄变成橘红。继而,天空云朵赤紫交杂,瞬息万变。满天彩霞与地平线上的茫茫雾气连为一体,云霞雾霭相映。日轮掀开云幕,冉冉升起,宛若飘荡着的宫灯。顷刻间,金光四射,群峰尽染。然而,这只不过是一般的陆地日出,而那海上日出,更为壮观。赤轮乍启,海面半吞半吐,欲上而止,跳荡恍惚,仿佛有二日捧出。有时还能看到罕见的日珥。明代于慎行在《游泰山记》中说:“顷之,平地涌出赤盘,状如莲花,荡漾波面,而烨炜不可名状,以为日耶!又一赤盘大倍于先所见,侧立其上,若长绳左右汲挽,食顷乃定。”清代孔贞在《泰山纪胜》中称:“才一转睫,悠忽半体,若月弦就望,厥色殷红,韬光不耀,轮腾而上。少顷,日中忽如一灯吐焰,次如炬,次如瓶,次如樽,次如葫芦。上黄白,下紫赤,类薄蚀状。”
2.这个大筒大约能盛多少个乒乓球?
3.估一估,选一选。在正确的答案下面画“√”。
书架上大约有( 10 30 60 )本书。
4. 在所有的四位数中,最接近7000的数是多少?最接近10000的数是多少?
能力提升
1.估一估,填一填。
(1)微机室大约有( )台电脑。
(2)下图中大约有( )个羽毛球。
2.圈一圈,估一估。
大约( )个玻璃弹珠
一个四位数,百位上的数是千位上的数的3倍,其他数位上的数都是0,且接近4000。这个四位数是多少?
4. 在操场上走100步,估一估有多少米?走300步大约有多少米?
拓展训练
1.估一估,填一填。
2. 小明家距离超市200米,估一估,街心公园距离电影院大约多少米?
3. 下面是用火柴棒摆出的错误算式,请移动一根火柴棒使算式成立。
训练题参考答案及解析
基础训练
1. 大约有330个字。
2. 这个大筒大约能盛60个乒乓球。
3. 书架上大约有60本书。
4. 最接近7000的数是6999和7001; 最接近10000的数是9999。
能力提升
1.(1)大约50台电脑。 (2)大约100个羽毛球。
2. 大约100个玻璃弹珠。
3. 这个四位数是3900。
4. 50米,150米。
分析:走1步大约是50厘米,100步就是100个50厘米,列式100×50=5000(厘米)=50(米);300步里面有3个100步,也就是走了3个50米,列式300÷100=3 3×50=150(米)。
拓展应用
1. 200粒 400粒 50粒
2. 大约1000米
3. 正确解答:
分析:方法一 先计算出32+50的正确结果是82,再把83个位上的3变成2,可以这样移动火柴棒: 。
方法二 可以保留计算结果,因为33+50=83,所以可以把32个位上的2变成3,可以这样移动火柴棒: 。
信息窗3——万以内数的大小比较
一、知识点解读
1.近似数(初步认识)
知识点:与准确数最接近的整千、整百或几千几百、几百几十的数叫近似数,近似数用约等号“≈”连接。一个数的近似数并不唯一,要根据实际需要选择合适的近似数。
教学要求:近似数是与实际非常接近的数。教学时,先放手让学生根据已有经验说一说,然后借助数轴帮助学生直观理解一个数取近似数的方法,从而理解近似数的概念,掌握近似数的表示方法。本窗是对近似数的初步认识,不宜要求过高,近似数只要是接近整十、整百数都可以,后续还要学习用“四舍五入法”取近似数。生活中有时不需要用准确数,用近似数会更方便些。描述近似数时,不要忘记加上“大约”“大概”等标志性词语。
2.位数不同的数比较大小的方法(掌握运用)
知识点:比较位数不同的万以内的数时,根据位数的多少进行比较简单方便,位数多的数一定大于位数少的数。
教学要求:教学该知识点时,要先让学生独立思考,再交流比较大小的方法。学生可能根据位数的多少来比较,还可能根据数的组成来比较,也可能借助一个标准数来比较。对不同的方法教师都应给与及时的鼓励与肯定,使学生体验解决问题策略的多样性。
3.位数相同的数比较大小的方法(掌握运用)
知识点:比较位数相同的万以内数的大小时,先比较最高位上的数,最高位上的数大的那个数就大;如果最高位上的数相同,再依次比较下一位上的数,直到比较出大小。
教学要求:教学该知识点时,要让学生自己比较数的大小,然后交流汇报比较的方法。方法一:位数相同,从高位比起,相同数位上的数大的那个数大;方法二:用取近似数的方法比较大小。鼓励学生用自己喜欢的方法进行比较,重点引导学生理解掌握“从高位依次比较”的方法。
教学时,教师可以引导学生对万以内数大小比较的方法进行综合梳理:两个整数比较大小,位数不同时,位数多的那个数比较大;位数相同时,从高位开始依次进行比较。对于比较方法,重在结合实例进行理解,避免让学生进行机械记忆。
二、知识拓展
运用比较法解决填数问题。
典型例题:□里可以填哪些数?
□46>673 209□<2099
思路分析:□46>673中的两个数都是三位数,因为十位上4﹤7,所以百位上□里的数必须大于6,才能保证第一个数大于第二个数;209□﹤2099中的两个数都是四位数,因为千位、百位和十位上的数都相同,所以□里的数必须小于9,才能保证第一个数小于第二个数。
正确解答:第一个□里可以填7、8、9中的任意一个数;第二个□里可以填0-8中的任意一个数。
方法总结:解决此类问题时,可以利用比较数的大小的方法填数,注意不要遗漏。
三、知识点训练
基础训练
1. 下面各数的近似数是多少?选一选。
(1)上海磁悬浮列车每小时最快能行驶430千米。每小时最快大约行驶( )千米。
① 400 ② 500
(2)胶州湾海底隧道是我国目前最长的海底隧道,它分为陆上与海底两部分,其中海底部分长3950米。海底部分大约长( )米。
① 3000 ②4000
2. 小蜜蜂回家。(连一连)
3.比一比。
4. 在○里填上“>”或“<”。
500○499 2560○2650 3000○3010
828○808 1234○2143 10000○9999
能力提升
1.估一估,填一填。
(1)一辆自行车的价格是398元,大约是( )元。
(2)在一次捐书活动中,二年级共捐图书2015本,大约是( )本。
(3)双山鸭厂养鸭9760只,大约是( )只。
2.把下面各数按要求填入括号里。
999 852 640 365 847 351 1003
(1)在300和400之间的数有( )。
(2)比800大的数有( )。
(3)最接近1000的数是( )。
3. 想一想,连一连。
4. 解决问题。
五岳是中国五大名山的总称,分别是东岳泰山,高1533米;西岳华山,高2155米;南岳衡山,高1300米;北岳恒山,高2016米;中岳嵩山,高1492米。在这五座山中,哪座山最高?哪座山最低?
拓展训练
1. 在里填上合适的数。
49<496 99<1000 117<1177
13>137 853>8□3 4157>417
2. 一个三位数,个位上的数是十位上的数的3倍,十位上的数是百位上的数的3倍,这个三位数是多少?
3. 用8、6、7三个数字摆出不同的三位数,并按照从大到小的顺序排列起来。
训练题参考答案及解析
基础训练
1. (1)① (2)②
2. 接近500的数是:495、504; 接近1000的数是:988、1003、990、1004。
3. 122>97 1850<2020
4. >,<,<,>,<,>
能力提升
1. (1)400 (2)2000(3)10000
2. (1)365、351(2)999、852、847、1003(3)999
3. 新光小学1600人, 民族小学930人, 兴华小学1580人。
4. 因为2155>2016>1533>1492>1300,所以西岳华山最高,南岳衡山最低。
拓展应用
答案不唯一。依次示例:5、9、6、4、3、0。
2. 139
3. 876>867>786>768>687>678
信息窗4——整百、整千数的加减法
一、知识点解读
1.整百数加减整百数、整千数加减整千数的口算方法(掌握运用)
知识点:整百数加减整百数、整千数加减整千数的口算方法:可以先把整百、整千数看成几个百、几个千,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上相应个数的0。
教学要求:教学该知识点时,可以先复习一下100以内整十数加减整十数的口算,增加迁移的效果,然后引导学生通过自主探索、小组合作的方式学习口算方法,然后全班交流。其实,整百数(整千数)加减整百数(整千数)的口算方法就是把整百数(整千数)加减法转化为20以内的加减法。 如果学生想不到,教师可以进行引导,为后面的口算学习作铺垫。
2.几百几十加减几十的口算方法(掌握运用)
知识点:几百几十加减几十的口算方法:可以先把几百几十看成几十几个十,把几十看成几个十,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上1个0。
教学要求:教学时,由于学生已经有了整百数相加减的知识和思维基础,所以可以放手让学生自己解决,然后集体交流。对于学生出现的认知困难,可以借助计数器等直观手段帮助学生理解。
3.几千几百加减几百的口算方法(掌握运用)
知识点:几千几百加减几百的口算方法:可以先把几千几百看成几十几个百,把几百看成几个百,再相加减;也可以先把0前面的数相加减,再在得数的末尾添上2个0。
教学要求:教学时,可以让学生独立解答,然后交流。重点让学生说说口算的方法,只要方法合理即可。对于用计数单位的个数相减的口算方法,教师仍需多加关注。
二、知识拓展
运用综合法和移多补少法解决整百数的加减法问题。
典型例题:小白兔收了400根胡萝卜,小灰兔收了200根胡萝卜,小白兔给小灰兔多少根胡萝卜,它们的胡萝卜就同样多了?
思路分析:
方法一:综合法。先用加法求出胡萝卜的总数,再把总数两等分,其中的一份与小灰兔的胡萝卜数的差就是小白兔给小灰兔的胡萝卜数。
方法二:移多补少法。先求小白兔比小灰兔多多少根胡萝卜,再把多的胡萝卜两等分,其中的一份就是小白兔给小灰兔的胡萝卜数。
正确解答:
方法一:400+200=600(根),600根的一半是300根,300-200=100(根)
方法二:400-200=200(根),200根的一半是100根。所以小白兔给小灰兔100根胡萝卜,它们的胡萝卜就同样多了。
方法总结:解决此类问题时,可以先求出总数,再用总数的一半减去较小的那个数;也可以先求出两个数的差,再把差平均分成两份,其中的一份即为所求。
三、知识点训练
基础训练
1. 填一填。
(1)700+200=( ),想:( )个百加( )个百是( )个百。
(2)1200-300=( ),想:( )个百减( )个百是( )个百。
(3)3000+600=( ),想:( )个百加( )个百是( )个百。
2. 算一算。
400+800= 8000-4000= 900+60= 230+40=
2000-400= 9000-4500= 4300+600= 1100-500=
2800+500= 5300-300= 4000+90= 7000-3000=
3. 在○里填上“>”“<”或“=”。
400+700○2000-800 1400-700○2700-500 6200-800○3200+2000
4600-800○3200+300 1500+600○7200-100 2700-400○1600+700
4. 解决问题。
1路公交车今天运送乘客1300人,2路公交车今天运送乘客900人,3路公交车今天运送乘客700人。
(1)1路公交车比3路公交车多运送乘客多少人?
(2)3辆公交车一共运送乘客多少人?
能力提升
1.把400、500、600、700分别填入括号内,使等式成立。
( )+( )-( )=( )
2. ●-★=1000 ●-★-★=700
●=( ) ★=()
3. 一根绳子长600米,第一次用去了100米,第二次用去了320米,这根绳子短了多少米?
4. 妈妈有1000元,爸爸有400元,妈妈给爸爸多少元后,两人的钱数就同样多了?
拓展训练
甲乙丙三个数的和是1000,甲乙两个数的和是500,乙丙两数的和是700,甲乙丙三数分别是多少?
2. 在下面的○里填上不同的整百数,使每条边上三个数的和都是1000。
3.把一根5米长的竹竿插到井底,取出后又把另一端插到井底。这时,竹竿中间有长60厘米的部分没有湿。你知道井水有多深吗?
训练题参考答案及解析
基础训练
1. (1)900,7,2,9 (2)900,12,3,9(3)3600,30,6,36
2. 1200 4000 960 270
1600 4500 4900 600
3300 5000 4090 4000
3. <,<,>,>,<,=
4.(1)1300-700=600(人),1路公交车比3路公交车多运送乘客600人。
(2)1300+900+700=2900(人),3辆公交车一共运送乘客2900人。
能力提升
1. 答案不唯一。示例:400+700-600=500
2. ●=1300 ★=300
3. 100+320=420(米),这根绳子短了420米。
4. 1000-400=600(元),600元的一半是300元,因此妈妈给爸爸300元后,两人的钱数就同样多了。
拓展应用
1. 乙数:500+700=1200,1200-1000=200
甲数:500-200=300
丙数:700-200=500
答案不唯一。示例:
3. 220厘米。
分析:可以借助画图和学具操作帮助理解。竹竿的长度被分成了3部分,分别是顺着插入井底被浸湿的部分,倒着插入井底被浸湿的部分、中间没有被浸湿的部分。其中两端浸湿部分是相等的,中间没有浸湿的部分是60厘米。列式:5米=500厘米,500-60=440(厘米),440÷2=220(厘米)
信息窗5——估计
一、知识点解读
估计万以内的数(掌握运用)
知识点:估计在生活中应用广泛,包括对长度、高度、质量、时间等的估计。估计时要有根据、讲方法,尽量让估出的数接近准确数。估计的方法有多种,可以凭借经验估计,也可以先数出一部分或圈出一部分,再估计出结果;估计较大的数时,可以用“切块”的方法,即把总数平均分成几个小块,先估计出一个小块的数量,再估计出总数。
教学要求: 教学该知识点时,可以先让学生结合情境感受生活中的近似数,引导学生先自己估计,再组织学生交流寻找估计的策略。如:圈一圈,用“切块”的方法先估一部分,再推想整体数量。需要注意的是,要让学生体会到估计要有依据,要讲究策略和方法,允许学生用自己喜欢的方法估计,对于估计的结果不要求精确、统一。教师可以适当扩展估计的领域,增加估计的素材,如估计书架上的图书、体育馆的座位、报纸的字数、1千克大豆的粒数等,使学生充分体会估计策略的多样化和估计的意义。
二、知识拓展
运用分类讨论法解决估计问题。
典型例题:在所有的四位数中,你能写出最接近5000的数吗?
思路分析:在写最接近5000的四位数时,通常分为两种情况进行考虑。一种是小于5000的四位数,小于5000的四位数中最接近5000的数是4999;另一种是大于5000的四位数,大于5000的四位数中最接近5000的数是5001。
正确解答:最接近5000的四位数是4999和5001。
方法总结:在解决此类问题时,满足条件的数可能不止一个,要从多个角度进行思考。
三、知识点训练
基础训练
1. 估一估下面这段文字大约有多少个字?
泰山,是中国五岳之首,古称“岱宗”,有“中华国山”、“天下第一山”之美誉,又称东岳,中国最美的、令人震撼的十大名山之一,列中华十大名山之首。
旭日东升是泰山最迷人的奇观。拂晓,天晴气朗,万壑收暝,东方一线晨曦由灰暗变淡黄,又由淡黄变成橘红。继而,天空云朵赤紫交杂,瞬息万变。满天彩霞与地平线上的茫茫雾气连为一体,云霞雾霭相映。日轮掀开云幕,冉冉升起,宛若飘荡着的宫灯。顷刻间,金光四射,群峰尽染。然而,这只不过是一般的陆地日出,而那海上日出,更为壮观。赤轮乍启,海面半吞半吐,欲上而止,跳荡恍惚,仿佛有二日捧出。有时还能看到罕见的日珥。明代于慎行在《游泰山记》中说:“顷之,平地涌出赤盘,状如莲花,荡漾波面,而烨炜不可名状,以为日耶!又一赤盘大倍于先所见,侧立其上,若长绳左右汲挽,食顷乃定。”清代孔贞在《泰山纪胜》中称:“才一转睫,悠忽半体,若月弦就望,厥色殷红,韬光不耀,轮腾而上。少顷,日中忽如一灯吐焰,次如炬,次如瓶,次如樽,次如葫芦。上黄白,下紫赤,类薄蚀状。”
2.这个大筒大约能盛多少个乒乓球?
3.估一估,选一选。在正确的答案下面画“√”。
书架上大约有( 10 30 60 )本书。
4. 在所有的四位数中,最接近7000的数是多少?最接近10000的数是多少?
能力提升
1.估一估,填一填。
(1)微机室大约有( )台电脑。
(2)下图中大约有( )个羽毛球。
2.圈一圈,估一估。
大约( )个玻璃弹珠
一个四位数,百位上的数是千位上的数的3倍,其他数位上的数都是0,且接近4000。这个四位数是多少?
4. 在操场上走100步,估一估有多少米?走300步大约有多少米?
拓展训练
1.估一估,填一填。
2. 小明家距离超市200米,估一估,街心公园距离电影院大约多少米?
3. 下面是用火柴棒摆出的错误算式,请移动一根火柴棒使算式成立。
训练题参考答案及解析
基础训练
1. 大约有330个字。
2. 这个大筒大约能盛60个乒乓球。
3. 书架上大约有60本书。
4. 最接近7000的数是6999和7001; 最接近10000的数是9999。
能力提升
1.(1)大约50台电脑。 (2)大约100个羽毛球。
2. 大约100个玻璃弹珠。
3. 这个四位数是3900。
4. 50米,150米。
分析:走1步大约是50厘米,100步就是100个50厘米,列式100×50=5000(厘米)=50(米);300步里面有3个100步,也就是走了3个50米,列式300÷100=3 3×50=150(米)。
拓展应用
1. 200粒 400粒 50粒
2. 大约1000米
3. 正确解答:
分析:方法一 先计算出32+50的正确结果是82,再把83个位上的3变成2,可以这样移动火柴棒: 。
方法二 可以保留计算结果,因为33+50=83,所以可以把32个位上的2变成3,可以这样移动火柴棒: 。
