人教版七年级下册7.2.2 用坐标表示平移导学案
文档属性
| 名称 | 人教版七年级下册7.2.2 用坐标表示平移导学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 342.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览

文档简介
第七章 平面直角坐标系
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
学习目标:1.进一步理解图形平移的内涵,会写出平移前后图形上任一点的坐标,给出变化的点的坐标能够知道点的移动路径与距离.
2.通过观察、分析、操作等实践活动,使学生掌握在坐标系中描述图形平移的方法.
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
重点:掌握用点的坐标的变化规律来描述图形平移的过程.
难点:根据图形的平移过程,探索、归纳出点的坐标的变化规律.
一、知识链接
1.什么是图形的平移?
2.图形的平移有哪些性质?
二、新知预习
平移规律:
(1)点的平移:在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点 (或 );将点(x,y)向上(或下)平移b个单位长度,可以得到对应点 (或) .
(2)图形的平移:一般的,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正实数a,相应的新图形就是 ;
如果把它各个点的纵坐标都加(或减去)一个正实数a,相应的新图形就是 .
三、自学自测
1.已知点A(2,-3),若将点A向左平移3个单位得到点B,则点B的坐标是 ,若将点A向上平移4个单位得到点C,则点C的坐标是 .
2.已知正方形的一个顶点A(-4,2),把此正方形向上平移2个单位长度,再向左平移3个单位长度,此时点A的坐标变成 .
四、我的疑惑
______________________________________________________________________________________________________________________________________________________
要点探究
探究点1:平面直角坐标系中点的平移
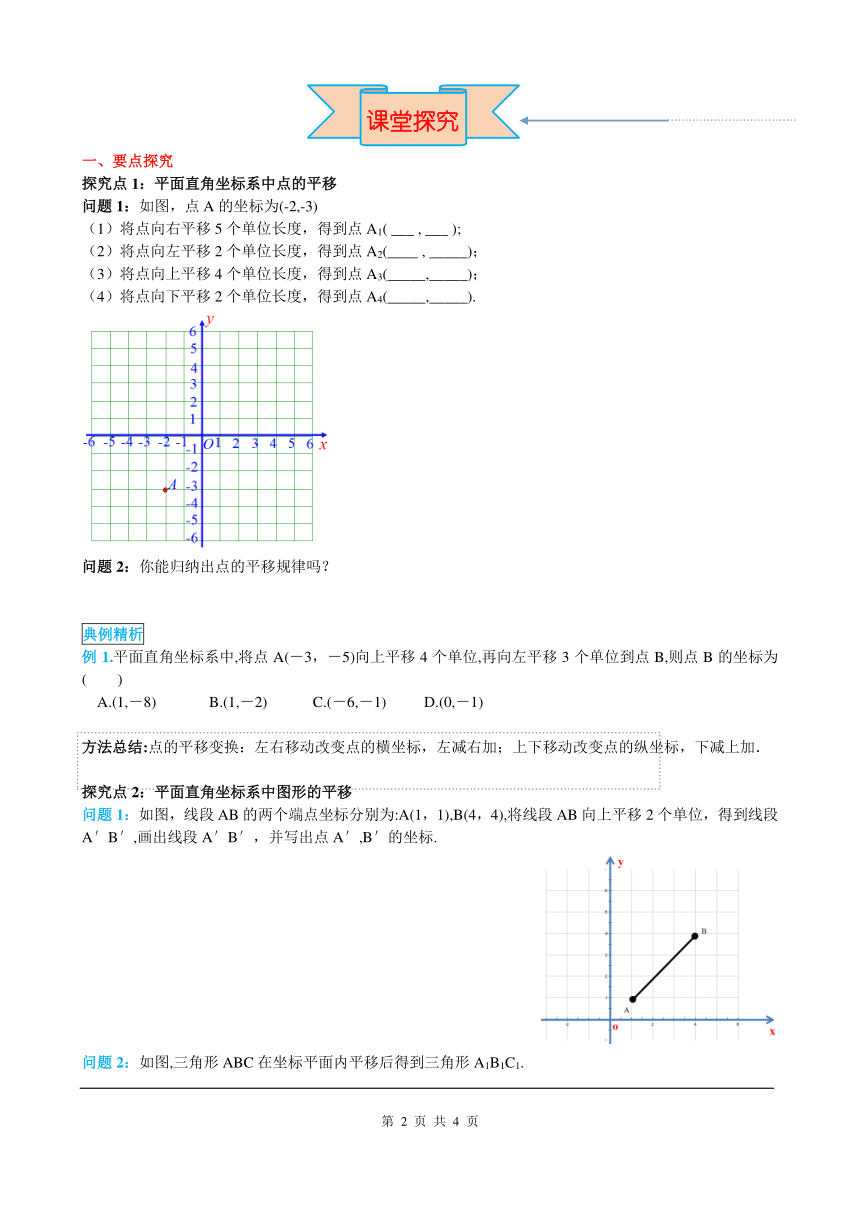
问题1:如图,点A的坐标为(-2,-3)
(1)将点向右平移5个单位长度,得到点A1( ___ , ___ );
(2)将点向左平移2个单位长度,得到点A2(____ , _____);
(3)将点向上平移4个单位长度,得到点A3(_____,_____);
(4)将点向下平移2个单位长度,得到点A4(_____,_____).
问题2:你能归纳出点的平移规律吗?
典例精析
例1.平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
方法总结:点的平移变换:左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.
探究点2:平面直角坐标系中图形的平移
问题1:如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),将线段AB向上平移2个单位,得到线段A′B′,画出线段A′B′,并写出点A′,B′的坐标.
问题2:如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
(1)移动的方向怎样?
(2)写出三角形ABC与三角形A1B1C1各
点的坐标,它们有怎样的变化?
(3)如果三角形A1B1C1向下平移4个单位,得到三角形 A2B2C2,写出各点的坐标,它们有怎样的变化?
(4)三角形 ABC能否在坐标平面内直接平移后得到三角形 A2B2C2?
问题3:通过对以上问题的探讨,你能说出图形平移的规律吗?
总结归纳:
典例精析
例2.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角形A1B1C1,并写出点A、C、A1、C1的坐标;
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
二、课堂小结
点(或图形)在坐标系中的平移
沿x轴平移
纵坐标不变,向右平移,横坐标加上一个正数;向左平移,横坐标减去一个正数
沿y轴平移
横坐标不变,向上平移,纵坐标加上一个正数;向下平移,纵坐标减去一个正数
1.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标为______.
2.将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标
为______.
6.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个
单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
7.(1)已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为____________.
8.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),
将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
7.2 坐标方法的简单应用
7.2.2 用坐标表示平移
学习目标:1.进一步理解图形平移的内涵,会写出平移前后图形上任一点的坐标,给出变化的点的坐标能够知道点的移动路径与距离.
2.通过观察、分析、操作等实践活动,使学生掌握在坐标系中描述图形平移的方法.
3.激情投入,善于发现问题和提出问题,感受学习数学的乐趣.
重点:掌握用点的坐标的变化规律来描述图形平移的过程.
难点:根据图形的平移过程,探索、归纳出点的坐标的变化规律.
一、知识链接
1.什么是图形的平移?
2.图形的平移有哪些性质?
二、新知预习
平移规律:
(1)点的平移:在平面直角坐标系中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点 (或 );将点(x,y)向上(或下)平移b个单位长度,可以得到对应点 (或) .
(2)图形的平移:一般的,在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正实数a,相应的新图形就是 ;
如果把它各个点的纵坐标都加(或减去)一个正实数a,相应的新图形就是 .
三、自学自测
1.已知点A(2,-3),若将点A向左平移3个单位得到点B,则点B的坐标是 ,若将点A向上平移4个单位得到点C,则点C的坐标是 .
2.已知正方形的一个顶点A(-4,2),把此正方形向上平移2个单位长度,再向左平移3个单位长度,此时点A的坐标变成 .
四、我的疑惑
______________________________________________________________________________________________________________________________________________________
要点探究
探究点1:平面直角坐标系中点的平移
问题1:如图,点A的坐标为(-2,-3)
(1)将点向右平移5个单位长度,得到点A1( ___ , ___ );
(2)将点向左平移2个单位长度,得到点A2(____ , _____);
(3)将点向上平移4个单位长度,得到点A3(_____,_____);
(4)将点向下平移2个单位长度,得到点A4(_____,_____).
问题2:你能归纳出点的平移规律吗?
典例精析
例1.平面直角坐标系中,将点A(-3,-5)向上平移4个单位,再向左平移3个单位到点B,则点B的坐标为( )
A.(1,-8) B.(1,-2) C.(-6,-1) D.(0,-1)
方法总结:点的平移变换:左右移动改变点的横坐标,左减右加;上下移动改变点的纵坐标,下减上加.
探究点2:平面直角坐标系中图形的平移
问题1:如图,线段AB的两个端点坐标分别为:A(1,1),B(4,4),将线段AB向上平移2个单位,得到线段A′B′,画出线段A′B′,并写出点A′,B′的坐标.
问题2:如图,三角形ABC在坐标平面内平移后得到三角形A1B1C1.
(1)移动的方向怎样?
(2)写出三角形ABC与三角形A1B1C1各
点的坐标,它们有怎样的变化?
(3)如果三角形A1B1C1向下平移4个单位,得到三角形 A2B2C2,写出各点的坐标,它们有怎样的变化?
(4)三角形 ABC能否在坐标平面内直接平移后得到三角形 A2B2C2?
问题3:通过对以上问题的探讨,你能说出图形平移的规律吗?
总结归纳:
典例精析
例2.如图,在平面直角坐标系中,P(a,b)是三角形ABC的边AC上一点,三角形ABC经平移后点P的对应点为P1(a+6,b+2).
(1)请画出上述平移后的三角形A1B1C1,并写出点A、C、A1、C1的坐标;
(2) 求出以A、C、A1、C1为顶点的四边形的面积.
二、课堂小结
点(或图形)在坐标系中的平移
沿x轴平移
纵坐标不变,向右平移,横坐标加上一个正数;向左平移,横坐标减去一个正数
沿y轴平移
横坐标不变,向上平移,纵坐标加上一个正数;向下平移,纵坐标减去一个正数
1.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标为______.
2.将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
3.将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标
为______.
6.在平面直角坐标系中,将点A(1,﹣2)向上平移3个单位长度,再向左平移2个
单位长度,得到点A′,则点A′的坐标是( )
A.(﹣1,1) B.(﹣1,﹣2) C.(﹣1,2) D.(1,2)
7.(1)已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为____________.
8.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),
将三角形ABC作同样的平移得到三角形A1B1C1.求A1、B1、C1的坐标.
