人教版数学八年级下册:18.1.3 三角形的中位线定理 课件 (共22张PPT)
文档属性
| 名称 | 人教版数学八年级下册:18.1.3 三角形的中位线定理 课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 706.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
平行四边形的判定
第 3 课 时
小学庆“六一”文艺汇演主持词
(女)尊敬的各位领导、老师,
(男)爷爷、奶奶
(女)叔叔、阿姨
(合)大家上午好!
(男)六月的文庄小学,气候宜人,鲜花盛开。
(女)六月的文庄小学,草长莺飞,生机盎然。
(男)伴着花的芬芳,披着节日的盛装,
(女)“六一”,这个属于我们的节日,又来到了我们的身旁。
(男)在这特殊的日子里,我们的心充满感激,
(女)感谢园丁们的辛勤培育,
感谢在座的家长们.
(男)是你们赋予我们搏击长空的力量,
(女)是你们给予我们战胜困难的勇气。
(男)今天,我们代表全校少年儿童来向您们汇报,
(女)我们正在奋发努力,建设美丽强大的祖国,我们有能力把重担挑起。
(男)下面我宣布:
(合)文庄小学庆祝“六一”国际儿童节联欢会,现在开始!
(男) 群鸽起舞,大雁飞翔,
美丽的花环寄托着我们对未来的畅想,
(女)请欣赏一年级小朋友带来的歌曲《春天在哪里》
(男)快乐和甜蜜与我们相伴,阳光洒满幸福的童年
(女)接下来,请欣赏文庄幼儿园大班的小朋友为我们带来的舞蹈《咚巴拉》
(男)小朋友们的表演真是精彩,接下来请欣赏二年级同学带来的舞蹈《唱五环》
(男)你们看,那边走来了一群穿
A
B
C
D
E
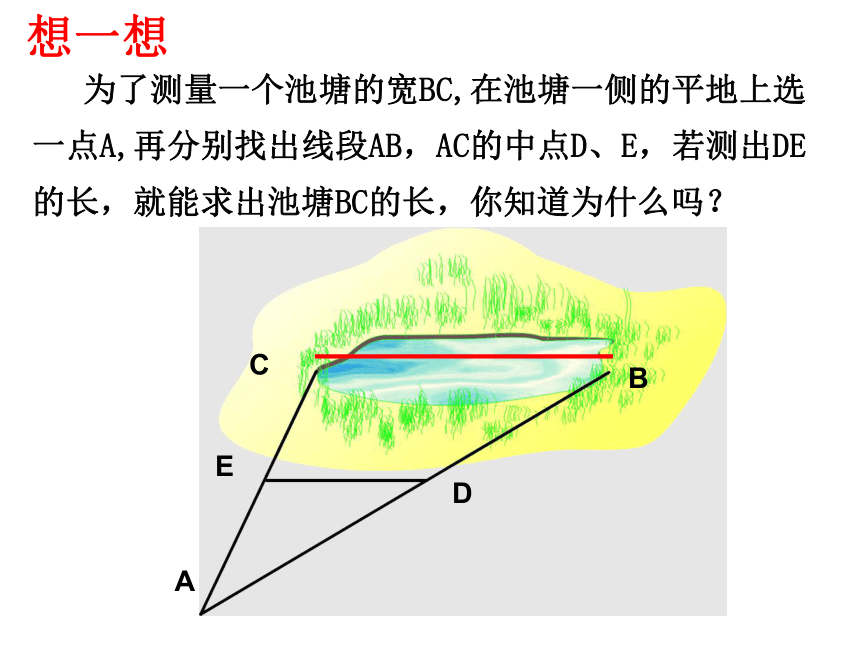
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
想一想
三角形的中位线
学习目标:
1.三角形的中位线的定义
2.三角形的中位线的性质
3.发现中位线,运用中位线的性质
4.构造中位线,运用中位线的性质
A
B
C
D
E
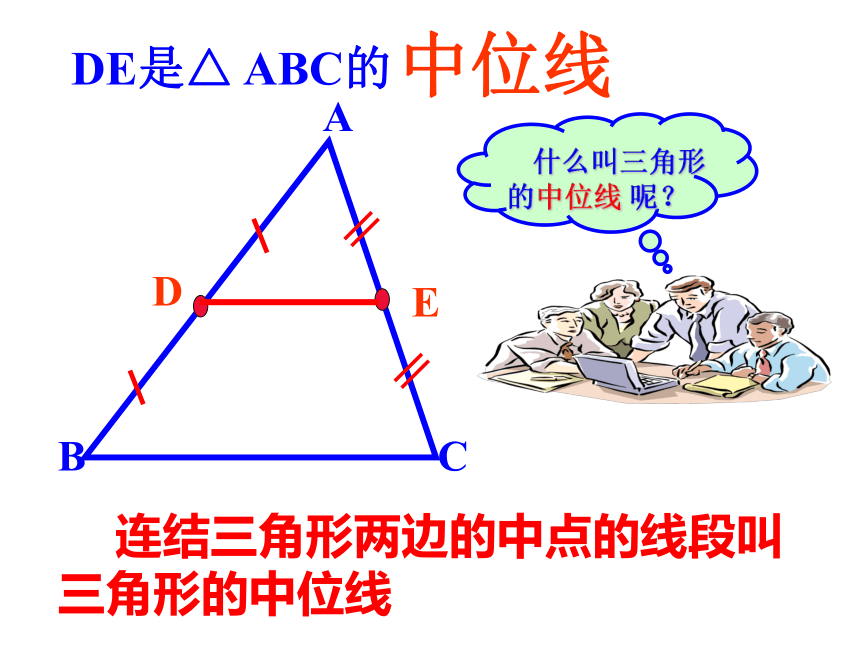
DE是△ ABC的
中位线
什么叫三角形的中位线 呢?
连结三角形两边的中点的线段叫
三角形的中位线
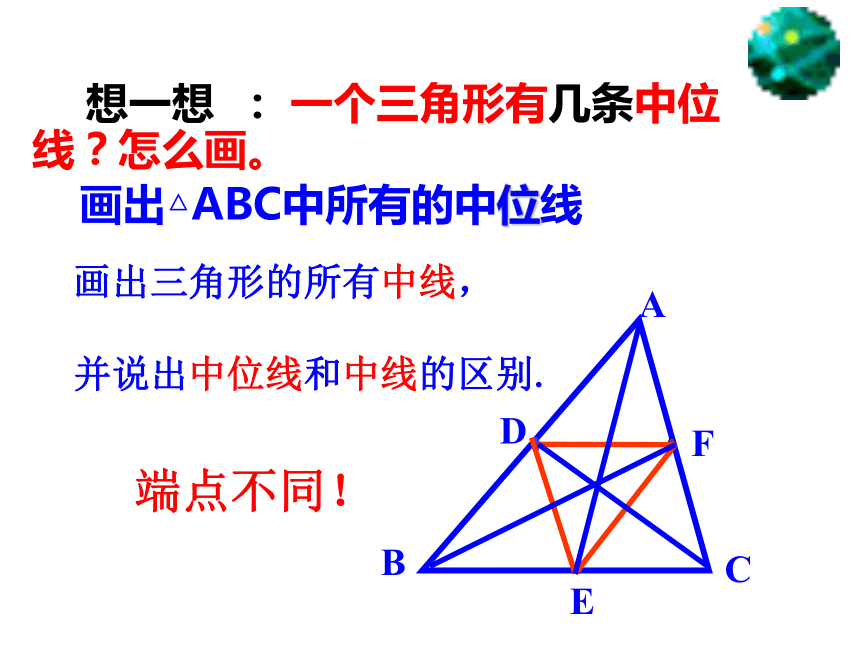
想一想 : 一个三角形有几条中位线?怎么画。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
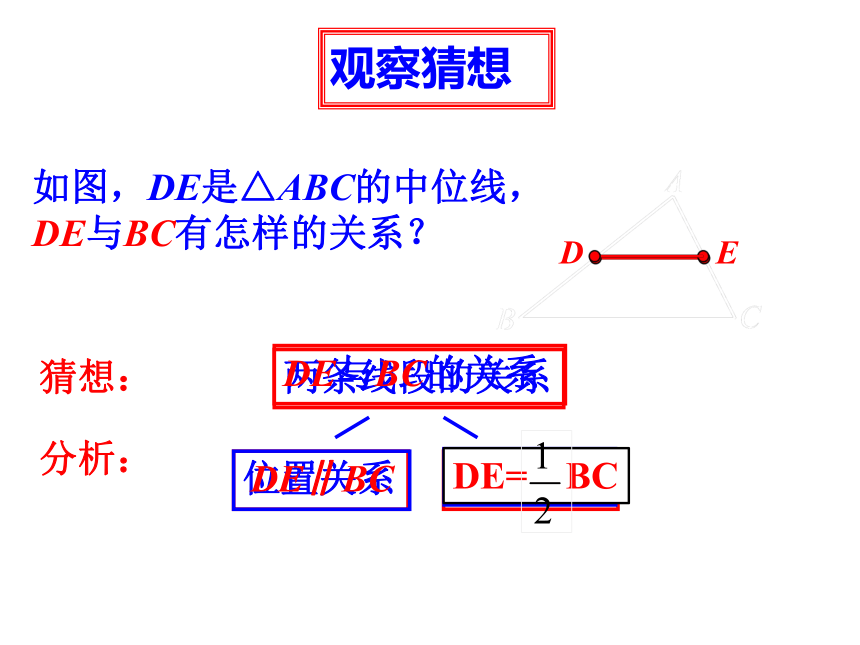
观察猜想
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
DE= BC
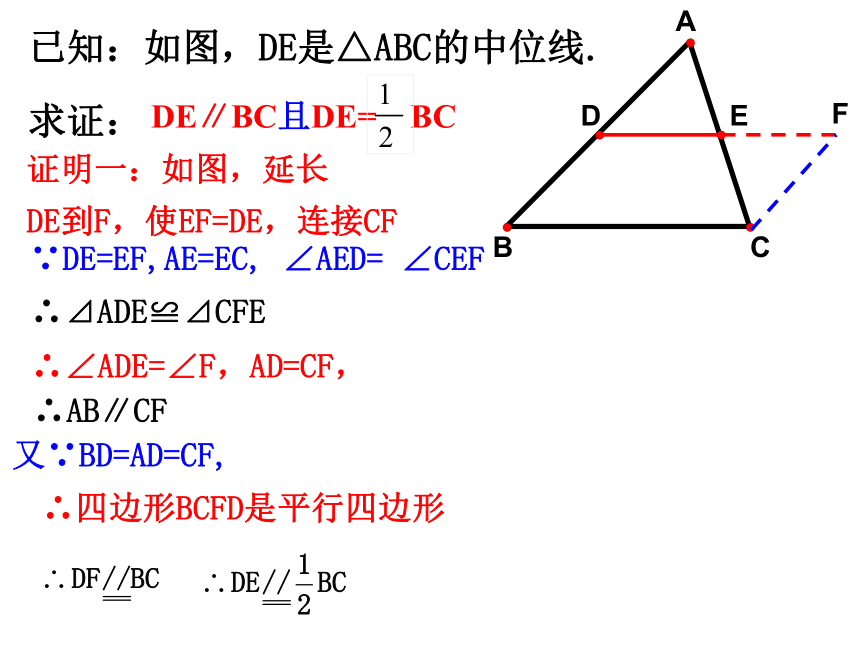
证明一:如图,延长
DE到F,使EF=DE,连接CF
∴∠ADE=∠F,AD=CF,
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
A
B
C
D
E
F
∵DE=EF,AE=EC, ∠AED= ∠CEF
∴⊿ADE≌⊿CFE
已知:如图,DE是△ABC的中位线.
求证:
DE∥BC且DE= BC
A
B
C
E
D
F
证法二:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形?
已知:如图,DE是△ABC的中位线.
求证:
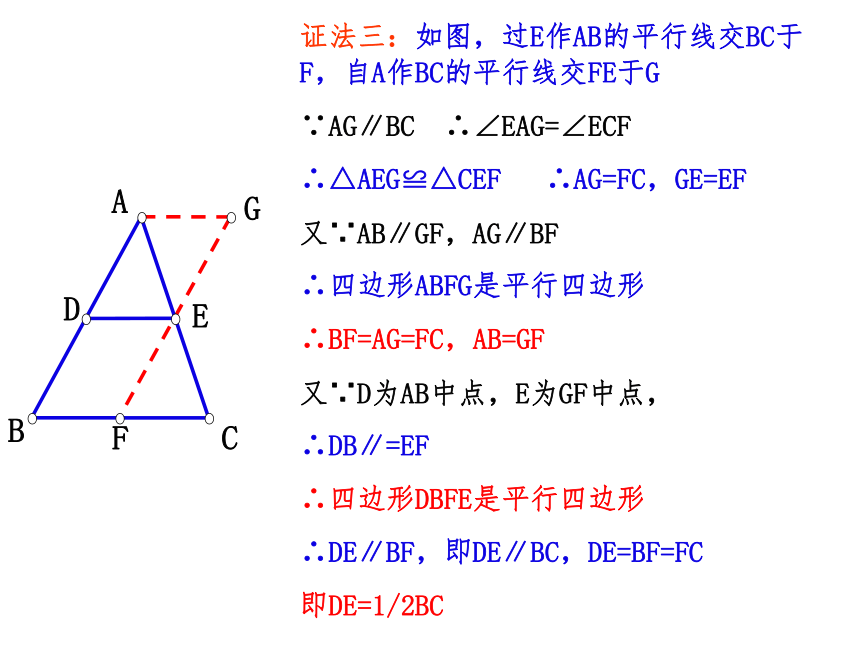
证法三:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC ∴∠EAG=∠ECF
∴△AEG≌△CEF ∴AG=FC,GE=EF
又∵AB∥GF,AG∥BF
∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又∵D为AB中点,E为GF中点,
∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BC
A
B
C
E
D
F
G
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线性质定理:
A
B
C
D
E
∵DE是△ABC的中位线,
符号语言:
有何作用?
( ∵AD=BD, AE=CE )
1、证明线段平行
2、 证明线段成倍分关系
∴DE∥BC且DE= BC
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
若DE=30米,则BC=?
想一想
若DE无法测量呢?
A
B
C
D
E
如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。
F
由此可知:……
知识拓展
DE∥BC且DE= BC
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB
知识拓展
(1)三角形三条中位线把三角形分成的四个三角形 .
(2)三角形三条中位线所构成的三角形的面积等于原三角形面积的
A
B
C
D
E
F
(3)图中有 平行四边形
三个
全等
四分之一
1.如图1:在△ABC中,DE是中位线
(1)若∠CDE=60°,
则∠B= 度,为什么?
(2)若AB=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别是各边中点AB=6cm,AC=8cm,BC=10cm,则△DEF的周长= cm
60
4
12
图1
A
B
C
D。
。E
图2
B
A
C
D 。
。E
。F
练习一
例1:如图,D、E分别是△ABC的边AB、AC的中
点,点O是△ABC内部任意一点,连接OB、
OC,点G、F分别是OB、OC的中点,顺次
连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
A
B
C
G
F
E
D
O
∴四边形DGFE是□
证明:
练习二
如图,D、 E 、F分别是△ABC三边中点, AH⊥BC于H.
求证:DF=EH
A
B
C
H
F
D
E
例2: 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证四边形EFGH是平行四边形.
证明:连接AC
在△DAC中,∵AH=HD,CG=GD,
∴HG∥AC,HG= AC.
同理可得EF∥AC,EF= AC.
∴HG∥EF,且HG=EF.
∴四边形EFGH是平行四边形.
练习三
已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN,D,E,F分别是MB,BC,CN的中点,连结DE,FE,
求证:DE=FE
A
N
M
F
E
D
C
B
例3:如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:
H
G
O
F
E
A
D
B
C
AC=BD
OG=OH
M
则ME=MF
1.三角形的中位线的定义:.
课堂小结
2.三角形中位线性质定理
这节课学习了什么?
三角形中位线定理应用:
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 一半
提供了一个新的途径
方法点拨:在处理问题时,要求同时出现三角形及中位线
1.有中点要想中位线,发现中位线
2.有中点连线而无三角形,要作辅助线产生三角形构造中位线
3.有三角形而无中位线,要连结两边中点构造中位线
4.由已知中点得到中位线没有用,另取中点构造中位线
平行四边形的判定
第 3 课 时
小学庆“六一”文艺汇演主持词
(女)尊敬的各位领导、老师,
(男)爷爷、奶奶
(女)叔叔、阿姨
(合)大家上午好!
(男)六月的文庄小学,气候宜人,鲜花盛开。
(女)六月的文庄小学,草长莺飞,生机盎然。
(男)伴着花的芬芳,披着节日的盛装,
(女)“六一”,这个属于我们的节日,又来到了我们的身旁。
(男)在这特殊的日子里,我们的心充满感激,
(女)感谢园丁们的辛勤培育,
感谢在座的家长们.
(男)是你们赋予我们搏击长空的力量,
(女)是你们给予我们战胜困难的勇气。
(男)今天,我们代表全校少年儿童来向您们汇报,
(女)我们正在奋发努力,建设美丽强大的祖国,我们有能力把重担挑起。
(男)下面我宣布:
(合)文庄小学庆祝“六一”国际儿童节联欢会,现在开始!
(男) 群鸽起舞,大雁飞翔,
美丽的花环寄托着我们对未来的畅想,
(女)请欣赏一年级小朋友带来的歌曲《春天在哪里》
(男)快乐和甜蜜与我们相伴,阳光洒满幸福的童年
(女)接下来,请欣赏文庄幼儿园大班的小朋友为我们带来的舞蹈《咚巴拉》
(男)小朋友们的表演真是精彩,接下来请欣赏二年级同学带来的舞蹈《唱五环》
(男)你们看,那边走来了一群穿
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
想一想
三角形的中位线
学习目标:
1.三角形的中位线的定义
2.三角形的中位线的性质
3.发现中位线,运用中位线的性质
4.构造中位线,运用中位线的性质
A
B
C
D
E
DE是△ ABC的
中位线
什么叫三角形的中位线 呢?
连结三角形两边的中点的线段叫
三角形的中位线
想一想 : 一个三角形有几条中位线?怎么画。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线,
并说出中位线和中线的区别.
D
E
F
端点不同!
观察猜想
如图,DE是△ABC的中位线,
DE与BC有怎样的关系?
D
E
两条线段的关系
位置关系
数量关系
分析:
DE与BC的关系
猜想:
DE∥BC
?
DE= BC
证明一:如图,延长
DE到F,使EF=DE,连接CF
∴∠ADE=∠F,AD=CF,
∴AB∥CF
又∵BD=AD=CF,
∴四边形BCFD是平行四边形
A
B
C
D
E
F
∵DE=EF,AE=EC, ∠AED= ∠CEF
∴⊿ADE≌⊿CFE
已知:如图,DE是△ABC的中位线.
求证:
DE∥BC且DE= BC
A
B
C
E
D
F
证法二:延长DE到点F,使EF=DE, 连结AF、CF、CD
∵AE=EC∴DE=EF
∴四边形ADCF是平行四边形 ∴AD∥=FC
又D为AB中点,∴DB∥=FC
所以,四边形BCFD是平行四边形?
已知:如图,DE是△ABC的中位线.
求证:
证法三:如图,过E作AB的平行线交BC于F,自A作BC的平行线交FE于G
∵AG∥BC ∴∠EAG=∠ECF
∴△AEG≌△CEF ∴AG=FC,GE=EF
又∵AB∥GF,AG∥BF
∴四边形ABFG是平行四边形
∴BF=AG=FC,AB=GF
又∵D为AB中点,E为GF中点,
∴DB∥=EF
∴四边形DBFE是平行四边形
∴DE∥BF,即DE∥BC,DE=BF=FC
即DE=1/2BC
A
B
C
E
D
F
G
三角形的中位线平行于三角形的第三边,且等于第三边的一半。
三角形中位线性质定理:
A
B
C
D
E
∵DE是△ABC的中位线,
符号语言:
有何作用?
( ∵AD=BD, AE=CE )
1、证明线段平行
2、 证明线段成倍分关系
∴DE∥BC且DE= BC
A
B
C
D
E
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
若DE=30米,则BC=?
想一想
若DE无法测量呢?
A
B
C
D
E
如图,D、E、F分别是△ABC的三边的中点,那么,DE、DF、EF都是△ABC的中位线。
F
由此可知:……
知识拓展
DE∥BC且DE= BC
同理:DF∥AC且DF= AC;
EF∥AB且EF= AB
知识拓展
(1)三角形三条中位线把三角形分成的四个三角形 .
(2)三角形三条中位线所构成的三角形的面积等于原三角形面积的
A
B
C
D
E
F
(3)图中有 平行四边形
三个
全等
四分之一
1.如图1:在△ABC中,DE是中位线
(1)若∠CDE=60°,
则∠B= 度,为什么?
(2)若AB=8cm,
则DE= cm,为什么?
2.如图2:在△ABC中,D、E、F分别是各边中点AB=6cm,AC=8cm,BC=10cm,则△DEF的周长= cm
60
4
12
图1
A
B
C
D。
。E
图2
B
A
C
D 。
。E
。F
练习一
例1:如图,D、E分别是△ABC的边AB、AC的中
点,点O是△ABC内部任意一点,连接OB、
OC,点G、F分别是OB、OC的中点,顺次
连接点D、G、F、E.
求证:四边形DGFE是平行四边形.
A
B
C
G
F
E
D
O
∴四边形DGFE是□
证明:
练习二
如图,D、 E 、F分别是△ABC三边中点, AH⊥BC于H.
求证:DF=EH
A
B
C
H
F
D
E
例2: 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证四边形EFGH是平行四边形.
证明:连接AC
在△DAC中,∵AH=HD,CG=GD,
∴HG∥AC,HG= AC.
同理可得EF∥AC,EF= AC.
∴HG∥EF,且HG=EF.
∴四边形EFGH是平行四边形.
练习三
已知:如图,△ABC是锐角三角形。分别以AB,AC为边向外侧作等边三角形ABM和等边三角形CAN,D,E,F分别是MB,BC,CN的中点,连结DE,FE,
求证:DE=FE
A
N
M
F
E
D
C
B
例3:如图,在四边形ABCD中,对角线AC,BD相交于点O,且 ,E,F分别是AB,CD的中点,EF分别交BD,AC于点G , H。
求证:
H
G
O
F
E
A
D
B
C
AC=BD
OG=OH
M
则ME=MF
1.三角形的中位线的定义:.
课堂小结
2.三角形中位线性质定理
这节课学习了什么?
三角形中位线定理应用:
⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 一半
提供了一个新的途径
方法点拨:在处理问题时,要求同时出现三角形及中位线
1.有中点要想中位线,发现中位线
2.有中点连线而无三角形,要作辅助线产生三角形构造中位线
3.有三角形而无中位线,要连结两边中点构造中位线
4.由已知中点得到中位线没有用,另取中点构造中位线
