青岛版六三制数学六年级下册第2单元知识点及典型题目训练二(含答案)
文档属性
| 名称 | 青岛版六三制数学六年级下册第2单元知识点及典型题目训练二(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-22 00:00:00 | ||
图片预览





文档简介
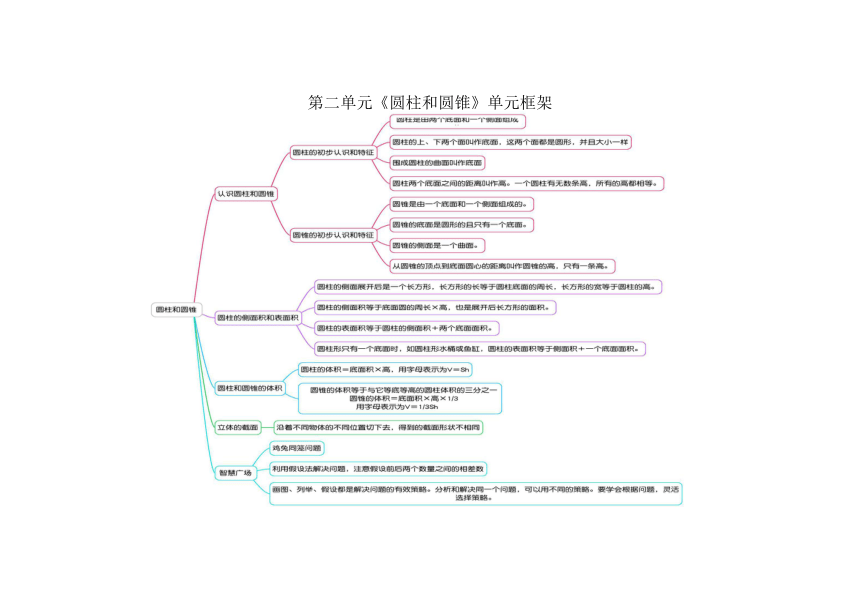
第二单元《圆柱和圆锥》单元框架
信息窗2——圆柱的侧面积和表面积
一、知识点解读
1. 圆柱的侧面积计算公式(掌握运用)
知识点:圆柱的侧面积计算公式:圆柱的侧面积=底面周长×高,用字母表示为:S侧=Ch。
教学要求: 该知识点是学习圆柱侧面积计算公式的推导,是在掌握了长方形面积和圆的周长的的基础上推导出来的。学习时,可联系以前学过的平面图形面积公式的推导方法,把一个圆柱沿着高剪开,展开后是个长方形,长方形的长等于圆柱底面的周长,长方形的宽就是圆柱的高,由长方形的面积计算公式推导出圆柱侧面积计算公式。
2.圆柱的表面积的计算公式(掌握运用)
知识点:圆柱的表面积的计算公式:圆柱的侧面积+底面积×2,用字母表示为:S表=S侧+2S底。
教学要求:该知识点是认识圆柱的表面积以及学习圆柱的表面积计算方法,是在掌握圆柱的侧面积和圆的面积计算方法的基础上学习的。学习时,可在操作的过程中理解圆柱表面积的意义,并感悟圆柱表面积的计算方法。
二、知识拓展
求圆柱的表面积要具体情况具体分析,求用料多少,一般采用“进一法”取近似值,以保证原材料够用。
三、知识点训练
基础训练
1.
圆柱的侧面展开后是一个________,这个长方形的长等于圆柱的________,长方形的宽等于圆柱的________。因此圆柱的侧面积= ________________。
2. 圆柱的( )面积加上( )的面积,就是圆柱的表面积。
3. 求易拉罐上商标纸的面积,实际上是求( )。
4. 做一个油桶所需铁皮面积,实际上是求( )。
5. 圆柱的底面周长是2.1米,高0.9米。这个圆柱的侧面积是( )平方米。
能力提升
1. 一个圆柱底面直径是6dm,高是3dm,求它的表面积。
2. 一个圆柱,它的高是8厘米,侧面积是200.96平方厘米,它的底面积是( )。
3. 制作一个高14厘米,底面直径是5厘米的饮料罐,至少需要多少铁皮?(得数保留整数 )
4. 制作一个底面周长是25.12厘米的笔筒,大约需要多少平方厘米的材料?(得数保留整数 )
5. 一台压路机的前轮是圆柱形,轮宽2米,直径为1.2米,前轮滚动一周,压过的路是多少平方米?
拓展应用
1. 圆柱的底面半径扩大到原来的2倍,高不变,它的侧面积扩大到原来的( )倍。
2. 一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加多少平方分米?
3. 用铁皮做8节同样大小的圆柱形通风管,每节的直径是20厘米,长40厘米,一共需要多少平方厘米的铁皮?
4.学校走廊有5根相同的圆形木桩,底面周长是9.42分米,高是4米,给这些木桩涂油漆,如果每平方米用油漆25克,一个需要多少千克油漆?
5. 一根圆柱形的木料,截去10厘米长的一小段后,剩下圆柱形木料的表面积比原来减少了62.8平方厘米。这根木料的底面积是多少平方厘米?
训练题参考答案及解析
基础训练
1. 长方形 底面周长 高 底面周长×高
2. 侧 2个底面
3. 圆柱的侧面积
4. 圆柱的表面积
5. 1.89
能力提升
1.113.04平方分米。
解析:因为圆柱的表面积=圆柱的侧面积+底面积×2,所以先求出底面的半径,再根据公式列式计算即可。
答案为6÷2=3(分米),3.14×6×3+3.14×3?×2=18.84×3+28.26×2=56.52+56.52=113.04(平方分米)
2.50.24平方厘米
解析:要求它的底面积,需要求出圆柱的底面半径,根据圆柱的侧面积=2πrh,可得r=侧面积÷(2πh),列式为:200.96÷(3.14×2×8)=200.96÷50.24=4(厘米),3.14×4?=3.14×16=50.24(平方厘米)
3.260平方厘米。
解析:根据图意,要求饮料罐至少需要多少铁皮,实际上是求圆柱的表面积,根据公式圆柱的表面积=圆柱的侧面积+底面积×2,列式为:(5÷2)?×3.14×2+3.14×5×14= 259.05(平方厘米)≈260(平方厘米)
4.428平方厘米
解析:根据图意,要求笔筒至少需要多少平方厘米的材料,实际上是求圆柱的侧面积+一个底面积,侧面积是:25.12×15=376.8(平方厘米),底面半径是:25.12÷3.14÷2=4(厘米),表面积是:3.14×4?+376.8=50.24+376.8=427.04(平方厘米)≈428(平方厘米)
5.7.536平方米
解析:根据图意,要求压路的面积实际是求前轮的侧面积,根据圆柱的侧面积=底面周长×高,列式为:3.14×1.2×2=3.768×2=7.536(平方米)
拓展应用
1.答案:2
解析:因为圆柱的侧面积=底面周长×高,圆柱的底面半径扩大到原来的2倍,底面周长也扩大到原来的2倍,高不变,所以它的侧面积扩大到原来的2倍。
2.答案:36平方分米
解析:由锯木问题得:截成4段需要锯3次,每锯一次就增加2个截面的面积,锯3次一共增加6个截面的面积,列式为:6×6=36(平方分米)
3.答案:20096平方厘米
解析:此题就是求该圆柱的侧面积,利用公式列式为:3.14×20×40×8=20096(平方厘米)
4.答案:0.471千克。
解析:此题要先求出1根木桩的侧面积,再求5根同样的木桩的侧面积,最后根据“每平方米用油漆25克”,用每平方米用油漆的数量乘涂漆的面积即可,列式为:9.42分米=0.942米,0.942×4×5=3.768×5=18.84(平方米),25×18.84=471(克)=0.471(千克)
5.答案:3.14平方厘米。
解析:根据题干,切割后表面积减少了高为10厘米的圆柱的侧面积,由此利用减少的表面积62.8平方厘米,即可求出这个圆柱的底面半径,再利用圆的面积公式计算出圆柱的底面积。列式为:圆柱的底面半径是:62.8÷10÷3.14÷2=1(厘米).
所以圆柱的底面积是:3.14×1?=3.14(平方厘米)
信息窗3——圆柱体和圆锥体的体积计算
一、知识点解读
1. 圆柱体和圆锥体的体积计算(实际运用)
知识点: 推导圆柱体的体积计算,掌握计算方法。
教学要求:在长方体体积的计算基础上推导出圆柱体的计算。学习时借助圆柱体等分展开拼成方体得到圆柱体的体积计算。
知识点:圆锥体的体积计算
教学要求:在学会掌握圆柱体的体积计算时,推导圆锥体的体积计算。
知识点:圆柱和圆锥的关系
1. 圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2. 圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3. 圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4. 圆柱与圆锥等底等高 ,体积相差2∕3sh
教学要求:
在理解圆柱和圆锥的关系上解决相关的问题。
二、知识拓展
圆柱体和圆锥体的体积计算及应用。
三、知识点训练
基础训练
1. 圆柱的高有( )条,圆锥的高有( )条。
2. 一个圆锥的底面积是40cm2,高12㎝,体积是( )。
3. 一个圆柱的底面半径是3dm2,高2dm,它的侧面积是()dm2,表面积是( )dm2,体积是( )dm3。
4. 一个圆柱的底面周长6.28cm,高是3cm,它的体积是( )cm3。
5. 把一个底面直径是2分米,高是3分米的圆柱体削成一个最大的圆锥体,圆锥的体积是( )立方分米。
能力提升
1.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是15立方分米,圆柱的体积是( )立方分米。
A. 45 B. 15 C. 5
2.圆柱的底面半径扩大3倍,高不变,它的体积应扩大( )倍。
A. 3 B. 6 C. 9 D. 27
3.等底等高的圆柱. 正方体. 长方体的体积相比较( )。
A. 正方体体积大 B. 长方体体积大
C. 圆柱体体积大 D. 体积一样大
4.一个圆柱体杯中盛满15升水,把一个与它等底等高的铁圆锥倒放入水中,杯中还有( )水。
A. 5升 B. 7.5升 C. 10升 D. 9升
5.求圆柱形木桶内盛多少升水,就是求水桶的( )。
A. 侧面积 B. 表面积 C. 体积 D. 容积
拓展应用
1. 在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
2. 一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径6米,池深1.2米。镶瓷砖的面积是多少平方米?
3. 张师傅要把一根圆柱形木料(如下图)削成一个圆锥。
⑴这根木料的表面积是多少平方分米?
(2)削成的圆锥的体积最大是多少立方分米?
4. 一个装满玉米的圆柱形粮囤,底面周长6.28米,高2米。如果将这些玉米堆成一个高1米的圆锥形的玉米堆,圆锥底面积是多少平方米?
5. 欣欣把一块底面半径2厘米. 高6厘米的圆柱形橡皮泥捏成一个底面与圆柱底面相等的圆锥。圆锥的高是多少厘米?
综合与实践——立体的截面
一、知识点解读
1.截面的定义(理解识记)
知识点:用一个平面去截一个几何体,截出的面叫做截面。
教学要求:通过动脑猜想. 动手操作,实验验证等活动,初步体验截面的含义。
2.从不同的角度去截一个几何体,所得到的截面就有可能不同。(动手实践. 探究规律)
知识点:沿着物体不同的位置切下去,截面的形状不一定相同。
教学要求:综合运用学过的有关知识,探索沿着物体不同的位置切出的截面形状的变化规律
二、知识拓展
常见柱体的截面
三、知识点训练
基础训练
1. 沿着篮球的不同位置切开后的截面是( )形的。
2. 横着切和竖着切开鸡蛋后的截面分别是( )形的和( )形的。
3. 下面所给图形的截面正确的一项是( )。
能力提升
指出下面几何体的截面的形状( )。
2.用一个平面去截一个几何体如果截面的形状是圆,你能想象出原来的几何体是什么?
3. 用一个平面去截下列各几何体,所得截面与其它三个不同的是( )。
拓展应用
1. 用平面去截一个立体图形,如果截面是三角形,你能想象出原来的立体图形可能是什么吗?
2. 用平面分别截这些几何体,请你将截面的形状按对应的图号填表。
图形编号 (1) (2) (3) (4) (5) (6) (7) (8)
截面形状
训练题参考答案及解析
基础训练
1. 圆 2. 圆;椭圆 3. B
能力提升
D 2. 圆; 圆柱; 圆锥 3. D
拓展应用
立方体. 圆锥. 三角锥. 三棱柱
圆;三角形;圆;长方形(或正方形);三角形;梯形;三角形;长方形
85
信息窗2——圆柱的侧面积和表面积
一、知识点解读
1. 圆柱的侧面积计算公式(掌握运用)
知识点:圆柱的侧面积计算公式:圆柱的侧面积=底面周长×高,用字母表示为:S侧=Ch。
教学要求: 该知识点是学习圆柱侧面积计算公式的推导,是在掌握了长方形面积和圆的周长的的基础上推导出来的。学习时,可联系以前学过的平面图形面积公式的推导方法,把一个圆柱沿着高剪开,展开后是个长方形,长方形的长等于圆柱底面的周长,长方形的宽就是圆柱的高,由长方形的面积计算公式推导出圆柱侧面积计算公式。
2.圆柱的表面积的计算公式(掌握运用)
知识点:圆柱的表面积的计算公式:圆柱的侧面积+底面积×2,用字母表示为:S表=S侧+2S底。
教学要求:该知识点是认识圆柱的表面积以及学习圆柱的表面积计算方法,是在掌握圆柱的侧面积和圆的面积计算方法的基础上学习的。学习时,可在操作的过程中理解圆柱表面积的意义,并感悟圆柱表面积的计算方法。
二、知识拓展
求圆柱的表面积要具体情况具体分析,求用料多少,一般采用“进一法”取近似值,以保证原材料够用。
三、知识点训练
基础训练
1.
圆柱的侧面展开后是一个________,这个长方形的长等于圆柱的________,长方形的宽等于圆柱的________。因此圆柱的侧面积= ________________。
2. 圆柱的( )面积加上( )的面积,就是圆柱的表面积。
3. 求易拉罐上商标纸的面积,实际上是求( )。
4. 做一个油桶所需铁皮面积,实际上是求( )。
5. 圆柱的底面周长是2.1米,高0.9米。这个圆柱的侧面积是( )平方米。
能力提升
1. 一个圆柱底面直径是6dm,高是3dm,求它的表面积。
2. 一个圆柱,它的高是8厘米,侧面积是200.96平方厘米,它的底面积是( )。
3. 制作一个高14厘米,底面直径是5厘米的饮料罐,至少需要多少铁皮?(得数保留整数 )
4. 制作一个底面周长是25.12厘米的笔筒,大约需要多少平方厘米的材料?(得数保留整数 )
5. 一台压路机的前轮是圆柱形,轮宽2米,直径为1.2米,前轮滚动一周,压过的路是多少平方米?
拓展应用
1. 圆柱的底面半径扩大到原来的2倍,高不变,它的侧面积扩大到原来的( )倍。
2. 一根圆柱形木料,底面积是6平方分米,把它截成4段,表面积增加多少平方分米?
3. 用铁皮做8节同样大小的圆柱形通风管,每节的直径是20厘米,长40厘米,一共需要多少平方厘米的铁皮?
4.学校走廊有5根相同的圆形木桩,底面周长是9.42分米,高是4米,给这些木桩涂油漆,如果每平方米用油漆25克,一个需要多少千克油漆?
5. 一根圆柱形的木料,截去10厘米长的一小段后,剩下圆柱形木料的表面积比原来减少了62.8平方厘米。这根木料的底面积是多少平方厘米?
训练题参考答案及解析
基础训练
1. 长方形 底面周长 高 底面周长×高
2. 侧 2个底面
3. 圆柱的侧面积
4. 圆柱的表面积
5. 1.89
能力提升
1.113.04平方分米。
解析:因为圆柱的表面积=圆柱的侧面积+底面积×2,所以先求出底面的半径,再根据公式列式计算即可。
答案为6÷2=3(分米),3.14×6×3+3.14×3?×2=18.84×3+28.26×2=56.52+56.52=113.04(平方分米)
2.50.24平方厘米
解析:要求它的底面积,需要求出圆柱的底面半径,根据圆柱的侧面积=2πrh,可得r=侧面积÷(2πh),列式为:200.96÷(3.14×2×8)=200.96÷50.24=4(厘米),3.14×4?=3.14×16=50.24(平方厘米)
3.260平方厘米。
解析:根据图意,要求饮料罐至少需要多少铁皮,实际上是求圆柱的表面积,根据公式圆柱的表面积=圆柱的侧面积+底面积×2,列式为:(5÷2)?×3.14×2+3.14×5×14= 259.05(平方厘米)≈260(平方厘米)
4.428平方厘米
解析:根据图意,要求笔筒至少需要多少平方厘米的材料,实际上是求圆柱的侧面积+一个底面积,侧面积是:25.12×15=376.8(平方厘米),底面半径是:25.12÷3.14÷2=4(厘米),表面积是:3.14×4?+376.8=50.24+376.8=427.04(平方厘米)≈428(平方厘米)
5.7.536平方米
解析:根据图意,要求压路的面积实际是求前轮的侧面积,根据圆柱的侧面积=底面周长×高,列式为:3.14×1.2×2=3.768×2=7.536(平方米)
拓展应用
1.答案:2
解析:因为圆柱的侧面积=底面周长×高,圆柱的底面半径扩大到原来的2倍,底面周长也扩大到原来的2倍,高不变,所以它的侧面积扩大到原来的2倍。
2.答案:36平方分米
解析:由锯木问题得:截成4段需要锯3次,每锯一次就增加2个截面的面积,锯3次一共增加6个截面的面积,列式为:6×6=36(平方分米)
3.答案:20096平方厘米
解析:此题就是求该圆柱的侧面积,利用公式列式为:3.14×20×40×8=20096(平方厘米)
4.答案:0.471千克。
解析:此题要先求出1根木桩的侧面积,再求5根同样的木桩的侧面积,最后根据“每平方米用油漆25克”,用每平方米用油漆的数量乘涂漆的面积即可,列式为:9.42分米=0.942米,0.942×4×5=3.768×5=18.84(平方米),25×18.84=471(克)=0.471(千克)
5.答案:3.14平方厘米。
解析:根据题干,切割后表面积减少了高为10厘米的圆柱的侧面积,由此利用减少的表面积62.8平方厘米,即可求出这个圆柱的底面半径,再利用圆的面积公式计算出圆柱的底面积。列式为:圆柱的底面半径是:62.8÷10÷3.14÷2=1(厘米).
所以圆柱的底面积是:3.14×1?=3.14(平方厘米)
信息窗3——圆柱体和圆锥体的体积计算
一、知识点解读
1. 圆柱体和圆锥体的体积计算(实际运用)
知识点: 推导圆柱体的体积计算,掌握计算方法。
教学要求:在长方体体积的计算基础上推导出圆柱体的计算。学习时借助圆柱体等分展开拼成方体得到圆柱体的体积计算。
知识点:圆锥体的体积计算
教学要求:在学会掌握圆柱体的体积计算时,推导圆锥体的体积计算。
知识点:圆柱和圆锥的关系
1. 圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2. 圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3. 圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4. 圆柱与圆锥等底等高 ,体积相差2∕3sh
教学要求:
在理解圆柱和圆锥的关系上解决相关的问题。
二、知识拓展
圆柱体和圆锥体的体积计算及应用。
三、知识点训练
基础训练
1. 圆柱的高有( )条,圆锥的高有( )条。
2. 一个圆锥的底面积是40cm2,高12㎝,体积是( )。
3. 一个圆柱的底面半径是3dm2,高2dm,它的侧面积是()dm2,表面积是( )dm2,体积是( )dm3。
4. 一个圆柱的底面周长6.28cm,高是3cm,它的体积是( )cm3。
5. 把一个底面直径是2分米,高是3分米的圆柱体削成一个最大的圆锥体,圆锥的体积是( )立方分米。
能力提升
1.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是15立方分米,圆柱的体积是( )立方分米。
A. 45 B. 15 C. 5
2.圆柱的底面半径扩大3倍,高不变,它的体积应扩大( )倍。
A. 3 B. 6 C. 9 D. 27
3.等底等高的圆柱. 正方体. 长方体的体积相比较( )。
A. 正方体体积大 B. 长方体体积大
C. 圆柱体体积大 D. 体积一样大
4.一个圆柱体杯中盛满15升水,把一个与它等底等高的铁圆锥倒放入水中,杯中还有( )水。
A. 5升 B. 7.5升 C. 10升 D. 9升
5.求圆柱形木桶内盛多少升水,就是求水桶的( )。
A. 侧面积 B. 表面积 C. 体积 D. 容积
拓展应用
1. 在建筑工地上有一个近似于圆锥形状的沙堆,测得底面直径4米,高1.5米。每立方米沙大约重1.7吨,这堆沙约重多少吨?(得数保留整吨数)
2. 一个圆柱形水池,水池内壁和底面都要镶上瓷砖,水池底面直径6米,池深1.2米。镶瓷砖的面积是多少平方米?
3. 张师傅要把一根圆柱形木料(如下图)削成一个圆锥。
⑴这根木料的表面积是多少平方分米?
(2)削成的圆锥的体积最大是多少立方分米?
4. 一个装满玉米的圆柱形粮囤,底面周长6.28米,高2米。如果将这些玉米堆成一个高1米的圆锥形的玉米堆,圆锥底面积是多少平方米?
5. 欣欣把一块底面半径2厘米. 高6厘米的圆柱形橡皮泥捏成一个底面与圆柱底面相等的圆锥。圆锥的高是多少厘米?
综合与实践——立体的截面
一、知识点解读
1.截面的定义(理解识记)
知识点:用一个平面去截一个几何体,截出的面叫做截面。
教学要求:通过动脑猜想. 动手操作,实验验证等活动,初步体验截面的含义。
2.从不同的角度去截一个几何体,所得到的截面就有可能不同。(动手实践. 探究规律)
知识点:沿着物体不同的位置切下去,截面的形状不一定相同。
教学要求:综合运用学过的有关知识,探索沿着物体不同的位置切出的截面形状的变化规律
二、知识拓展
常见柱体的截面
三、知识点训练
基础训练
1. 沿着篮球的不同位置切开后的截面是( )形的。
2. 横着切和竖着切开鸡蛋后的截面分别是( )形的和( )形的。
3. 下面所给图形的截面正确的一项是( )。
能力提升
指出下面几何体的截面的形状( )。
2.用一个平面去截一个几何体如果截面的形状是圆,你能想象出原来的几何体是什么?
3. 用一个平面去截下列各几何体,所得截面与其它三个不同的是( )。
拓展应用
1. 用平面去截一个立体图形,如果截面是三角形,你能想象出原来的立体图形可能是什么吗?
2. 用平面分别截这些几何体,请你将截面的形状按对应的图号填表。
图形编号 (1) (2) (3) (4) (5) (6) (7) (8)
截面形状
训练题参考答案及解析
基础训练
1. 圆 2. 圆;椭圆 3. B
能力提升
D 2. 圆; 圆柱; 圆锥 3. D
拓展应用
立方体. 圆锥. 三角锥. 三棱柱
圆;三角形;圆;长方形(或正方形);三角形;梯形;三角形;长方形
85
