北京课改版九年级数学上册第19章 二次函数和反比例函数 综合测试卷 (含答案)
文档属性
| 名称 | 北京课改版九年级数学上册第19章 二次函数和反比例函数 综合测试卷 (含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 10:27:25 | ||
图片预览




文档简介
北京版九年级数学上册
第19章 二次函数和反比例函数
综合测试卷
(时间90分钟,满分120分)
一、选择题(共10小题,3*10=30)
1. 抛物线y=-2x2+1的对称轴是( )
A.直线x= B.直线x=-
C.y轴 D.直线x=2
2.若反比例函数y=的图象经过点(2,-1),则该反比例函数的图象在( )
A.第一、二象限 B.第一、三象限
C.第二、三象限 D.第二、四象限
3.将抛物线y=-2x2+1向右平移1个单位长度,再向上平移2个单位长度后所得到的抛物线为( )
A.y=-2(x+1)2-1 B.y=-2(x+1)2+3
C.y=-2(x-1)2+1 D.y=-2(x-1)2+3
4.在平面直角坐标系中,二次函数y=a(x-h)2(a≠0)的图象可能是( )
5.如图,点A是反比例函数y=(x>0)的图象上一点,过点A作AB⊥x轴于点B,连接OA,则△ABO的面积为( )
A.12 B.6
C.2 D.3
6.已知二次函数y=x2-2mx-3,下列结论不一定成立的是( )
A.它的图象与x轴有两个交点
B.方程x2-2mx=3的两根之积为-3
C.它的图象的对称轴在y轴的右侧
D.当x<m时,y随x的增大而减小
7.如图所示的桥拱是抛物线形,其函数的表达式为y=-x2,当水位线在AB位置时,水面宽12 m,这时水面离桥顶的高度为( )
8.二次函数y=ax2+bx+c的图象如图所示,则反比例函数y=与正比例函数y=bx在同一坐标系内的大致图象是( )
9. 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是( )
A.1个 B.2个
C.3个 D.4个
10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b
A.5个 B.4个
C.3个 D.2个
二.填空题(共8小题,3*8=24)
11.二次函数y=x2-6x+21的图象的开口向________,顶点坐标为________.
12.若点A(a,b)在反比例函数y=的图象上,则代数式ab-4的值为________.
13. 已知函数y=ax2+bx+c,当x=3时,函数取最大值4,当x=0时,y=-14,则函数表达式为________________________.
14.如图,菱形ABCD的面积为6,边AD在x轴上,边BC的中点E在y轴上,反比例函数y=的图象经过顶点B,则k的值为_______.
15.如图,已知反比例函数y=-的图象与正比例函数y=-x的图象交于A,B两点,若点A的坐标为(-2,),则点B的坐标为____________.
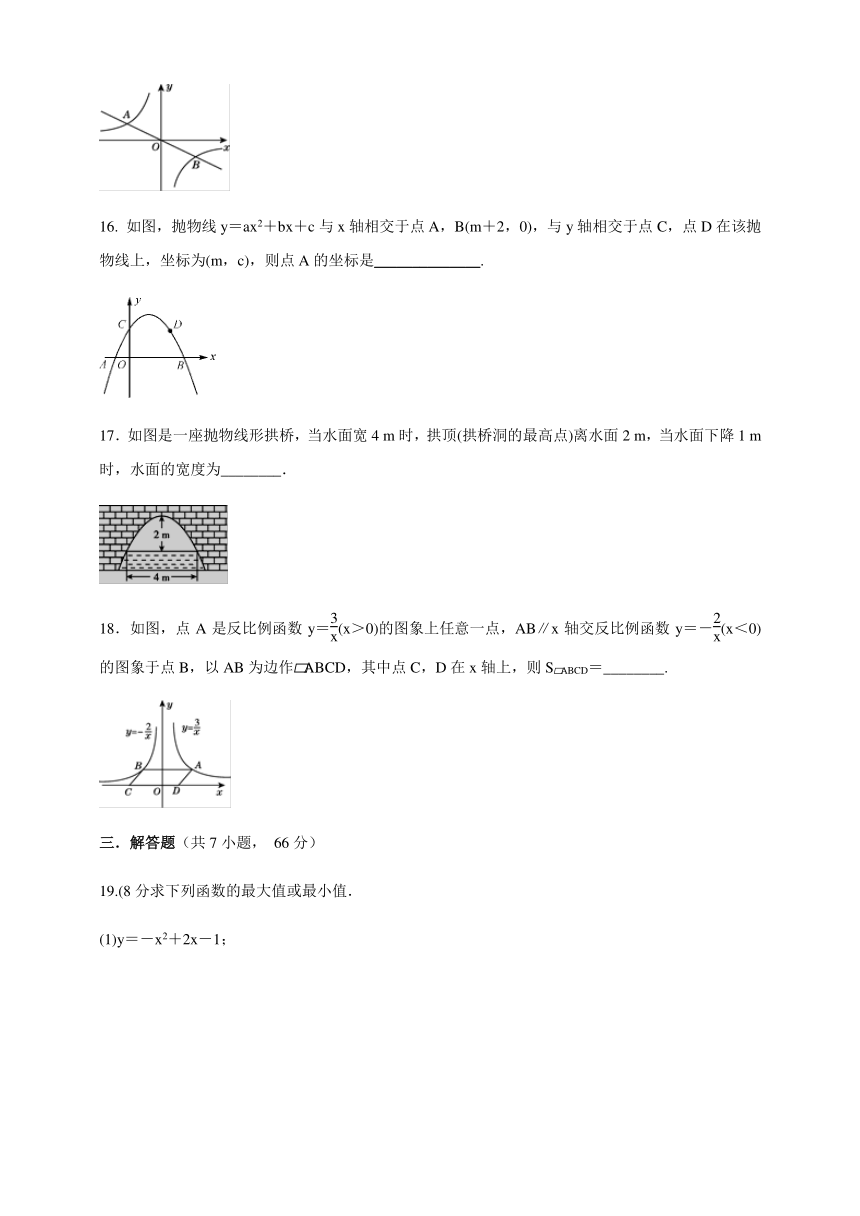
16. 如图,抛物线y=ax2+bx+c与x轴相交于点A,B(m+2,0),与y轴相交于点C,点D在该抛物线上,坐标为(m,c),则点A的坐标是______________.
17.如图是一座抛物线形拱桥,当水面宽4 m时,拱顶(拱桥洞的最高点)离水面2 m,当水面下降1 m时,水面的宽度为________.
18.如图,点A是反比例函数y=(x>0)的图象上任意一点,AB∥x轴交反比例函数y=-(x<0)的图象于点B,以AB为边作?ABCD,其中点C,D在x轴上,则S?ABCD=________.
三.解答题(共7小题, 66分)
19.(8分求下列函数的最大值或最小值.
(1)y=-x2+2x-1;
(2)y=4x2-4x-6.
20.(8分)如图,在平面直角坐标系xOy中,双曲线y=与直线y=-2x+2交于点A(-1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=-2x+2另一个交点B的坐标.
21.(8分) 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=(m≠0,x<0)的图象交于点A(-3,1)和点C,与y轴交于点B,△AOB的面积是6.
(1)求一次函数与反比例函数的表达式;
(2)当x<0时,比较y1与y2的大小.
22.(10分)某产品每件的成本是120元,试销阶段,每件产品的销售价x(元)与产品的日销售量y(件)的关系如下表:
x/元 130 150 165
y/件 70 50 35
(1)若日销售量y(件)是每件产品的销售价x(元)的一次函数,求y与x的函数关系式.
(2)若每日获得的利润用P(元)表示,求P与x之间的函数关系式.
(3)当每件产品的销售价为多少元时,才能使每日获得最大利润?最大利润为多少?
23.(10分)如图,某足球运动员站在点O处练习射门,将足球从离地面0.5 m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8 s时,离地面的高度为3.5 m.
(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?
(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10 t,已知球门的高度为2.44 m,如果该运动员正对球门射门时,离球门的水平距离为28 m,他能否将球直接射入球门?
24.(10分) 如图所示,有一条双向公路隧道,其截面由抛物线和矩形ABCO组成,隧道最大高度为4.9 m,AB=10 m,BC=2.4 m.现把隧道的截面放在直角坐标系中,若有一辆高为4 m、宽为2 m的装有集装箱的汽车要通过隧道,如果不考虑其他因素,汽车的右侧离隧道的右壁超过多少米才不至于碰到隧道顶部?(抛物线部分为隧道顶部,AO,BC为壁)
25.(12分) 如图,已知一次函数y=x-3的图象与反比例函数y=的图象相交于点A(4,n),与x轴相交于点B.
(1)n的值为__________,k的值为__________;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
参考答案
1-5 CDDDD 6-10 CDCCC
11.上;(6,3)
12.0
13. y=-2(x-3)2+4
14. 3
15.(2,-)
16. (-2,0)
17. 2 m
18.5
19.解:(1)∵y=-x2+2x-1=-(x2-2x+1)=-(x-1)2.
∴函数有最大值,最大值是0.
(2)∵y=4x2-4x-6
=4(x2-x+)-7
=4(x-)2-7.
∴函数有最小值,最小值是-7.
20. 解:(1)∵点A的坐标是(-1,a),点A在直线y=-2x+2上,
∴a=-2×(-1)+2=4.
∴点A的坐标是(-1,4),代入y=,
得m=-4.
(2)解方程组
得或
∴该双曲线与直线y=-2x+2另一个交点B的坐标为(2,-2).
21. 解:(1)y1=x+4,y2=-
(2)联立方程组
解得
∴点C的坐标为(-1,3),
∴当-1<x<0或x<-3时,y1<y2,
当-3<x<-1时,y1>y2,
当x=-1或x=-3时,y1=y2
22.解:(1)设y与x之间的函数关系式为y=kx+b,
将(130,70),(150,50)代入得
解得
∴y与x的函数关系式为y=-x+200.
(2)P=(x-120)y
=(x-120)(-x+200)
=-x2+320x-24 000(120≤x≤200).
(3)∵P=-x2+320x-24 000
=-(x-160)2+1 600,
∴当每件产品的销售价为160元时,才能使每日获得最大利润,最大利润为1 600元.
23. 解:(1)将(0,0.5)和(0.8,3.5)代入y=at2+5t+c,
得a=-,c=0.5,∴y=-t2+5t+0.5=-(t-)22+4.5.
∴足球飞行的时间是1.6s时,足球离地面最高,最大高度是4.5m
(2)当x=28时,28=10t,∴t=2.8.
当t=2.8时,y=-×+5×2.8+0.5=2.25(m).
∵0<2.25<2.44,∴他能将球直接射入球门
24.解:如图所示,由题意得抛物线的顶点坐标为(5,2.5),且过点O(0,0)和点C(10,0),可求出抛物线的函数表达式为y=-x2+x.用矩形DEFG表示汽车的截面,设BD=m,直线DG交抛物线于H,交x轴于M,则AD=
10-m,HM=-(10-m)2+10-m.
∴HD=-(10-m)2+10-m+2.4.
由题意得-(10-m)2+12.4-m>4,
化简得(m-2)(m-8)<0,∴2<m<8.
故汽车的右侧离隧道右壁超过2 m才不至于碰到隧道顶部.
25.解:(1)3;12
(2)直线y=x-3与x轴相交于点B,
令x-3=0,得x=2.
∴B点坐标为(2,0).
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F.
∵A(4,3), B(2,0),
∴OE=4,AE=3,OB=2.
∴BE=OE-OB=4-2=2.
在Rt△ABE中,AB===.
∵四边形ABCD是菱形,
∴AB=CD=BC=,AB∥CD.
∴∠ABE=∠DCF.
又∵AE⊥x轴, DF⊥x轴,
∴∠AEB=∠DFC=90°.
∴△ABE≌△DCF(AAS).
∴CF=BE=2,DF=AE=3.
∴OF=OB+BC+CF=2++2=4+.
∴点D的坐标为(4+,3).
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
