六年级下册数学说课课件- 3.2.2 圆锥的体积 人教版(共45张PPT)
文档属性
| 名称 | 六年级下册数学说课课件- 3.2.2 圆锥的体积 人教版(共45张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 14:06:57 | ||
图片预览






文档简介
(共45张PPT)
人教版小学数学六年级下册第三单元
<<圆锥的体积>>说课
设计理念
教材分析
教法学法
说课内容
说
教学过程
教学
反思
教学目标
一、教材分析:说教材的地位和作用
圆锥是小学几何初步知识的最后一个教学内容,是学生在学习了平面图形以及长方体、正方体、圆柱体这三种立体图形的基础上进行研究的。以进一步发展学生的空间观念,为学生学习其它图形知识打下坚实的基础为目标。
学 情 分 析
五年级
长、正方体的体积
六年级圆柱
的体积
生活经验
一年级
认识物体
基 础
学 生
六年级学生已有了一定的生活经验,对空间观念也有了一定的了解。从一年级开始就认识了物体,五年级学习了长方体、正方体的体积,在前面刚学了圆柱的体积,在此基础上学习圆锥的体积,学生很容易掌握,做到水到渠成。
学 情 分 析
二.说设计理念
1.选择学生身边感兴趣的事物作为素材,激发学生的好奇心。
2.强化情景创设功能增强学生探索的欲望。
3.创建良好的动手实验操作的探究环境,让学生在快乐的气氛下实验探索新知。
三、说教学目标:
(1)通过实验,理解并掌握圆锥体积公式的推导过程,学会运用计算公式,并能解决一些实际问题。
(2)通过圆锥体积公式的推导实验,培养学生的观察思维能力和动手操作能力。
(3)引导学生探索知识的内在联系,渗透转化思想,培养合作交流的团队精神。
教学重点:运用圆锥的体积公式。
教学难点:理解圆锥体积公式的推导过程。
教具准备:一对等底等高的空心圆柱、圆锥容器、水(沙)、学生实验所用等底等高的空心圆柱、圆锥容器若干(学生自制的圆柱及各类型的圆锥若干)三角尺、直尺等.
四、说教法与学法:
1.教法:根据学生的认知规律、实际水平,以及教学内容的特点,采用情境教学法、实验操作法、 比较讨论法,通过实验推导圆锥的体积公式。
2.学法:采用分组自主合作探究式的学习模式,通过猜想讨论、实践操作,验证归纳等学习活动,使学生从形象思维逐步过渡到抽象思维,进而达到感知验证新知、应用新知、巩固和深化新知的目的。
“操作实验”课堂教学
教 学 模 式
育人为本
基本知识
基本技能
道德修养
社会责任感
课堂模式
“操作实验”课堂教学
完成课堂教学
提
出
问
题
探
索
实
验
合
作
交
流
推
理
归
纳
解
决
问
题
达
标
训
练
反
思
提
升
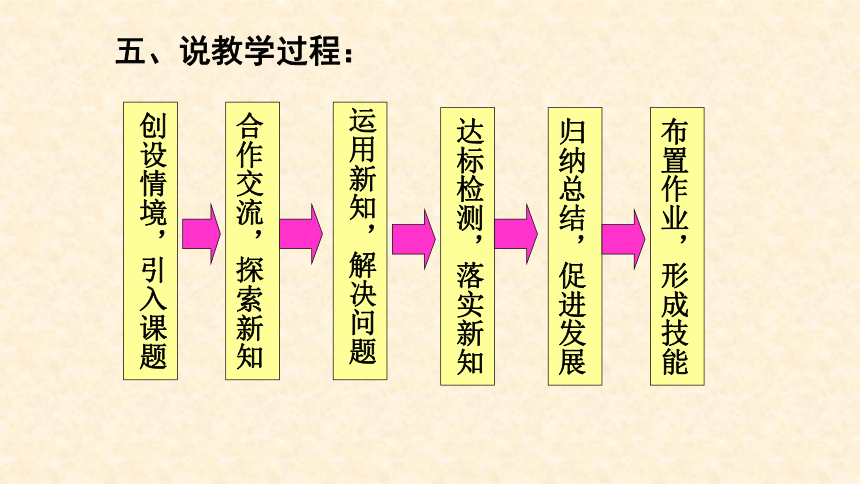
创设情境,引入课题
合作交流,探索新知
布置作业,形成技能
运用新知,解决问题
归纳总结,促进发展
达标检测,落实新知
五、说教学过程:
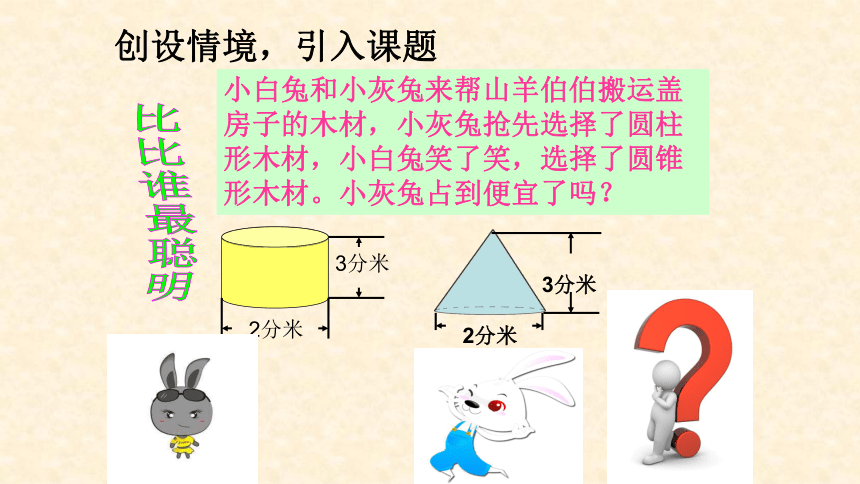
小白兔和小灰兔来帮山羊伯伯搬运盖房子的木材,小灰兔抢先选择了圆柱形木材,小白兔笑了笑,选择了圆锥形木材。小灰兔占到便宜了吗?
2分米
3分米
2分米
3分米
比比谁最聪明
创设情境,引入课题
圆锥的体积怎么求呢?
创设情境,引入课题
合作交流,探索新知
一、合理猜想,指引方向
选择哪种立体图形研究圆锥的体积更合适?为什么?
我们用实验法来探索圆锥体积的计算方法。
二:教师指导,探索实验
1、学生分组,准备学具。
2、出示实验要求:
量一量,圆柱和圆锥的底和高之间有什么关系?
空心圆锥装满沙或水倒进空心圆柱中,几次可以将空圆柱装满?
3、学生分组实验。
合作交流,探索新知
4、通过实验总结等底等高的圆柱和圆锥的关系。
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
三:全班交流,汇报结果 ,
合作交流,探索新知
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
V= sh
圆柱体积=底面积 高
圆锥体积=
V= sh
圆柱体积=底面积 高
圆锥体积=
底面积 高
V= sh
圆柱体积=底面积 高
圆锥体积=
学习任何知识的最佳道路是由自己去发现,因为这种发现更深刻,也最容易把握其中的内在规律,通过上面这个实验,可以让学生了解圆锥体积公式的推导过程,也有助于培养学生的观察思维能力和动手操作能力。
运用新知,解决问题
1.判断对错。
(1)圆锥的体积等于圆柱体积的三分之一。( )
(2)圆柱体积大于与它等底等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。( )
圆柱的体积:
3.14×(2÷2)2×3
=9.42(立方分米)
圆锥的体积:
×3.14×(2÷2)2×3
=3.14(立方分米)
2分米
3分米
2分米
3分米
运用新知,解决问题
2、回归情境
打谷场上,有一个近似圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重735千克,这堆小麦大约有多少千克?
1.2米
4米
运用新知,解决问题
3、解决实际问题
达标检测,落实新知
1、填一填,求出相应的圆锥的体积。
(1)底面积30平方厘米,高5厘米,体积是( )。
(2)底面半径4分米,高是3分米,体积是( )。
(3)底面周长31.4厘米,高6厘米,体积是( )。
比比谁知道得多
达标检测,落实新知
2、
3、把一个棱长是6厘米的正方体木块,加工成一个最大圆锥体,这个圆锥体的体积是多少?
达标检测,落实新知
全课总结,促进发展
1、上了这节课,你有什么收获?
2、用什么方法获取的?你认为哪组表现最棒?
3、通过这节课的学习,你有什么新的想法?还有什么问题?
推荐作业
1、必做题:这个陀螺的体积是多少?(单位:分米)
2、选做题:在课外选一个实物圆锥体,自己测量,算出它的体积。
3
3
6
圆锥的体积:等于和它等底等高 的圆柱体积的1/3。
圆锥体积=底面积×高× 1/3
用字母表示 V=1/3Sh
基础练习
达标练习
板书设计
1、创设情境,引起兴趣 2分钟
2、实验操作,自主探究 16分钟
3、运用新知,解决问题 10分钟
4、达标检测,落实新知 10分钟
5、归纳总结,作业布置 2分钟
时间分配:
用好教材资源
活用生活资源
巧用学生资源
圆锥的体积
资源开发
资源开发
多媒体资源
1.通过实验,得到等底等高的圆柱和圆锥体积之间的关系,推导出圆锥的体积计算公式。
2.在推导过程中,带着思考题进行实验,更有目的性、操作性。
3.练习题由浅入深,考察学生的解决实际问题的能力及策略。
4.时间分配上不到位,在例题的处理上,由于最终结果计算量较大,考虑到本节课的重点是理解公式并运用公式,没有留出充分的时间让每一位学生算出最终答案。
5.实验误差。
六、说教学反思
人教版小学数学六年级下册第三单元
<<圆锥的体积>>说课
设计理念
教材分析
教法学法
说课内容
说
教学过程
教学
反思
教学目标
一、教材分析:说教材的地位和作用
圆锥是小学几何初步知识的最后一个教学内容,是学生在学习了平面图形以及长方体、正方体、圆柱体这三种立体图形的基础上进行研究的。以进一步发展学生的空间观念,为学生学习其它图形知识打下坚实的基础为目标。
学 情 分 析
五年级
长、正方体的体积
六年级圆柱
的体积
生活经验
一年级
认识物体
基 础
学 生
六年级学生已有了一定的生活经验,对空间观念也有了一定的了解。从一年级开始就认识了物体,五年级学习了长方体、正方体的体积,在前面刚学了圆柱的体积,在此基础上学习圆锥的体积,学生很容易掌握,做到水到渠成。
学 情 分 析
二.说设计理念
1.选择学生身边感兴趣的事物作为素材,激发学生的好奇心。
2.强化情景创设功能增强学生探索的欲望。
3.创建良好的动手实验操作的探究环境,让学生在快乐的气氛下实验探索新知。
三、说教学目标:
(1)通过实验,理解并掌握圆锥体积公式的推导过程,学会运用计算公式,并能解决一些实际问题。
(2)通过圆锥体积公式的推导实验,培养学生的观察思维能力和动手操作能力。
(3)引导学生探索知识的内在联系,渗透转化思想,培养合作交流的团队精神。
教学重点:运用圆锥的体积公式。
教学难点:理解圆锥体积公式的推导过程。
教具准备:一对等底等高的空心圆柱、圆锥容器、水(沙)、学生实验所用等底等高的空心圆柱、圆锥容器若干(学生自制的圆柱及各类型的圆锥若干)三角尺、直尺等.
四、说教法与学法:
1.教法:根据学生的认知规律、实际水平,以及教学内容的特点,采用情境教学法、实验操作法、 比较讨论法,通过实验推导圆锥的体积公式。
2.学法:采用分组自主合作探究式的学习模式,通过猜想讨论、实践操作,验证归纳等学习活动,使学生从形象思维逐步过渡到抽象思维,进而达到感知验证新知、应用新知、巩固和深化新知的目的。
“操作实验”课堂教学
教 学 模 式
育人为本
基本知识
基本技能
道德修养
社会责任感
课堂模式
“操作实验”课堂教学
完成课堂教学
提
出
问
题
探
索
实
验
合
作
交
流
推
理
归
纳
解
决
问
题
达
标
训
练
反
思
提
升
创设情境,引入课题
合作交流,探索新知
布置作业,形成技能
运用新知,解决问题
归纳总结,促进发展
达标检测,落实新知
五、说教学过程:
小白兔和小灰兔来帮山羊伯伯搬运盖房子的木材,小灰兔抢先选择了圆柱形木材,小白兔笑了笑,选择了圆锥形木材。小灰兔占到便宜了吗?
2分米
3分米
2分米
3分米
比比谁最聪明
创设情境,引入课题
圆锥的体积怎么求呢?
创设情境,引入课题
合作交流,探索新知
一、合理猜想,指引方向
选择哪种立体图形研究圆锥的体积更合适?为什么?
我们用实验法来探索圆锥体积的计算方法。
二:教师指导,探索实验
1、学生分组,准备学具。
2、出示实验要求:
量一量,圆柱和圆锥的底和高之间有什么关系?
空心圆锥装满沙或水倒进空心圆柱中,几次可以将空圆柱装满?
3、学生分组实验。
合作交流,探索新知
4、通过实验总结等底等高的圆柱和圆锥的关系。
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
等底等高的:
再次强调:
三:全班交流,汇报结果 ,
合作交流,探索新知
圆柱体积=底面积 高
1
3
圆锥体积=
底面积 高
V= sh
圆柱体积=底面积 高
圆锥体积=
V= sh
圆柱体积=底面积 高
圆锥体积=
底面积 高
V= sh
圆柱体积=底面积 高
圆锥体积=
学习任何知识的最佳道路是由自己去发现,因为这种发现更深刻,也最容易把握其中的内在规律,通过上面这个实验,可以让学生了解圆锥体积公式的推导过程,也有助于培养学生的观察思维能力和动手操作能力。
运用新知,解决问题
1.判断对错。
(1)圆锥的体积等于圆柱体积的三分之一。( )
(2)圆柱体积大于与它等底等高的圆锥的体积。( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。( )
圆柱的体积:
3.14×(2÷2)2×3
=9.42(立方分米)
圆锥的体积:
×3.14×(2÷2)2×3
=3.14(立方分米)
2分米
3分米
2分米
3分米
运用新知,解决问题
2、回归情境
打谷场上,有一个近似圆锥的小麦堆,测得底面直径是4米,高是1.2米。每立方米小麦约重735千克,这堆小麦大约有多少千克?
1.2米
4米
运用新知,解决问题
3、解决实际问题
达标检测,落实新知
1、填一填,求出相应的圆锥的体积。
(1)底面积30平方厘米,高5厘米,体积是( )。
(2)底面半径4分米,高是3分米,体积是( )。
(3)底面周长31.4厘米,高6厘米,体积是( )。
比比谁知道得多
达标检测,落实新知
2、
3、把一个棱长是6厘米的正方体木块,加工成一个最大圆锥体,这个圆锥体的体积是多少?
达标检测,落实新知
全课总结,促进发展
1、上了这节课,你有什么收获?
2、用什么方法获取的?你认为哪组表现最棒?
3、通过这节课的学习,你有什么新的想法?还有什么问题?
推荐作业
1、必做题:这个陀螺的体积是多少?(单位:分米)
2、选做题:在课外选一个实物圆锥体,自己测量,算出它的体积。
3
3
6
圆锥的体积:等于和它等底等高 的圆柱体积的1/3。
圆锥体积=底面积×高× 1/3
用字母表示 V=1/3Sh
基础练习
达标练习
板书设计
1、创设情境,引起兴趣 2分钟
2、实验操作,自主探究 16分钟
3、运用新知,解决问题 10分钟
4、达标检测,落实新知 10分钟
5、归纳总结,作业布置 2分钟
时间分配:
用好教材资源
活用生活资源
巧用学生资源
圆锥的体积
资源开发
资源开发
多媒体资源
1.通过实验,得到等底等高的圆柱和圆锥体积之间的关系,推导出圆锥的体积计算公式。
2.在推导过程中,带着思考题进行实验,更有目的性、操作性。
3.练习题由浅入深,考察学生的解决实际问题的能力及策略。
4.时间分配上不到位,在例题的处理上,由于最终结果计算量较大,考虑到本节课的重点是理解公式并运用公式,没有留出充分的时间让每一位学生算出最终答案。
5.实验误差。
六、说教学反思
