六年级下册数学单元测试-2.位置 冀教版 (含解析)
文档属性
| 名称 | 六年级下册数学单元测试-2.位置 冀教版 (含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 224.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 14:18:38 | ||
图片预览




文档简介
六年级下册数学单元测试-2.位置
一、单选题
1.如图,如果点X的位置为(2,3),则点Y的位置为( ? ?? )。
A.?(4,4)????????????????????????B.?(4,5)????????????????????????C.?(5,4)????????????????????????D.?(3,3)
2.如图,如果点X的位置表示为(2,3),则点Y的位置可以表示为(??? )。
A.?(4,4)?????????????????????????????????B.?(4,5)?????????????????????????????????C.?(5,4)?????????????????????????????????D.?(3,3)
3.我们能用(??????? )表示一些物体的位置。
A.?方向?????????????????????????????????????????B.?距离?????????????????????????????????????????C.?数对
4.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,那么(10,20)表示的位置是(? )
A.?点A??????????????????????????????????????B.?点B??????????????????????????????????????C.?点C??????????????????????????????????????D.?点D
二、判断题
5.用(x,9)表示位置,不知道在第几行,但知道是第9列。
6.小小的位置在第5行,第8列,用对数表示为(5,8).(判断对错)
7.数对(3,4)和(5,4)表示的位置是在同一行.(判断对错)
8.判断,正确的填“正确”,错误的填“错误”. 把第2排第3个涂上颜色.★在第几排第几个? 答:★在第6排第4个.
三、填空题
9.在确定一个点的位置时,一般都把该点对应的横轴上的数写在________面,把纵轴上的数写在________面.
10.如图,方格纸的每个小方格的边长都是1的正方形,A,B两点在小方格的顶点上,A点的位置可以用(1,1)表示;B点的位置可用(2,3)表示.现在要在小方格的顶点上找到C点,连接AB,AC和BC后得三角形,且三角形ABC的面积为2.请你找出5个符合条件的C点,并在下面用数对表示出各点的位置. C1________,C2________,C3________,C4________,C5________.
11.右图中B点在(4,2),那么A点在________,以AB所在的直线为对称轴,C点的对称点C'的位置是________。
12.学校组织同学们去电影院看电影,聪聪坐在(6,4)的位置,明明坐在(6,2)的位置,亮亮和他们俩坐在同一条直线上,亮亮的位置可能是(________,________)
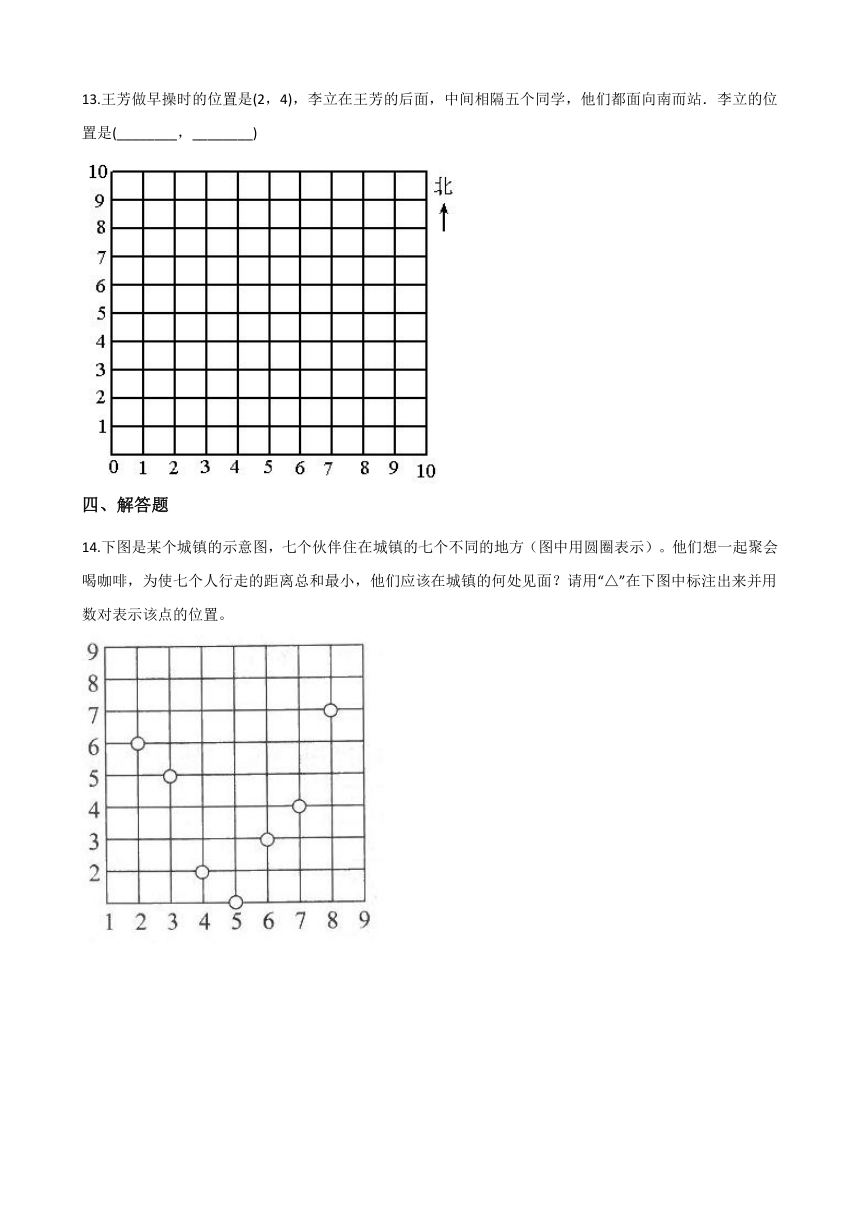
13.王芳做早操时的位置是(2,4),李立在王芳的后面,中间相隔五个同学,他们都面向南而站.李立的位置是(________,________)
四、解答题
14.下图是某个城镇的示意图,七个伙伴住在城镇的七个不同的地方(图中用圆圈表示)。他们想一起聚会喝咖啡,为使七个人行走的距离总和最小,他们应该在城镇的何处见面?请用“△”在下图中标注出来并用数对表示该点的位置。
15.下面是五一班学生座位平面图
(1)王兵坐在第2列第5行,请你在图中用“△”标出王兵的位置.用数对表示是________.
(2)钟卫的位置是(4,3),在图中是第________列第________行,在平面图中用“☆”标出钟卫的位置.
(3)在平面图中分别用A、B标出(6,4)和(4,6)的位置.
(6,4)和(4,6)表示的位置一样吗?为什么?
(4)赵洪的位置是(3,3).他前面的座位上是王丽,用数对表示是(3,2),后面的座位上是胡小平,左边的座位上是马兵,右边的座位上是李然.请用数对分别表示胡小平、马兵、李然的位置.
五、作图题
16.描出下面各点并连成封闭图形.A(5,9)B(1,6)C(5,6)
六、综合题
17.《汽车司机使用交通图册》中有这样一个“里程速查表”(如图,单位:千米).312国道从南京到上海的8个城市中,任意两个城市之间的公路里程都可以迅速地从该表中查到.比如,查镇江到无锡的公路里程,可以现在表中找到“镇江”,往下看,有一列数;再找到“无锡”,往左看一行数.这一列和一行数的交叉点处的数“122”,就是镇江到无锡的公路里程数.
(1)上海到南京的公路里程是________千米,如果乘坐的汽车行驶的平均速度是80千米/小时,从上海到南京需要________小时.
(2)按照图中的规律可以推算:A=________,B=________.
参考答案
一、单选题
1.【答案】C
【解析】【解答】如果点X的位置为(2,3),则点Y的位置为(5,4). 故答案为:C.
【分析】用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,据此可以得到点Y在第5列第4行,用数对表示为(5,4).
2.【答案】 C
【解析】【解答】解:Y在5列4行,用数对表示是(5,4)。 故答案为:C
【分析】数对中第一个数表示列,第二个数表示行。判断出Y所在的列与行用数对表示出来即可。
3.【答案】C
【解析】【解答】解:我们能用数对表示一些物体的位置。 故答案为:C。
【分析】方向和距离能描述两个物体的相对位置,数对能表示物体的位置,据此解答即可。
4.【答案】 B
【解析】【解答】解:根据如图所建的坐标系,易知(10,20)表示的位置是点B,
故选:B.
【分析】根据题意可得:小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,即向西走为x轴负方向,向南走为y轴负方向;则(10,20)表示的位置是向东10,北20;即点B所在位置.本题考查了学生利用类比点坐标解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置,或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
二、判断题
5.【答案】错误
【解析】【解答】用(x,9)表示位置,不知道在第几列,但知道是第9行,原题说法错误. 故答案为:错误. 【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行,据此判断.
6.【答案】错误
【解析】【解答】解:小小的位置在第5行,第8列,用对数表示为(8,5),不是(5,8), 原题说法错误. 故答案为:错误. 【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可确定小小的位置,再与(5,8)比较.
7.【答案】正确
【解析】【解答】解:(3,4)表示第3列第4行,(5,4)表示第5列第4行,它们都表示第4行; 原题说法正确. 故答案为:正确. 【分析】数对表示位置时,第一个数表示列数,第二个数表示行数;所以(3,4)表示第3列第4行,(5,4)表示第5列第4行,据此做出判断.
8.【答案】错误
【解析】【解答】 答:★在第4排第6个. 横为行,也就是排,第几行也就是第几排.第2排应该是第2横行,第3个应该是从左往右数第3个,而不应该是从上往下数第3个.因为第1问在涂颜色时横、竖没有分清楚,所以第2问的答案也不正确.
三、填空题
9.【答案】前;后
【解析】【解答】在确定一个点的位置时,一般都把该点对应的横轴上的数写在前面,把纵轴上的数写在后面. 故答案为:前;后 【分析】写在前面的数也就是数对中第一个数,表示所在的列,第二个数写在后面,表示所在的行.
10.【答案】(3,1);(0,3);(4,3);(5,5);(1,5)
【解析】【解答】解:如图所示: 用数对表示出各点的位置是: C1(3,1);C2(0,3);C3 (4,3);C4 (5,5);C5 (1,5). 故答案为:(3,1);(0,3);(4,3);(5,5);(1,5). 【分析】AB之间的水平距离为2,只要到点A或B等于2的在格点上的点都符合.AB之间的垂直距离为1,只要到点A或B等于4的在格点上的点都符合,再利用数对表示位置的方法即可标出各点的位置.三角形的面积等于底×高÷2,所以只需找到水平距离,或垂直距离,就能得到符合条件的另一点的位置.
11.【答案】(4,5);(3,1)
【解析】【解答】解:A点在4列5行,是(4,5);C′在3列1行,是(3,1). 故答案为:(4,5);(3,1) 【分析】数对中第一个数表示列,第二个数表示行,根据B点的位置确定列与行的计数方法后用数对表示A和C′的位置即可.
12.【答案】6;1
【解析】【解答】学校组织同学们去电影院看电影,聪聪坐在(6,4)的位置,明明坐在(6,2)的位置,亮亮和他们俩坐在同一条直线上,亮亮的位置可能是(6,1),(第2个空答案不唯一). 故答案为:6;1.
【分析】根据题意可知,聪聪、明明、亮亮在同一列,那么它们的列数相同,也就是数对中的第一个数字相同,行数不同,也就是第二个数字不同,据此解答.
13.【答案】2;10
【解析】【解答】如图: 李立的位置是(2,10) 故答案为:2;10 【分析】数对中第一个数表示列,第二个数表示行,后方是北方,确定出李立的位置后用数对表示李立的位置即可.
四、解答题
14.【答案】 解:七个人到竖向最近的位置是七个人的中间位置,在第5竖街区;七个人到横向最近的位置是七个人的中间位置,在第4横街区。故他们应在第5竖街区与第4横街区交会处见面,即(5,4)处。
【解析】【分析】要想七个人行走的距离总和最小,只需要找出行与列的中间位置即可;这些位置中,第一个数最小是2,最大是8,取中间是第5列,第二个数最小是0,最大是7,取中间是第4行,所以他们应在第5竖街区与第4横街区交会处见面,即(5,4)处。
15.【答案】(1)(2,5) (2)4;3 (3)解:位置不一样,(6,4)表示6列4行,(4,6)表示4列6行. (4)解:胡小平是(3,4),马兵是(4,3),李然是(2,3).
【解析】【解答】(1)2列5行用数对表示是(2,5); (2)(4,3)表示在4列3行; (3)根据所在的列与行判断两个位置是否一样; (4)从图中找出三人的位置,并用数对表示出来. 如图: 故答案为:(1)(2,5);(2)4;3;(3)位置不一样,(6,4)表示6列4行,(4,6)表示4列6行;(4)胡小平是(3,4),马兵是(4,3),李然是(2,3).
【分析】数对中第一个数表示列,第二个数表示行,按照这个规律判断出所在的列与行分别解答各个小题即可.
五、作图题
16.【答案】解:根据数对表示位置的方法在平面图中标出各点的位置,并顺次连接起来得出直角三角形ABC如下图所示:
【解析】【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行.由此即可标出图中各个点的位置.此题主要考查了数对的意义,即在数对中,第一个数表示第几列,第二个数表示第几行.
六、综合题
17.【答案】(1)352 ;4.4
(2)258 ;94
【解析】【解答】解:(1)由图可知,上海到南京的公路里程是352千米,
根据时间=路程÷速度,从上海到南京所需时间为:352÷80=4.4(小时),
(2)由题意可知:A=南京至无锡的里程数+无锡至苏州的里程数=197+61=258,
B=苏州至昆山的里程数+昆山至上海的里程数=40+54=94.
故答案为:(1)352,4.4;(2)258,94.
【分析】(1)根据题意可知,上海到南京的公路里程数就是上海所对应的一行数与南京所对应的一列数的交叉点处的数,由图可知答案,再根据路程、速度与时间之间的关系,已知路程和速度,求出时间即可;(2)由图可知A表示南京至苏州的公路里程数,B表示苏州至上海的公路里程数.图中的规律可以理解为:甲到丙的里程数=甲到乙的里程数+乙到丙的里程数,因而,A=南京至无锡的里程数+无锡至苏州的里程数,B=苏州至昆山的里程数+昆山至上海的里程数,由图找出相关数据,相加即可.本题考查了数对与位置,要善于根据题意,结合图形,寻找规律.
一、单选题
1.如图,如果点X的位置为(2,3),则点Y的位置为( ? ?? )。
A.?(4,4)????????????????????????B.?(4,5)????????????????????????C.?(5,4)????????????????????????D.?(3,3)
2.如图,如果点X的位置表示为(2,3),则点Y的位置可以表示为(??? )。
A.?(4,4)?????????????????????????????????B.?(4,5)?????????????????????????????????C.?(5,4)?????????????????????????????????D.?(3,3)
3.我们能用(??????? )表示一些物体的位置。
A.?方向?????????????????????????????????????????B.?距离?????????????????????????????????????????C.?数对
4.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,那么(10,20)表示的位置是(? )
A.?点A??????????????????????????????????????B.?点B??????????????????????????????????????C.?点C??????????????????????????????????????D.?点D
二、判断题
5.用(x,9)表示位置,不知道在第几行,但知道是第9列。
6.小小的位置在第5行,第8列,用对数表示为(5,8).(判断对错)
7.数对(3,4)和(5,4)表示的位置是在同一行.(判断对错)
8.判断,正确的填“正确”,错误的填“错误”. 把第2排第3个涂上颜色.★在第几排第几个? 答:★在第6排第4个.
三、填空题
9.在确定一个点的位置时,一般都把该点对应的横轴上的数写在________面,把纵轴上的数写在________面.
10.如图,方格纸的每个小方格的边长都是1的正方形,A,B两点在小方格的顶点上,A点的位置可以用(1,1)表示;B点的位置可用(2,3)表示.现在要在小方格的顶点上找到C点,连接AB,AC和BC后得三角形,且三角形ABC的面积为2.请你找出5个符合条件的C点,并在下面用数对表示出各点的位置. C1________,C2________,C3________,C4________,C5________.
11.右图中B点在(4,2),那么A点在________,以AB所在的直线为对称轴,C点的对称点C'的位置是________。
12.学校组织同学们去电影院看电影,聪聪坐在(6,4)的位置,明明坐在(6,2)的位置,亮亮和他们俩坐在同一条直线上,亮亮的位置可能是(________,________)
13.王芳做早操时的位置是(2,4),李立在王芳的后面,中间相隔五个同学,他们都面向南而站.李立的位置是(________,________)
四、解答题
14.下图是某个城镇的示意图,七个伙伴住在城镇的七个不同的地方(图中用圆圈表示)。他们想一起聚会喝咖啡,为使七个人行走的距离总和最小,他们应该在城镇的何处见面?请用“△”在下图中标注出来并用数对表示该点的位置。
15.下面是五一班学生座位平面图
(1)王兵坐在第2列第5行,请你在图中用“△”标出王兵的位置.用数对表示是________.
(2)钟卫的位置是(4,3),在图中是第________列第________行,在平面图中用“☆”标出钟卫的位置.
(3)在平面图中分别用A、B标出(6,4)和(4,6)的位置.
(6,4)和(4,6)表示的位置一样吗?为什么?
(4)赵洪的位置是(3,3).他前面的座位上是王丽,用数对表示是(3,2),后面的座位上是胡小平,左边的座位上是马兵,右边的座位上是李然.请用数对分别表示胡小平、马兵、李然的位置.
五、作图题
16.描出下面各点并连成封闭图形.A(5,9)B(1,6)C(5,6)
六、综合题
17.《汽车司机使用交通图册》中有这样一个“里程速查表”(如图,单位:千米).312国道从南京到上海的8个城市中,任意两个城市之间的公路里程都可以迅速地从该表中查到.比如,查镇江到无锡的公路里程,可以现在表中找到“镇江”,往下看,有一列数;再找到“无锡”,往左看一行数.这一列和一行数的交叉点处的数“122”,就是镇江到无锡的公路里程数.
(1)上海到南京的公路里程是________千米,如果乘坐的汽车行驶的平均速度是80千米/小时,从上海到南京需要________小时.
(2)按照图中的规律可以推算:A=________,B=________.
参考答案
一、单选题
1.【答案】C
【解析】【解答】如果点X的位置为(2,3),则点Y的位置为(5,4). 故答案为:C.
【分析】用数对表示位置的方法是:第一个数字表示列,第二个数字表示行,据此可以得到点Y在第5列第4行,用数对表示为(5,4).
2.【答案】 C
【解析】【解答】解:Y在5列4行,用数对表示是(5,4)。 故答案为:C
【分析】数对中第一个数表示列,第二个数表示行。判断出Y所在的列与行用数对表示出来即可。
3.【答案】C
【解析】【解答】解:我们能用数对表示一些物体的位置。 故答案为:C。
【分析】方向和距离能描述两个物体的相对位置,数对能表示物体的位置,据此解答即可。
4.【答案】 B
【解析】【解答】解:根据如图所建的坐标系,易知(10,20)表示的位置是点B,
故选:B.
【分析】根据题意可得:小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(﹣40,﹣30)表示,即向西走为x轴负方向,向南走为y轴负方向;则(10,20)表示的位置是向东10,北20;即点B所在位置.本题考查了学生利用类比点坐标解决实际问题的能力和阅读理解能力.解决此类问题需要先确定原点的位置,再求未知点的位置,或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
二、判断题
5.【答案】错误
【解析】【解答】用(x,9)表示位置,不知道在第几列,但知道是第9行,原题说法错误. 故答案为:错误. 【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行,据此判断.
6.【答案】错误
【解析】【解答】解:小小的位置在第5行,第8列,用对数表示为(8,5),不是(5,8), 原题说法错误. 故答案为:错误. 【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可确定小小的位置,再与(5,8)比较.
7.【答案】正确
【解析】【解答】解:(3,4)表示第3列第4行,(5,4)表示第5列第4行,它们都表示第4行; 原题说法正确. 故答案为:正确. 【分析】数对表示位置时,第一个数表示列数,第二个数表示行数;所以(3,4)表示第3列第4行,(5,4)表示第5列第4行,据此做出判断.
8.【答案】错误
【解析】【解答】 答:★在第4排第6个. 横为行,也就是排,第几行也就是第几排.第2排应该是第2横行,第3个应该是从左往右数第3个,而不应该是从上往下数第3个.因为第1问在涂颜色时横、竖没有分清楚,所以第2问的答案也不正确.
三、填空题
9.【答案】前;后
【解析】【解答】在确定一个点的位置时,一般都把该点对应的横轴上的数写在前面,把纵轴上的数写在后面. 故答案为:前;后 【分析】写在前面的数也就是数对中第一个数,表示所在的列,第二个数写在后面,表示所在的行.
10.【答案】(3,1);(0,3);(4,3);(5,5);(1,5)
【解析】【解答】解:如图所示: 用数对表示出各点的位置是: C1(3,1);C2(0,3);C3 (4,3);C4 (5,5);C5 (1,5). 故答案为:(3,1);(0,3);(4,3);(5,5);(1,5). 【分析】AB之间的水平距离为2,只要到点A或B等于2的在格点上的点都符合.AB之间的垂直距离为1,只要到点A或B等于4的在格点上的点都符合,再利用数对表示位置的方法即可标出各点的位置.三角形的面积等于底×高÷2,所以只需找到水平距离,或垂直距离,就能得到符合条件的另一点的位置.
11.【答案】(4,5);(3,1)
【解析】【解答】解:A点在4列5行,是(4,5);C′在3列1行,是(3,1). 故答案为:(4,5);(3,1) 【分析】数对中第一个数表示列,第二个数表示行,根据B点的位置确定列与行的计数方法后用数对表示A和C′的位置即可.
12.【答案】6;1
【解析】【解答】学校组织同学们去电影院看电影,聪聪坐在(6,4)的位置,明明坐在(6,2)的位置,亮亮和他们俩坐在同一条直线上,亮亮的位置可能是(6,1),(第2个空答案不唯一). 故答案为:6;1.
【分析】根据题意可知,聪聪、明明、亮亮在同一列,那么它们的列数相同,也就是数对中的第一个数字相同,行数不同,也就是第二个数字不同,据此解答.
13.【答案】2;10
【解析】【解答】如图: 李立的位置是(2,10) 故答案为:2;10 【分析】数对中第一个数表示列,第二个数表示行,后方是北方,确定出李立的位置后用数对表示李立的位置即可.
四、解答题
14.【答案】 解:七个人到竖向最近的位置是七个人的中间位置,在第5竖街区;七个人到横向最近的位置是七个人的中间位置,在第4横街区。故他们应在第5竖街区与第4横街区交会处见面,即(5,4)处。
【解析】【分析】要想七个人行走的距离总和最小,只需要找出行与列的中间位置即可;这些位置中,第一个数最小是2,最大是8,取中间是第5列,第二个数最小是0,最大是7,取中间是第4行,所以他们应在第5竖街区与第4横街区交会处见面,即(5,4)处。
15.【答案】(1)(2,5) (2)4;3 (3)解:位置不一样,(6,4)表示6列4行,(4,6)表示4列6行. (4)解:胡小平是(3,4),马兵是(4,3),李然是(2,3).
【解析】【解答】(1)2列5行用数对表示是(2,5); (2)(4,3)表示在4列3行; (3)根据所在的列与行判断两个位置是否一样; (4)从图中找出三人的位置,并用数对表示出来. 如图: 故答案为:(1)(2,5);(2)4;3;(3)位置不一样,(6,4)表示6列4行,(4,6)表示4列6行;(4)胡小平是(3,4),马兵是(4,3),李然是(2,3).
【分析】数对中第一个数表示列,第二个数表示行,按照这个规律判断出所在的列与行分别解答各个小题即可.
五、作图题
16.【答案】解:根据数对表示位置的方法在平面图中标出各点的位置,并顺次连接起来得出直角三角形ABC如下图所示:
【解析】【分析】用数对表示位置时,第一个数表示第几列,第二个数表示第几行.由此即可标出图中各个点的位置.此题主要考查了数对的意义,即在数对中,第一个数表示第几列,第二个数表示第几行.
六、综合题
17.【答案】(1)352 ;4.4
(2)258 ;94
【解析】【解答】解:(1)由图可知,上海到南京的公路里程是352千米,
根据时间=路程÷速度,从上海到南京所需时间为:352÷80=4.4(小时),
(2)由题意可知:A=南京至无锡的里程数+无锡至苏州的里程数=197+61=258,
B=苏州至昆山的里程数+昆山至上海的里程数=40+54=94.
故答案为:(1)352,4.4;(2)258,94.
【分析】(1)根据题意可知,上海到南京的公路里程数就是上海所对应的一行数与南京所对应的一列数的交叉点处的数,由图可知答案,再根据路程、速度与时间之间的关系,已知路程和速度,求出时间即可;(2)由图可知A表示南京至苏州的公路里程数,B表示苏州至上海的公路里程数.图中的规律可以理解为:甲到丙的里程数=甲到乙的里程数+乙到丙的里程数,因而,A=南京至无锡的里程数+无锡至苏州的里程数,B=苏州至昆山的里程数+昆山至上海的里程数,由图找出相关数据,相加即可.本题考查了数对与位置,要善于根据题意,结合图形,寻找规律.
