六年级下册数学一课一练-1.2正比例(一) 浙教版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-1.2正比例(一) 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 00:00:00 | ||
图片预览


文档简介
六年级下册数学一课一练-1.2正比例(一)
一、单选题
1.在x =7y中,x和y成(?? )
A.?成正比例??????????????????????????????????B.?成反比例??????????????????????????????????C.?不成比例
2.工作效率一定,工作时间和工作总量(?? )
A.?成正比例??????????????????????????B.?成反比例??????????????????????????C.?不成比例??????????????????????????D.?不成正比例
3.下面题中的两个关联的量(?? )
圆柱的高一定,它的底面积和体积.
A.?成正比例??????????????????????????????????B.?成反比例??????????????????????????????????C.?不成比例
二、判断题
4.小新跳高的高度和他的身高成正比例。
5.判断对错
一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例.
6.工作效率一定,工作总量和工作时间成正比例。(判断对错)
7.阳光下同时同地的杆高和影长成正比例。
三、填空题
8.平行四边形的底一定,面积和________成正比例。
9.右图描述了一列动车的行驶情况。
(1)这列动车每小时行驶________千米。
(2)这列动车行驶的路程与时间成________比例。
(3)上虞到上海的铁路里程约240千米。照这样的速度,这列动车从上虞到上海需要行________ 小时。
10.若5:x=3:y,那么x与y成________比例.
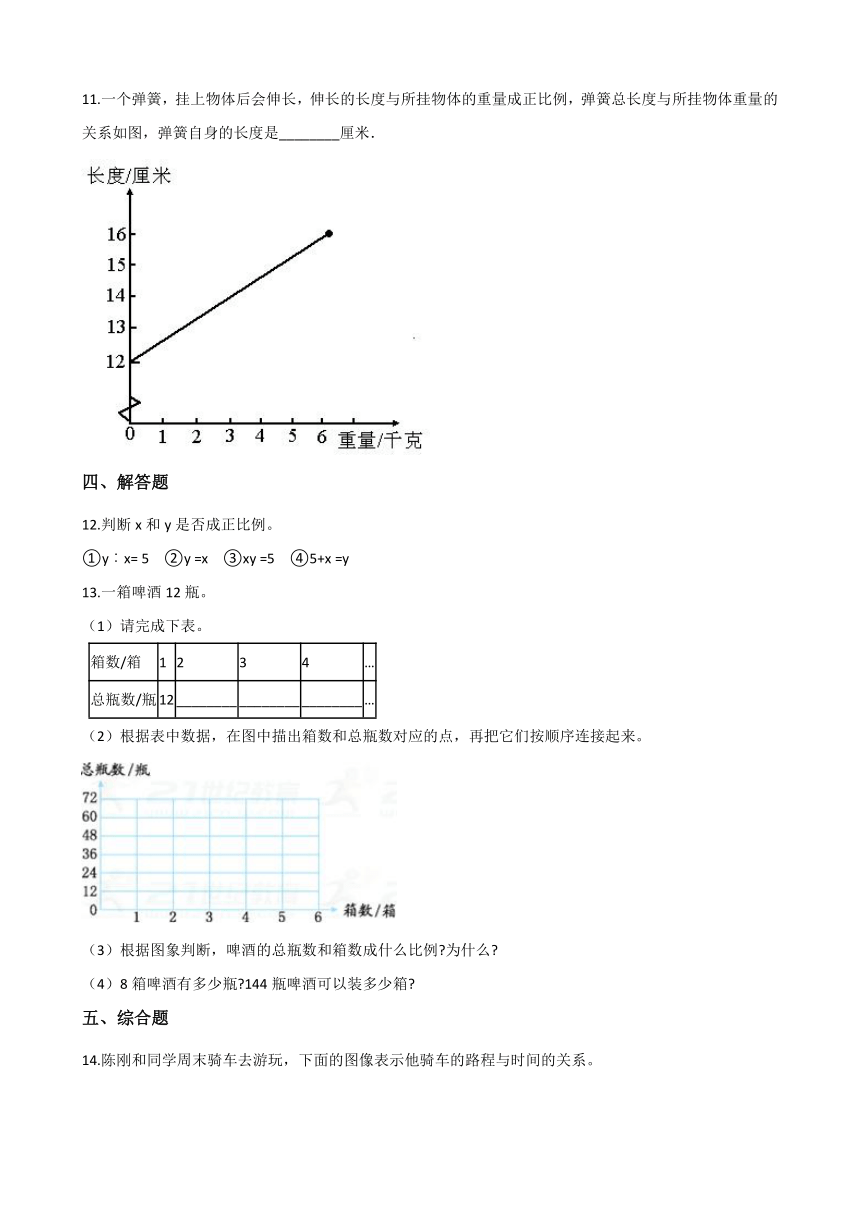
11.一个弹簧,挂上物体后会伸长,伸长的长度与所挂物体的重量成正比例,弹簧总长度与所挂物体重量的关系如图,弹簧自身的长度是________厘米.
四、解答题
12.判断x和y是否成正比例。
①y︰x= 5?? ②y =x?? ③xy =5?? ④5+x =y
13.一箱啤酒12瓶。
(1)请完成下表。
箱数/箱
1
2
3
4
…
总瓶数/瓶
12
________
________
________
…
(2)根据表中数据,在图中描出箱数和总瓶数对应的点,再把它们按顺序连接起来。
(3)根据图象判断,啤酒的总瓶数和箱数成什么比例?为什么?
(4)8箱啤酒有多少瓶?144瓶啤酒可以装多少箱?
五、综合题
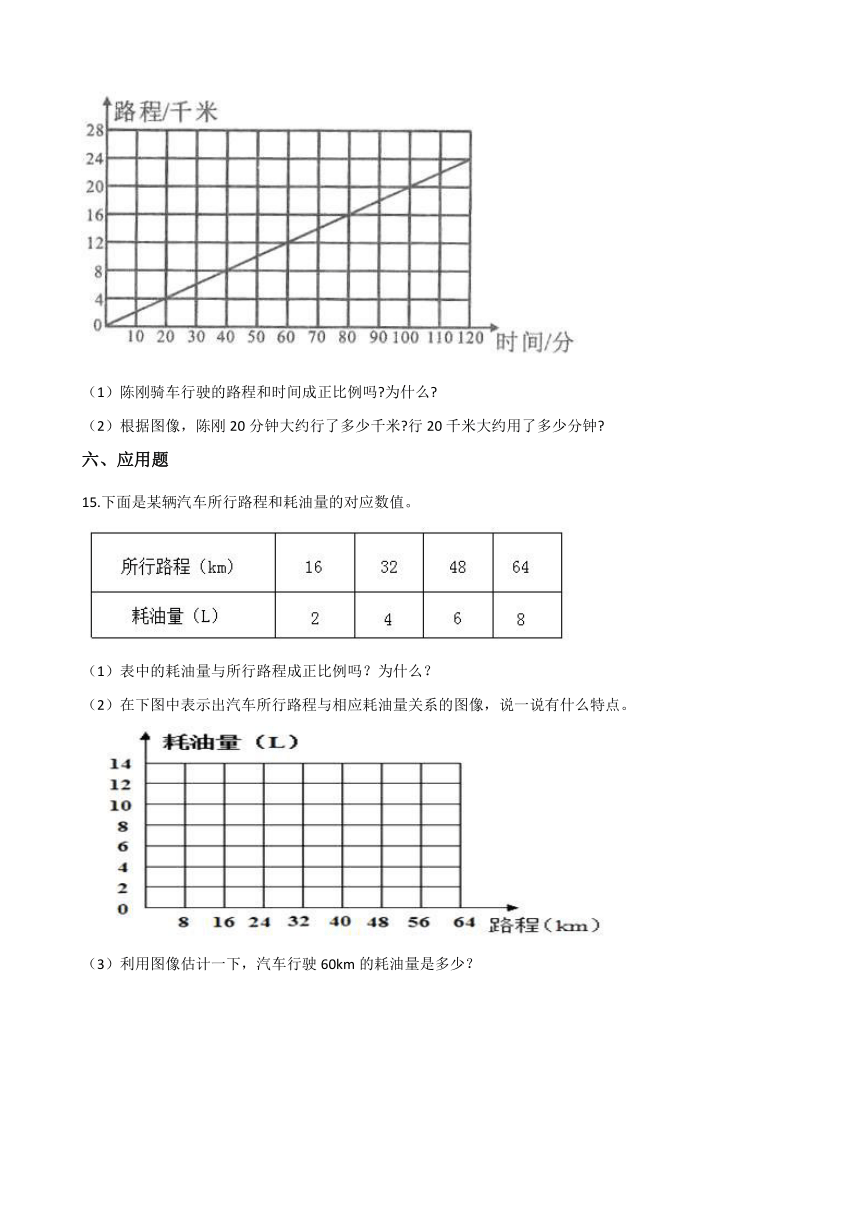
14.陈刚和同学周末骑车去游玩,下面的图像表示他骑车的路程与时间的关系。
(1)陈刚骑车行驶的路程和时间成正比例吗?为什么?
(2)根据图像,陈刚20分钟大约行了多少千米?行20千米大约用了多少分钟?
六、应用题
15.下面是某辆汽车所行路程和耗油量的对应数值。
(1)表中的耗油量与所行路程成正比例吗?为什么?
(2)在下图中表示出汽车所行路程与相应耗油量关系的图像,说一说有什么特点。
(3)利用图像估计一下,汽车行驶60km的耗油量是多少?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】由x =7y可得:x:y=7,x和y成正比例。 故答案为:A。 【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
2.【答案】 A
【解析】【解答】工作总量÷工作时间=工作效率(一定),工作总量与工作时间的商一定,二者成正比例. 故答案为:A
【分析】工作效率一定,先判断工作总量与工作时间的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例.
3.【答案】 A
【解析】【解答】圆柱的高一定,它的底面积和体积成正比例关系. 故答案为:A
【分析]两种相关联的量,一种量变化,另一种量也随着变化,它们的商一定,它们的关系就是正比例关系。
二、判断题
4.【答案】 错误
【解析】【解答】身高高的人跳高不一定比身高低的人跳的高,所以跳高的高度与身高的比值不是定值,因此小新跳高的高度和他的身高不成正比例。
【分析】考察正比例的意义。
5.【答案】 正确
【解析】【解答】解:货物总重量÷运货的次数=一辆车的载重量,载重量一定,货物总重量与运货的次数的商一定,二者成正比例,原题说法正确. 故答案为:正确 【分析】根据数量关系判断运货总重量与运的次数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
6.【答案】 正确
【解析】【解答】因为工作效率×工作时间=工作总量, 所以工作总量:工作时间=工作效率(一定), 可以看出,工作总量和工作时间是两种相关联的量,工作总量随工作时间的变化而变化, 工作效率一定,也就是工作总量和工作时间相对应数的比值一定,所以工作总量和工作时间成正比例关系. 故答案为:正确.
【分析】本题考点:正比例和反比例的意义. 此题重点考查正比例和反比例的意义.
根据正反比例的意义,分析数量关系.既然工作效率一定,那么就看那两个变量(工作总量和工作时间)是比值一定还是乘积一定,从而判定成什么比例关系.
7.【答案】 正确
【解析】【解答】解:同时同地的杆高和影长的商一定,二者成正比例,原题说法正确. 故答案为:正确
【分析】判断出同时同地杆高和影长的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例.
三、填空题
8.【答案】 高
【解析】【解答】根据正比例的基本意义,成正比例的两个量比值一定,而对于平行四边形面积与高的比值为底,所以答案应该为高。
【分析】考察正比例的意义。
9.【答案】 (1)120 (2)正 (3)2
【解析】【解答】解:(1)6分=0.1小时,速度:12÷0.1=120(千米/小时); (2)路程与时间的图像是一条直线,根据正比例图像可知,路程和时间成正比例; (3)240÷120=2(小时) 故答案为:120;正;2
【分析】(1)6分钟行驶了12千米,先把6分钟换算成时,然后用路程除以时间求出速度;(2)根据图像的形状判断正反比例;(3)用路程除以速度求出时间.
10.【答案】 正
【解析】【解答】解:5:x=3:y,那么3x=5y,x:y= (一定)
是x和y对应的比值一定,符合正比例的意义,所以x和y成正比例.
故答案为:正.
【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
11.【答案】 12
【解析】【解答】解:当重量是0千克时,弹簧的长度是12厘米,所以弹簧自身的长度就是12厘米. 故答案为:12
【分析】横轴表示重量,纵轴表示弹簧长度,判断出重量为0时弹簧的长度就是弹簧自身的长度.
四、解答题
12.【答案】 成正比例,成正比例,不成正比例,不成正比例
【解析】【解答】根据正比例的基本意义,成正比例的两个相关联的量比值一定,①中两个量比值为5,是定值,所以成正比例;②中两个量比值为1,是定值,所以成正比例;③中两个量乘积为定值,所以不成正比例;④中两个量的差为定值,所以不成正比例。
【分析】考察正比例的意义。
13.【答案】 (1)24;36;48 (2)解: (3)解:正比例,原因:它们的比值一定。 (4)解:8箱啤酒有96瓶,144瓶啤酒可以装12箱。
【解析】【解答】解:(1)2箱有2×12=24(瓶),3箱有3×12=36(瓶),4箱有4×12=48(瓶); (2)如图: ; (3)由图象可知,啤酒的总瓶数和箱数的商是一定的,所以它们成正比例关系; (4)8箱有8×12=96(瓶),144瓶可以装:144÷12=12(箱)。 【分析】(1)总瓶数=每箱装啤酒的数量×箱数,箱数=总瓶数÷每箱装啤酒的数量。 (2)判断两种量成正比例还是反比例的办法:当这两种相关联的量中相对应的两个数的商一定时,这两个数就成正比例关系;反之,当这两个数的积一定时,这两个数就成反比例关系。
五、综合题
14.【答案】 (1)解:成正比例, =速度(一定). (2)解:20分钟大约行了4千米,行20千米大约用100分钟.
【解析】【分析】(1)这个图像是一条经过原点的直线,是正比例的图像;(2)根据图中20分钟和20千米对应的路程和时间解答.
六、应用题
15.【答案】 (1)解:16÷2=8(km),32÷4=8(km),64÷8=8(km) 答:耗油量与所行的路程成正比例,因为行驶路程与耗油量的比值一定. (2)解:如下图,图像是一条直线.
(3)解:估计汽车行驶60km的耗油量是7.5L.
【解析】【分析】(1)根据表格中的数据判断两个量的商一定还是乘积一定即可判断成什么比例;(2)先描出对应的点再画出图像;(3)根据统计图找出60km对应的耗油量即可做出估计.
一、单选题
1.在x =7y中,x和y成(?? )
A.?成正比例??????????????????????????????????B.?成反比例??????????????????????????????????C.?不成比例
2.工作效率一定,工作时间和工作总量(?? )
A.?成正比例??????????????????????????B.?成反比例??????????????????????????C.?不成比例??????????????????????????D.?不成正比例
3.下面题中的两个关联的量(?? )
圆柱的高一定,它的底面积和体积.
A.?成正比例??????????????????????????????????B.?成反比例??????????????????????????????????C.?不成比例
二、判断题
4.小新跳高的高度和他的身高成正比例。
5.判断对错
一辆汽车的载重量一定,运送货物的总重量和运的次数成正比例.
6.工作效率一定,工作总量和工作时间成正比例。(判断对错)
7.阳光下同时同地的杆高和影长成正比例。
三、填空题
8.平行四边形的底一定,面积和________成正比例。
9.右图描述了一列动车的行驶情况。
(1)这列动车每小时行驶________千米。
(2)这列动车行驶的路程与时间成________比例。
(3)上虞到上海的铁路里程约240千米。照这样的速度,这列动车从上虞到上海需要行________ 小时。
10.若5:x=3:y,那么x与y成________比例.
11.一个弹簧,挂上物体后会伸长,伸长的长度与所挂物体的重量成正比例,弹簧总长度与所挂物体重量的关系如图,弹簧自身的长度是________厘米.
四、解答题
12.判断x和y是否成正比例。
①y︰x= 5?? ②y =x?? ③xy =5?? ④5+x =y
13.一箱啤酒12瓶。
(1)请完成下表。
箱数/箱
1
2
3
4
…
总瓶数/瓶
12
________
________
________
…
(2)根据表中数据,在图中描出箱数和总瓶数对应的点,再把它们按顺序连接起来。
(3)根据图象判断,啤酒的总瓶数和箱数成什么比例?为什么?
(4)8箱啤酒有多少瓶?144瓶啤酒可以装多少箱?
五、综合题
14.陈刚和同学周末骑车去游玩,下面的图像表示他骑车的路程与时间的关系。
(1)陈刚骑车行驶的路程和时间成正比例吗?为什么?
(2)根据图像,陈刚20分钟大约行了多少千米?行20千米大约用了多少分钟?
六、应用题
15.下面是某辆汽车所行路程和耗油量的对应数值。
(1)表中的耗油量与所行路程成正比例吗?为什么?
(2)在下图中表示出汽车所行路程与相应耗油量关系的图像,说一说有什么特点。
(3)利用图像估计一下,汽车行驶60km的耗油量是多少?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】由x =7y可得:x:y=7,x和y成正比例。 故答案为:A。 【分析】如果用字母x和y表示两种相关联的量,用k表示它们的比值,正比例关系可以用以下关系式表示:y:x=k(一定);如果用字母x和y表示两种相关联的量,用k表示它们的积,反比例关系可以用下面关系式表示:xy=k(一定),据此判断。
2.【答案】 A
【解析】【解答】工作总量÷工作时间=工作效率(一定),工作总量与工作时间的商一定,二者成正比例. 故答案为:A
【分析】工作效率一定,先判断工作总量与工作时间的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例.
3.【答案】 A
【解析】【解答】圆柱的高一定,它的底面积和体积成正比例关系. 故答案为:A
【分析]两种相关联的量,一种量变化,另一种量也随着变化,它们的商一定,它们的关系就是正比例关系。
二、判断题
4.【答案】 错误
【解析】【解答】身高高的人跳高不一定比身高低的人跳的高,所以跳高的高度与身高的比值不是定值,因此小新跳高的高度和他的身高不成正比例。
【分析】考察正比例的意义。
5.【答案】 正确
【解析】【解答】解:货物总重量÷运货的次数=一辆车的载重量,载重量一定,货物总重量与运货的次数的商一定,二者成正比例,原题说法正确. 故答案为:正确 【分析】根据数量关系判断运货总重量与运的次数的商一定还是积一定,如果商一定就成正比例,如果积一定就成反比例,否则不成比例.
6.【答案】 正确
【解析】【解答】因为工作效率×工作时间=工作总量, 所以工作总量:工作时间=工作效率(一定), 可以看出,工作总量和工作时间是两种相关联的量,工作总量随工作时间的变化而变化, 工作效率一定,也就是工作总量和工作时间相对应数的比值一定,所以工作总量和工作时间成正比例关系. 故答案为:正确.
【分析】本题考点:正比例和反比例的意义. 此题重点考查正比例和反比例的意义.
根据正反比例的意义,分析数量关系.既然工作效率一定,那么就看那两个变量(工作总量和工作时间)是比值一定还是乘积一定,从而判定成什么比例关系.
7.【答案】 正确
【解析】【解答】解:同时同地的杆高和影长的商一定,二者成正比例,原题说法正确. 故答案为:正确
【分析】判断出同时同地杆高和影长的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例.
三、填空题
8.【答案】 高
【解析】【解答】根据正比例的基本意义,成正比例的两个量比值一定,而对于平行四边形面积与高的比值为底,所以答案应该为高。
【分析】考察正比例的意义。
9.【答案】 (1)120 (2)正 (3)2
【解析】【解答】解:(1)6分=0.1小时,速度:12÷0.1=120(千米/小时); (2)路程与时间的图像是一条直线,根据正比例图像可知,路程和时间成正比例; (3)240÷120=2(小时) 故答案为:120;正;2
【分析】(1)6分钟行驶了12千米,先把6分钟换算成时,然后用路程除以时间求出速度;(2)根据图像的形状判断正反比例;(3)用路程除以速度求出时间.
10.【答案】 正
【解析】【解答】解:5:x=3:y,那么3x=5y,x:y= (一定)
是x和y对应的比值一定,符合正比例的意义,所以x和y成正比例.
故答案为:正.
【分析】判定两种量是否成正、反比例,要看这两种量是对应的比值一定,还是对应的乘积一定,如果是比值一定就成正比例;如果是乘积一定,就成反比例.
11.【答案】 12
【解析】【解答】解:当重量是0千克时,弹簧的长度是12厘米,所以弹簧自身的长度就是12厘米. 故答案为:12
【分析】横轴表示重量,纵轴表示弹簧长度,判断出重量为0时弹簧的长度就是弹簧自身的长度.
四、解答题
12.【答案】 成正比例,成正比例,不成正比例,不成正比例
【解析】【解答】根据正比例的基本意义,成正比例的两个相关联的量比值一定,①中两个量比值为5,是定值,所以成正比例;②中两个量比值为1,是定值,所以成正比例;③中两个量乘积为定值,所以不成正比例;④中两个量的差为定值,所以不成正比例。
【分析】考察正比例的意义。
13.【答案】 (1)24;36;48 (2)解: (3)解:正比例,原因:它们的比值一定。 (4)解:8箱啤酒有96瓶,144瓶啤酒可以装12箱。
【解析】【解答】解:(1)2箱有2×12=24(瓶),3箱有3×12=36(瓶),4箱有4×12=48(瓶); (2)如图: ; (3)由图象可知,啤酒的总瓶数和箱数的商是一定的,所以它们成正比例关系; (4)8箱有8×12=96(瓶),144瓶可以装:144÷12=12(箱)。 【分析】(1)总瓶数=每箱装啤酒的数量×箱数,箱数=总瓶数÷每箱装啤酒的数量。 (2)判断两种量成正比例还是反比例的办法:当这两种相关联的量中相对应的两个数的商一定时,这两个数就成正比例关系;反之,当这两个数的积一定时,这两个数就成反比例关系。
五、综合题
14.【答案】 (1)解:成正比例, =速度(一定). (2)解:20分钟大约行了4千米,行20千米大约用100分钟.
【解析】【分析】(1)这个图像是一条经过原点的直线,是正比例的图像;(2)根据图中20分钟和20千米对应的路程和时间解答.
六、应用题
15.【答案】 (1)解:16÷2=8(km),32÷4=8(km),64÷8=8(km) 答:耗油量与所行的路程成正比例,因为行驶路程与耗油量的比值一定. (2)解:如下图,图像是一条直线.
(3)解:估计汽车行驶60km的耗油量是7.5L.
【解析】【分析】(1)根据表格中的数据判断两个量的商一定还是乘积一定即可判断成什么比例;(2)先描出对应的点再画出图像;(3)根据统计图找出60km对应的耗油量即可做出估计.
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
