北师大版七年级数学下册4.3《探索三角形全等的条件》课件(共25张)
文档属性
| 名称 | 北师大版七年级数学下册4.3《探索三角形全等的条件》课件(共25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
情境问题:
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?
想一想:
要画一个三角形与小颖画的三角形全等,需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
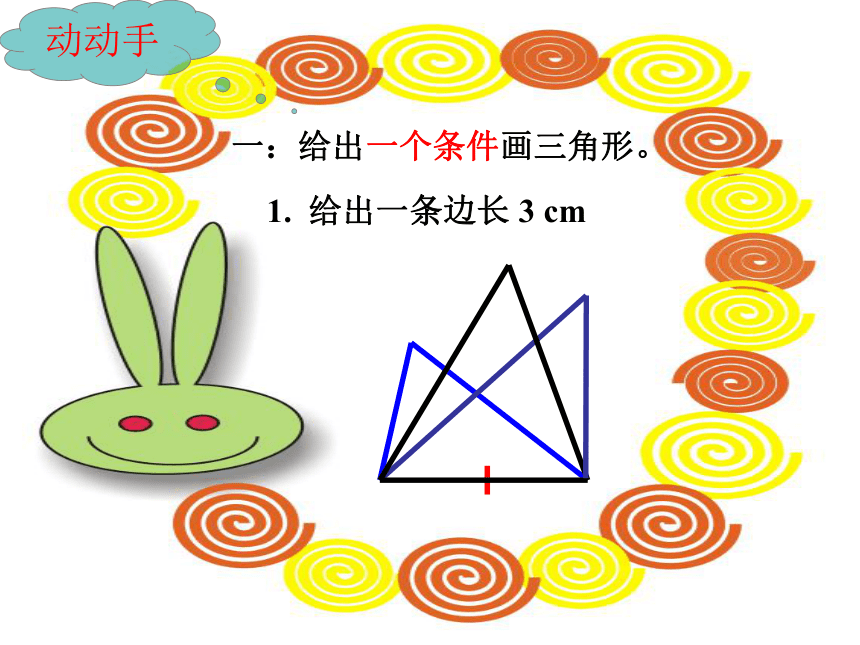
一:给出一个条件画三角形。
1. 给出一条边长 3 cm
动动手
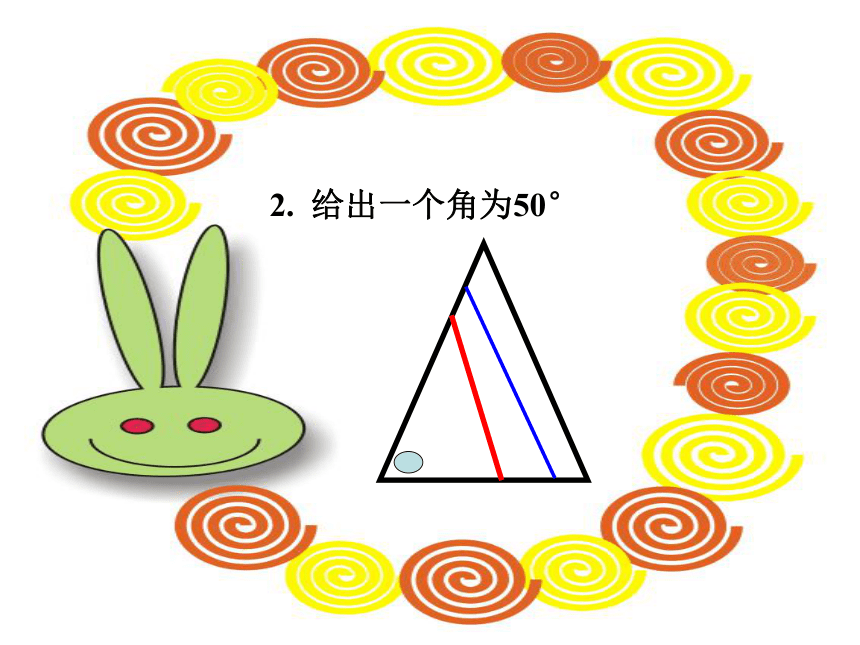
2. 给出一个角为50°
二:给出两个条件画三角形。
(1) 两个角
(2) 两条边
(3)一条边和一个角
2、按照下面给出的两个条件画出三角形,并与小组其他同学的比一比
(3)三角形的一个角为 30°,一条边为6cm ;
分组探究活动
(2)三角形的两条边分别是 4cm 和 6cm ;
(1)三角形的两个角分别是 30°和 60°.
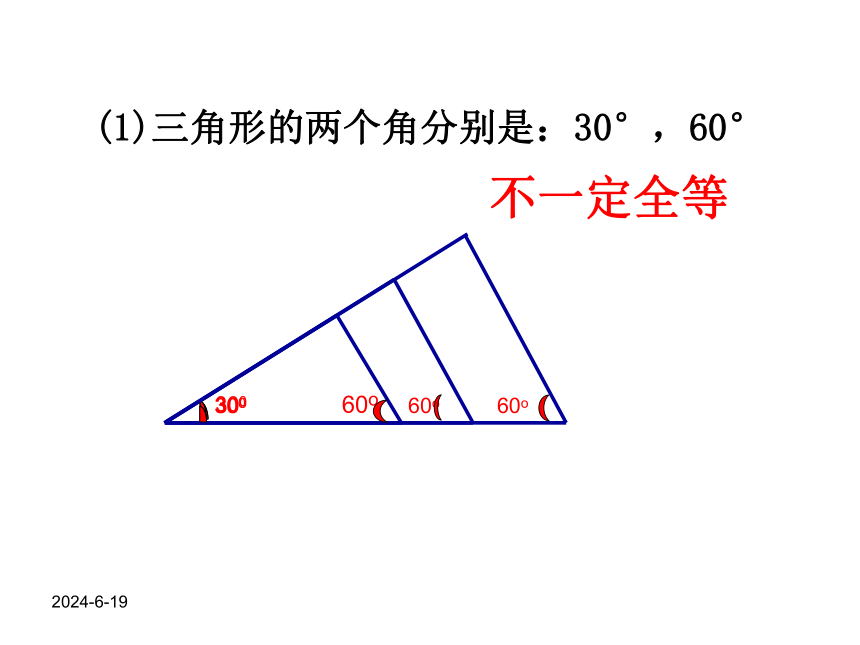
(1)三角形的两个角分别是:30°,60°
不一定全等
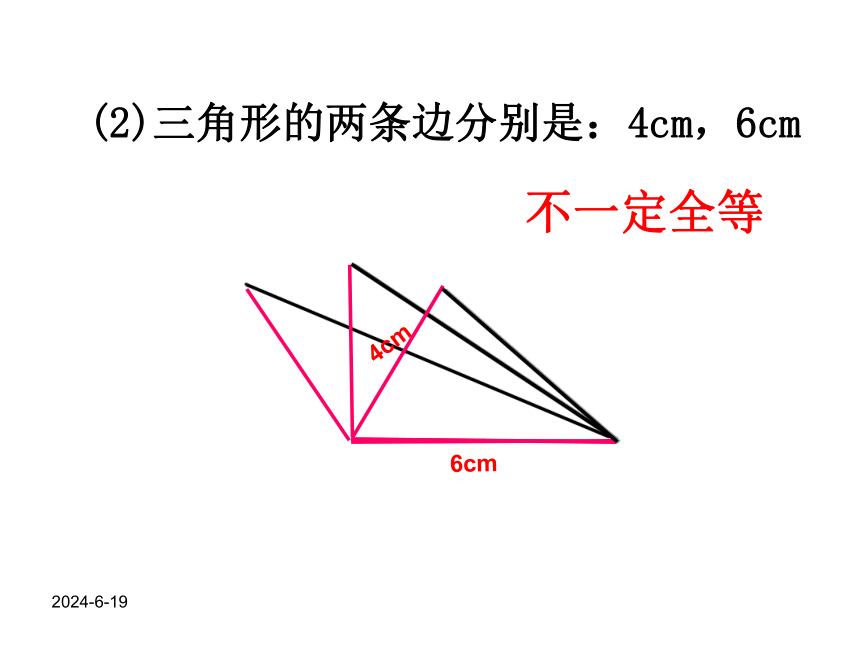
(2)三角形的两条边分别是:4cm,6cm
不一定全等
(3) 三角形的一个角为30°,一条边为6cm
不一定全等
只给出一个条件或两个条件时,
都不能保证所画出的三角形全等.
总结结论:
三:议一议
若给出三个条件画三角形,你能说出有哪几中可能情况?
都给角:给三个角
2. 都给边:给三条边
3.既给角,又给边:
给两条边,一个角
给一条边,两个角
(1)
(2)
已知一个三角形的三个内角 分别为400,600,800,请画出这个三角形。
结论:三个内角对应相等的两个三角形不一定全等.
1.给出三个角
已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
2.给出三条边
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”
2.给出三条边
几何表述:
在△ABC和△EFG中
AB=EF
BC=FG
AC=EG
∴
(SSS)
A
B
C
D
应用:
例1:已知:AB=CB,AD=CD。
求证:△ABD≌△CBD
练习
如图,AB=DC,AF=DE,BE=CF.
求证:∠A=∠D
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
准备若干长度适中的小木条,用其中三根 木条钉成一个三角形的框架,它的形状和大小是固定的吗?如果用四根小木条钉成的框架形状和大小固定吗?
四:做一做
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
(1)三角形全等的条件1:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
(2)三角形具有稳定性.
情境问题:
小颖作业本上画的三角形被墨迹污染了,她想画一个与原来完全一样的三角形,她该怎么办?请你帮助小颖想一个办法,并说明你的理由?
想一想:
要画一个三角形与小颖画的三角形全等,需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
一:给出一个条件画三角形。
1. 给出一条边长 3 cm
动动手
2. 给出一个角为50°
二:给出两个条件画三角形。
(1) 两个角
(2) 两条边
(3)一条边和一个角
2、按照下面给出的两个条件画出三角形,并与小组其他同学的比一比
(3)三角形的一个角为 30°,一条边为6cm ;
分组探究活动
(2)三角形的两条边分别是 4cm 和 6cm ;
(1)三角形的两个角分别是 30°和 60°.
(1)三角形的两个角分别是:30°,60°
不一定全等
(2)三角形的两条边分别是:4cm,6cm
不一定全等
(3) 三角形的一个角为30°,一条边为6cm
不一定全等
只给出一个条件或两个条件时,
都不能保证所画出的三角形全等.
总结结论:
三:议一议
若给出三个条件画三角形,你能说出有哪几中可能情况?
都给角:给三个角
2. 都给边:给三条边
3.既给角,又给边:
给两条边,一个角
给一条边,两个角
(1)
(2)
已知一个三角形的三个内角 分别为400,600,800,请画出这个三角形。
结论:三个内角对应相等的两个三角形不一定全等.
1.给出三个角
已知三角形三条边分别是 4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?
2.给出三条边
三边对应相等的两个三角形全等,
简写为“边边边”或“SSS”
2.给出三条边
几何表述:
在△ABC和△EFG中
AB=EF
BC=FG
AC=EG
∴
(SSS)
A
B
C
D
应用:
例1:已知:AB=CB,AD=CD。
求证:△ABD≌△CBD
练习
如图,AB=DC,AF=DE,BE=CF.
求证:∠A=∠D
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
准备若干长度适中的小木条,用其中三根 木条钉成一个三角形的框架,它的形状和大小是固定的吗?如果用四根小木条钉成的框架形状和大小固定吗?
四:做一做
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
(1)三角形全等的条件1:三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.
(2)三角形具有稳定性.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
