北京课改版九年级数学上册第21章 《圆(上)》 综合测试卷(含答案)
文档属性
| 名称 | 北京课改版九年级数学上册第21章 《圆(上)》 综合测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 19:26:50 | ||
图片预览



文档简介
北京版九年级数学上册
第21章 圆(上)
综合测试卷
(时间90分钟,满分120分)
一.选择题(本大题共10小题,每小题3分,共30分)
1.如图,在半径为5的⊙O中,弦AB=8,OP⊥AB,垂足为点P,则OP的长为( )
A.4 B.5 C.3 D.2
2.如图,在⊙O中,=2,则下列结论正确的是( )
A.AB>2CD B.AB=2CD
C.AB<2CD D.以上都不正确
3.如图,AB是⊙O的直径,若∠BAC=25°,则∠ADC的大小是( )
A.55° B.65° C.75° D.85°
4.已知点O为△ABC的外心,若∠A=80°,则∠BOC的度数为( )
A.40° B.80° C.160° D.120°
5.如图,A,B,C,D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40° B.45° C.50° D.55°
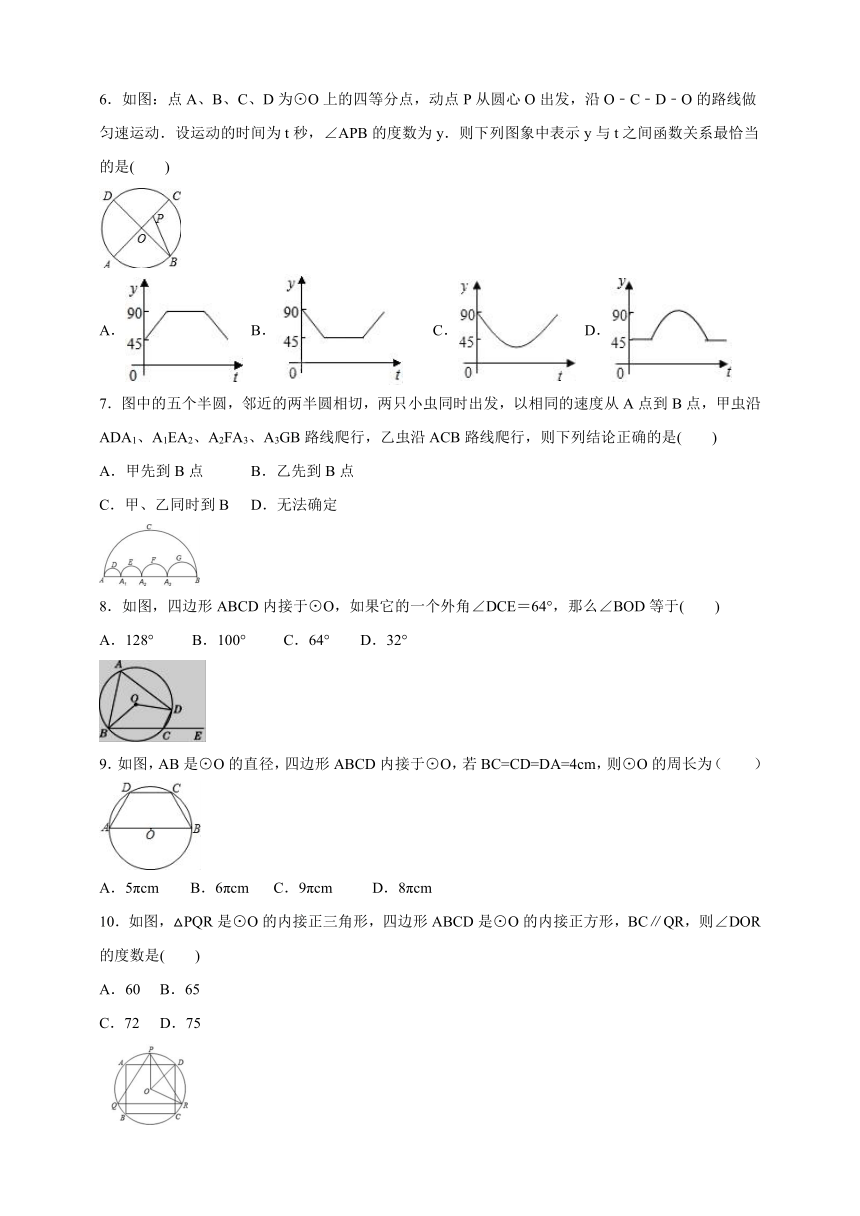
6.如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. B. C. D.
7.图中的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行,乙虫沿ACB路线爬行,则下列结论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B D.无法确定
8.如图,四边形ABCD内接于⊙O,如果它的一个外角∠DCE=64°,那么∠BOD等于( )
A.128° B.100° C.64° D.32°
9.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为( )
A.5πcm B.6πcm C.9πcm D.8πcm
10.如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠DOR的度数是( )
A.60 B.65
C.72 D.75
二.填空题(共8小题,3*8=24)
11.如图,在⊙O中,弦AB与弦CD相等,则______.(填>、<或=)
12. 如图,扇形OAB的圆心角为122°,C是上一点,则∠ACB=_________.
13. 如图,在△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,则图中阴影部分的面积为____________(结果保留π).
14.如图,AB为⊙O的直径,延长AB至点D,使BD=OB,DC切⊙O于点C,点B是的中点,弦CF交AB于点E.若⊙O的半径为2,则CF=________.
15.如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为 _________ .
16.如图,△ABC内接于⊙O,∠B=∠OAC,OA=8cm,则AC= cm.
17. 如图,E是半径为2 cm的⊙O的直径CD延长线上的一点,AB∥CD且AB=CD,则阴影部分的面积是__________.
18.如图,在三角尺ABC中,∠ACB=90°,∠ABC=30°,BC=6,三角尺绕直角顶点C逆时针旋转,当点A的对应点A′落在AB边上时即停止转动,则点B转过的路径长为________.
三.解答题(共7小题,66分)
19.(8分) 如图,以等边三角形ABC的边BC为直径作⊙O交AB于点D,交AC于点E.试判断BD,DE,EC之间的大小关系,并说明理由.
20.(8分) 如图,一个量角器所在圆的直径为10 cm,其外缘有A,B两点,其读数分别为71°和47°.
(1)劣弧AB所对圆心角是多少度?
(2)求的长;
(3)问A,B之间的距离是多少?
(参考数据:sin12°≈0.21,cos12°≈0.98)
21.(8分) 如图,AB,CD是⊙O的弦,AB⊥CD,BE是⊙O的直径,若AC=3,求DE的长.
22.(10分) 等边三角形ABC的顶点A,B,C在⊙O上,D为⊙O上一点,且BD=CD,如图所示,判断四边形OBDC是哪种特殊四边形,并说明理由.
23.(10分) 某地有一座弧形的拱桥,桥下的水面宽度为7.2 m,拱顶高出水面2.4 m,现有一艘宽3 m,船舱顶部为长方形并高出水面2 m的货船要经过这里,此货船能顺利通过这座拱桥吗?
24.(10分) 已知A、B、C、D是⊙O上的四个点.
(1)如图①,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图②,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
25.(12分) 如图,已知在△ABC中,∠ABC=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
参考答案:
1-5 CCBCB 6-10 BCADD
11. =
12. 119°
13.4-π
14.2
15. (2,0)
16. 8
17. π cm2
18.2π
19.解:BD=DE=EC.理由如下:
连接OD,OE.
∵OB=OD=OE=OC,∠B=∠C=60°,
∴△BOD与△COE都是等边三角形.
∴∠BOD=∠COE=60°,
∴∠DOE=180°-∠BOD-∠COE=60°.
∴∠DOE=∠BOD=∠COE.∴BD=DE=EC.
20. 解:(1)∠AOB=71°-47°=24°.
(2)l===π(cm).
(3)连接AB,过点O作OD⊥AB于点D,则∠AOD=∠BOD=12°,sin 12°=,
∴AD≈5×0.21=1.05(cm).∴AB=2.1 cm.
21. 解:∵BE是⊙O的直径,
∴∠BDE=90°.
∴∠BDC+∠CDE=90°.
又∵AB⊥CD,
∴∠ACD+∠CAB=90°.
∵∠CAB=∠BDC,
∴∠ACD=∠CDE.
∴=.
∴-=-.
∴=.∴DE=AC=3.
22.解:四边形OBDC是菱形,理由如下:
连接AD,设AD与BC交于P点,
∵AB=AC,∴=.
同理=,∴+=+,
即和都是半圆.
∴AD为⊙O的直径,即AD过圆心O.
∵AB=BC=CA,∴∠AOB=∠BOC=∠COA=120°.
∴∠BOD=∠COD=60°.
∴OB=OD=BD,OC=CD=DO.
∴OB=OC=BD=CD,∴四边形OBDC是菱形.
23.解:如图,设弧形拱桥AB所在圆的圆心为O,连接OA,OB,ON,作OD⊥AB于点D,交⊙O于点C,交MN于点H,由垂径定理可知,D为AB的中点.
设OA=r m,则OD=OC-DC=(r-2.4) m,AD=AB=3.6 m.
在Rt△AOD中,OA2=AD2+OD2,
即r2=3.62+(r-2.4)2,解得r=3.9.
在Rt△OHN中,OH===3.6(m).
所以FN=DH=OH-OD=3.6-(3.9-2.4)=2.1(m).
因为2.1 m>2 m,所以此货船能顺利通过这座拱桥.
24.(1)证明:∵∠ADC=∠BCD=90°,∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,∴四边形ABCD是矩形,
∵AD=CD,∴四边形ABCD是正方形,
∴AC⊥BD.
(2)解:如图,作直径DF,连结CF、BF,
∵DF是直径,∴∠DCF=∠DBF=90°,∴FB⊥DB,
又∵AC⊥BD.∴BF∥AC,∴=,∴CF=AB.
根据勾股定理,得DF2=CF2+DC2=AB2+DC2=20,
∴DF=2,∴OD=,
即⊙O的半径为.
25.(1)证明:如图,连结DE,
∵AE是⊙O的直径,
∴∠ADE=90°.
∴∠ADE=∠ABC.
在Rt△ADE和Rt△ABC中,∠A是公共角,
∴△ADE∽△ABC.
∴=,即AC·AD=AB·AE.
(2)解:如图,连结OD,
∵BD是⊙O的切线,∴OD⊥BD.
在Rt△OBD中,OE=BE=OD,
∴OB=2OD,∴∠OBD=30°.
易知∠BAC=30°,
在Rt△ABC中,AC=2BC=2×2=4.
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
