人教版数学九年级下册:28.1锐角三角函数 课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级下册:28.1锐角三角函数 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-23 23:32:36 | ||
图片预览





文档简介
(共24张PPT)
亲爱的同学们
欢迎走进
数学天地
1、理解并掌握三角函数的定义,并用它解决直角 三角形的边角关系。
2、能够综合运用直角三角形的边角关系解决生活 中的实际问题。
3、通过本节课的学习深化三角函数的内涵,感悟在中考中的重要性。
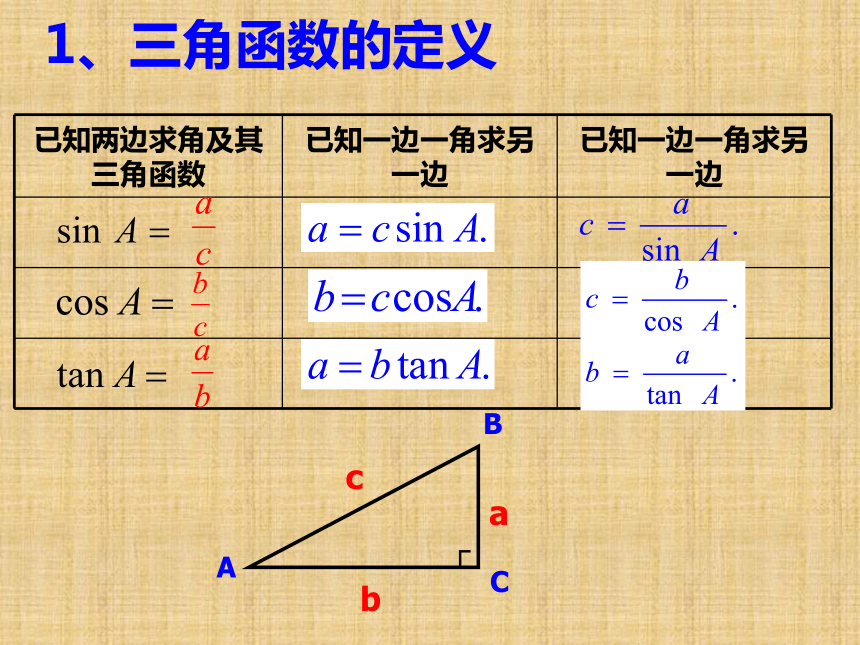
1、三角函数的定义
b
a
c
已知两边求角及其三角函数 已知一边一角求另一边 已知一边一角求另一边
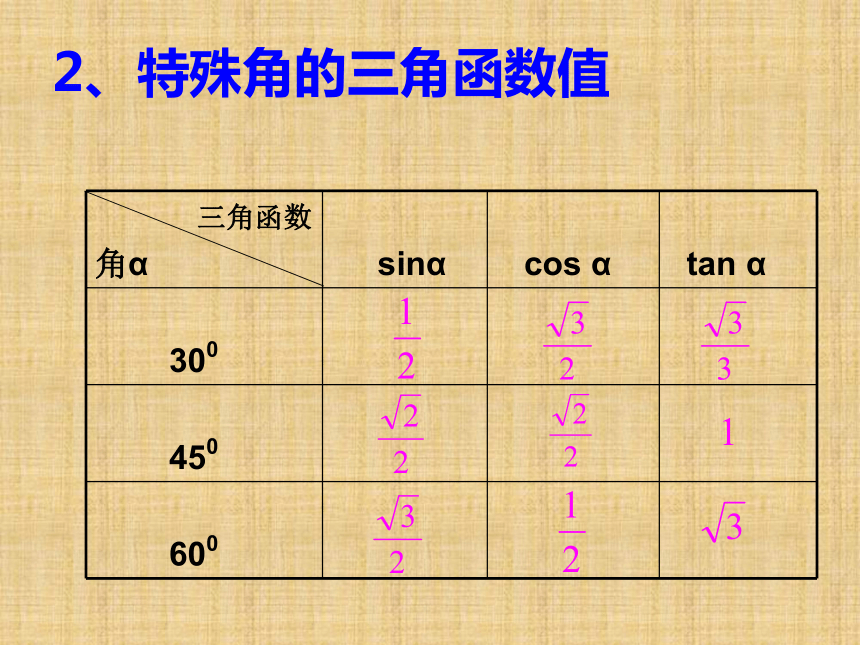
2、特殊角的三角函数值
三角函数
角α
sinα
cos α
tan α
300
450
600
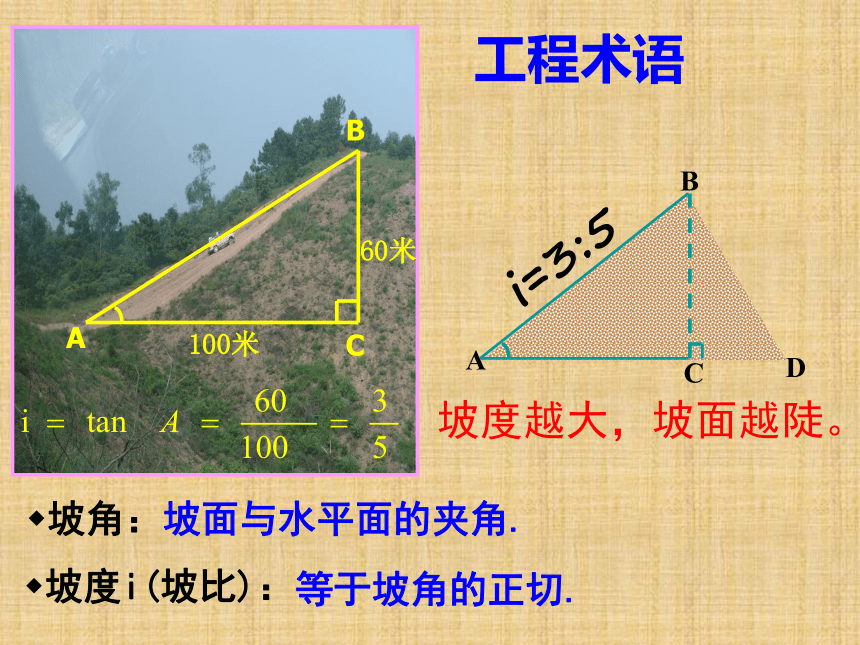
坡角:坡面与水平面的夹角.
坡度越大,坡面越陡。
坡度i(坡比):
工程术语
i=3:5
等于坡角的正切.
1.在Rt△ABC中,各边都扩大5倍,则角A的三角函数值( )
A.不变 B.扩大5倍
C.缩小5倍 D.不能确定
A
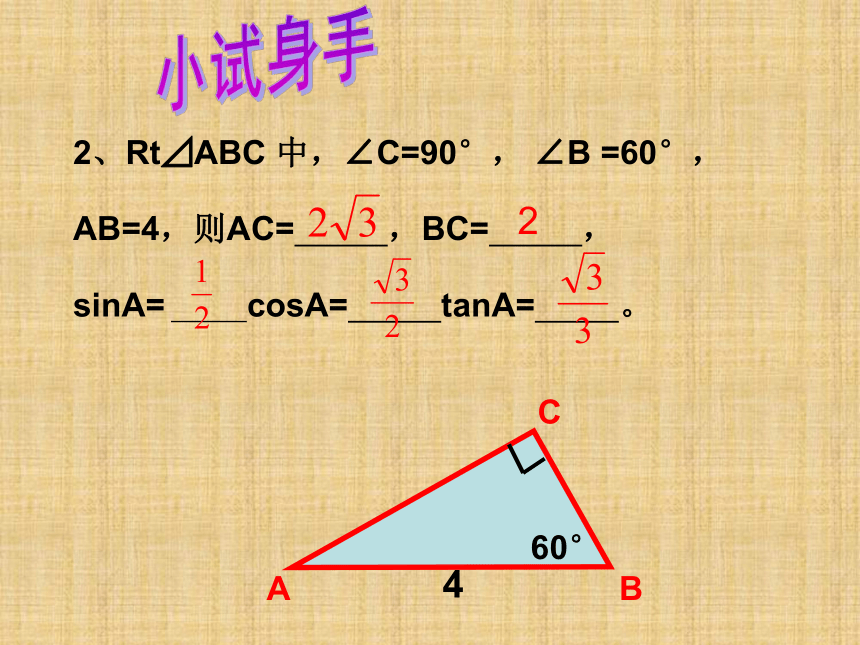
2、Rt⊿ABC 中,∠C=90°, ∠B =60°,
AB=4,则AC= ,BC= ,
sinA= cosA= tanA= 。
2
3.Rt△ABC中,∠ACB = 90°,
CD⊥AB 于D,AC=5,AB=6,则
sin∠1= .
4.Rt△ABC中,∠ACB = 90°,CD
是AB边上的中线,若AC=5,AB=6,
则sin∠1= 。
1
5.如图,沿AC方向开山修路,为加快施工进度,要在山的另一边同时施工,现在从AC上取一点B,使 ∠ ABD=140°,BD=500米,∠D=50°,要使A、C、E在一条直线上,那么点E、D间的距离应为( )
B
B、500cos50°米
A.500sin50°米
C.500tan50°米
6.某地夏季中午,当太阳移到屋顶上方偏东时,光线与地面成α角,房屋朝南的窗子高AB=h米,要在窗子外面上方安装一个水平挡光板AC,使午间光线不能直接射人室内如图1-1-18,那么挡光板AC的宽度为=_____.
锐角三角形????
直角三角形
钝角三角形?
等腰三角形
8.如图铁路路基横断面为一个等腰梯形, 若腰的坡度为2:3,顶宽为3米,路基高为4米,则路基的下底宽是____
坡度
A
A.15米 B.12米
C.9米 D.7米
如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸取两点B、C,测得∠ABC = 45°,∠ACB = 31°,量得BC长为20米。求小河的宽度。(参考数值:tan31°≈ ,sin31°≈ )
20
45°
31°
如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸取两点B、C,测得∠ABM= 45°,∠ACB = 31°,量得BC长为20米。求小河的宽度。(参考数值:tan31°≈ ,sin31°≈ )
45°
31°
20
变式练习1
45°
31°
20
5
变式练习2
45°
31°
20
5
一题多解
(2)精确值(有效数字,保留数位、提供的参考值)
(6分)
(1)转化成基本模型
1、某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40?减至35?.已知原楼梯AB长为5m,调整后的楼梯所占地面CD有多长?
参考数据:
sin40?≈0.64,
cos40?≈0.77,
sin35?≈0.57,
tan35?≈0.70)
(结果精确到0.1m)
B
37°
48°
D
C
A
第19题图
2、小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.
参考数据:
(结果保留整数)
E
本节课学习了哪些知识?
领悟到哪些解决问题的方法?
学习体会
祝同学们
学习进步!
亲爱的同学们
欢迎走进
数学天地
1、理解并掌握三角函数的定义,并用它解决直角 三角形的边角关系。
2、能够综合运用直角三角形的边角关系解决生活 中的实际问题。
3、通过本节课的学习深化三角函数的内涵,感悟在中考中的重要性。
1、三角函数的定义
b
a
c
已知两边求角及其三角函数 已知一边一角求另一边 已知一边一角求另一边
2、特殊角的三角函数值
三角函数
角α
sinα
cos α
tan α
300
450
600
坡角:坡面与水平面的夹角.
坡度越大,坡面越陡。
坡度i(坡比):
工程术语
i=3:5
等于坡角的正切.
1.在Rt△ABC中,各边都扩大5倍,则角A的三角函数值( )
A.不变 B.扩大5倍
C.缩小5倍 D.不能确定
A
2、Rt⊿ABC 中,∠C=90°, ∠B =60°,
AB=4,则AC= ,BC= ,
sinA= cosA= tanA= 。
2
3.Rt△ABC中,∠ACB = 90°,
CD⊥AB 于D,AC=5,AB=6,则
sin∠1= .
4.Rt△ABC中,∠ACB = 90°,CD
是AB边上的中线,若AC=5,AB=6,
则sin∠1= 。
1
5.如图,沿AC方向开山修路,为加快施工进度,要在山的另一边同时施工,现在从AC上取一点B,使 ∠ ABD=140°,BD=500米,∠D=50°,要使A、C、E在一条直线上,那么点E、D间的距离应为( )
B
B、500cos50°米
A.500sin50°米
C.500tan50°米
6.某地夏季中午,当太阳移到屋顶上方偏东时,光线与地面成α角,房屋朝南的窗子高AB=h米,要在窗子外面上方安装一个水平挡光板AC,使午间光线不能直接射人室内如图1-1-18,那么挡光板AC的宽度为=_____.
锐角三角形????
直角三角形
钝角三角形?
等腰三角形
8.如图铁路路基横断面为一个等腰梯形, 若腰的坡度为2:3,顶宽为3米,路基高为4米,则路基的下底宽是____
坡度
A
A.15米 B.12米
C.9米 D.7米
如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸取两点B、C,测得∠ABC = 45°,∠ACB = 31°,量得BC长为20米。求小河的宽度。(参考数值:tan31°≈ ,sin31°≈ )
20
45°
31°
如图,为测量小河的宽度,先在河岸边任取一点A,再在河的另一岸取两点B、C,测得∠ABM= 45°,∠ACB = 31°,量得BC长为20米。求小河的宽度。(参考数值:tan31°≈ ,sin31°≈ )
45°
31°
20
变式练习1
45°
31°
20
5
变式练习2
45°
31°
20
5
一题多解
(2)精确值(有效数字,保留数位、提供的参考值)
(6分)
(1)转化成基本模型
1、某商场准备改善原有楼梯的安全性能,把倾斜角由原来的40?减至35?.已知原楼梯AB长为5m,调整后的楼梯所占地面CD有多长?
参考数据:
sin40?≈0.64,
cos40?≈0.77,
sin35?≈0.57,
tan35?≈0.70)
(结果精确到0.1m)
B
37°
48°
D
C
A
第19题图
2、小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为37°,大厦底部B的俯角为48°.求小明家所在居民楼与大厦的距离CD的长度.
参考数据:
(结果保留整数)
E
本节课学习了哪些知识?
领悟到哪些解决问题的方法?
学习体会
祝同学们
学习进步!
