青岛版数学六三制五年级上册第4单元知识点及典型题目训练一(含解析)
文档属性
| 名称 | 青岛版数学六三制五年级上册第4单元知识点及典型题目训练一(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 496.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-24 09:02:36 | ||
图片预览



文档简介
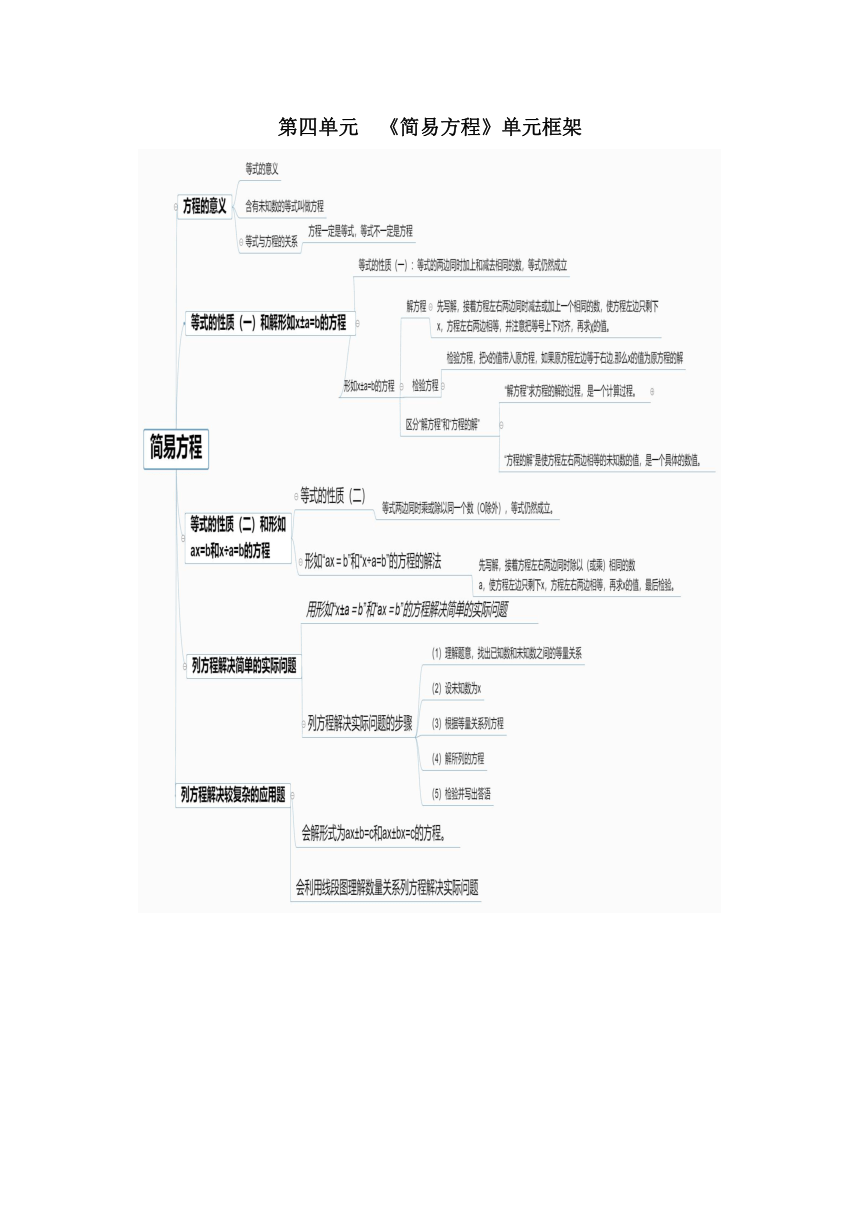
第四单元 《简易方程》单元框架
信息窗1——方程的意义
一、知识点解读
1.等式的意义(理解识记)
知识点:把相等的量、式子或数用等号连接起来就形成了等式。
教学要求:等式是方程概念的生长点,认识方程需要先理解等式,学习时可以把天平两边平衡的现象抽象成等式,可以借助直观情境体会等式的含义。
2.方程的意义(理解识记)
知识点:含有未知数的等式叫做方程。
教学要求:根据知识点1等式的意义由天平平衡写出含有未知数的等式,进而引出方程的教学,这样设计,主要是给学生创造一个用眼观察,用脑思考的机会,让他们亲自感知多个含有未知数的等式的来源,将“重视结论”的教学转变为“重视过程”的教学,不生硬的塞给学生现成的结论,让学生充分经历方程意义的生成过程。教学时要让学生明白“含有未知数”和“等式”是方程的两个显著特征。
3.等式与方程的关系(理解识记)
知识点:方程一定是等式,但等式不一定是方程。两者之间的关系可以用下图表示:
教学要求:在完成知识点1和2的教学后,紧接着让学生自己对比两者的异同点,总结方程与等式的关系。
二、知识拓展
用方程表示简单的数量关系。
通过看图列方程,让学生经历观察、思考和整理的过程,理清并正确表述图中各数量之间的等量关系,写出正确的方程表达式。
三、知识点训练
基础训练
填一填。
①含有( )的( )叫方程。
②一块长方形花坛的面积是120平方米,长χ米,宽( )米。
③三年级植树68棵,六年级比三年级多植χ棵,那么68 + χ表示( )。
2. 下列哪些是等式,是等式的画“√”
5 + 6 = 11( ) 13 + 8 < 30 ( ) 6y - 7 ( )
3. 下列哪些是方程,是方程的画“√”
2.5 × 4 = 10 ( ) 34 ÷ y = 3( ) 5m = 0 ( )
能力提升
用方程表示下面的等量关系。
①的6倍等于9.6。
②减去1.8的差是5.1。
根据题中的数量关系列出方程。
①
②
根据图意先找出题中的等量关系,然后再列方程。
小兵共根绳子,借出45根,还剩10根。
①跳绳的根数-( )=还剩的?
方程:
?? ②( )-还剩的=借出的
方程:
拓展应用
1. 看图列方程。
2.
训练题参考答案及解析
基础训练
① 未知数、等式 ② 120 ÷ χ ③ 六年级植树棵树
(√)( )( )
( )(√)(√)
能力提升
① 6 = 9.6 ② - 1.8 = 5.1
① 4 = 184 ② + 2.5 = 4.6
① 跳绳的根数-(借出的根数)=还剩的? - 45 = 10
②(跳绳的根数 )-还剩的=借出的 - 10 = 45
拓展应用
解析:教师先提出看图要求:一、从图中你可以看出那些数学信息?二、这些数学信息之间存在什么等量关系?学生经过独立思考、交流研讨得出:题中“练习本的价钱 + 钢笔的价钱= 4.8元,列出方程 + 5 = 4.8。
题中数量关系为“已看的页数+剩下的页数=总页数”,列出方程4a + 24 = 96。
信息窗2——等式的性质(一)和解形如χa=b的方程
一、知识点解读
1.等式的性质(一)(理解识记)
知识点:等式的两边同时加上或减去同一个数,等式仍然成立。
教学要求:该知识点采用体验探究的教学方式,首先由老师演示天平实验,分别在天平两侧放上和拿掉同一质量的物体天平仍保持平衡,通过天平反复验证,得出:在天平的两边同时加上或减去相同重量的物体,天平还是平衡的。并把实验转化为数学问题并列出数学式子;再让学生根据所列的式子,提出问题:通过天平实验所得到的式子你能联想到等式有什么性质?由学生独立思考归纳出等式的性质(一),然后再把等式的性质抽象为数学的符号语言并表示出来,即“等式两边同时加上或减去同一个数,等式仍然成立”。
2.形如χa=b的方程的解法(掌握运用)
知识点:解法:先写解,接着方程左右两边同时减去或加上一个相同的数,使方程左边只剩下χ,方程左右两边相等,并注意把等号上下对齐,再求χ的值。
检验方程,把χ的值带入原方程,如果原方程左边等于右边,那么χ的值为原方程的解;如果原方程左边不等于右边,那么χ的值不是原方程的解。
教学要求:让学生在理解了等式的性质(一)的基础上小组合作独立探究形如χa=b的方程的解法,最后加以总结,并引导学生进行验算,教师出示规范的检验过程,培养学生养成检验的好习惯,力求计算准确。
3.区分“方程的解”和“解方程”这两个概念。
知识点:“解方程”求方程的解的过程,是一个计算过程。
“方程的解”是使方程左右两边相等的未知数的值,是一个具体的数值。
教学要求:掌握了检验方程的方法教师顺其自然的引出方程的解和解方程的意义,并让学生思考归纳总结方程的解和解方程的意义有何不同?(知道“方程的解”是一个结果,“解方程”是一个过程。)
二、知识拓展
根据图中的数量关系列方程解决生活中的实际问题。
根据数量关系列方程,也是通过寻找实际问题中数量之间的相等关系(等量关系),列出含有未知数的等式(方程)。这是解决实际问题的一种重要方法。首先看图弄清题意,分清已知与所求,找准各种数量之间的等量关系,再列方程并利用等式性质(一)正确解答。
三、知识点训练
基础训练
判断。
(1)方程的解就是解方程。 ( )
(2)当χ = 2时,4χ比7多1。 ( )
(3)χ = 9是方程χ - 1 = 8的解。 ( )
(4)解方程:12 + χ = 18.5 = 18.5 - 12 = 16.5。 ( )
(5)等式的左右两边同时加上或减去相同的数,等式仍然成立。( )
2. 在○里填运算符号,在□里填数字。
χ - 20 = 30 3.6 + χ = 5.7
解: χ - 20 ○ □ = 30 ○ □? 解:3.6 + χ ○ □ = 5.7○□
χ = □ χ = □
3. 你知道( )里哪个χ的值是方程的解吗?圈一圈。
(1)χ + 24 = 36 ( χ = 60, χ = 12 )
(2)χ - 37 = 56 ( χ = 19, χ = 93 )
(3)χ + 7.9 = 18.4 ( χ = 10.5, χ = 26.3 )
(4) χ - 35.2 = 47.9 (χ = 12.7, χ = 83.1 )
能力提升
解方程(带“★”写出检验过程)。
Χ + 659 = 1005 χ + 3 = 15 ★13 + χ = 28.5
写出下列各题的等量关系并列方程。
①河中原有16只小鸭,上岸χ只,河中还剩下9只小鸭。。
等量关系 :
方程:
②长方形的长χ厘米,宽5厘米,周长67厘米。
等量关系 :
方程:
③果园里有桃树126棵,梨树有χ棵,桃树和梨树共有768棵。
等量关系 :
方程:
某野生动物园的动物共计208种,其中国家一、二级保护动物共116种,一级保护动物有54种。二级保护动物有多少种?(列方程解答)
拓展应用
1. 看图列方程,并求出方程的解
①
②
爸爸的体重是82千克,妈妈的体重比爸爸的少30千克,比小明的多12.5千克,小明的体重是多少千克?
训练题参考答案及解析
基础训练
(1) × (2) √ (3) √ (4) × (5) √
2. χ - 20 = 30 3.6 + χ = 5.7
解:χ - 20 + 20 = 30 + 20? 解: 3.6 + χ - 3.6 = 5.7 - 3.6
χ = 50 χ = 2.1
(1) χ = 12 (2) χ = 93 (3) χ = 10.5 (4) χ = 83.1
能力提升
1、 χ + 659 = 1005
解:χ + 659 - 659 = 1005 - 659
x = 346
χ + 3 = 15
解:χ + 3 - 3 = 15 - 3
x = 12
★ 13 + χ = 28.5 检验:方程左边 = 13 + χ
解:13 + χ - 13 = 28.5 - 13 = 13 + 15.5
χ = 15.5 = 28.5
= 方程右边
所以,χ = 15.5是方程13 + χ = 28.5的解。
①等量关系 :河中原有的只数-上岸的只数=剩下的只数 方程:16 - χ = 9
②等量关系 :(长+宽)×2=长方形的周长; 方程:(χ+5)×2 = 67
③等量关系 :桃树的棵数+梨树的棵数=总棵树;方程:126 + χ = 768
3. 解:设二级保护动物有χ种。
54 + χ = 116
54 + χ - 54 = 116 - 54
χ = 62
答:二级保护动物有62种。
拓展应用
解析:看图寻找数量之间的等量关系,是学习列方程解应用题的关键。
图①数量之间的等量关系:4个冰激凌的价钱+1个汉堡的价钱=19.9元,由此列方程: 2.5 × 4 + χ = 19.9
解:10 + χ = 19.9
10 + χ - 10 = 19.9 - 10
χ = 9.9
图②数量之间的等量关系:男孩的身高+21厘米=大人的身高
由此列方程: 21 + χ = 175
解: 21 + χ - 21 = 175 - 21
χ = 154
思路分析:本题关键是应弄清数量关系,妈妈的体重=爸爸的体重-30千克 小明的体重+12.5千克=妈妈的体重,两个关系式合二为一,等号两侧都用来表示妈妈的体重,即:小明的体重+12.5千克=爸爸的体重-30千克,然后依据数量关系式设未知数列方程解答即可。
解:设小明的体重为χ千克
χ + 12.5 = 82 - 30
χ + 12.5 - 12.5 = 52 - 12.5
χ = 39.5
答:小明的体重为39.5千克。
信息窗1——方程的意义
一、知识点解读
1.等式的意义(理解识记)
知识点:把相等的量、式子或数用等号连接起来就形成了等式。
教学要求:等式是方程概念的生长点,认识方程需要先理解等式,学习时可以把天平两边平衡的现象抽象成等式,可以借助直观情境体会等式的含义。
2.方程的意义(理解识记)
知识点:含有未知数的等式叫做方程。
教学要求:根据知识点1等式的意义由天平平衡写出含有未知数的等式,进而引出方程的教学,这样设计,主要是给学生创造一个用眼观察,用脑思考的机会,让他们亲自感知多个含有未知数的等式的来源,将“重视结论”的教学转变为“重视过程”的教学,不生硬的塞给学生现成的结论,让学生充分经历方程意义的生成过程。教学时要让学生明白“含有未知数”和“等式”是方程的两个显著特征。
3.等式与方程的关系(理解识记)
知识点:方程一定是等式,但等式不一定是方程。两者之间的关系可以用下图表示:
教学要求:在完成知识点1和2的教学后,紧接着让学生自己对比两者的异同点,总结方程与等式的关系。
二、知识拓展
用方程表示简单的数量关系。
通过看图列方程,让学生经历观察、思考和整理的过程,理清并正确表述图中各数量之间的等量关系,写出正确的方程表达式。
三、知识点训练
基础训练
填一填。
①含有( )的( )叫方程。
②一块长方形花坛的面积是120平方米,长χ米,宽( )米。
③三年级植树68棵,六年级比三年级多植χ棵,那么68 + χ表示( )。
2. 下列哪些是等式,是等式的画“√”
5 + 6 = 11( ) 13 + 8 < 30 ( ) 6y - 7 ( )
3. 下列哪些是方程,是方程的画“√”
2.5 × 4 = 10 ( ) 34 ÷ y = 3( ) 5m = 0 ( )
能力提升
用方程表示下面的等量关系。
①的6倍等于9.6。
②减去1.8的差是5.1。
根据题中的数量关系列出方程。
①
②
根据图意先找出题中的等量关系,然后再列方程。
小兵共根绳子,借出45根,还剩10根。
①跳绳的根数-( )=还剩的?
方程:
?? ②( )-还剩的=借出的
方程:
拓展应用
1. 看图列方程。
2.
训练题参考答案及解析
基础训练
① 未知数、等式 ② 120 ÷ χ ③ 六年级植树棵树
(√)( )( )
( )(√)(√)
能力提升
① 6 = 9.6 ② - 1.8 = 5.1
① 4 = 184 ② + 2.5 = 4.6
① 跳绳的根数-(借出的根数)=还剩的? - 45 = 10
②(跳绳的根数 )-还剩的=借出的 - 10 = 45
拓展应用
解析:教师先提出看图要求:一、从图中你可以看出那些数学信息?二、这些数学信息之间存在什么等量关系?学生经过独立思考、交流研讨得出:题中“练习本的价钱 + 钢笔的价钱= 4.8元,列出方程 + 5 = 4.8。
题中数量关系为“已看的页数+剩下的页数=总页数”,列出方程4a + 24 = 96。
信息窗2——等式的性质(一)和解形如χa=b的方程
一、知识点解读
1.等式的性质(一)(理解识记)
知识点:等式的两边同时加上或减去同一个数,等式仍然成立。
教学要求:该知识点采用体验探究的教学方式,首先由老师演示天平实验,分别在天平两侧放上和拿掉同一质量的物体天平仍保持平衡,通过天平反复验证,得出:在天平的两边同时加上或减去相同重量的物体,天平还是平衡的。并把实验转化为数学问题并列出数学式子;再让学生根据所列的式子,提出问题:通过天平实验所得到的式子你能联想到等式有什么性质?由学生独立思考归纳出等式的性质(一),然后再把等式的性质抽象为数学的符号语言并表示出来,即“等式两边同时加上或减去同一个数,等式仍然成立”。
2.形如χa=b的方程的解法(掌握运用)
知识点:解法:先写解,接着方程左右两边同时减去或加上一个相同的数,使方程左边只剩下χ,方程左右两边相等,并注意把等号上下对齐,再求χ的值。
检验方程,把χ的值带入原方程,如果原方程左边等于右边,那么χ的值为原方程的解;如果原方程左边不等于右边,那么χ的值不是原方程的解。
教学要求:让学生在理解了等式的性质(一)的基础上小组合作独立探究形如χa=b的方程的解法,最后加以总结,并引导学生进行验算,教师出示规范的检验过程,培养学生养成检验的好习惯,力求计算准确。
3.区分“方程的解”和“解方程”这两个概念。
知识点:“解方程”求方程的解的过程,是一个计算过程。
“方程的解”是使方程左右两边相等的未知数的值,是一个具体的数值。
教学要求:掌握了检验方程的方法教师顺其自然的引出方程的解和解方程的意义,并让学生思考归纳总结方程的解和解方程的意义有何不同?(知道“方程的解”是一个结果,“解方程”是一个过程。)
二、知识拓展
根据图中的数量关系列方程解决生活中的实际问题。
根据数量关系列方程,也是通过寻找实际问题中数量之间的相等关系(等量关系),列出含有未知数的等式(方程)。这是解决实际问题的一种重要方法。首先看图弄清题意,分清已知与所求,找准各种数量之间的等量关系,再列方程并利用等式性质(一)正确解答。
三、知识点训练
基础训练
判断。
(1)方程的解就是解方程。 ( )
(2)当χ = 2时,4χ比7多1。 ( )
(3)χ = 9是方程χ - 1 = 8的解。 ( )
(4)解方程:12 + χ = 18.5 = 18.5 - 12 = 16.5。 ( )
(5)等式的左右两边同时加上或减去相同的数,等式仍然成立。( )
2. 在○里填运算符号,在□里填数字。
χ - 20 = 30 3.6 + χ = 5.7
解: χ - 20 ○ □ = 30 ○ □? 解:3.6 + χ ○ □ = 5.7○□
χ = □ χ = □
3. 你知道( )里哪个χ的值是方程的解吗?圈一圈。
(1)χ + 24 = 36 ( χ = 60, χ = 12 )
(2)χ - 37 = 56 ( χ = 19, χ = 93 )
(3)χ + 7.9 = 18.4 ( χ = 10.5, χ = 26.3 )
(4) χ - 35.2 = 47.9 (χ = 12.7, χ = 83.1 )
能力提升
解方程(带“★”写出检验过程)。
Χ + 659 = 1005 χ + 3 = 15 ★13 + χ = 28.5
写出下列各题的等量关系并列方程。
①河中原有16只小鸭,上岸χ只,河中还剩下9只小鸭。。
等量关系 :
方程:
②长方形的长χ厘米,宽5厘米,周长67厘米。
等量关系 :
方程:
③果园里有桃树126棵,梨树有χ棵,桃树和梨树共有768棵。
等量关系 :
方程:
某野生动物园的动物共计208种,其中国家一、二级保护动物共116种,一级保护动物有54种。二级保护动物有多少种?(列方程解答)
拓展应用
1. 看图列方程,并求出方程的解
①
②
爸爸的体重是82千克,妈妈的体重比爸爸的少30千克,比小明的多12.5千克,小明的体重是多少千克?
训练题参考答案及解析
基础训练
(1) × (2) √ (3) √ (4) × (5) √
2. χ - 20 = 30 3.6 + χ = 5.7
解:χ - 20 + 20 = 30 + 20? 解: 3.6 + χ - 3.6 = 5.7 - 3.6
χ = 50 χ = 2.1
(1) χ = 12 (2) χ = 93 (3) χ = 10.5 (4) χ = 83.1
能力提升
1、 χ + 659 = 1005
解:χ + 659 - 659 = 1005 - 659
x = 346
χ + 3 = 15
解:χ + 3 - 3 = 15 - 3
x = 12
★ 13 + χ = 28.5 检验:方程左边 = 13 + χ
解:13 + χ - 13 = 28.5 - 13 = 13 + 15.5
χ = 15.5 = 28.5
= 方程右边
所以,χ = 15.5是方程13 + χ = 28.5的解。
①等量关系 :河中原有的只数-上岸的只数=剩下的只数 方程:16 - χ = 9
②等量关系 :(长+宽)×2=长方形的周长; 方程:(χ+5)×2 = 67
③等量关系 :桃树的棵数+梨树的棵数=总棵树;方程:126 + χ = 768
3. 解:设二级保护动物有χ种。
54 + χ = 116
54 + χ - 54 = 116 - 54
χ = 62
答:二级保护动物有62种。
拓展应用
解析:看图寻找数量之间的等量关系,是学习列方程解应用题的关键。
图①数量之间的等量关系:4个冰激凌的价钱+1个汉堡的价钱=19.9元,由此列方程: 2.5 × 4 + χ = 19.9
解:10 + χ = 19.9
10 + χ - 10 = 19.9 - 10
χ = 9.9
图②数量之间的等量关系:男孩的身高+21厘米=大人的身高
由此列方程: 21 + χ = 175
解: 21 + χ - 21 = 175 - 21
χ = 154
思路分析:本题关键是应弄清数量关系,妈妈的体重=爸爸的体重-30千克 小明的体重+12.5千克=妈妈的体重,两个关系式合二为一,等号两侧都用来表示妈妈的体重,即:小明的体重+12.5千克=爸爸的体重-30千克,然后依据数量关系式设未知数列方程解答即可。
解:设小明的体重为χ千克
χ + 12.5 = 82 - 30
χ + 12.5 - 12.5 = 52 - 12.5
χ = 39.5
答:小明的体重为39.5千克。
