青岛版数学六三制五年级上册第4单元知识点及典型题目训练二(含解析)
文档属性
| 名称 | 青岛版数学六三制五年级上册第4单元知识点及典型题目训练二(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 539.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-24 00:00:00 | ||
图片预览





文档简介
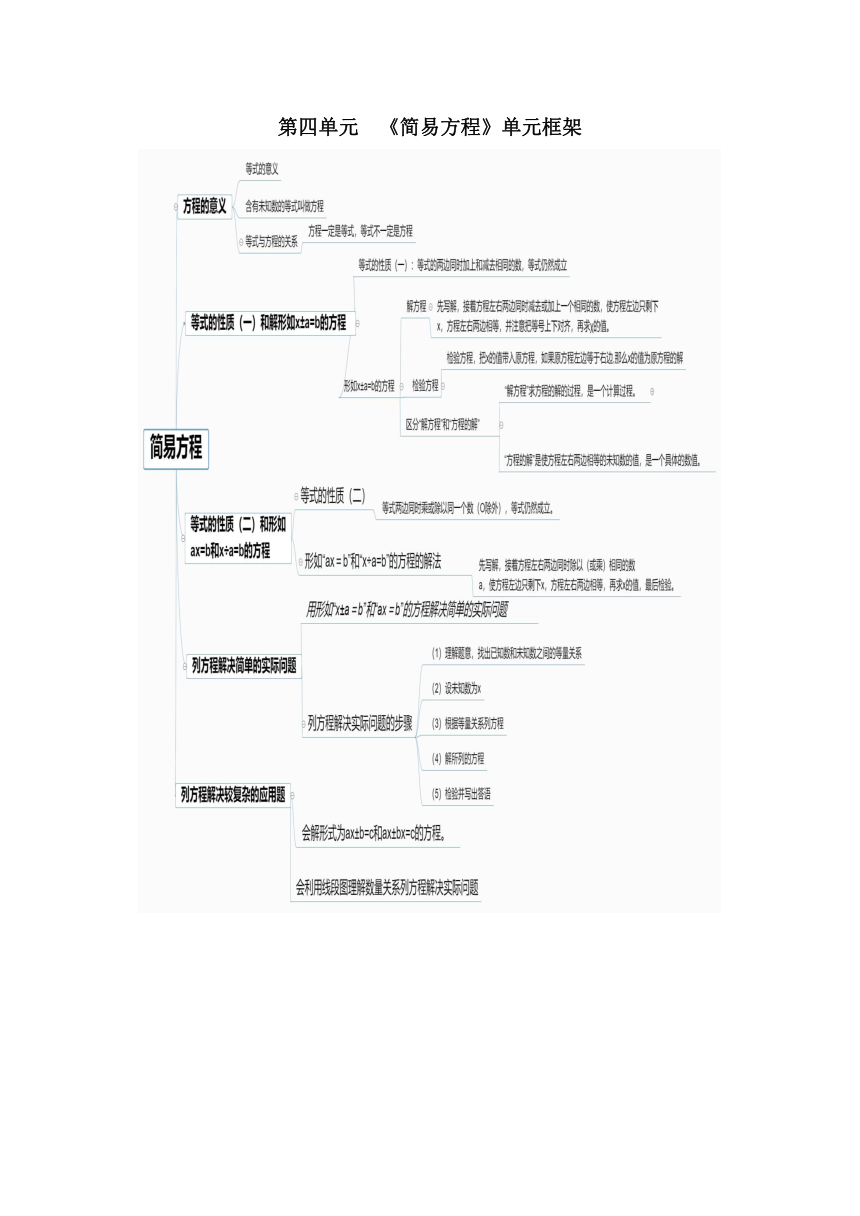
第四单元 《简易方程》单元框架
信息窗3——等式的性质(二)和解形如aχ=b和χ÷a=b的方程
一、知识点解读
1.等式的性质(二)(理解识记)
知识点:等式两边同时乘或除以同一个数(O除外),等式仍然成立。
教学要求:教学时要充分运用学生在信息窗2中积累的探索等式性质的活动经验,通过天平平衡的原理放手让学生自主去尝试、去探索等式的性质(二)(在自主学习与合作交流中,如果学生没有想到同时除以0,教师可以自己向学生提出问题,简单讨论后,很快想到除法中除数不能为0,因而得出同时除以一个不为0的数的范围。)
2.运用等式的性质(二)解形如“aχ=b”和“χ÷a=b”的方程(掌握运用)
知识点:解法:先写解,接着方程左右两边同时除以(或乘)相同的数a,使方程左边只剩下χ,方程左右两边相等,再求χ的值,最后检验。
教学要求:让学生在理解了等式的性质(一)的基础上独立探究形如“aχ=b”和 “χ÷a=b”方程的解法,最后加以总结,并引导学生进行验算,培养学生自觉检验的意识,力求计算准确。
二、知识拓展
根据题目中的数量关系列方程解决生活中的实际问题。
根据数量关系列方程,也是通过寻找实际问题中数量之间的相等关系(等量关系),列出含有未知数的等式(方程)。这是解决实际问题的一种重要方法。首先看图弄清题意,分清已知与所求,找准各种数量之间的等量关系,再列方程并利用等式性质(二)正确解答。
常见的数量式、计算公式等都可以作为等量关系列方程。例如:
速度×时间=路程 工作效率×时间=工作总量 单价×数量=总价
(长+宽)×2=长方形的周长 长×宽=长方形的面积
边长×4=正方形的周长 边长×边长=正方形的面积
三、知识点训练
基础训练
在○里运算符号,在□里填数字。
1.5χ = 12 χ ÷ 3.2 = 17
解: 1.5χ ○ □ = 12 ○ □? 解: χ ÷ 3.2 ○ □ = 17 ○ □
χ = □? χ = □
2. 把方程与它对应的解用线连起来。
6χ = 0 χ = 2
χ ÷ 2 = 1 χ = 0.5
2χ = 1 χ = 0
3. 解方程。(带“★”写出检验过程)
2.5χ = 7.5 23χ = 138 ★ χ ÷ 4 = 25.5
能力提升
看图列方程并解答。
①
②
一块正方形菜地周长是64米,正方形的边长是多少米?
3. 黄豆长成豆芽后的质量是原来质量的8.5倍,现在需要豆芽493千克,需要黄豆多少千克?
拓展应用
三个连续自然数的和是54,求这三个数分别是多少?
2. 信业商厦为了方便残疾人的轮椅通行,做了一项关于建筑物高度的规定:每1米高的斜坡,至少需要12米的水平长度。商厦前面的空地长18米,那么此处斜坡最高是多少米?
训练题参考答案及解析
基础训练
1.5χ = 12 χ ÷ 3.2 = 17
解: 1.5χ ÷ 1.5 = 12 ÷ 1.5? 解: χ ÷ 3.2 × 3.2 = 17×3.2
χ = 8 χ = 54.4
2. 6χ = 0 χ = 2
χ ÷ 2 = 1 χ = 0.5
2χ = 1 χ = 0
2.5χ = 7.5 23χ = 138
解:2.5χ ÷ 2.5 = 7.5 ÷ 2.5 解:23χ ÷ 23 = 138 ÷ 23
x = 3 χ = 6
★ χ ÷ 4 = 25.5 检验: 方程左边 = χ ÷ 4
解:χ ÷ 4 × 4 = 25.5 × 4 = 102 ÷ 4
χ = 102 = 25.5
= 方程右边
所以,χ = 102是方程χ ÷ 4 = 25.5的解。
能力提升
1. 3y = 189 4χ = 24
解:3y ÷ 3 = 189 ÷ 3 解: 4χ ÷ 4 = 24 ÷ 4
y = 63 χ = 6
2. 解:设正方形菜地的边长是χ米。
4χ = 64
4χ ÷ 4 = 64 ÷ 4
χ = 16
答:正方形菜地的边长是16米。
3. 解:设需要黄豆χ千克。
8.5χ = 493
8.5χ ÷ 8.5 = 493 ÷ 8.5
χ = 58
答:需要黄豆58千克。
拓展应用
思路分析:三个连续自然数按从小到大的顺序排列,应该是后一个数比前一个数大1。可以设其中一个数为χ,另外两个数都可以用含有χ的式子表示,这样就可以根据三个数的和是54这一等量关系列方程。
方法一:
解:设这三个连续自然数中,最小的数为χ,则中间的数为χ+1,最大的数为χ+2。
χ + χ + 1 + χ + 2 = 54
χ = 17
χ + 1 = 17 + 1 = 18 χ + 2= 17 + 2 = 19
方法二:
解:设这三个连续自然数中,中间的数为χ,则最小的数为χ - 1,最大的数为χ + 1。
χ - 1 + χ + χ + 1 = 54
χ = 18
χ - 1 = 18 - 1 = 17 χ + 1 = 18 + 1 = 19
方法三:
解:设这三个连续自然数中,最大的数为χ,则中间的数为χ-1,最小的数为χ-2。
χ - 2 + χ - 1 + χ = 54
χ = 19
χ - 2 = 19 - 2 = 17 χ - 1 = 19 - 1 = 18
答:这三个连续自然数分别是17、18、19。
思路分析:1米高的斜坡至少需要12米的水平长度,由此得出题中的等量关系式是“12×斜坡高度=水平长度”。根据等量关系设此处斜坡最高是χ米,列方程求解。
解:设此处斜坡最高是χ米。
12χ = 18
12χ ÷ 12 = 18 ÷ 12
χ = 1.5
答:此处斜坡高度最高是1.5米。
信息窗4——列方程解决简单的实际问题
一、知识点解读
用形如“χ±a=b”和“aχ=b”的方程解决简单的实际问题(掌握运用)
知识点:列方程解决实际问题的步骤:
理解题意,找出已知数和未知数之间的等量关系
设未知数为χ
根据等量关系列方程
解所列的方程
检验并写出答语
教学要求:教学时,教师可以先引导学生分析要想解决问题需要弄清楚数量关系,让学生在独立思考的基础上展开讨论。学生可能出现两种情况:一种是用算术法解决,另一种是用方程解决。这时,教师要引导学生用列方程的方法解决问题,分析数量间的相等关系,写出等量关系式,再启发学生根据等量关系列出方程并解答。求出方程的解后,教师要启动教材中的问题“你会检验吗”,提醒学生把算得的结果代到原题当中去检验。
二、知识拓展
1.列方程解决问题时,要体现用方程解题的意义
例如:世界第一长河尼罗河全长约6671千米,比中国第一长河长江约长371千米,长江全长约多少千米?
错误示例:解:设长江全长约千米。
=6671-371
=6300
答:长江全长约6300千米。
正确解答:解:设长江全长约千米。
+ 371 = 6671
+ 371 - 371 = 6671 - 371
= 6300
答:长江全长约6300千米。
错解中计算并无错误,但没有体现用方程解题的意义,列出的方程中未知数并没有参与运算,本质上还是由已知量推出未知量,是一种算术法。列方程解决问题时,通常不能把未知数放在等号一边,而是用代替等量关系中的未知量直接列出方程。体验用方程解答应用题的优势,从而更加热爱数学,热爱生活。
2. 列方程解决实际问题时,方程的解的后面不写单位名称。
方程是一种等式,方程两边无论是数还是量都是相等的,因此两边的单位名称可同时约去。求方程的解的过程就成了数的恒等变形的过程,最后的结果是没有单位名称的,只需要在答语中把单位名称写清楚就行。
三、知识点训练
基础训练
看图写出等量关系式,并列出方程.
等量关系式:
方程:
2. 看图列方程并求出方程的解。
3. 小明去买商店衣服,优惠了38元,现价是75元,原价多少钱?(写出等量关系式并列方程解答)
等量关系式:
能力提升
天安门广场是世界上最大的首都中心广场,广场占地面积44万平方米,比俄罗斯红场多34.9万平方米。俄罗斯红场占地面积是多少万平方米?
树林中有杨树270棵,杨树的棵数是柳树的5倍。树林中杨树和柳树共有多少棵?
一块边长10米的正方形菜地与一块长12.5米的长方形菜地的面积相等,长方形菜地的宽是多少米?
拓展应用
远望巍巍塔七层,红红点点倍加增,共计三百八十一,试问顶层几盏灯?
7年前爸爸的岁数是小华的3倍,7年后是小华的2倍,小华今年多少岁?
训练题参考答案及解析
基础训练
1. 上衣的价钱+裙子的价钱=总价钱
χ + 46 = 112
2. 4χ = 60 120 + χ = 165
解:4χ ÷ 4 = 60 ÷ 4 解: 120 + χ - 120 = 165 - 120
χ = 15 χ = 45
原来的价钱 - 优惠的价钱 = 现在的价钱
解:设原价χ元。
χ - 38 = 75
χ - 38 + 38 = 75 + 38
χ = 113
答:原价113元。
能力提升
解:设俄罗斯红场占地面积是χ万平方米。
χ + 34.9 = 44
χ + 34.9 - 34.9 = 44 - 34.9
χ = 9.1
答:俄罗斯红场占地面积是9.1万平方米。
2. 解:设柳树有χ棵。
5χ = 270
χ = 54
270 + 54 = 324(棵)
答:树林中杨树和柳树共有324棵。
3. 解:设长方形菜地的宽是χ米.
12.5χ = 10 × 10
12.5χ ÷ 12.5 = 10 × 10 ÷ 12.5
χ = 8
答:长方形菜地的宽是8米。
拓展应用
思路分析:宝塔共7层,每层都挂着红灯,红灯的总数是381盏,红灯从顶层到底层“倍加增”,也就是每相邻的下一层红灯盏数都是上一层的2倍。可以设灯塔的顶层有χ盏灯,则第6层有2χ盏灯,第5层有4χ盏灯,依此类推,再根据红灯的总盏数列出方程。
解:设塔的顶层有χ盏灯。
χ + 2χ + 4χ + 8χ + 16χ + 32χ + 64χ = 381
127χ = 381
χ = 3
答:塔的顶层有3盏红灯。
2. 思路分析:本题直接设小华今年的年龄为χ岁,列方程、解方程都比较困难,可以设小华7年前是χ岁,则爸爸7年前为3χ岁。题中的等量关系比较隐蔽,就是:7年前爸爸的年龄 + 7 + 7 = 7年后爸爸的年龄,用含有χ的代数式表示出爸爸7年前、7年后的年龄,根据上面的等量关系,可以列出方程:
解:设小华7年前χ岁,则爸爸7年前为3χ岁。
3χ + 7 + 7 = 2(χ + 7 + 7)
3χ + 14 = 2χ + 28
? χ = 14
所以小华今年的年龄为:?14 + 7 = 21(岁)
答:小华今年21岁。
信息窗5——列方程解较复杂的应用题
一、知识点解读
1.学会解形式复杂的方程。(掌握运用)
知识点:学会解形式为aχ±b=c和aχ±bχ=c的方程。
教学要求:解形式为aχ±b=c和aχ±bχ=c的方程,先让学生主动去尝试解答,然后在交流研讨中会发现,解形式为aχ±b=c的方程,先运用了等式性质(一),又运用了等式性质(二)。解形式为aχ±bχ=c的方程,是运用四年级上册《用字母表示数》中的计算,如:7χ+8χ=15χ,把 aχ±bχ=c转化为(a±b)χ=c的简单方程。
2.会利用线段图理解数量关系列方程解决实际问题。(掌握运用)
知识点:学会看线段图理解数量关系列方程解决实际问题,在此基础上会画线段图。
教学要求:文字信息比较抽象,不直观,学生思维比较困难,教学时教师可以运用多媒体辅助教学,通过课件展示线段图的画法、动态演示数量关系的推理过程,呈现两种思路的对比分析,从而帮助学生学会分析、判断、推理数量关系,理清解题思路,用方程解决实际问题,感受画图解决问题的策略价值,从而让学生学会看图的方法。然后通过巩固练习,让学生体验运用画图策略解决问题的方便,并通过线段图说一说数量关系,提高学生分析问题、解决问题的能力。
二、知识拓展
船在江河里航行时,除了本身的前进速度外,还受到流水的推送或顶逆,在这种情况下计算船只的航行速度、时间和所行的路程,叫做流水行船问题。流水行船问题,是行程问题中的一种。
流水行船问题有以下两个基本公式,
顺水速度=船速+水速
逆水速度=船速-水速
船速是指船本身的速度,也就是静水中单位时间所走的路程。
水速,是指水在单位时间里流过的路程。
顺水速度和逆水速度分别指顺流航行时和逆流航行时船在单位时间里所行的路程。
三、知识点训练
基础训练
看图写出等量关系式,并列出方程。
等量关系式:
方程:
解方程:
5χ + 15 = 120 3.8χ - χ = 0.56 χ - 0.85χ = 3
写出题中的等量关系列出方程并求出方程的解。
一个水果店有苹果χ千克,香蕉122千克。香蕉的质量比苹果的3倍少28千克。
能力提升
解方程。
7χ + 3χ + 26 = 74 9χ + 8 = 102 - 13
一个长方形池塘的周长是300米。它的长是100米,宽是多少米?
一副乒乓球拍的价钱比一副羽毛球拍贵19元;乒乓球拍的价钱是羽毛球拍的1.5倍。一副乒乓球拍多少元钱?
拓展应用
一条轮船在两码头间航行,顺水航行需要4小时,逆水航行需5小时,水速是每小时5千米,这条船在静水中每小时行多少千米?
2. 一群娃娃去赶集,集上买了一堆梨,一人一个多一个,一人两个少两个,请问君子知道否,几个娃娃几个梨?
训练题参考答案及解析
基础知识
苹果的个数+梨的个数=总个数 χ + 2χ = 93
5χ + 15 = 120
解: 5χ+ 15 — 15 = 120 - 15
5χ = 105
χ = 21
3.8χ - χ = 0.56
解: 2.8χ = 0.56
2.8χ÷2.8 = 0.56 ÷ 2.8
χ = 0.2
χ - 0.85χ = 3
解: 0.15χ = 3
0.15χ ÷ 0.15 = 3 ÷ 0.15
χ = 20
3. 苹果重量×3-少的千克数=香蕉的重量
3χ - 28 = 122
解: 3χ - 28 + 28 = 122+28
3χ = 150
χ = 50
答:苹果有50千克。
能力提升
7χ + 3χ + 26 = 74
解: 10χ + 26 = 74
χ = 4.8
9χ + 8 = 102 - 13
解: 9χ + 8 = 89
χ = 9
2. 思路分析:已知长方形的周长和长求宽可以直接套用长方形周长公式:长方形的周长=(长+宽)×2
解:设宽是χ米。
(100 + χ )× 2 = 300
(100+χ)× 2 ÷ 2 = 300 ÷ 2
100 + χ = 150
100 + χ - 100 = 150 - 100
χ = 50
答:宽是50米。
3. 解:设一副羽毛球拍χ元,那么一副乒乓球拍1.5χ元。
1.5χ - χ = 19
0.5χ = 19
0.5χ ÷ 0.5 = 19 ÷ 0.5
χ = 38
1.5χ=1.5×38=57
答:一副乒乓球拍57元钱。
拓展应用
解析:设船在静水中每小时行χ千米。根据流水行船问题中的两个基本公式,则顺水的速度是χ+5,逆水速度是χ-5,根据“顺水时4小时行驶的路程=逆水时5小时行驶的路程”,进而列方程
解:设船在静水中每小时行χ千米。
( χ + 5 )× 4 = ( χ - 5 )× 5
4χ + 20 = 5χ - 25
4χ + 20 - 20 = 5χ - 25 - 20
4χ = 5χ - 45
χ = 45
答:这条船在静水中每小时行45千米.
2. 思路分析:根据两次分梨每个人分的个数不同,但梨的总数相等的关系列方程,一人一个多一个,意思是说:每人分一个还剩一个;一人两个少两个,意思是说每人分两个缺两个。设有χ个娃娃,则梨的个数可以表示为χ + 1和2χ - 2,梨的总数是相等的,列出方程
χ + 1 = 2χ - 2,求出χ的值就是求出娃娃的数量,最后求出梨的数量。
解:设有χ个娃娃
χ + 1 = 2χ - 2
χ = 3
χ + 1 = 3 + 1 = 4
答:有3个娃娃,4个梨。
信息窗3——等式的性质(二)和解形如aχ=b和χ÷a=b的方程
一、知识点解读
1.等式的性质(二)(理解识记)
知识点:等式两边同时乘或除以同一个数(O除外),等式仍然成立。
教学要求:教学时要充分运用学生在信息窗2中积累的探索等式性质的活动经验,通过天平平衡的原理放手让学生自主去尝试、去探索等式的性质(二)(在自主学习与合作交流中,如果学生没有想到同时除以0,教师可以自己向学生提出问题,简单讨论后,很快想到除法中除数不能为0,因而得出同时除以一个不为0的数的范围。)
2.运用等式的性质(二)解形如“aχ=b”和“χ÷a=b”的方程(掌握运用)
知识点:解法:先写解,接着方程左右两边同时除以(或乘)相同的数a,使方程左边只剩下χ,方程左右两边相等,再求χ的值,最后检验。
教学要求:让学生在理解了等式的性质(一)的基础上独立探究形如“aχ=b”和 “χ÷a=b”方程的解法,最后加以总结,并引导学生进行验算,培养学生自觉检验的意识,力求计算准确。
二、知识拓展
根据题目中的数量关系列方程解决生活中的实际问题。
根据数量关系列方程,也是通过寻找实际问题中数量之间的相等关系(等量关系),列出含有未知数的等式(方程)。这是解决实际问题的一种重要方法。首先看图弄清题意,分清已知与所求,找准各种数量之间的等量关系,再列方程并利用等式性质(二)正确解答。
常见的数量式、计算公式等都可以作为等量关系列方程。例如:
速度×时间=路程 工作效率×时间=工作总量 单价×数量=总价
(长+宽)×2=长方形的周长 长×宽=长方形的面积
边长×4=正方形的周长 边长×边长=正方形的面积
三、知识点训练
基础训练
在○里运算符号,在□里填数字。
1.5χ = 12 χ ÷ 3.2 = 17
解: 1.5χ ○ □ = 12 ○ □? 解: χ ÷ 3.2 ○ □ = 17 ○ □
χ = □? χ = □
2. 把方程与它对应的解用线连起来。
6χ = 0 χ = 2
χ ÷ 2 = 1 χ = 0.5
2χ = 1 χ = 0
3. 解方程。(带“★”写出检验过程)
2.5χ = 7.5 23χ = 138 ★ χ ÷ 4 = 25.5
能力提升
看图列方程并解答。
①
②
一块正方形菜地周长是64米,正方形的边长是多少米?
3. 黄豆长成豆芽后的质量是原来质量的8.5倍,现在需要豆芽493千克,需要黄豆多少千克?
拓展应用
三个连续自然数的和是54,求这三个数分别是多少?
2. 信业商厦为了方便残疾人的轮椅通行,做了一项关于建筑物高度的规定:每1米高的斜坡,至少需要12米的水平长度。商厦前面的空地长18米,那么此处斜坡最高是多少米?
训练题参考答案及解析
基础训练
1.5χ = 12 χ ÷ 3.2 = 17
解: 1.5χ ÷ 1.5 = 12 ÷ 1.5? 解: χ ÷ 3.2 × 3.2 = 17×3.2
χ = 8 χ = 54.4
2. 6χ = 0 χ = 2
χ ÷ 2 = 1 χ = 0.5
2χ = 1 χ = 0
2.5χ = 7.5 23χ = 138
解:2.5χ ÷ 2.5 = 7.5 ÷ 2.5 解:23χ ÷ 23 = 138 ÷ 23
x = 3 χ = 6
★ χ ÷ 4 = 25.5 检验: 方程左边 = χ ÷ 4
解:χ ÷ 4 × 4 = 25.5 × 4 = 102 ÷ 4
χ = 102 = 25.5
= 方程右边
所以,χ = 102是方程χ ÷ 4 = 25.5的解。
能力提升
1. 3y = 189 4χ = 24
解:3y ÷ 3 = 189 ÷ 3 解: 4χ ÷ 4 = 24 ÷ 4
y = 63 χ = 6
2. 解:设正方形菜地的边长是χ米。
4χ = 64
4χ ÷ 4 = 64 ÷ 4
χ = 16
答:正方形菜地的边长是16米。
3. 解:设需要黄豆χ千克。
8.5χ = 493
8.5χ ÷ 8.5 = 493 ÷ 8.5
χ = 58
答:需要黄豆58千克。
拓展应用
思路分析:三个连续自然数按从小到大的顺序排列,应该是后一个数比前一个数大1。可以设其中一个数为χ,另外两个数都可以用含有χ的式子表示,这样就可以根据三个数的和是54这一等量关系列方程。
方法一:
解:设这三个连续自然数中,最小的数为χ,则中间的数为χ+1,最大的数为χ+2。
χ + χ + 1 + χ + 2 = 54
χ = 17
χ + 1 = 17 + 1 = 18 χ + 2= 17 + 2 = 19
方法二:
解:设这三个连续自然数中,中间的数为χ,则最小的数为χ - 1,最大的数为χ + 1。
χ - 1 + χ + χ + 1 = 54
χ = 18
χ - 1 = 18 - 1 = 17 χ + 1 = 18 + 1 = 19
方法三:
解:设这三个连续自然数中,最大的数为χ,则中间的数为χ-1,最小的数为χ-2。
χ - 2 + χ - 1 + χ = 54
χ = 19
χ - 2 = 19 - 2 = 17 χ - 1 = 19 - 1 = 18
答:这三个连续自然数分别是17、18、19。
思路分析:1米高的斜坡至少需要12米的水平长度,由此得出题中的等量关系式是“12×斜坡高度=水平长度”。根据等量关系设此处斜坡最高是χ米,列方程求解。
解:设此处斜坡最高是χ米。
12χ = 18
12χ ÷ 12 = 18 ÷ 12
χ = 1.5
答:此处斜坡高度最高是1.5米。
信息窗4——列方程解决简单的实际问题
一、知识点解读
用形如“χ±a=b”和“aχ=b”的方程解决简单的实际问题(掌握运用)
知识点:列方程解决实际问题的步骤:
理解题意,找出已知数和未知数之间的等量关系
设未知数为χ
根据等量关系列方程
解所列的方程
检验并写出答语
教学要求:教学时,教师可以先引导学生分析要想解决问题需要弄清楚数量关系,让学生在独立思考的基础上展开讨论。学生可能出现两种情况:一种是用算术法解决,另一种是用方程解决。这时,教师要引导学生用列方程的方法解决问题,分析数量间的相等关系,写出等量关系式,再启发学生根据等量关系列出方程并解答。求出方程的解后,教师要启动教材中的问题“你会检验吗”,提醒学生把算得的结果代到原题当中去检验。
二、知识拓展
1.列方程解决问题时,要体现用方程解题的意义
例如:世界第一长河尼罗河全长约6671千米,比中国第一长河长江约长371千米,长江全长约多少千米?
错误示例:解:设长江全长约千米。
=6671-371
=6300
答:长江全长约6300千米。
正确解答:解:设长江全长约千米。
+ 371 = 6671
+ 371 - 371 = 6671 - 371
= 6300
答:长江全长约6300千米。
错解中计算并无错误,但没有体现用方程解题的意义,列出的方程中未知数并没有参与运算,本质上还是由已知量推出未知量,是一种算术法。列方程解决问题时,通常不能把未知数放在等号一边,而是用代替等量关系中的未知量直接列出方程。体验用方程解答应用题的优势,从而更加热爱数学,热爱生活。
2. 列方程解决实际问题时,方程的解的后面不写单位名称。
方程是一种等式,方程两边无论是数还是量都是相等的,因此两边的单位名称可同时约去。求方程的解的过程就成了数的恒等变形的过程,最后的结果是没有单位名称的,只需要在答语中把单位名称写清楚就行。
三、知识点训练
基础训练
看图写出等量关系式,并列出方程.
等量关系式:
方程:
2. 看图列方程并求出方程的解。
3. 小明去买商店衣服,优惠了38元,现价是75元,原价多少钱?(写出等量关系式并列方程解答)
等量关系式:
能力提升
天安门广场是世界上最大的首都中心广场,广场占地面积44万平方米,比俄罗斯红场多34.9万平方米。俄罗斯红场占地面积是多少万平方米?
树林中有杨树270棵,杨树的棵数是柳树的5倍。树林中杨树和柳树共有多少棵?
一块边长10米的正方形菜地与一块长12.5米的长方形菜地的面积相等,长方形菜地的宽是多少米?
拓展应用
远望巍巍塔七层,红红点点倍加增,共计三百八十一,试问顶层几盏灯?
7年前爸爸的岁数是小华的3倍,7年后是小华的2倍,小华今年多少岁?
训练题参考答案及解析
基础训练
1. 上衣的价钱+裙子的价钱=总价钱
χ + 46 = 112
2. 4χ = 60 120 + χ = 165
解:4χ ÷ 4 = 60 ÷ 4 解: 120 + χ - 120 = 165 - 120
χ = 15 χ = 45
原来的价钱 - 优惠的价钱 = 现在的价钱
解:设原价χ元。
χ - 38 = 75
χ - 38 + 38 = 75 + 38
χ = 113
答:原价113元。
能力提升
解:设俄罗斯红场占地面积是χ万平方米。
χ + 34.9 = 44
χ + 34.9 - 34.9 = 44 - 34.9
χ = 9.1
答:俄罗斯红场占地面积是9.1万平方米。
2. 解:设柳树有χ棵。
5χ = 270
χ = 54
270 + 54 = 324(棵)
答:树林中杨树和柳树共有324棵。
3. 解:设长方形菜地的宽是χ米.
12.5χ = 10 × 10
12.5χ ÷ 12.5 = 10 × 10 ÷ 12.5
χ = 8
答:长方形菜地的宽是8米。
拓展应用
思路分析:宝塔共7层,每层都挂着红灯,红灯的总数是381盏,红灯从顶层到底层“倍加增”,也就是每相邻的下一层红灯盏数都是上一层的2倍。可以设灯塔的顶层有χ盏灯,则第6层有2χ盏灯,第5层有4χ盏灯,依此类推,再根据红灯的总盏数列出方程。
解:设塔的顶层有χ盏灯。
χ + 2χ + 4χ + 8χ + 16χ + 32χ + 64χ = 381
127χ = 381
χ = 3
答:塔的顶层有3盏红灯。
2. 思路分析:本题直接设小华今年的年龄为χ岁,列方程、解方程都比较困难,可以设小华7年前是χ岁,则爸爸7年前为3χ岁。题中的等量关系比较隐蔽,就是:7年前爸爸的年龄 + 7 + 7 = 7年后爸爸的年龄,用含有χ的代数式表示出爸爸7年前、7年后的年龄,根据上面的等量关系,可以列出方程:
解:设小华7年前χ岁,则爸爸7年前为3χ岁。
3χ + 7 + 7 = 2(χ + 7 + 7)
3χ + 14 = 2χ + 28
? χ = 14
所以小华今年的年龄为:?14 + 7 = 21(岁)
答:小华今年21岁。
信息窗5——列方程解较复杂的应用题
一、知识点解读
1.学会解形式复杂的方程。(掌握运用)
知识点:学会解形式为aχ±b=c和aχ±bχ=c的方程。
教学要求:解形式为aχ±b=c和aχ±bχ=c的方程,先让学生主动去尝试解答,然后在交流研讨中会发现,解形式为aχ±b=c的方程,先运用了等式性质(一),又运用了等式性质(二)。解形式为aχ±bχ=c的方程,是运用四年级上册《用字母表示数》中的计算,如:7χ+8χ=15χ,把 aχ±bχ=c转化为(a±b)χ=c的简单方程。
2.会利用线段图理解数量关系列方程解决实际问题。(掌握运用)
知识点:学会看线段图理解数量关系列方程解决实际问题,在此基础上会画线段图。
教学要求:文字信息比较抽象,不直观,学生思维比较困难,教学时教师可以运用多媒体辅助教学,通过课件展示线段图的画法、动态演示数量关系的推理过程,呈现两种思路的对比分析,从而帮助学生学会分析、判断、推理数量关系,理清解题思路,用方程解决实际问题,感受画图解决问题的策略价值,从而让学生学会看图的方法。然后通过巩固练习,让学生体验运用画图策略解决问题的方便,并通过线段图说一说数量关系,提高学生分析问题、解决问题的能力。
二、知识拓展
船在江河里航行时,除了本身的前进速度外,还受到流水的推送或顶逆,在这种情况下计算船只的航行速度、时间和所行的路程,叫做流水行船问题。流水行船问题,是行程问题中的一种。
流水行船问题有以下两个基本公式,
顺水速度=船速+水速
逆水速度=船速-水速
船速是指船本身的速度,也就是静水中单位时间所走的路程。
水速,是指水在单位时间里流过的路程。
顺水速度和逆水速度分别指顺流航行时和逆流航行时船在单位时间里所行的路程。
三、知识点训练
基础训练
看图写出等量关系式,并列出方程。
等量关系式:
方程:
解方程:
5χ + 15 = 120 3.8χ - χ = 0.56 χ - 0.85χ = 3
写出题中的等量关系列出方程并求出方程的解。
一个水果店有苹果χ千克,香蕉122千克。香蕉的质量比苹果的3倍少28千克。
能力提升
解方程。
7χ + 3χ + 26 = 74 9χ + 8 = 102 - 13
一个长方形池塘的周长是300米。它的长是100米,宽是多少米?
一副乒乓球拍的价钱比一副羽毛球拍贵19元;乒乓球拍的价钱是羽毛球拍的1.5倍。一副乒乓球拍多少元钱?
拓展应用
一条轮船在两码头间航行,顺水航行需要4小时,逆水航行需5小时,水速是每小时5千米,这条船在静水中每小时行多少千米?
2. 一群娃娃去赶集,集上买了一堆梨,一人一个多一个,一人两个少两个,请问君子知道否,几个娃娃几个梨?
训练题参考答案及解析
基础知识
苹果的个数+梨的个数=总个数 χ + 2χ = 93
5χ + 15 = 120
解: 5χ+ 15 — 15 = 120 - 15
5χ = 105
χ = 21
3.8χ - χ = 0.56
解: 2.8χ = 0.56
2.8χ÷2.8 = 0.56 ÷ 2.8
χ = 0.2
χ - 0.85χ = 3
解: 0.15χ = 3
0.15χ ÷ 0.15 = 3 ÷ 0.15
χ = 20
3. 苹果重量×3-少的千克数=香蕉的重量
3χ - 28 = 122
解: 3χ - 28 + 28 = 122+28
3χ = 150
χ = 50
答:苹果有50千克。
能力提升
7χ + 3χ + 26 = 74
解: 10χ + 26 = 74
χ = 4.8
9χ + 8 = 102 - 13
解: 9χ + 8 = 89
χ = 9
2. 思路分析:已知长方形的周长和长求宽可以直接套用长方形周长公式:长方形的周长=(长+宽)×2
解:设宽是χ米。
(100 + χ )× 2 = 300
(100+χ)× 2 ÷ 2 = 300 ÷ 2
100 + χ = 150
100 + χ - 100 = 150 - 100
χ = 50
答:宽是50米。
3. 解:设一副羽毛球拍χ元,那么一副乒乓球拍1.5χ元。
1.5χ - χ = 19
0.5χ = 19
0.5χ ÷ 0.5 = 19 ÷ 0.5
χ = 38
1.5χ=1.5×38=57
答:一副乒乓球拍57元钱。
拓展应用
解析:设船在静水中每小时行χ千米。根据流水行船问题中的两个基本公式,则顺水的速度是χ+5,逆水速度是χ-5,根据“顺水时4小时行驶的路程=逆水时5小时行驶的路程”,进而列方程
解:设船在静水中每小时行χ千米。
( χ + 5 )× 4 = ( χ - 5 )× 5
4χ + 20 = 5χ - 25
4χ + 20 - 20 = 5χ - 25 - 20
4χ = 5χ - 45
χ = 45
答:这条船在静水中每小时行45千米.
2. 思路分析:根据两次分梨每个人分的个数不同,但梨的总数相等的关系列方程,一人一个多一个,意思是说:每人分一个还剩一个;一人两个少两个,意思是说每人分两个缺两个。设有χ个娃娃,则梨的个数可以表示为χ + 1和2χ - 2,梨的总数是相等的,列出方程
χ + 1 = 2χ - 2,求出χ的值就是求出娃娃的数量,最后求出梨的数量。
解:设有χ个娃娃
χ + 1 = 2χ - 2
χ = 3
χ + 1 = 3 + 1 = 4
答:有3个娃娃,4个梨。
