三年级下册数学一课一练-2.14长方形面积(一) 浙教版(含答案)
文档属性
| 名称 | 三年级下册数学一课一练-2.14长方形面积(一) 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 39.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-07-13 00:00:00 | ||
图片预览

文档简介
三年级下册数学一课一练-2.14长方形面积(一)
一、单选题
1.一块长方形菜地,长7米,宽9米,面积是(??? )平方米.
A.?63????????????????????????????????????????????B.?16????????????????????????????????????????????C.?32
2.如图,用8相同的长方形地砖刚好拼成一个宽为20cm的长方形图案(地砖间的缝隙忽略不计),则每块长方形地砖的面积是( ??)
A.?75cm2??????????????????????????????????B.?60cm2??????????????????????????????????C.?40cm2??????????????????????????????????D.?20cm2
3.一个长方形,它的长是宽的 倍,长是12厘米,面积是(?? )
A.?100平米厘米???????????????????B.?180平方厘米???????????????????C.?108平方厘米???????????????????D.?801平方厘米
4.长方形的长是10厘米,宽比长少5厘米,那么长方形的面积是(?? )
A.?50厘米??????????????????????????????????B.?150厘米??????????????????????????????????C.?50平方厘米
二、判断题
5.两个面积相等的长方形,周长也一定相等。
6.一个长方形的面积是216平方厘米,已知它的宽是9厘米,则长应该是24厘米。
三、填空题
7.长方体左、右每个面的长是________厘米,宽是________厘米,面积是________.
8.用6个边长为1厘米的正方形拼成一个长方形,拼成的长方形可能长是________厘米,宽是________厘米,面积是________平方厘米;也可能长是________厘米,宽是________厘米,面积是________平方厘米。
9.从一块正方形土地中,划出一块宽为1米的长方形土地(阴影部分),剩下的长方形土地面积是15.75平方米,划出去的长方形土地的面积是________.
四、解答题
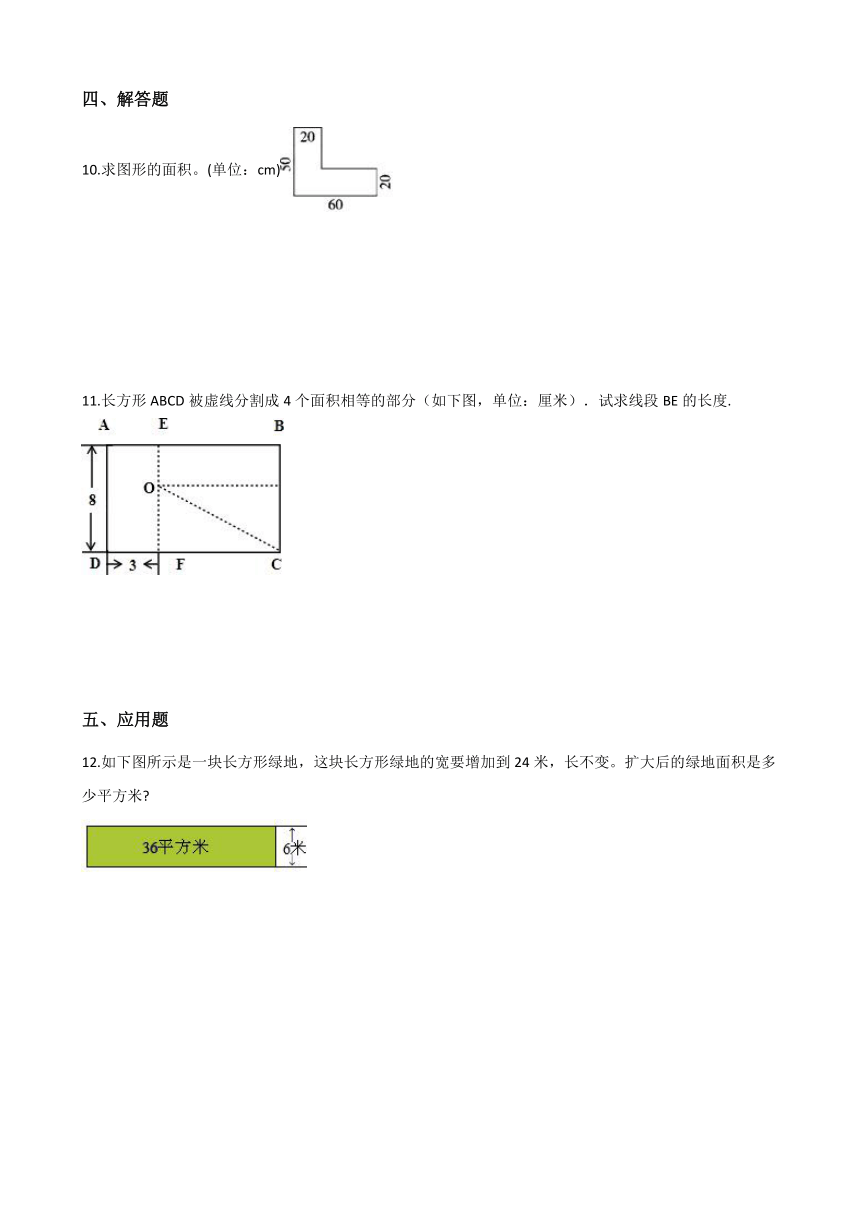
10.求图形的面积。(单位:cm)
11.长方形ABCD被虚线分割成4个面积相等的部分(如下图,单位:厘米).试求线段BE的长度.
五、应用题
12.如下图所示是一块长方形绿地,这块长方形绿地的宽要增加到24米,长不变。扩大后的绿地面积是多少平方米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】解:7×9=63(平方米) 故答案为:A。
【分析】长方形面积=长×宽,根据长方形面积公式计算面积即可。
2.【答案】 A
【解析】【解答】长方形的宽是:20÷4=5(cm), 长方形的长是:5×3=15(cm), 长方形的面积:15×5=75(cm2) 故答案为:A。 【分析】观察图可知,大长方形的宽相当于小长方形宽的4倍,用除法求出小长方形的宽,对比第一行与下面的图形可知,一个小长方形的长相当于小长方形宽的3倍,据此求出小长方形的长,最后用长方形的面积=长×宽,据此列式解答。
3.【答案】 C
【解析】【解答】解:12÷×12 =9×12 =108(平方厘米) 故答案为:C
【分析】用长除以即可求出宽,然后用长乘宽即可求出面积。
4.【答案】 C
【解析】【解答】长方形的长是10厘米已知,宽比长少5厘米, ,所以长是5厘米,根据长方形的面积计算公式有 (平方厘米)面积一定要用面积单位,所以后面应该跟的是平方厘米而不是厘米
【分析】此题考查同学们简单的计算能力以及对面积单位的理解,长度是厘米的面积单位是平方厘米,长度是米的面积单位是平方米,长度是分米的面积单位是平方分米
二、判断题
5.【答案】 错误
【解析】【解答】 例如:面积为8平方厘米的两个长方形,一个长方形的长和宽可以为8厘米和1厘米,则其周长为(8+1)×2=18(厘米); 另一个长方形的长和宽可以为4厘米和2厘米,则其周长为(4+2)×2=12(厘米); 所以说“两个面积相等的长方形,周长也一定相等”的说法是错误的。 故答案为:错误。
【分析】长方形的面积=长×宽,长方形的周长=(长+宽)×2,面积相等的两个长方形,周长不一定相等,据此举例解答。
6.【答案】正确
【解析】【解答】解:216÷9=24(厘米),原题计算正确。 故答案为:正确。
【分析】长方形面积=长×宽,用长方形的面积除以宽即可求出长,然后判断即可。
三、填空题
7.【答案】 4;3;12平方厘米
【解析】【解答】长:4厘米 ? 宽:3厘米 ? 面积: 3×4=12(平方厘米)
【分析】长方体相对的面对应的棱长相等,相对的面面积相等。
8.【答案】 6;1;6;3;2;6
【解析】【解答】 用6个边长为1厘米的正方形拼成一个长方形,拼成的长方形可能长是6厘米,宽是1厘米,面积是6平方厘米;也可能长是3厘米,宽是2厘米,面积是6平方厘米。 故答案为:6;1;6;3;2;6. 【分析】用6个边长为1厘米的正方形拼成一个长方形,可以拼成一排,长是6厘米,宽是1厘米,也可以拼成两排,每排3个,长是3厘米,宽是2厘米,要求长方形的面积,用长×宽=长方形的面积,据此列式解答.
9.【答案】 4.5平方米
【解析】【解答】 设正方形边长为x,则有 ?????? x(x-1)=15.75 ????????????? x2-x=15.75 x2-x+0.5×0.5=15.75+0.5×0.5 ????????? (x-0.5)2=16 ????????????? x-0.5=4 ??????????????????? x=4.5 阴影部分面积为4.5×1=4.5(平方米) 故答案为:4.5平方米。 【分析】此题主要考查了正方形、长方形面积的计算,设正方形边长为x,则有x(x-1)=15.75,据此求出x的值,然后用阴影部分的长×宽=阴影部分的面积,据此列式解答。
四、解答题
10.【答案】解:50×20+(60-20)×20 =1000+800 =1800(cm2)
【解析】【分析】可以把这个图形分成两个长方形来计算,左边长方形的长是50,宽是20,右边长方形的长是(60-20),宽是20。
11.【答案】解:长方形ADEF的面积:8×3=24(平方厘米), 长方形BCFE的面积:24×3=72(平方厘米), BE的长度:72÷8=9(厘米) 答:线段BE的长度是9厘米。
【解析】【分析】先计算长方形ADFE的面积,那么长方形BCFE的面积就是长方形ADEF面积的3倍,这样就能计算出长方形BCFE的面积;用这个面积除以BC的长度即可求出BE的面积。
五、应用题
12.【答案】解法一:360÷6=60(米) 60×24=1440(平方米) 答:扩大后的绿地面积是1440平方米。 解法二:24÷6=4 360×4=1440(平方米) 答:扩大后的绿地面积是1440平方米。
【解析】【分析】在解决问题时应整体考虑问题中已有的信息,这样解题的思路会更开阔。 已知原长方形绿地的面积是360平方米,宽是6米,根据“面积÷宽=长”求出长方形绿地的长是多少米,再用“长×宽=面积”求出扩大后的绿地面积;还可以根据长方形的长不变,宽扩大为原来的几倍,面积就扩大为原来的几倍来求出扩大后的绿地面积。
一、单选题
1.一块长方形菜地,长7米,宽9米,面积是(??? )平方米.
A.?63????????????????????????????????????????????B.?16????????????????????????????????????????????C.?32
2.如图,用8相同的长方形地砖刚好拼成一个宽为20cm的长方形图案(地砖间的缝隙忽略不计),则每块长方形地砖的面积是( ??)
A.?75cm2??????????????????????????????????B.?60cm2??????????????????????????????????C.?40cm2??????????????????????????????????D.?20cm2
3.一个长方形,它的长是宽的 倍,长是12厘米,面积是(?? )
A.?100平米厘米???????????????????B.?180平方厘米???????????????????C.?108平方厘米???????????????????D.?801平方厘米
4.长方形的长是10厘米,宽比长少5厘米,那么长方形的面积是(?? )
A.?50厘米??????????????????????????????????B.?150厘米??????????????????????????????????C.?50平方厘米
二、判断题
5.两个面积相等的长方形,周长也一定相等。
6.一个长方形的面积是216平方厘米,已知它的宽是9厘米,则长应该是24厘米。
三、填空题
7.长方体左、右每个面的长是________厘米,宽是________厘米,面积是________.
8.用6个边长为1厘米的正方形拼成一个长方形,拼成的长方形可能长是________厘米,宽是________厘米,面积是________平方厘米;也可能长是________厘米,宽是________厘米,面积是________平方厘米。
9.从一块正方形土地中,划出一块宽为1米的长方形土地(阴影部分),剩下的长方形土地面积是15.75平方米,划出去的长方形土地的面积是________.
四、解答题
10.求图形的面积。(单位:cm)
11.长方形ABCD被虚线分割成4个面积相等的部分(如下图,单位:厘米).试求线段BE的长度.
五、应用题
12.如下图所示是一块长方形绿地,这块长方形绿地的宽要增加到24米,长不变。扩大后的绿地面积是多少平方米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】解:7×9=63(平方米) 故答案为:A。
【分析】长方形面积=长×宽,根据长方形面积公式计算面积即可。
2.【答案】 A
【解析】【解答】长方形的宽是:20÷4=5(cm), 长方形的长是:5×3=15(cm), 长方形的面积:15×5=75(cm2) 故答案为:A。 【分析】观察图可知,大长方形的宽相当于小长方形宽的4倍,用除法求出小长方形的宽,对比第一行与下面的图形可知,一个小长方形的长相当于小长方形宽的3倍,据此求出小长方形的长,最后用长方形的面积=长×宽,据此列式解答。
3.【答案】 C
【解析】【解答】解:12÷×12 =9×12 =108(平方厘米) 故答案为:C
【分析】用长除以即可求出宽,然后用长乘宽即可求出面积。
4.【答案】 C
【解析】【解答】长方形的长是10厘米已知,宽比长少5厘米, ,所以长是5厘米,根据长方形的面积计算公式有 (平方厘米)面积一定要用面积单位,所以后面应该跟的是平方厘米而不是厘米
【分析】此题考查同学们简单的计算能力以及对面积单位的理解,长度是厘米的面积单位是平方厘米,长度是米的面积单位是平方米,长度是分米的面积单位是平方分米
二、判断题
5.【答案】 错误
【解析】【解答】 例如:面积为8平方厘米的两个长方形,一个长方形的长和宽可以为8厘米和1厘米,则其周长为(8+1)×2=18(厘米); 另一个长方形的长和宽可以为4厘米和2厘米,则其周长为(4+2)×2=12(厘米); 所以说“两个面积相等的长方形,周长也一定相等”的说法是错误的。 故答案为:错误。
【分析】长方形的面积=长×宽,长方形的周长=(长+宽)×2,面积相等的两个长方形,周长不一定相等,据此举例解答。
6.【答案】正确
【解析】【解答】解:216÷9=24(厘米),原题计算正确。 故答案为:正确。
【分析】长方形面积=长×宽,用长方形的面积除以宽即可求出长,然后判断即可。
三、填空题
7.【答案】 4;3;12平方厘米
【解析】【解答】长:4厘米 ? 宽:3厘米 ? 面积: 3×4=12(平方厘米)
【分析】长方体相对的面对应的棱长相等,相对的面面积相等。
8.【答案】 6;1;6;3;2;6
【解析】【解答】 用6个边长为1厘米的正方形拼成一个长方形,拼成的长方形可能长是6厘米,宽是1厘米,面积是6平方厘米;也可能长是3厘米,宽是2厘米,面积是6平方厘米。 故答案为:6;1;6;3;2;6. 【分析】用6个边长为1厘米的正方形拼成一个长方形,可以拼成一排,长是6厘米,宽是1厘米,也可以拼成两排,每排3个,长是3厘米,宽是2厘米,要求长方形的面积,用长×宽=长方形的面积,据此列式解答.
9.【答案】 4.5平方米
【解析】【解答】 设正方形边长为x,则有 ?????? x(x-1)=15.75 ????????????? x2-x=15.75 x2-x+0.5×0.5=15.75+0.5×0.5 ????????? (x-0.5)2=16 ????????????? x-0.5=4 ??????????????????? x=4.5 阴影部分面积为4.5×1=4.5(平方米) 故答案为:4.5平方米。 【分析】此题主要考查了正方形、长方形面积的计算,设正方形边长为x,则有x(x-1)=15.75,据此求出x的值,然后用阴影部分的长×宽=阴影部分的面积,据此列式解答。
四、解答题
10.【答案】解:50×20+(60-20)×20 =1000+800 =1800(cm2)
【解析】【分析】可以把这个图形分成两个长方形来计算,左边长方形的长是50,宽是20,右边长方形的长是(60-20),宽是20。
11.【答案】解:长方形ADEF的面积:8×3=24(平方厘米), 长方形BCFE的面积:24×3=72(平方厘米), BE的长度:72÷8=9(厘米) 答:线段BE的长度是9厘米。
【解析】【分析】先计算长方形ADFE的面积,那么长方形BCFE的面积就是长方形ADEF面积的3倍,这样就能计算出长方形BCFE的面积;用这个面积除以BC的长度即可求出BE的面积。
五、应用题
12.【答案】解法一:360÷6=60(米) 60×24=1440(平方米) 答:扩大后的绿地面积是1440平方米。 解法二:24÷6=4 360×4=1440(平方米) 答:扩大后的绿地面积是1440平方米。
【解析】【分析】在解决问题时应整体考虑问题中已有的信息,这样解题的思路会更开阔。 已知原长方形绿地的面积是360平方米,宽是6米,根据“面积÷宽=长”求出长方形绿地的长是多少米,再用“长×宽=面积”求出扩大后的绿地面积;还可以根据长方形的长不变,宽扩大为原来的几倍,面积就扩大为原来的几倍来求出扩大后的绿地面积。
同课章节目录
- 一 旅游中的数学问题
- 1.三位数除以整十数
- 2.单价、数量和总价
- 3.速度、时间和路程
- 4.工作效率、工作时间和工作总量
- 5.应用问题(一)
- 6.应用问题(二)
- 7.24时计时法
- 8.年、月、日
- 9.生活中的时间
- 二 篮球场上的数学问题
- 10.步测与目测
- 11.长方形周长(一)
- 12.长方形周长(二)
- 13.乘法分配律
- 14.长方形面积(一)
- 15.长方形面积(二)
- 16.面积单位的换算
- 17.两位数乘两位数
- 三 周末活动中的数学问题
- 18.数据的处理
- 四 丰收的果园
- 21.认识几分之一
- 22.认识几分之几(一)
- 23.分数的简单计算(一)
- 24.分数的简单计算(二)
- 25.认识几分之几(二)
- 26.应用问题(三)
- 27.认识小数(一)
- 28.认识小数(二)
- 五 总复习
