六年级上册数学试题-长方体和正方体的表面积和体积专项练习(无答案)
文档属性
| 名称 | 六年级上册数学试题-长方体和正方体的表面积和体积专项练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 425.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-25 08:44:29 | ||
图片预览

文档简介
长方体和正方体的表面积和体积专项练习
一、高减少或增加引起表面积的变化:
例题:一个长方体高减少3厘米后,表面积减少了72平方厘米,剩下的刚好是一个正方体,原来长方体的表面积是多少平方厘米?
试一试:
一个长方体,如果高增加2厘米,就成为一个正方体,这时表面积比原来增加了64平方厘米,原来的长方体的表面积是多少平方厘米?
二、拼接引起表面积的变化:
例题:
用两个长、宽、高分别是6分米、4分米、2分米的长方体拼成一个较大的长方体,这个长方体怎样拼表面积最大?怎样拼表面积最小?
2.用6个棱长是1厘米的小正方体拼成一个较大的长方体,拼成的长方体的表面积比原来减少了多少平方厘米?
试一试:
10包长、宽、高分别为8厘米、5厘米、2厘米的中华牌香烟,若用包装纸将他们打包成一个长方体,不计接头处,至少需要多少平方厘米的包装纸?
三、切割引起表面积的变化:
例题:将一个长10厘米、宽6厘米、高5厘米的长方体切成两个完全相同的小长方体,这两个小长方体的表面积总和比原来增加了多少平方厘米?
试一试:
(1)有一个长方体,若用三种不同的方法切成两个完全一样的长方体,它们的表面积分别增加30平方厘米、20平方厘米、12平方厘米。这个长方体的表面积是多少平方厘米?
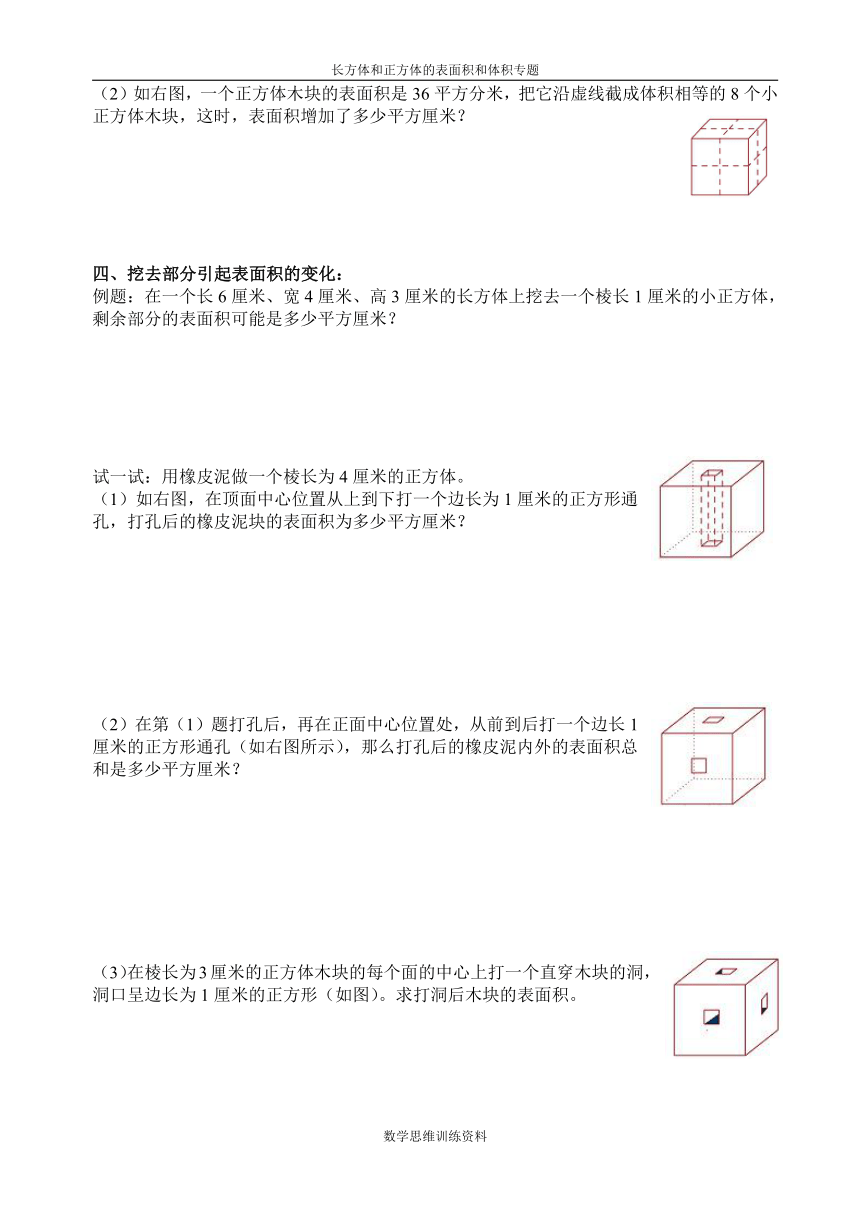
(2)如右图,一个正方体木块的表面积是36平方分米,把它沿虚线截成体积相等的8个小正方体木块,这时,表面积增加了多少平方厘米?
四、挖去部分引起表面积的变化:
例题:在一个长6厘米、宽4厘米、高3厘米的长方体上挖去一个棱长1厘米的小正方体,剩余部分的表面积可能是多少平方厘米?
试一试:用橡皮泥做一个棱长为4厘米的正方体。
(1)如右图,在顶面中心位置从上到下打一个边长为1厘米的正方形通孔,打孔后的橡皮泥块的表面积为多少平方厘米?
(2)在第(1)题打孔后,再在正面中心位置处,从前到后打一个边长1厘米的正方形通孔(如右图所示),那么打孔后的橡皮泥内外的表面积总和是多少平方厘米?
(3)在棱长为3厘米的正方体木块的每个面的中心上打一个直穿木块的洞,洞口呈边长为1厘米的正方形(如图)。求打洞后木块的表面积。
五、专项练习:
1.探索: 每个 都是棱长为1厘米的正方体,一个接一个排成一排。
个 数
1
2
3
4
…
图 形
…
表面积
(平方厘米)
…
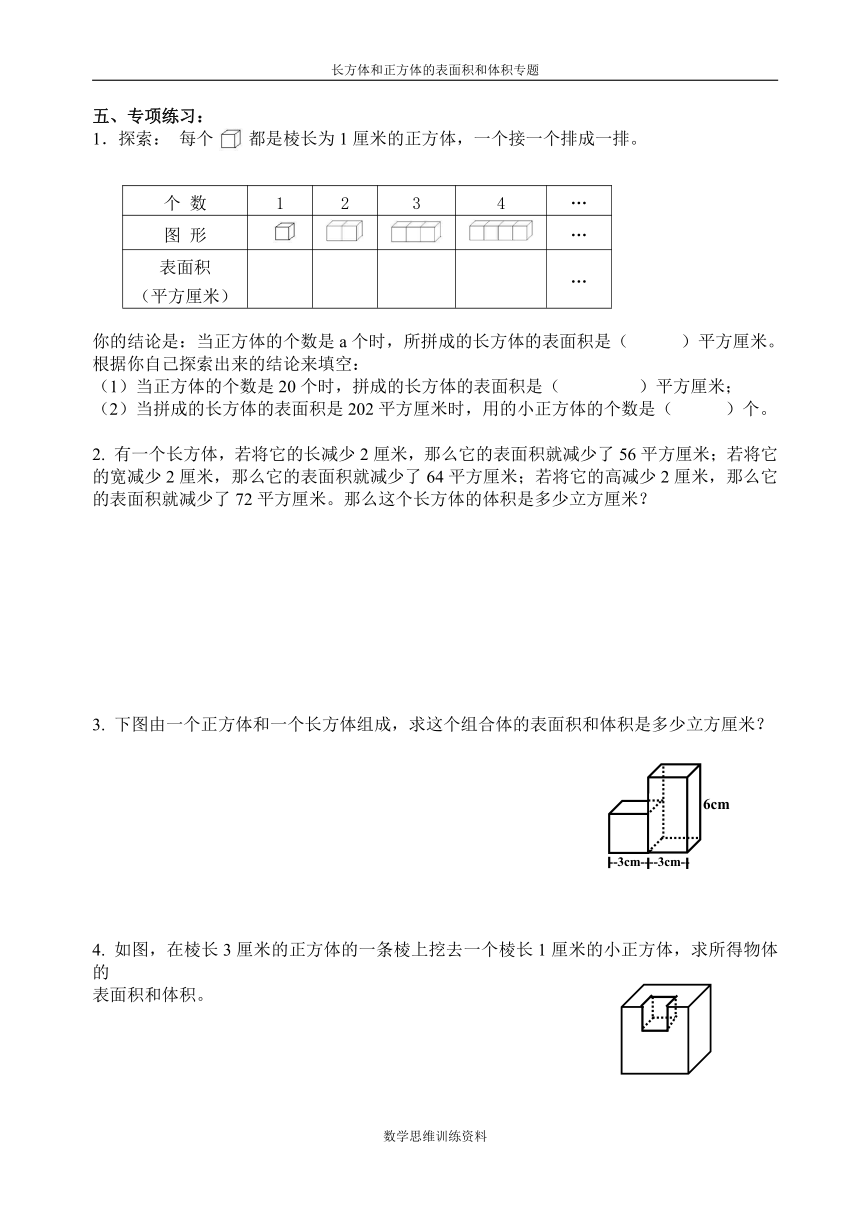
你的结论是:当正方体的个数是a个时,所拼成的长方体的表面积是( )平方厘米。
根据你自己探索出来的结论来填空:
(1)当正方体的个数是20个时,拼成的长方体的表面积是( )平方厘米;
(2)当拼成的长方体的表面积是202平方厘米时,用的小正方体的个数是( )个。
2. 有一个长方体,若将它的长减少2厘米,那么它的表面积就减少了56平方厘米;若将它的宽减少2厘米,那么它的表面积就减少了64平方厘米;若将它的高减少2厘米,那么它的表面积就减少了72平方厘米。那么这个长方体的体积是多少立方厘米?
3. 下图由一个正方体和一个长方体组成,求这个组合体的表面积和体积是多少立方厘米?
如图,在棱长3厘米的正方体的一条棱上挖去一个棱长1厘米的小正方体,求所得物体的
表面积和体积。
5. 30个棱长1厘米的正方体,在地面上摆成如右图的形状,然后把露出的表面涂成红色。那么,被涂成红色的面积是多少?
6. 有一块长40厘米,宽20厘米的铁皮,用它做一只深5厘米的无盖长方体铁盒(焊接处及铁皮的厚度忽略不计),你能想出几种设计方案?你认为哪种设计方案最好?为什么?
7. 如图所示,A的面积为30平方米,B的面积为20平方米,A比B高5米。现在要把A处的土堆到B处,使A、B两处同样高,这时B处比原来升高了多少米?
8.一个长方体,如果长减少2厘米,宽和高不变,则体积减少96立方厘米;如果宽增加3厘米,长和高不变,则体积增加99立方厘米;如果高增加2厘米,宽和长不变,则体积增加160立方厘米。问:原来这个长方体的表面积是多少?
9. 如图,在长、宽、高分别为10厘米、10厘米、6厘米的长方体容器中盛有深4厘米的水。若向容器中放入一个棱长为5厘米的正方体铁块,则水深多少厘米?
10. 水池A和B同为长3米、宽2米、深1.2米的长方体。1号阀门用来向A池注水,18分钟可将无水的A池注满;2号阀门用来从A池向B池放水,24分钟可将A池中满池水放入B池。若同时打开1号和2号阀门,那么当A池水深0.4米时,B池有多少立方米的水?
11. 一些棱长为1的小正方体码放成一个立体图形,从上向下看这个图形,如图(1),从正面看这个图形,如图(2)。在这个立体的体积最大时,将这些小正方体码放成一个底面积为4的长方体,则这个长方体的高是( )。
12. 如图,用若干个相同的小正方体摆成一个几何体,从上面、前面、左面看分别是图形①、②、③,则至少需要( )个。
13. (1)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点。如果大积木的棱长是2厘米,那么这个立体图形的表面积是多少平方厘米?
(2)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的三等分点。如果大积木的棱长是3厘米,那么这个立体图形的表面积是多少平方厘米?
14. 由四个完全相同的正方体堆积成如图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是( )。
15. 用8块棱长为1厘米的小正方体堆成一个立体。其俯视图如图所示,则共有( )种不同的堆法。(经旋转能重合的算一种堆法)
16. 如图所示,从长、宽、高分别为15厘米、5厘米、4厘米的长方体中切割走一块长、宽、高分别为y厘米、5厘米、x厘米的长方体(x和y为整数),余下部分的体积为120立方厘米,那么x为( )厘米,y为( )厘米。
17.一个长方体,棱长都是整厘米数,所有棱长之和是88厘米,则这个长方体总的侧面积最大是( )平方厘米。
18. 图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是( )。(填序号)
19. 某商场大厅的主楼梯如图所示,1楼到2楼共有15级台阶,每级台阶高16厘米,进深26厘米,已知楼梯宽3米,要在1楼到2楼的台阶上铺设红每平方米80元的地毯,则买地毯至少需要多少钱?
20. 将一个胶质的正方体扩大成另一个正方体,使新正方体的表面积是原正方体的4倍,则新正方体的棱长是原正方体的( )倍,体积是原正方体的( )倍。
21. 如图,三个相同的正方体堆成一个“品”字,每个正方体的六个面上都分别标有“小”“学”“希”“望”“杯”“赛”六个汉字,并且每个正方体上的汉字的排列顺序完全相同。问:正方体中,“希”“望”“杯”三个汉字的对面分别是哪个汉字?
22. 如图,用若干个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(包括底面积)是( )。
23.如图所示,一只蚂蚁从正方体的顶点A出发,沿正方体的棱爬到顶点B,要求行走的路线最短,那么蚂蚁有( )种不同的走法。
24. 若要组成一个表面积为52平方厘米的长方体,至少需要棱长1厘米的小正方体( )个。
一、高减少或增加引起表面积的变化:
例题:一个长方体高减少3厘米后,表面积减少了72平方厘米,剩下的刚好是一个正方体,原来长方体的表面积是多少平方厘米?
试一试:
一个长方体,如果高增加2厘米,就成为一个正方体,这时表面积比原来增加了64平方厘米,原来的长方体的表面积是多少平方厘米?
二、拼接引起表面积的变化:
例题:
用两个长、宽、高分别是6分米、4分米、2分米的长方体拼成一个较大的长方体,这个长方体怎样拼表面积最大?怎样拼表面积最小?
2.用6个棱长是1厘米的小正方体拼成一个较大的长方体,拼成的长方体的表面积比原来减少了多少平方厘米?
试一试:
10包长、宽、高分别为8厘米、5厘米、2厘米的中华牌香烟,若用包装纸将他们打包成一个长方体,不计接头处,至少需要多少平方厘米的包装纸?
三、切割引起表面积的变化:
例题:将一个长10厘米、宽6厘米、高5厘米的长方体切成两个完全相同的小长方体,这两个小长方体的表面积总和比原来增加了多少平方厘米?
试一试:
(1)有一个长方体,若用三种不同的方法切成两个完全一样的长方体,它们的表面积分别增加30平方厘米、20平方厘米、12平方厘米。这个长方体的表面积是多少平方厘米?
(2)如右图,一个正方体木块的表面积是36平方分米,把它沿虚线截成体积相等的8个小正方体木块,这时,表面积增加了多少平方厘米?
四、挖去部分引起表面积的变化:
例题:在一个长6厘米、宽4厘米、高3厘米的长方体上挖去一个棱长1厘米的小正方体,剩余部分的表面积可能是多少平方厘米?
试一试:用橡皮泥做一个棱长为4厘米的正方体。
(1)如右图,在顶面中心位置从上到下打一个边长为1厘米的正方形通孔,打孔后的橡皮泥块的表面积为多少平方厘米?
(2)在第(1)题打孔后,再在正面中心位置处,从前到后打一个边长1厘米的正方形通孔(如右图所示),那么打孔后的橡皮泥内外的表面积总和是多少平方厘米?
(3)在棱长为3厘米的正方体木块的每个面的中心上打一个直穿木块的洞,洞口呈边长为1厘米的正方形(如图)。求打洞后木块的表面积。
五、专项练习:
1.探索: 每个 都是棱长为1厘米的正方体,一个接一个排成一排。
个 数
1
2
3
4
…
图 形
…
表面积
(平方厘米)
…
你的结论是:当正方体的个数是a个时,所拼成的长方体的表面积是( )平方厘米。
根据你自己探索出来的结论来填空:
(1)当正方体的个数是20个时,拼成的长方体的表面积是( )平方厘米;
(2)当拼成的长方体的表面积是202平方厘米时,用的小正方体的个数是( )个。
2. 有一个长方体,若将它的长减少2厘米,那么它的表面积就减少了56平方厘米;若将它的宽减少2厘米,那么它的表面积就减少了64平方厘米;若将它的高减少2厘米,那么它的表面积就减少了72平方厘米。那么这个长方体的体积是多少立方厘米?
3. 下图由一个正方体和一个长方体组成,求这个组合体的表面积和体积是多少立方厘米?
如图,在棱长3厘米的正方体的一条棱上挖去一个棱长1厘米的小正方体,求所得物体的
表面积和体积。
5. 30个棱长1厘米的正方体,在地面上摆成如右图的形状,然后把露出的表面涂成红色。那么,被涂成红色的面积是多少?
6. 有一块长40厘米,宽20厘米的铁皮,用它做一只深5厘米的无盖长方体铁盒(焊接处及铁皮的厚度忽略不计),你能想出几种设计方案?你认为哪种设计方案最好?为什么?
7. 如图所示,A的面积为30平方米,B的面积为20平方米,A比B高5米。现在要把A处的土堆到B处,使A、B两处同样高,这时B处比原来升高了多少米?
8.一个长方体,如果长减少2厘米,宽和高不变,则体积减少96立方厘米;如果宽增加3厘米,长和高不变,则体积增加99立方厘米;如果高增加2厘米,宽和长不变,则体积增加160立方厘米。问:原来这个长方体的表面积是多少?
9. 如图,在长、宽、高分别为10厘米、10厘米、6厘米的长方体容器中盛有深4厘米的水。若向容器中放入一个棱长为5厘米的正方体铁块,则水深多少厘米?
10. 水池A和B同为长3米、宽2米、深1.2米的长方体。1号阀门用来向A池注水,18分钟可将无水的A池注满;2号阀门用来从A池向B池放水,24分钟可将A池中满池水放入B池。若同时打开1号和2号阀门,那么当A池水深0.4米时,B池有多少立方米的水?
11. 一些棱长为1的小正方体码放成一个立体图形,从上向下看这个图形,如图(1),从正面看这个图形,如图(2)。在这个立体的体积最大时,将这些小正方体码放成一个底面积为4的长方体,则这个长方体的高是( )。
12. 如图,用若干个相同的小正方体摆成一个几何体,从上面、前面、左面看分别是图形①、②、③,则至少需要( )个。
13. (1)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点。如果大积木的棱长是2厘米,那么这个立体图形的表面积是多少平方厘米?
(2)大小两个正方体积木粘在一起,构成如图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的三等分点。如果大积木的棱长是3厘米,那么这个立体图形的表面积是多少平方厘米?
14. 由四个完全相同的正方体堆积成如图所示的立体,则立体的表面上(包括底面)所有黑点的总数至少是( )。
15. 用8块棱长为1厘米的小正方体堆成一个立体。其俯视图如图所示,则共有( )种不同的堆法。(经旋转能重合的算一种堆法)
16. 如图所示,从长、宽、高分别为15厘米、5厘米、4厘米的长方体中切割走一块长、宽、高分别为y厘米、5厘米、x厘米的长方体(x和y为整数),余下部分的体积为120立方厘米,那么x为( )厘米,y为( )厘米。
17.一个长方体,棱长都是整厘米数,所有棱长之和是88厘米,则这个长方体总的侧面积最大是( )平方厘米。
18. 图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是( )。(填序号)
19. 某商场大厅的主楼梯如图所示,1楼到2楼共有15级台阶,每级台阶高16厘米,进深26厘米,已知楼梯宽3米,要在1楼到2楼的台阶上铺设红每平方米80元的地毯,则买地毯至少需要多少钱?
20. 将一个胶质的正方体扩大成另一个正方体,使新正方体的表面积是原正方体的4倍,则新正方体的棱长是原正方体的( )倍,体积是原正方体的( )倍。
21. 如图,三个相同的正方体堆成一个“品”字,每个正方体的六个面上都分别标有“小”“学”“希”“望”“杯”“赛”六个汉字,并且每个正方体上的汉字的排列顺序完全相同。问:正方体中,“希”“望”“杯”三个汉字的对面分别是哪个汉字?
22. 如图,用若干个棱长为1的小正方体堆成一个大的几何体,这个几何体的表面积(包括底面积)是( )。
23.如图所示,一只蚂蚁从正方体的顶点A出发,沿正方体的棱爬到顶点B,要求行走的路线最短,那么蚂蚁有( )种不同的走法。
24. 若要组成一个表面积为52平方厘米的长方体,至少需要棱长1厘米的小正方体( )个。
同课章节目录
